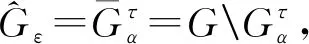小扭转映射的拟有效稳定性
李 宏 田
(中国刑事警察学院基础部,辽宁 沈阳 110854)
1 引言与主要结果
1977年,Nekhoroshev[1]建立了Hamilton系统的有效稳定性理论,与KAM稳定性[2-4]不同,他指出近可积Hamilton系统的全部轨道在指数长时间内不会发生显著变化,而KAM稳定性是说近可积系统的大部分轨道是永恒稳定的.然而Nekhoroshev提出的这种长时间稳定性依赖于陡性条件以及拟凸条件[1],这使得证明过程过于复杂.2015年,从福仲等[5]考虑用KAM型非退化条件来代替Nekhoroshev的陡性条件和拟凸条件,并且得到了一个弱于Nekhoroshev有效稳定性的结论,并将其定义为拟有效稳定性.本文继续了上述工作,考虑作用变量与角变量不同维情形的小扭转映射,并且在KAM型非退化条件下得到了高维小扭转映射的拟有效稳定性定理.
考虑实解析映射:Jt:Tn×G→Tn×Rm,
(1)
其中:Tn=Rn/Zn为n维环面;G⊂Rm是有界开集;fε(x,y)=εf(x,y)和gε(x,y)=εg(x,y)为关于x的1周期函数;ω,fε和gε在(G×Tn)+δ,δ>0上解析;ε>0为摄动参数;t∈[0,1]为小扭转参数.
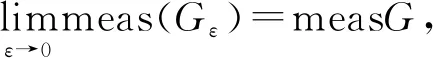
则称映射(1)具有拟有效稳定性.
定理1.1 如果实解析映射(1)满足如下条件:
(A1) 存在M>0,使得
(2)
(A2) Jt在G×Tn上具有相交性;
(A3) 频率ω(y)具有非退化性,
则映射(1)具有拟有效稳定性.
2 近不变环面性质

定理2.1 若映射(1)满足(A1)—(A2),对于任意给定的y0∈G频率ω(y0)满足Diophanto条件:
(A3*)
|e2πi〈k,tω(y0)〉-1|≥tα|k|-τ,∀k∈Zn0<|k|≤L(κ),t∈(0,1],
其中:α,τ>0;
κ (3) 为常数;L(κ)为截断的阶数.则存在一个仅依赖于M,n,α,K1,τ,δ以及κ的常数ε0>0,使得∀ε∈[0,ε0],都存在(Tn×{y∈G||y|≤K1})+δ上的坐标变换E: (4) 以及Tn×{y∈G||y|≤K1}上的近恒等变换(x,y)=Tj(X,Y), j=1,…,N(κ),使复合变换E∘T1∘…∘TN(κ)将(1)式化为 (5) 其中 其中:(x(r),y(r))=Jr(x,y);c0,c1,c2>0为常数. (6) 这里 (7) (8) 其中(x,y)∈(Tn×{y∈G||y|≤K1})+δ.显然f0,g0实解析,并且满足 max{‖f0‖+‖g0‖,|ω(y0)|} (9) (10) 且 (11) 做变换Tj:(X,Y)→(x,y), (12) (13) (14) 记 (15) 由差分方程有 vj(x+tω(y0),y)-vj(x,y)=t[gj]L(x,y), (16) (17) 令 由文献[5],在Dj+1上有如下估计: (18) (19) 这里Ω*=ΩN,f*=fN,g*=gN. 由文献[5],有 (20) 从而,若κ充分小, |y(r)-y|≤|y-Y|+|y(r)-Y(r)|+|Y(r)-Y|≤c2κ. 并且 取τ=n2+n.记 类似文献[6],有 对任意y0∈G*,取 α(y0)=max{α|0<α<1,|e2πi〈k,tω(y0)〉-1|≥αt|k|-τ,∀k,0≠k∈Zn}, ε(y0)=α(y0)2(τ+n+4),Dε(y0)=D(y0,ε). 对ε∈(0,ε0],若0<ε≤ε(y0),由定理2.1,对任意的(X,Y)∈Dε(y0)×Tn,只要r≤c0exp(ηε-β),则 |y(r)-y|≤ηεγ, 令 (21) 至此完成了定理1.1的证明.
2.1 标准化
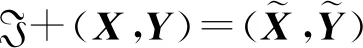

2.2 KAM迭代






3 小扭转映射的拟有效稳定性