基于小波阈值去噪与t-SNE的船舶柴油机故障识别
尚前明,沈 栋,边祥瑞
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
柴油机作为内燃机的一种,在船舶上的应用十分广泛。作为船上重要的动力来源,人们对其工作的稳定性有着很高的要求。因为设备不可能一直处于正常的工作状态,会出现各种类型的故障,所以对设备参数的监测与安全检修、维护保养也是必要的。根据船舶柴油机常见的故障类型,其对应的故障诊断技术有很多,但基本以热工参数[1,2]为主要诊断依据,其实船舶柴油机的机械振动信号中也蕴含很多的运行状态信息,基于振动信号进行故障的分析与处理[3,4]有着很大的现实意义。
然而在处理振动信号时,由于原始信号中存在的噪声信号容易对诊断结果产生一定的影响,故必须对其进行降噪。本文将采用小波阈值降噪的方法对振动信号进行降噪处理,然后利用不同工况下相同频带上振动能量不同的特点,将其作为特征向量,并结合部分时频域的统计参数设计成一个特征集,使用t-SNE对特征进行降维处理,除去部分冗余的相关性小的特征量。最后使用支持向量机进行故障的诊断,求出识别率。经仿真实验验证,该诊断方案具有较高的识别准确率。
1 基本原理
1.1 小波阈值去噪
船舶柴油机在运转时,其振动信号具有噪声干扰大、非线性、非平稳的特点,所以在对其进行特征提取之前,需要对原始数据进行降噪处理。而小波变换有低熵性、时频分析优良、多解析率和去相关性等特点,所以本文使用小波分析进行振动信号的非线性降噪。由于小波变换的去相关性特性,在经过小波变换后,信号之间就变得没有关联。也正是这种特性使得有效信号在经过小波变换后,能根据小波系数的不同区分出噪声和能量的位置,从而再进行重构,获得的新信号就是去噪后的信号。根据选择的阈值不同,小波阈值去噪可分为硬阈值去噪和软阈值去噪。小波阈值去噪步骤具体如下。
1)小波分解。选择合适的小波基函数,确定需要分解的层次,然后对原始信号进行相应层次的小波分解,得到各层的小波系数。
2)阈值处理。用合适的阈值处理方式对分解后所得的高频系数进行阈值处理。
3)小波重构。根据小波分解最后一层的低频系数和经过修改的高频系数,进行小波重构,得到降噪后的信号。
在小波变换后需要对所得的小波系数进行阈值处理,一般的阈值处理方式分为硬阈值函数处理和软阈值函数处理。
(1)硬阈值函数:当小波系数w的绝对值小于给定阈值λ时,直接令小波系数为0;大于阈值时,则保持不变:
(1)
(2)软阈值函数:当小波系数w的绝对值小于给定阈值λ时,直接令小波系数为0;大于阈值时,令其减去阈值:
(2)
1.2 t-SNE流形学习算法
t-SNE是Hinton等[5]基于SNE算法提出的一种新算法。它的核心是引入自由度为1的t分布函数代替高斯分布,构建高维空间数据样本的概率分布,并在低维子空间构建对应样本的概率分布,采用 KL 散度(相对熵)来衡量高低维空间的概率分布的相似程度,从而实现降维的效果。t-SNE算法降维的原理如下:在高维空间中,假定有N个数据样本x,xi、yj为高维空间中任意2点,且xi的取值服从以xi为中心、方差为δi的高斯分布,同样xj服从以xj为中心、方差为δj的高斯分布。首先计算xi和xj之间的条件概率pj|i和pi|j,进一步得到联合概率pij。然后求取分布在低维空间中的yi和yj之间的联合概率qij,使用KL散度来构造目标函数,使用梯度下降法来寻找高维样本映射到低空间表达的最优解。
1.3 支持向量机
支持向量机[6]是1995年Cortes和Vapik提出的一种机器学习算法。其核心原理是利用映射函数将原始数据映射到高维空间,在高维空间内寻求一个分离线或分离面使样本点间距离最大,从而达到样本的分离[7]。SVM学习基本思想是求解一个分离超平面,使其能正确划分训练数据集且保证几何间隔最大。作为一种二分类模型,支持向量机在具体使用过程中会结合数据样本的特点选择对应的核函数K(x,x′)和适当的惩罚参数C,用以构造目标函数并对其求解最优问题。为获得最佳的核函数和惩罚参数,本文结合遗传算法进行寻优。遗传算法是模拟自然界生物遗传的寻优算法,在进行交叉验证方法条件下的准确率达到最高时,当下一组惩罚参数C和核函数K即为最优解,进行对测试集的验证。优化后的GA-SVM算法流程图见图1。
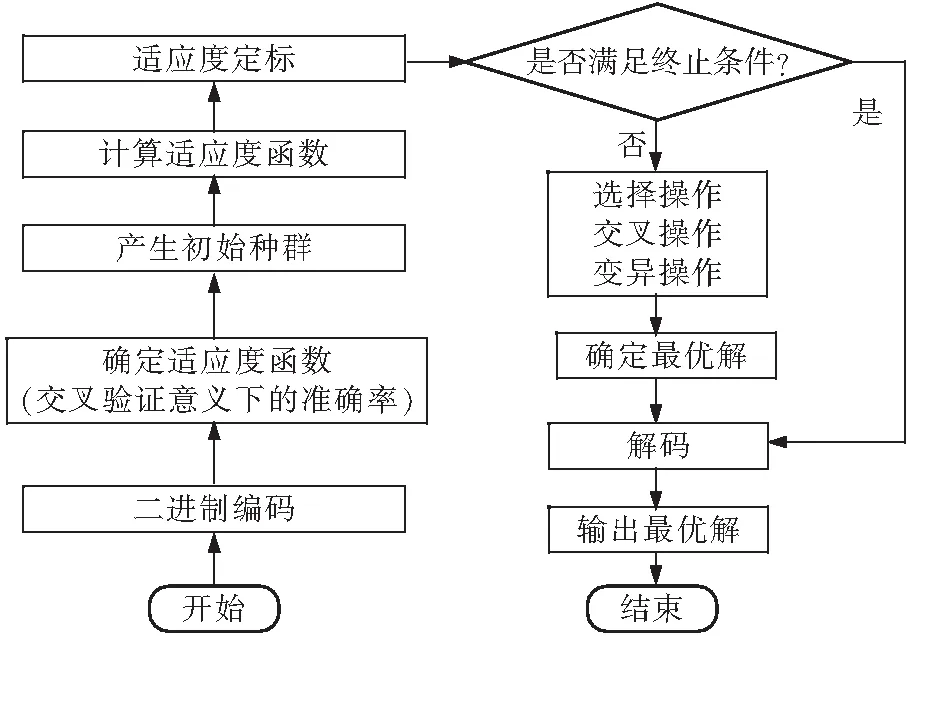
图1 优化后的GA-SVM算法流程图
2 故障诊断方法设计
由于不同的小波阈值去噪方法有不同的分析结果,本文提出一种将小波阈值去噪和t-SNE结合的故障诊断方法,最终选取出可以使用SVM判别故障类别的敏感数据集。具体步骤如下:①对振动信号进行小波分解,获得各尺度的小波系数,对高频的小波系数分别进行硬阈值处理和软阈值处理;②针对2种阈值处理方式,计算信号的信噪比(SNR)和均方根误差(RMSE);③对比去噪信号图像与原始信号图像的相似度,以及SNR和RMSE的大小,找出最合适的小波阈值处理方式;④利用t-SNE对去噪后的特征数据进行降维,去除冗余不相关特征;⑤将降维后的低维特征数据分为训练集与测试集,将训练集输入到GA-SVM中进行训练;⑥用训练好的GA-SVM对测试集进行分类,根据输出结果确定故障类型并计算识别准确率。
3 应用与分析
为了验证“故障诊断方法”中设计方法的有效性,利用实验对其进行验证分析。本文实验数据是从实验台架采集得到的,该实验台架上的是YXR6110IZLD型柴油机,通过在1#缸的缸盖上设置传感器以获得振动信号。对该柴油机分别进行了3种不同故障的模拟实验,在40 kHz的采样频率和1 500 r/min的额定转速下进行数据采集,并获得实验数据。故障类型及其模拟方式如表 1所示。

表1 故障类型及其模拟方式
3.1 小波阈值去噪与特征提取
对4种不同工况的样本数据进行分析,将小波阈值去噪方法应用于样本数据。选取本实验柴油机一个工作循环中所采集的振动信号进行分析,取sym6为小波基函数,小波分解的层数为4。对样本数据进行小波变换之后,使用不同的阈值处理修改高频的小波系数,再进行信号重构获得降噪后的信号,同时对比硬阈值处理和软阈值处理方式对结果的影响,得到不同工况下软、硬阀值处理后的SNR与RMSE对比如表2所示。
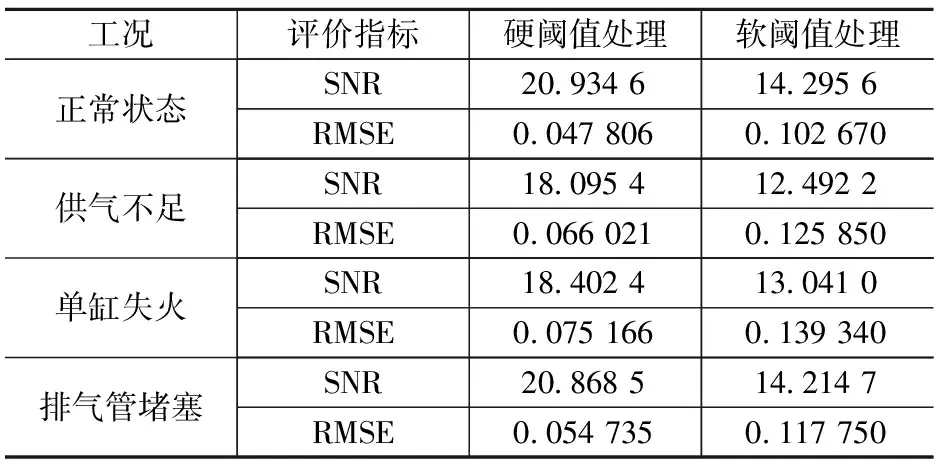
表2 不同工况下软、硬阈值处理后的SNR与RMSE对比
由表2知,正常状态、供气不足、单缸失火和排气管堵塞这4种工况下,信噪比的大小排列为硬阈值>软阈值,而均方根误差刚好相反。同时,硬阈值去噪处理后的信号与原始信号更加接近,保留的细节更多,由此得出在该实验案例中,硬阈值处理方式优于软阈值处理方式。
硬阈值处理后的信号进行小波系统重构,根据信号在16个频段内的能量谱作出小波能量谱的特征向量图,小波能量谱特征向量图如图2所示。实验所测的4种工况的能量谱特征均值主要分布在频带5~16,且不同工况的能量分布不同,适合作为特征向量以区分不同的工况。
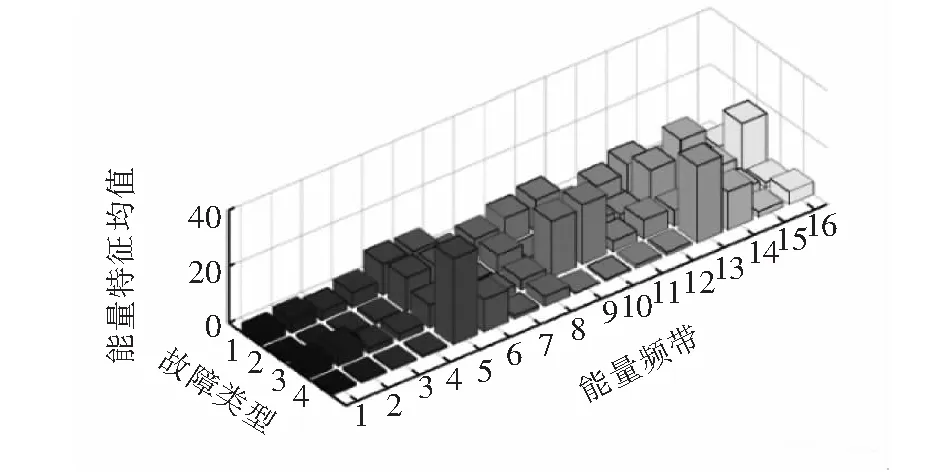
图2 小波能量谱特征向量图
3.2 特征降维与诊断结果
提取缸盖上振动信号的均方根值、脉冲、波形、裕度、峰值和峭度等统计指标,与归一化后的能量谱特征向量结合,形成新的特征向量。为减少后面GA-SVM的计算,提高诊断的效率,使用t-SNE进行降维,t-SNE和PCA的降维结果分别见图3、图4。如图所示,t-SNE能将不同工况的样本数据清晰地分开,降维效果较PCA好。
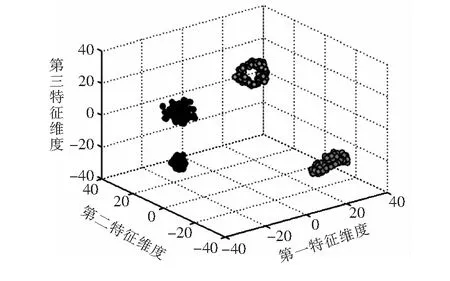
图3 t-SNE降维结果
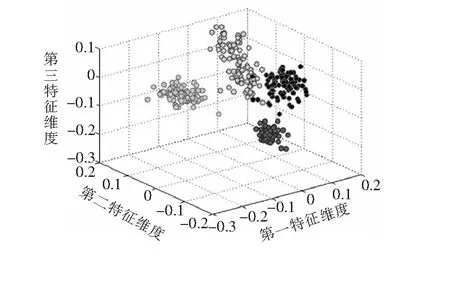
图4 PCA降维结果
取使用t-SNE降维后的4种工况的特征数据用训练好的GA-SVM进行分类,每种工况的20个样本的测试集进行故障分类验证。GA-SVM故障分类结果显示,正常状态、供气不足故障、单缸失火故障和排气管堵塞故障的故障识别准确率分别为100%、95%、100%和90%,均在90%以上。
4 结束语
针对船舶柴油机振动信号非线性和非平稳性的特点,本文提出一种基于小波分析和t-SNE算法结合的故障诊断方法,利用小波分解并进行阈值去噪,使用能量谱和一些时频域统计量作为故障的特征向量,并对其进行t-SNE降维,最后使用GA-SVM进行故障的诊断。仿真实验表明,本文提出的诊断方法具有较高的准确率,能有效地使用振动信号对船舶柴油机进行故障诊断。

