LNG接收站储罐温度场及其参数优化研究

李昭辉，朱汉华，朱志鹏，门 皓，张 梦

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

液化天然气(LNG)一般储存在常压下，温度为111 K，利于储存和运输。液化天然气比同质量的其他气体体积小很多，需要绝热技术,来防止或减小液体的蒸发。如不采取绝热技术会造成大量液化气体的蒸发[1]，甚至发生事故[2]。在国内，李兆慈[3]对储罐进行了三维温度场分析，分别是环境温度、风速、液位高度对其温度场的影响。罗义英[4]研究了LNG储罐底部泡沫玻璃的厚度与蒸发率的关系曲线。范嘉堃[5]通过现场实测储罐表面温度分布情况，发现与理论分析结果有偏差。在国外，Dong[6]对30 000 m3液化天然气储罐进行整体温度场和热应力分布的分析，Zhao利用正交脊波变换和有限元方法相结合，来研究液化天然气储罐液体分层的温度场分析。本文将采用理论分析和数值仿真相结合的方法，对LNG接收站储罐温度场进行模拟分析，揭示了储罐传热特征，并对储罐的设计参数进行优化，提高储罐的保冷性。

1 LNG储罐散热分析

1.1 LNG储罐的结构与相关参数

本文研究对象是罐容积约为8×104m3的LNG全容式双壁金属罐，储罐内直径约为58 m、外直径约为60.0 m、外罐高约36.5 m、内罐高约34.3 m。内壁与外壁之间采用堆积绝热的方式，外界环境温度为296 K，LNG的密度为436.3 kg/m3，LNG的汽化潜热为510 kJ/kg，8×104m3LNG储罐结构示意图见图1，储罐绝热材料参数见表1。

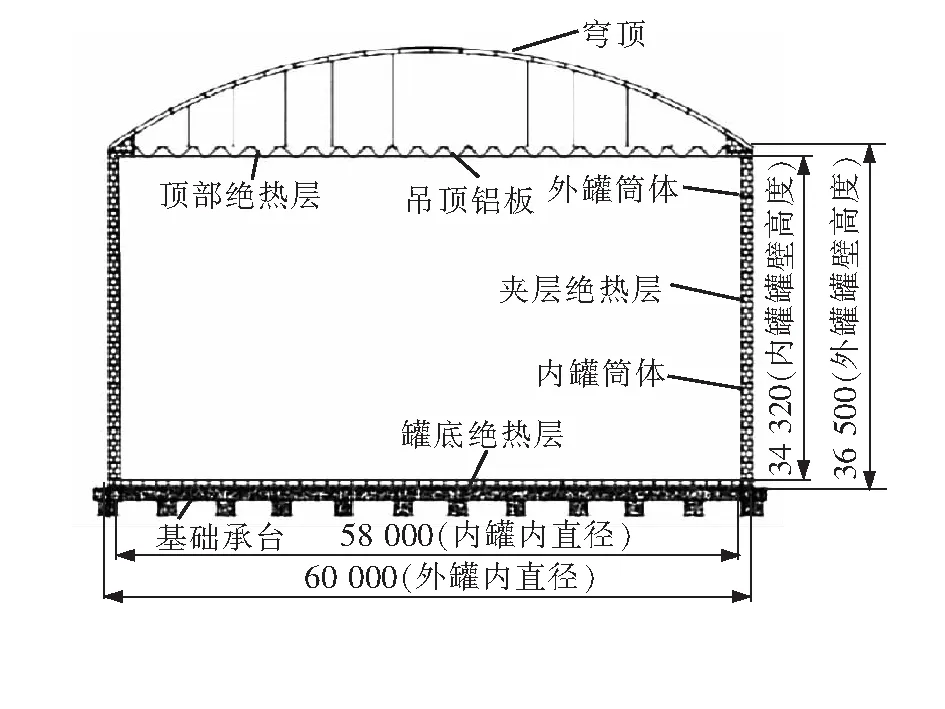
图1 8×104 m3LNG储罐结构示意图

表1 储罐绝热材料参数

1.2 漏热理论分析

1)罐顶漏热量计算。罐顶的漏热主要是由3部分组成，穹顶外壁向内壁的热传导Q11，由内罐穹顶向吊顶上表面的热辐射Q12，吊顶上表面向内罐顶的热传导Q13；ε1为穹顶下表面的发射率，ε2为吊顶上表面的发射率；A1为穹顶下表面的面积，A2为吊顶上表面的面积；X1,2为吊顶上表面对穹顶下表面的角系数；Tw为外界环境温度，T1为穹顶下表面温度，T2为吊顶上表面温度，Tn为储罐内部LNG液体温度；σb为黑体辐射常数，σb=5.67×10-8W/(m2·K4)；λ1为穹顶低碳钢的导热系数，λ2为玻璃纤维的导热系数，λ3为铝箔的导热系数；σ1为穹顶的厚度，σ2为吊顶玻璃纤维层的厚度，σ3为铝箔的厚度。

穹顶热阻R1,1和外界环境向穹顶的热传导Q11分别为：

(1)

(2)

穹顶向吊顶上表面进行热辐射的热阻R1,2和穹顶向吊顶上表面的热辐射Q12分别为:

(3)

(4)

吊顶热阻R1,3和通过吊顶的热传导Q13为：

(5)

(6)

根据传热学原理，Q11=Q12=Q13：

(7)

2)罐壁漏热量计算。外界热量透过储罐罐壁传入罐内的传热过程可以看作多层圆筒壁的稳态导热。储罐内罐的半径为r1，到9%Ni钢板的半径为r2，到弹性毡的半径为r3，到珍珠岩的半径为r4，到外罐壁钢板的半径为r5;λ4为9%Ni钢板的导热系数，λ5为弹性毡的导热系数，λ6为珍珠岩的导热系数，λ7为16MnDR钢板的导热系数。

罐壁材料的导热热阻R2为：

(8)

外界环境通过储罐罐壁向内罐传递的热量Q2为：

(9)

3)罐底漏热量计算。外界热量透过储罐底部传入罐内的传热过程可看作是多层平壁的稳态导热。λ8为干沙的导热系数，λ9为泡沫玻璃砖的导热系数，λ10为混凝土的导热系数，σ8为内罐底9%钢板的厚度，σ9为罐底干沙的厚度，σ10为罐底泡沫玻璃砖的厚度，σ11为罐底混凝土的厚度，σ12为外罐底板的厚度。

罐底材料的导热热阻R3为：

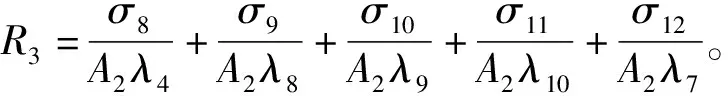
(10)

外界环境通过储罐罐底向储罐内部传递的热量Q3为：

(11)

1.3 有限元分析的边界条件及假设

由于LNG全容式双壁金属罐结构复杂，为了方便建立模型，现对仿真过程进行如下的假设：①储罐所有材料的导热系数不随温度变化而变化；②罐体内LNG处于饱和状态，即罐内LNG的温度处处相等，即为111 K。

运用有限元软件计算罐体温度场可以分为3步：建立几何模型并进行网格划分；施加边界条件并求解；通过后处理，输出结果，包括温度分布图、热流密度图等。

取吊顶单位长度横截面进行分析计算，分析单元取plane35单元，对吊顶截面模型进行网格划分，对吊顶下表面施加载荷，即Tn=111 K，罐内液体对罐体的对流换热系数为103.2 W/(m2·K)；对吊顶上表面施加载荷，即T2=292.98 K，气体对流换热系数取为5 W/(m2·K)。

由于储罐的轴对称性，取储罐罐壁的1/360(1°)进行分析计算，分析单元选取plane55单元，对外罐壁钢板外表面施加载荷，即Tw=296 K，对内罐壁9%Ni钢板施加载荷，即Tn=111 K，外罐壁与空气对流换热系数取13.805 W/(m2·K)。

取罐底的单位长度横截面进行分析计算，分析单元选取plane35单元，对内罐罐底板9%Ni钢上层施加载荷，即Tn=111K，罐底外壁钢板下层施加载荷，即Tw=296 K，储罐底部与空气的对流换热系数为22.10 W/(m2·K)。

2 计算模型与验证

2.1 计算模型验证

利用ANSYS中的APDL方法对储罐漏热进行仿真，储罐各部分的漏热分布如表2所示。

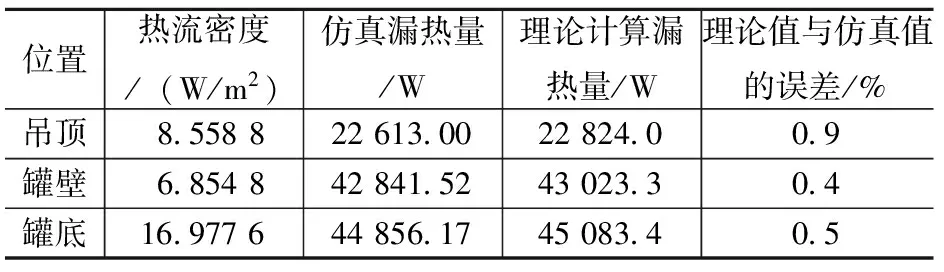
表2 储罐各部分的漏热分布

根据前文理论分析结果计算可知，吊顶的理论计算漏热量为22 824.0 W；由仿真结果分析可知，吊顶的热流密度值为8.558 8 W/m2，则吊顶的仿真漏热量为22 613.00 W，与理论计算值的误差为0.9%，说明计算结果较为准确。

根据前文理论分析结果计算可知，罐壁的理论计算漏热量为43 023.3 W；由仿真结果分析可知，罐壁的热流密度为6.854 8 W/m2，则罐壁的仿真漏热量为42 841.52 W，与理论计算值的误差为0.4%，说明计算结果较为准确。

根据前文理论分析结果计算可知，罐底的理论计算漏热量为45 083.4 W；由仿真结果分析可知，罐底的热流密度为16.977 6 W/m2，则罐底的仿真漏热量为44 856.17 W，与理论计算值的误差为0.5%，说明计算结果较为准确。

2.2 计算结果验证

根据在某地LNG接收站的调研，测出了1天内每小时实测液面高度的数据，根据液位高度的变化数据，可以计算出1天之内LNG的蒸发量，根据蒸发量可计算出1天之内LNG的漏热量，并与现在的数值模拟分析得出的漏热量进行对比。图2为数值模拟结果与现场勘测数据对比验证，发现结果基本吻合。

图2 数值模拟结果与现场勘测数据对比验证

3 参数优化

3.1 设计参数下漏热量

根据理论计算和数值模拟的计算结果，储罐罐底的漏热量约占储罐总体漏热量的40.7%，而储罐罐底的漏热量与罐底的保冷层(泡沫玻璃砖)的厚度具有显著的关系。为减少储罐整体的漏热量，研究罐底的保冷层参数具有显著的意义。

罐内储存的介质为111 K的液化天然气，在正常情况下，罐内的液体处于静止状态，根据传热学的公式可知，内罐底部与天然气的对流换热系数hn=103.25 W/(m2·K)，外罐底与外界空气的对流换热系数hd=22.10 W/(m2·K)。

根据设计条件，LNG储罐底部单位面积的漏热量Q：

(12)

得出Q=16.98 W，与数值模拟的结果相近。

3.2 储罐罐底最大允许漏热量

由本地气象局提供的信息可知，某地LNG接收站的夏季温度最高为308 K，相对湿度η=80%，则露点温度Td=304 K，外界环境温度Tw=296 K，根据《工业设备及管道绝热工程设计规范》可知，那么Tw-Td=-8.0 K<-4.5 K，LNG 储罐的单位面积最大允许漏热量Qmax：

Qmax=-(Tw-Td)hd。

(13)

得出Qmax=176.8 W。当储罐在设计条件下，即罐底的保冷层(泡沫玻璃砖)的厚度为520 mm时，罐底单位面积的漏热量为16.98 W，计算可得，罐底单位面积的漏热占单位面积最大允许漏热量的9.6%。

3.3 LNG储罐底部参数优化

使用有限元方法进行传热分析，由传热学公式可知，由于罐底漏热量与泡沫玻璃砖的厚度呈连续函数关系，假设泡沫玻璃砖的厚度为θ，分析θ=0、100、200、300、400、500、600、700、800、900、1 000、1 100、1 200、1 300、1 400、1 500、1 600(单位mm)，这17种工况下罐底的热流密度，进而求出相对应罐底的漏热量。泡沫玻璃砖厚度与热流密度和漏热量的关系见表3。

表3 泡沫玻璃砖厚度与热流密度和漏热量的关系

根据表3做出罐底漏热量与泡沫玻璃砖厚度的关系曲线如图3所示，可得出以下结论。

图3 罐底漏热量与泡沫玻璃砖厚度的关系曲线

1)当罐底不加保冷层时，即θ=0,罐底的漏热量占最大允许漏热量的367.8%；当θ=100 mm，罐底的漏热量占最大允许漏热量的45%，说明加入保冷层能有效地阻止储罐的漏热。

2)当罐底保冷层厚度为设计值θ=520 mm时，罐底的漏热量占最大允许漏热量的9.6%，罐底的漏热量占储罐整体漏热量的41%，说明此厚度下罐底的保冷效果已经非常显著。

3)当继续增大保冷层厚度，θ=1 200 mm时，罐底的漏热量占最大允许漏热量的4.2%，罐底的漏热量占储罐整体漏热量的23%，保冷层增加700 mm,漏热量比例减少5.8%，说明在此区间范围内增加保冷层厚度具有一定的效果。

4)继续增加保冷层厚度，当θ=1 600 mm时，罐底的漏热量占最大允许漏热量的3.18%，保冷层增加400 mm，漏热量仅减少1%，说明继续增加保冷层厚度对储罐保冷性的优化意义不大。

4 结束语

通过对LNG储罐罐体进行温度场的计算结果进行分析，发现保冷层两侧存在较大的温差，说明加入保冷层能有效地阻止储罐的漏热，增加储罐的保冷性。计算结果还显示出，罐底的漏热量占储罐整体漏热量的比例接近一半，说明针对罐底的优化更能有效减少储罐的漏热。所以在今后设计LNG储罐的时候，应该重点考虑罐底部分的结构设计。

根据储罐的设计参数计算，保冷层厚度为520 mm时，罐底的漏热量占最大允许漏热量的9.6%，当保冷层厚度增加至1 200 mm时，罐底的漏热量占最大允许漏热量的4.2%，罐底漏热占储罐整体漏热量的比例降至为23%；当继续增加保冷层厚度时，发现漏热量减少的效果并不明显。所以在今后设计LNG储罐的时候，从经济性的情况考虑，不能一味地增加其保冷层厚度，而应该找到保证保冷效果情况下最经济的方案。