一般无人船舶推进轴系的仿生抗振设计与冲击响应分析

杨明宇，董良雄

(浙江海洋大学 船舶与海运学院，浙江 舟山 316022)

船舶动力装置是船舶的心脏，而动力装置的核心部分是推进轴系。在实际航行过程中，船舶航行环境错综复杂，特别是某些无人船舶由于其特殊的工作环境和独特的船体结构，对推进轴系的安全性要求更为严格，所以为了保证船舶在特殊环境和作业下的安全，需要结构合理、强度足够、安全可靠的特殊轴系传动形式。国内外大量专家学者都对此进行了很多研究，并且设计出一种新船型——小水面线双体(SWATH)船来应对复杂多变的作业环境。国内很多学者也对推进轴系做了很多研究，比如王欢[1]利用低速柴油机的扭转振动模型来进行对船舶轴系时域振动的研究，但是并没有考虑到船舶受到冲击时，其推进轴系也会产生异常振动；杨佩东[2]利用SolidWorks建立了万向联轴器模型，对其进行了模态分析，然而只是单一研究万向联轴器，缺乏对整体推进轴系的分析; 高治华[3]建立了详细的万向联轴节数学理论模型，但是没有进行完善的仿真分析。因此，本文在模型简化的基础上，采用了双十字头万向联轴器，并且利用生物仿生思想设计了一套新型斜轴传动结构，针对该结构建立了无人船推进轴系模型，并且分析了冲击过程，总结了碰撞冲击力对无人船轴系的影响，有助于提升无人船的工程适应性。

1 船舶推进系统特点与设计要求

无人船多采用电力推进系统，该系统由原动机、发电机、输电配电系统、电动机、螺旋桨及控制设备组成。由于该无人船有独特的船体结构,电机主机不能布置在水下筒形潜体内,而是要安置于水上船体结构中,螺旋桨轴及推力轴安装在水下潜体内,使电机主机输出中心线与螺旋桨轴中心线之间形成高低差。图1为电机斜轴传动输出端示意图。图1中，L1为主动轴长度，mm；L2为从动轴长度，mm；实线代表联轴节初始位置，虚线代表联轴节受力变化后位置，起始角为r1；受力变化的角度为r2；H为从动轴到主动轴垂直距离，mm；d为万向联轴节直径，mm。

图1所示的轴系具有传动性能优越、工艺性好、经济性好的优点，但是由于存在高低差，振动很大，因此采用斜轴传动的结构，并且利用生物仿生的思想对万向联轴节的结构进行改造。

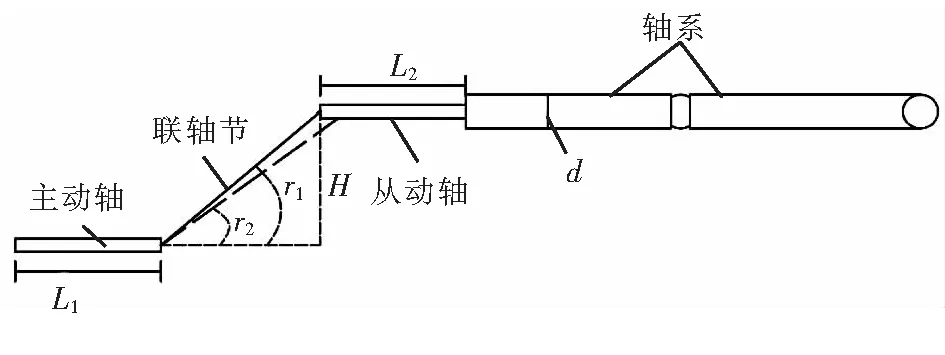
图1 电机斜轴传动输出端示意图

2 基于仿生机构的轴系联轴节设计

自然界中哺乳动物多采用腿式移动方式，其关节奇特而巧妙的结构形式,使得肢体可以灵活地相对躯体进行全方位连续的偏摆运动,这种摆动正是腿式移动的基础，而这种仿生结构给推进轴系联轴节的抗振设计提供了重要的启示。本文利用动物骨关节减振吸能的特性并且结合斜轴传动特点，重新设计推进轴系的传动结构，通过对双十字万向节进行改进，将双十字万向节的输入轴和输出轴改用球齿轮代替[4]。生物关节仿生结构示意图见图2，双十字万向节示意图见图3。

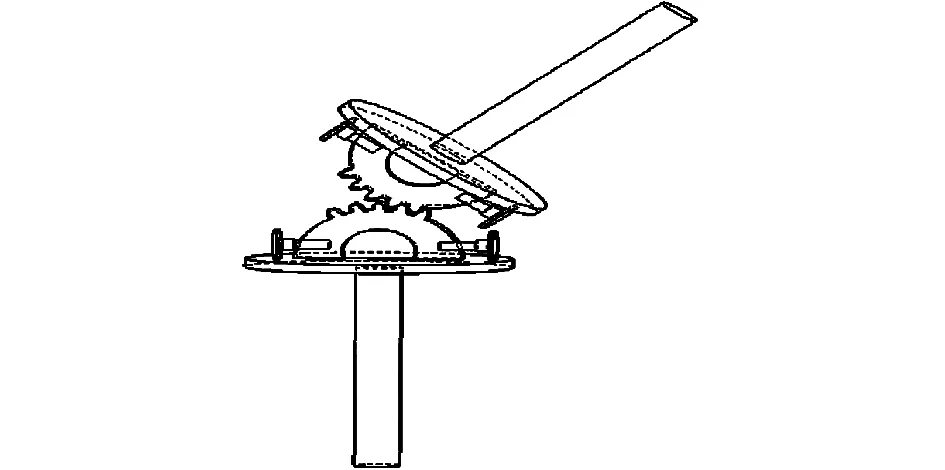
图2 生物关节仿生结构示意图

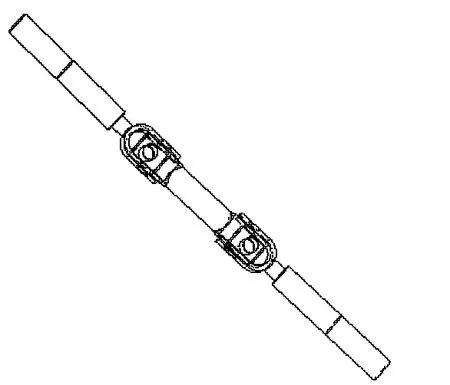
图3 双十字万向节示意图

图2中，球齿轮完全实现生物关节运动的条件主要是球心距保持不变,这是球齿轮能够正常啮合的条件，并且球齿轮可以进行空间两自由度的运动和动力传递，处于啮合状态的球齿轮在传递运动中可以等效为纯滚动的球面，而且球心距保持不变，始终等于两球齿轮节球半径之和；但是想要完全实现生物关节运动，不但需要球心距保持不变，更需要球齿轮能够以球心为基点进行全方位偏摆。所以可以将2种机构结合,用双十字万向节作为球齿轮的保持架,保证球齿轮传动的运动实现。而球齿轮不仅可以传递运动,同时还可以传递力,这个特点正好可以弥补双十字万向节使用中的不足。

3 推进轴系的动力学模型构建

首先，以某小型无人船为实例建立仿生轴系对象，其密度为7 850 kg/m3，电动机转速为350 r/min，激振力频率为5.83 Hz。表1为某无人船推进轴系各轴段属性。

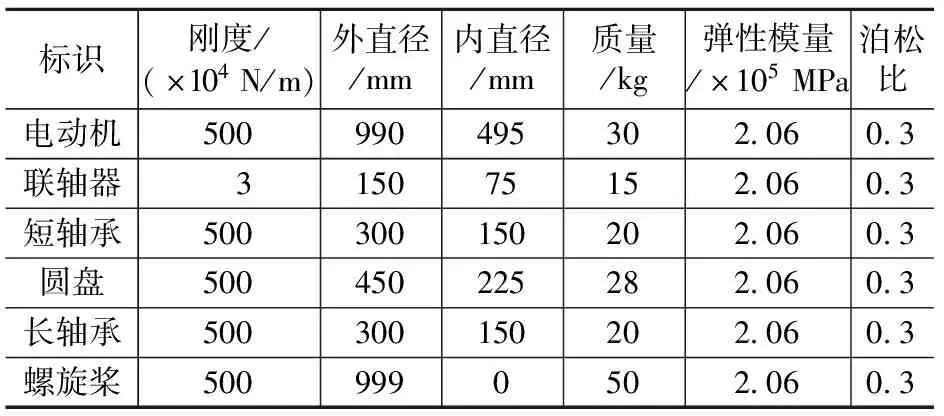
表1 某无人船推进轴系各轴段属性

模型建立好之后，进行网格的划分，将网格设置为0.2 m×0.2 m大小，共计248 831个节点和71 868个单元[5]。

4 仿生关节轴系的静力学模态分析

4.1 理论基础

通过对仿生推进轴系进行模态分析[6]，求解其固有频率和振型，从而分析是否存在共振现象。在一般运动系统中，动力学的通用运动方程为：

(1)

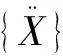
假定为自由振动并忽略阻尼，则为：

(2)

若结构以某一固有频率振动，即{X}=sin(ωt+φ)(t为时间，φ为相位角)，代入式(2)，可得：

以100 mL复原奶为准，在接种量0.1%，黄精浸提液0.5%，于42℃下发酵6 h，在每100 mL复原奶中分别添加蔗糖5%，6%，7%，8%，9%，按照1.3.1的工艺流程制造黄精酸奶，考查不同蔗糖添加量对黄精酸奶品质的影响，确定蔗糖的最佳添加量。

[K]-ω2[M]{φ}={0}。

(3)

由公式(3)可得，{φ}={0}是其中的一个解，其为结构中的所有节点都处于静止状态。因此为求非零解，要满足det[K]-ω2[M]=0，求解出的ω即为结构自由振动时的固有频率。由于通过上述微分方程，无法求得解，所以通过有限元法进行特征值求解。

4.2 强度分析

为了保证推进轴系正常运转，通过结合动力学模型和数学模型，先进行ANSYS静力学仿真分析。结果显示，推进轴系整体应力值不大，主要受力部位集中在万向联轴节处，应力大小为143.51 Pa，又因为采取的是45钢结构材料，最大应力小于屈服应力强度，所以满足设计要求。

为了确定轴系与轴承之间各阶固有频率和振型图，本文对船舶仿生推进轴系进行了模态分析，并且针对前20阶振型进行了求解。通过分析求解结果，可知随着振型阶次提高，模态固有频率逐渐增加，其中第1阶频率(即轴系最小固有频率)为7.277 Hz。并选取推进轴系第1阶、第10阶、第16阶和第20阶作推进轴系模态振型云图分别如图4～图7所示。振型反映了船舶结构在某阶模态下的相对位移变化，由图4～图7可知，推进轴系的振动表现形式多样，通过模态计算和分析结果可得[7]以下结论。

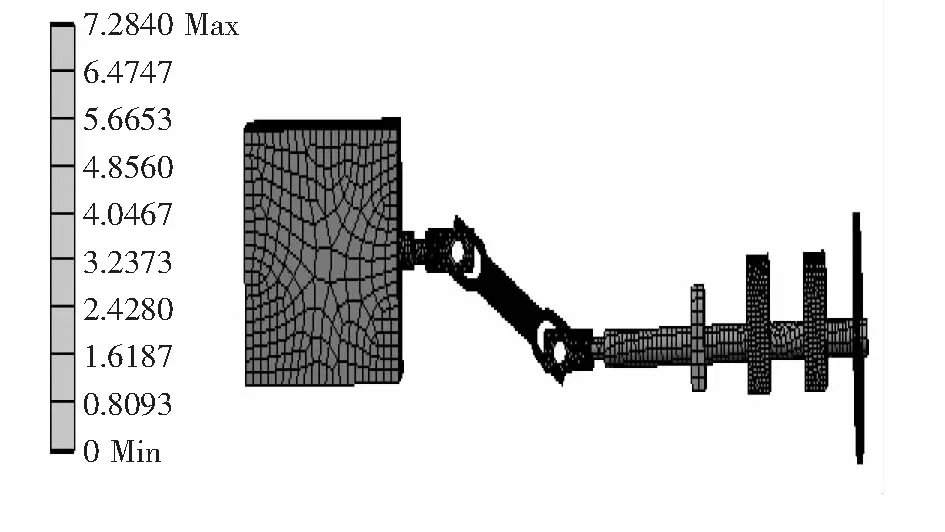
图4 推进轴系第1阶振型云图

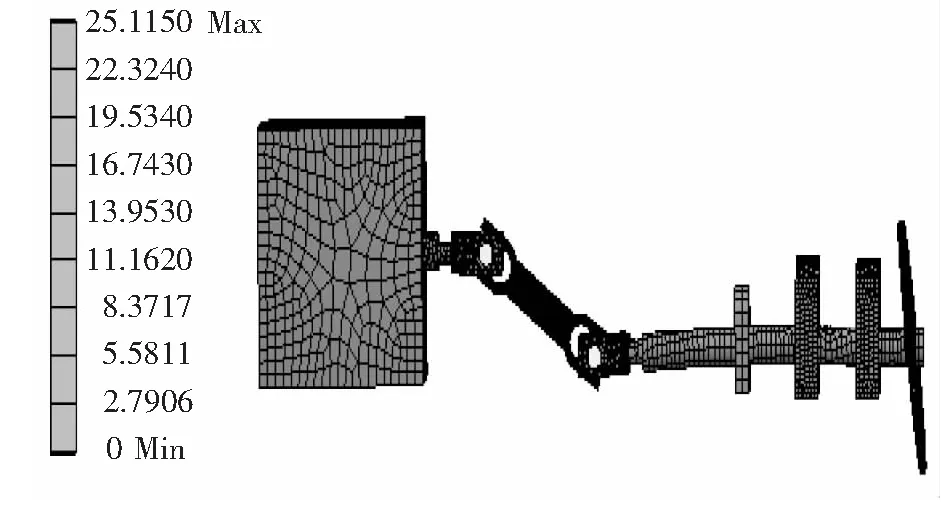
图5 推进轴系第10阶振型云图

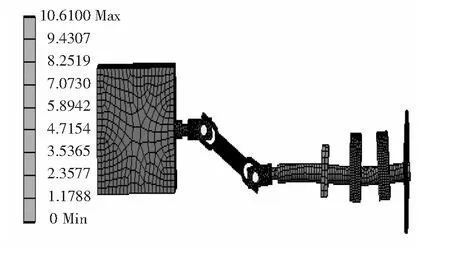
图6 推进轴系第16阶振型云图

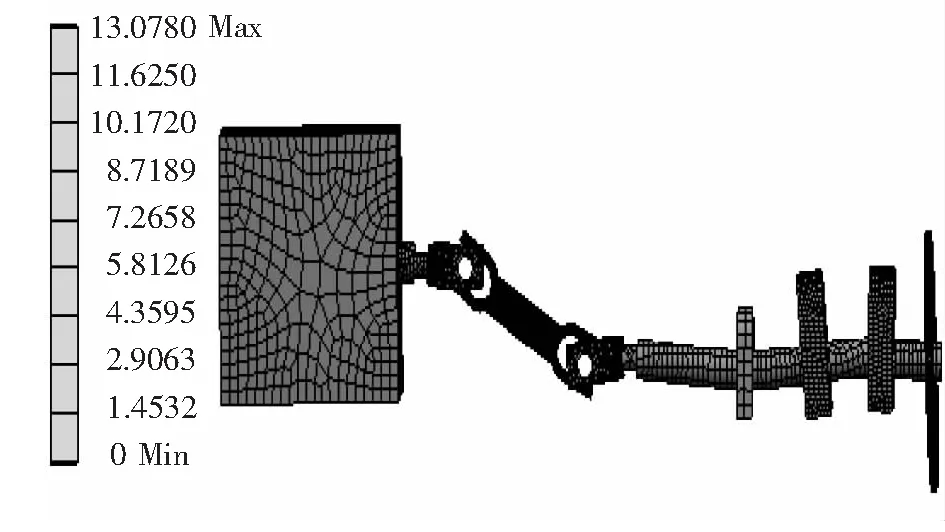
图7 推进轴系第20阶振型云图

1)由于轴系激振力频率ω0=5.830 Hz，小于轴系最小固有频率ω1=7.277 Hz，因此，改进后的仿生推进轴系仍能与原动力装置相匹配。

2)通过对推进轴系最大应力应变值云图进行分析得知，最大应变发生在万向联轴节处，最大等效应力值为143.51 MPa，小于45钢的最大屈服应力355.00 MPa，满足使用要求，结构安全。

3)第10阶振型图表现螺旋桨在推进轴系的扭转现象；第16阶振型图和第20阶振型图主要表现推进轴系中轴承的轴向振动位移，而且产生了一定程度的扭转摆动，这种扭转摆动会对船舶在航行过程中的安全造成一定程度的影响。在这些振型上可以看出，在5～1 000 Hz范围内，推进轴系容易出现不同程度的变形，且容易出现螺旋桨失稳现象，所以航行过程中要避免这种频率的激励，并且还需要对螺旋轴进行进一步的研究。

5 推进轴系谐响应和冲击响应分析

5.1 谐响应分析

谐响应分析用于确定结构在承受随时间按正弦变化的载荷时的稳态响应[8]，运动方程为：

(4)

其位移响应为：

{X}={A}sin(θt+φ)，

(5)

式中,{A}为位移幅值向量，θ为激振力频率。

将式(5)代入式(4)中可得：

{A}=[-Mθ2sin(θt+φ)+Ksin(θt+φ)+Bθcos(θt+φ)]-1·{F}sin(θt)。

(6)

式(6)无法求出解析值，所以利用有限法求解，设定θ的频率范围与频率间隔，计算其位移值，就可以得到位移、频率之间的关系，进而得出曲线的峰值频率。

综合仿生轴模态分析结果，可以看出在各阶固有频率的模态振型中，易产生最大变形位置的是螺旋桨轴处，所以针对此位置分别进行一般常规斜轴推进轴系和仿生斜轴推进轴系轴的谐响应分析比较。本文选取频率区间为5～1 000 Hz，总阶数选择为30阶，螺旋桨的X、Y、Z方向响应频率曲线分别如图8～图10所示。

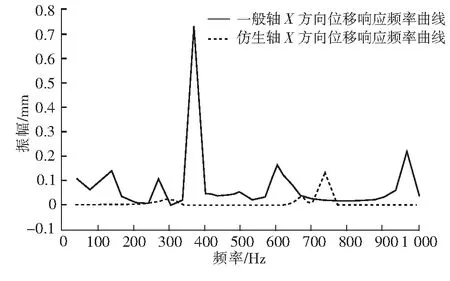
图8 X方向位移响应频率曲线

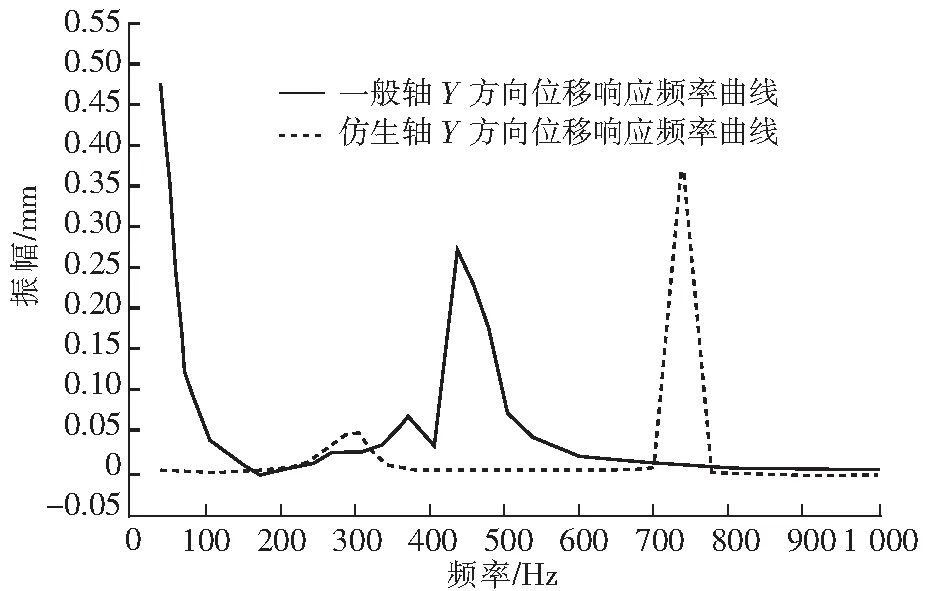
图9 Y方向位移响应频率曲线

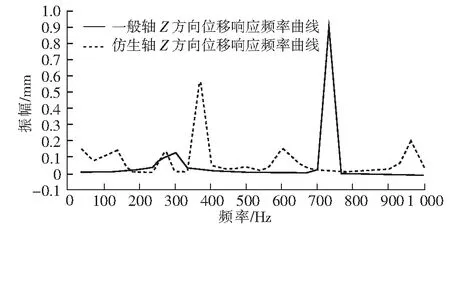
图10 Z方向位移响应频率曲线

由上述仿真结果可知，仿生轴推进轴系中的螺旋桨在X、Y方向的敏感频率为747 Hz左右，在Z方向的敏感频率落在380 Hz左右，且最大振幅发生在螺旋桨边缘的Y方向，大小为0.386 37 mm；一般轴推进装置中螺旋桨X方向的敏感频率落在375 Hz左右，Y方向的敏感频率在38 Hz左右，Z方向的敏感频率在748 Hz左右，且最大振幅发生在螺旋桨的Z方向，大小为0.895 01 mm。通过结果分析可以看出，在选定的频率范围内，仿生推进轴系在不同响应方向上的振幅变化情况较一般推进轴系更加稳定[9]。

5.2 冲击响应分析

针对船舶推进轴系的特点，采用ANSYS/Lsdyna软件进行船舶冲击响应的数值模拟，并且在不同船舶推进轴系工况下，受到同一外力的冲击，选择没有明显变化区域的同一个节点，得到其振幅图,一般轴和仿生轴在不同方向上的冲击振幅响应图分别如图11～图13所示[10]。

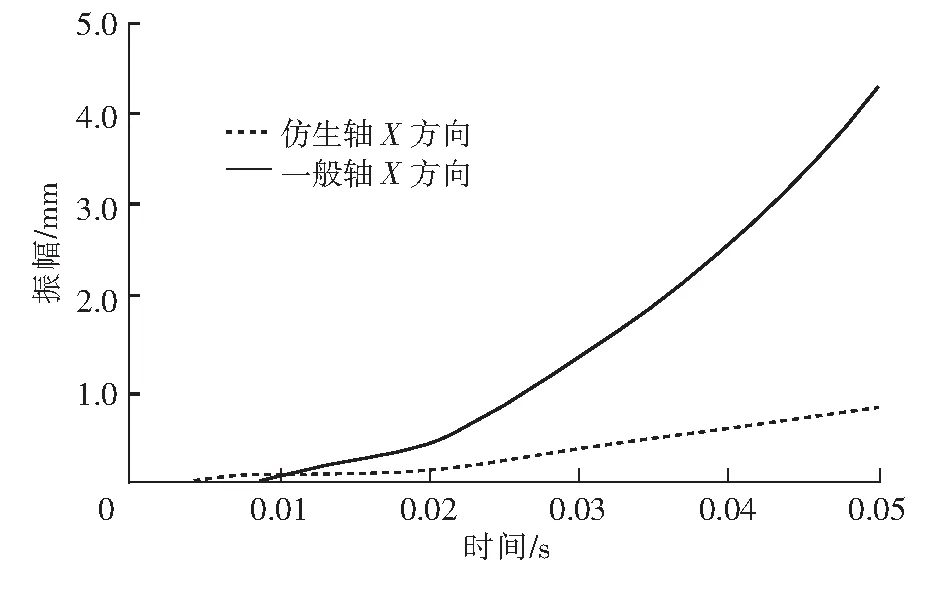
图11 一般轴和仿生轴X方向振幅

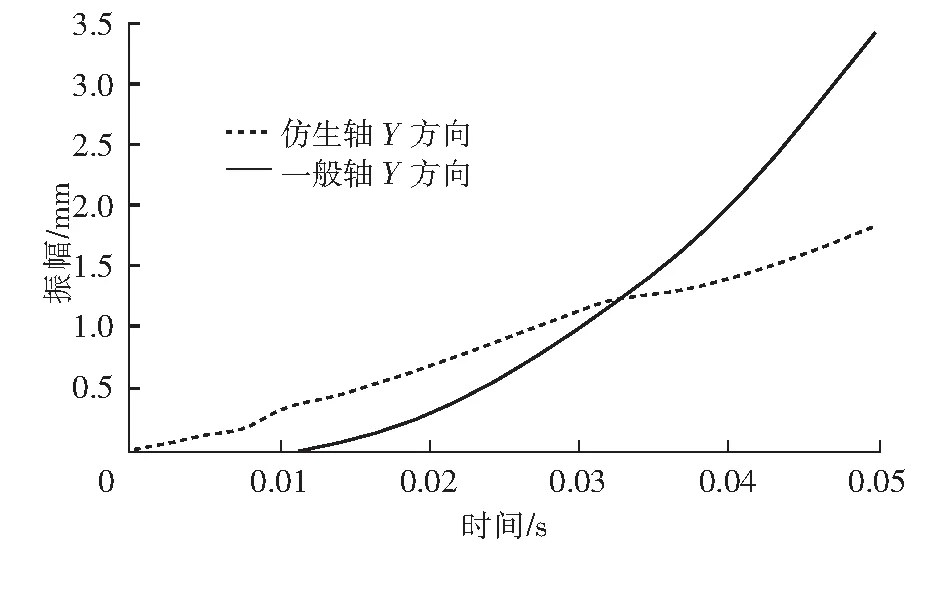
图12 一般轴和仿生轴Y方向振幅

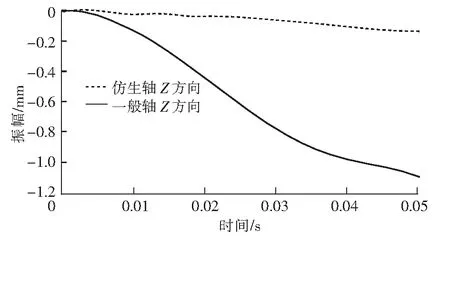
图13 一般轴和仿生轴Z方向振幅

从图11～图13可以看出，在设置相同的外界冲击载荷和航速时，仿生推进装置在X、Y、Z方向上的振幅与一般轴系振幅不一样，可以得到结论如下。

1)仿生轴推进装置受Y方向的冲击影响较为明显，在0.05 s时达到了振幅最大值1.8 mm；在X和Z方向受到冲击影响的振幅响应比较小，振幅分别为0.9 mm和0.1 mm，振幅上升趋势要比一般轴要小，抗振性能要优于一般轴。

2)本文研究的3个方向的振动幅值均不相等，但仿生轴的冲击响应振幅图变化趋势大致相同，且相对于一般轴来说，振幅波动随着时间的增长更趋于稳定，这表明了仿生轴在受到外界冲击时的稳定性要优于一般轴，振动幅度变化不明显。

6 结束语

本文探讨联轴节的抗振设计技术，通过生物仿生思想对联轴节进行优化设计。进而利用Solid-Works软件建立了仿生轴系的动力学模型，然后计算了频率与轴系转速对轴系冲击振幅程度的影响，最后进行谐响应和LS-dyna冲击响应分析计算，数值模拟得到的结论如下。

1)通过对推进轴系的静力学和模态分析可知，推进轴系的激振力频率小于第一阶模态的固有频率，不会发生共振破坏；之后研究了其前20阶固有频率和振幅云图，可知变形最为明显的区域在螺旋桨轴处，可针对此处的抗振设计进行进一步的研究。

2)通过进行谐响应分析，得知仿生轴敏感频率范围落在748 Hz和380 Hz附近，在工作时，应该避免这些频率段的激励。

3)通过LS-dyna的冲击响应分析，得到了振幅时域图，结果表明仿生轴系在受到外界一定的冲击时，振幅变化要比一般轴小，航行过程中更为安全稳定。