基于工况优选的燃烧优化典型样本库的建立

田伯尧，邓拓宇

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引 言

近年来，清洁能源发展迅猛，装机规模增长迅猛。但在可再生能源发展的同时，也存在着一些问题，由于清洁能源发电的间歇性、随机性较强，难以被我国电力系统消纳，在某些地区存在着严重的弃风和弃光的现象。为了解决可再生能源消纳的问题，《电力发展“十三五”规划》中提出，要全面推动燃煤机组灵活性改造，提高机组的调峰能力[1]。这就会使火力发电机组经常或长期处于低负荷的运行状态。机组处于低负荷状态下，会出现诸多问题，如燃烧不稳定、管壁超温和再热汽温偏差大等问题[2，3]。

针对机组在低负荷下燃烧存在的诸多问题，国内外诸多学者都做出了不懈的努力。对于低负荷下锅炉的燃烧稳定性，MARCEL Richter[4]针对提高一次风与磨出口温度以及降低一次风率提出了几个潜在的技术措施。HUSSAM Nosair[5]对燃煤电厂的灵活性要求的适应实施进行了归纳总结，分别从技术、运行维护、人员技能等方面进行了探讨。WANG Qingxiang[6]提出了一种新型的偏心二次风旋流燃烧器。赵星海[7]等通过选取多种富氧配风方式进行性能参数优化试验，提出了改进措施，提高了燃烧器的稳燃性能。王战锋[8]等进行了制粉系统优化和燃烧调整。在无设备改造的前提下，实现了锅炉在低负荷稳定燃烧。为了解决和改善机组在低负荷运行时出现的锅炉管壁超温和再热汽温偏差等问题，芮文明[9]等针对300 MW低负荷锅炉管壁超温现象，对其进行分析，并做出相应的实验调整以改善此现象。王小华[10]等对燃烧器区域拉杆进行调整，来改善管壁超温现象。周文台[11]等为了消除低负荷时的再热偏差，通过实验测试再热汽温偏差的原因，并给出在磨煤机出口安装煤粉分配器的解决方法。宋文雷[12]等通过对一、二次风调整来提高再热汽温。

对于低负荷下燃烧存在的问题，可通过相应的参数调整实验来解决和改善，但在实验中，需要调整的相关参数多、工况多，导致参数调整实验复杂、工作量大，无法在短期内得到使机组在全工况下安全稳定运行的最佳参数。因此提出了一种典型工况的优选策略，该方法利用电厂的历史运行数据，结合移动最小二乘法找到最适合做参数调整实验的典型工况。电厂对典型工况进行参数调整实验并利用三次样条插值方法建立典型样本库，未涉及的工况参数可通过对比典型样本库的数据进行调整。为电厂进行燃烧优化实验节省时间和精力。

1 研究思路及方案

1.1 燃烧优化方案

大量理论研究和实验证明，风与煤全燃烧过程、全锅炉运行工况、动态精确配比对于提高煤粉锅炉效率和降低NOx排放具有非常重要的作用[13]。但现有锅炉燃烧控制系统只能保证风煤总量配比的准确性，不能发挥多个独立调节手段共存的优势保证燃烧过程中不同燃烧阶段的风煤最佳配比、最优火焰中心和最优配风形状等影响锅炉效率和NOx排放量的关键参数。本课题组提出了一种前馈反馈复合优化控制煤粉锅炉燃烧的方案[13，14]。依据运行人员经验和燃烧调整实验数据来获得前馈信号，反馈信号的获取则是基于锅炉热力运行特性和规律。在不同工况下自动精确调节锅炉各个燃烧器的煤量配比、各台磨煤机一次风配比、各个磨煤机出口温度、各个燃烧器二次风量及燃尽风量配比，使锅炉燃烧效率和NOx排放量处于最佳状态。该方案的具体逻辑图如图1所示。

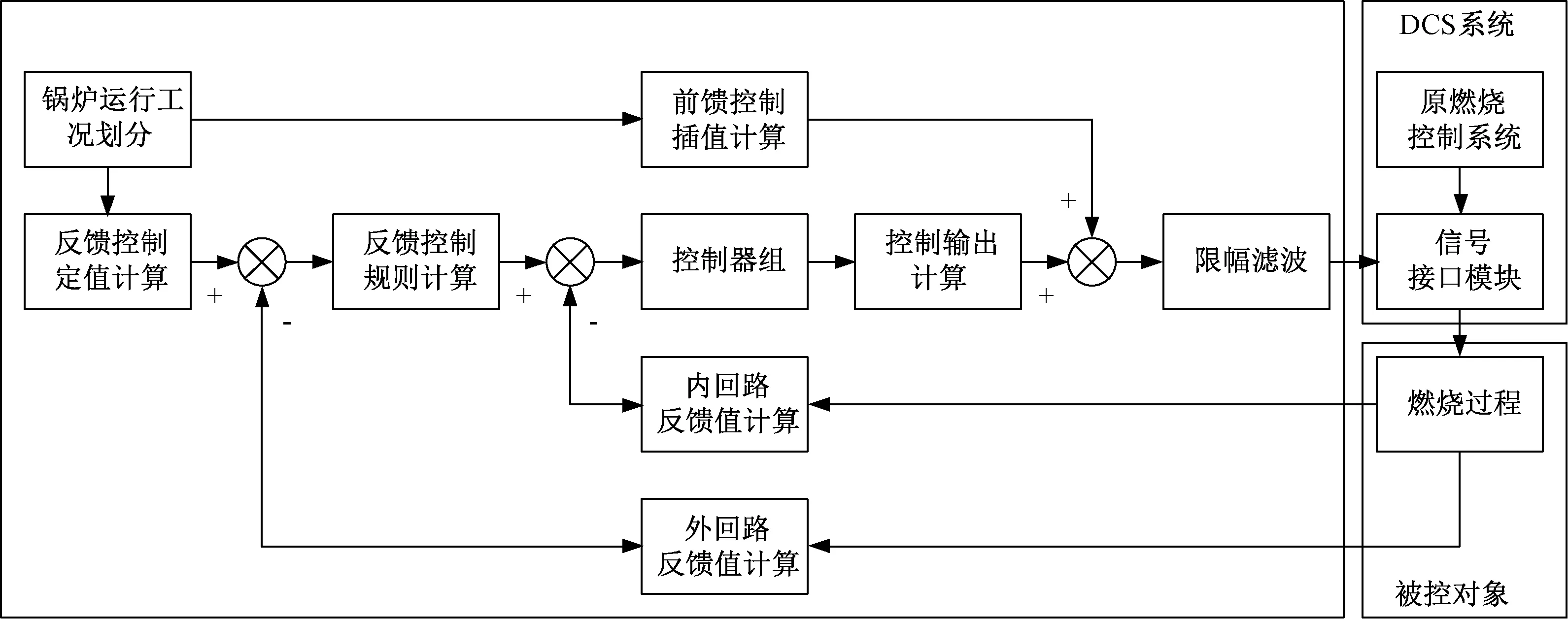
图1 燃烧前馈反馈复合优化控制系统[13]

1.2 典型样本库的建立

通过燃烧调整实验可获得每一个合法运行工况下使锅炉燃烧状态达到最优时燃烧优化控制信号的输出值，这些最优的输出值作为前馈信号保存在前馈控制插值计算模块中。前馈信号包括过量空气系数修正值、一次风压偏置值、二次风压偏置值等，然后将这些前馈信号数值保存在一个样本库中。这样在任一合法工况下的燃烧优化控制前馈信号输出值，都可在此前馈控制信号样本库中得到。

一般合法的磨煤机投运情况是指：锅炉处于运行状态的磨煤机所对应的燃烧器，尽量采用前后墙对冲的燃烧方式且不出现隔层燃烧或前后墙两层及以上燃烧器同侧单墙燃烧的情况；对于四角切圆燃烧方式则要求不允许出现两层及以上隔层燃烧的情况，锅炉实际运行过程中不允许出现非法的磨煤机投运情况[13，14]。

由于前馈控制信号多，再加上在现场做燃烧调整试验的限制，不可能在短时间内利用燃烧调整实验得到每一个合法工况下的最优前馈控制信号的输出值。因此提出了一种典型工况优选的方法，目的是简化燃烧调整实验，节约其消耗的时间和精力。该方法的主要步骤包括：

(1)锅炉工况划分;

(2)典型工况的选取;

(3)样本库的建立。

首先根据磨煤机台数确定所有的运行工况数，列出锅炉在不投油助燃的最低负荷到额定负荷范围内所有的磨煤机投运情况的排列组合，即2台数个。然后根据运行规程确定Y个合法的工况点。

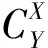
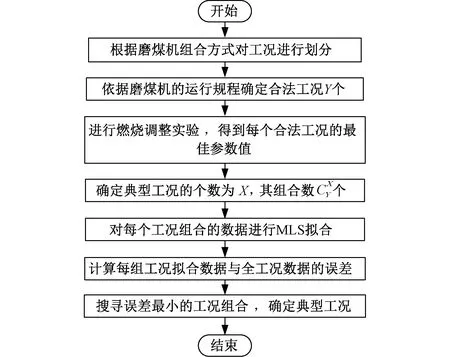
图2 典型工况优选流程图

最后电厂通过对典型工况进行调整实验，并利用三次样条插值方法建立典型样本库，未涉及的工况可通过对比典型样本库进行调整。

2 算法介绍

2.1 移动最小二乘法

移动最小二乘法[15-17]的具体原理如下，首先，在拟合区域的某个局部子域上，将拟合函数表示如下形式：

(1)

式中：α(X)=[a1(X),a2(X),…,am(X)]T为待定系数，它与坐标向量X有关，X=[x1,x2,…xn]；pi(X),(i=1,2…m)称为基函数，m是基函数的系数。对于一维问题,

线性基p=[1,x]T,m=2

(2a)

二次基p=[1,x,x2]T,m=3

(2b)

立方基p=[1,x,x2,x3]T,m=4

(2c)

为了使局部近似值达到一定的精度，需使样本点处近似功能函数值和真实功能函数值误差平方带权最小，因此残差的离散加权范式为

(3)

式中：n为影响区域内的节点数目；f(x)为拟合函数；yj为x=xj处的节点值；yj=y(xj)，w(x-xj)为节点xj的权函数。要求出待定系数α(x)，式(3)应该取极小值。式(3)对α求导得

(4)

α(x)=A-1(X)B(X)Y

(5)

其中

(6)

(7)

YT=[y1,y2,…,yn]

(8)

将式(5)带入式(1),即可得到MLS拟合函数

(9)

式中：Ok(X)称谓形函数，k表示基函数的数

Ok(X)=pT(X)A-1(X)B(X)

(10)

权函数对于MLS算法拟合有着非常重要的作用和意义。由于其具有紧支撑性，因此其可以在拟合大量散点数据时进行局部处理。但是在拟合时如何选取合适的权函数，必须遵循几个原则：

(1)权函数的紧支撑性决定在每个节点处的权值在支撑域内时大于零，在支撑域外或者边界处等于零[17];

(2)必须具有单位分解性;

(3)权函数必须光滑连续可导；

(4)在支撑域内，即权值与距离成反比。

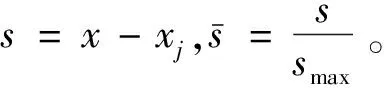
(11)

2.2 三次样条插值算法

为了准确的经过典型工况的数据，本文选择常用的三次样条插值函数(Spline插值函数)来确定余下工况的数据。三次样条函数的数学原理以及子程序，鉴于数学著作和文献，这里做做简单介绍。

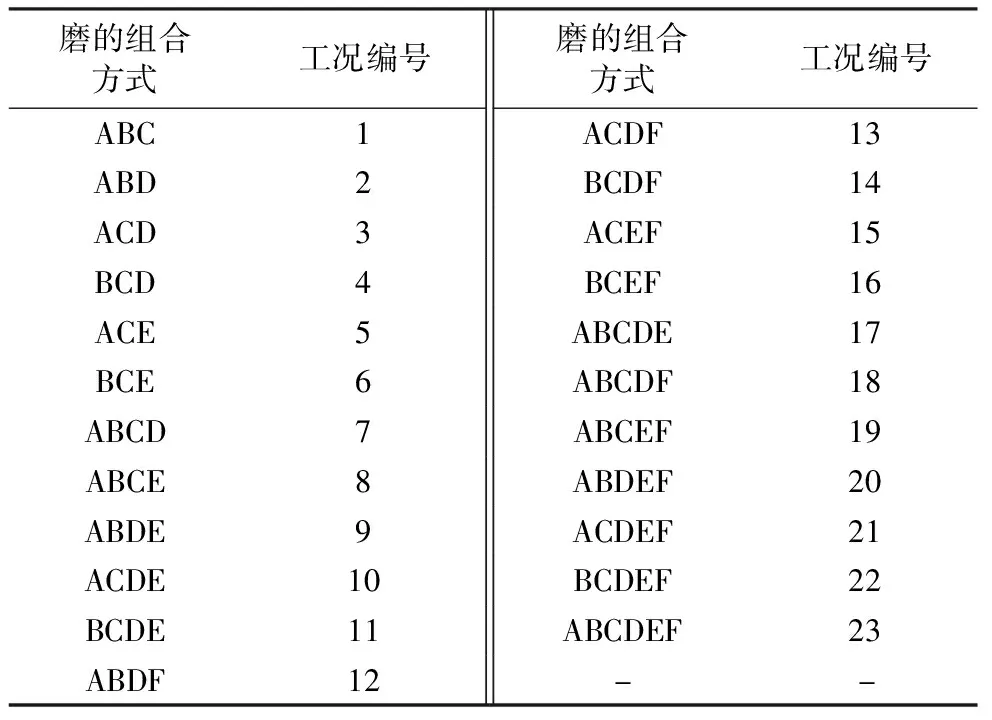
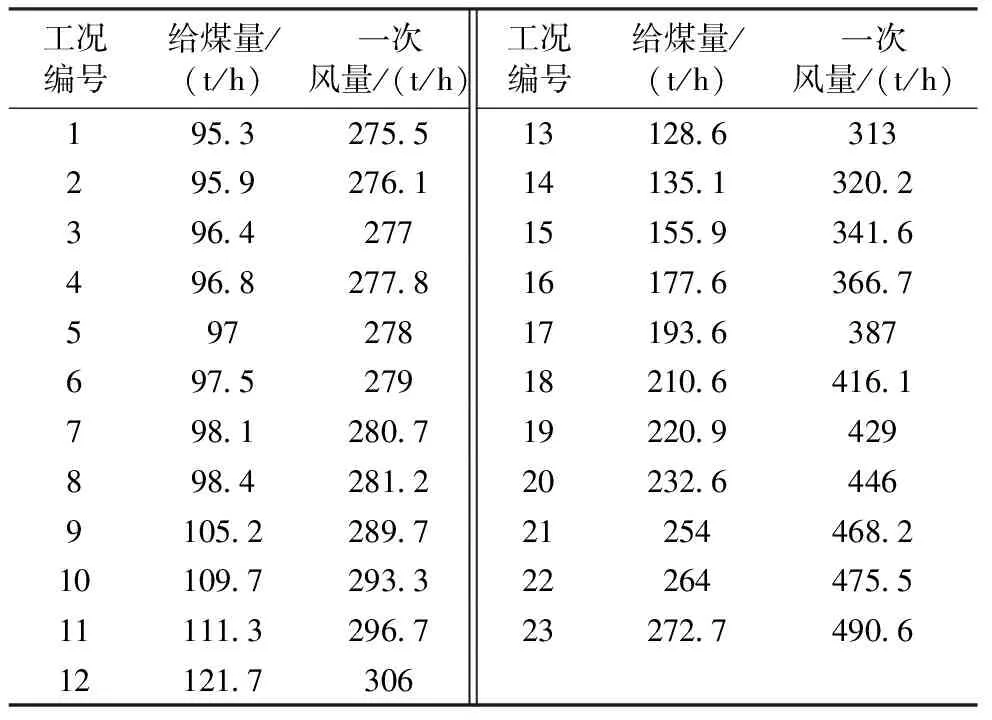
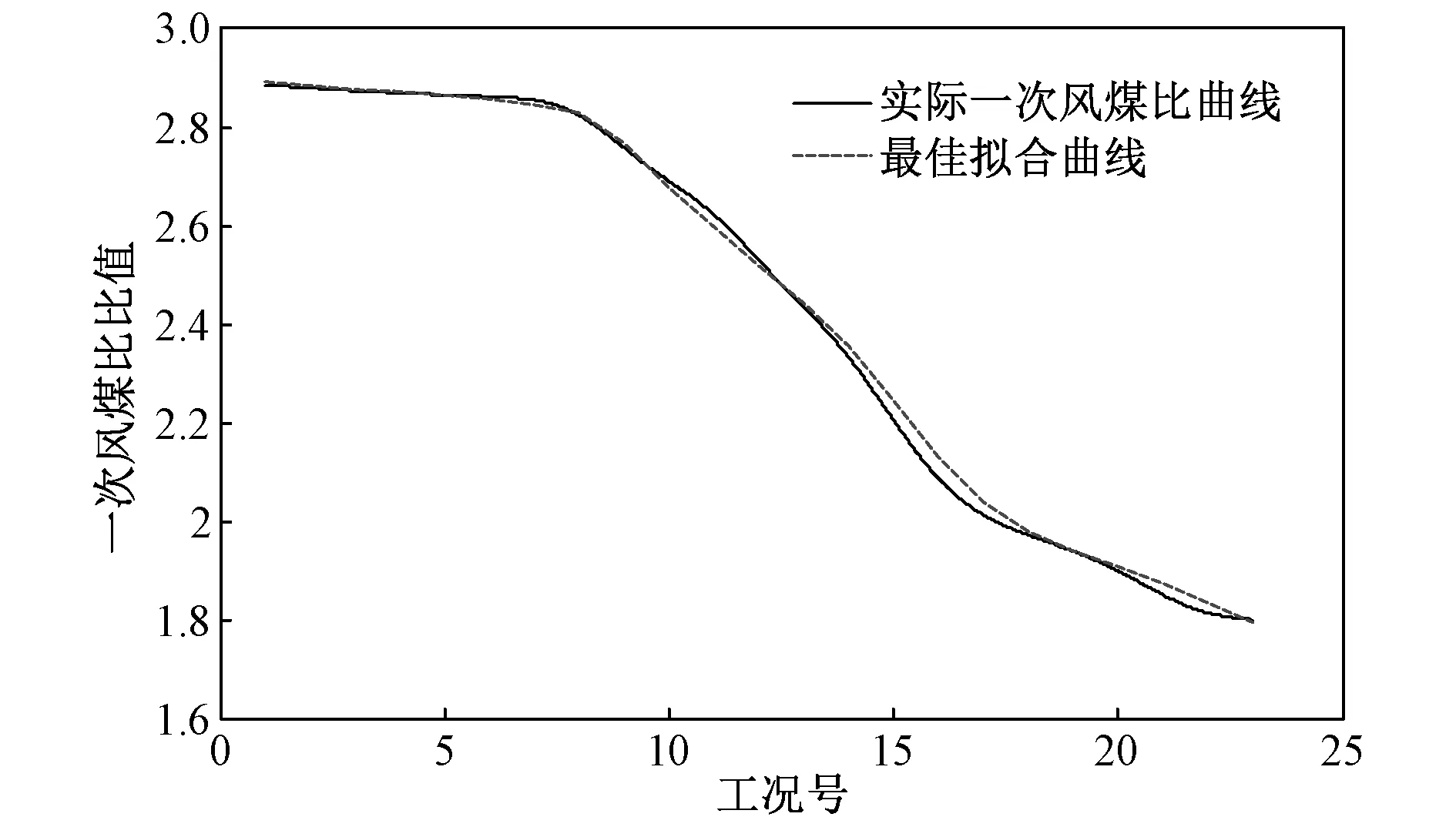
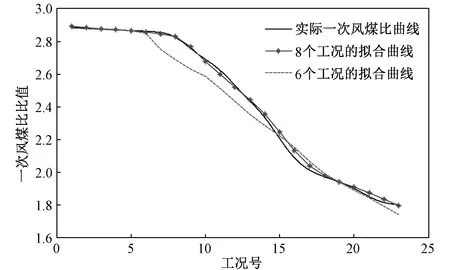
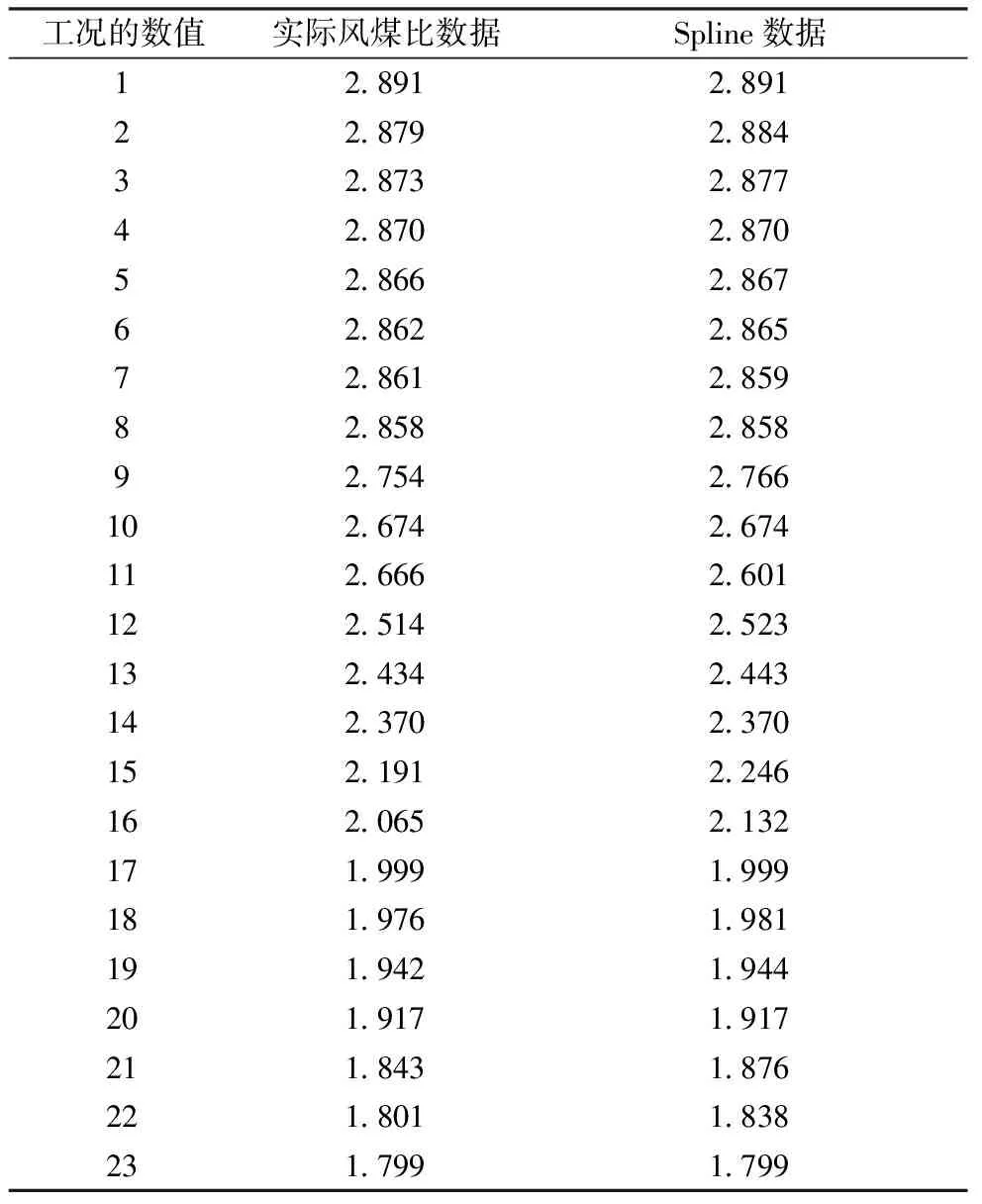
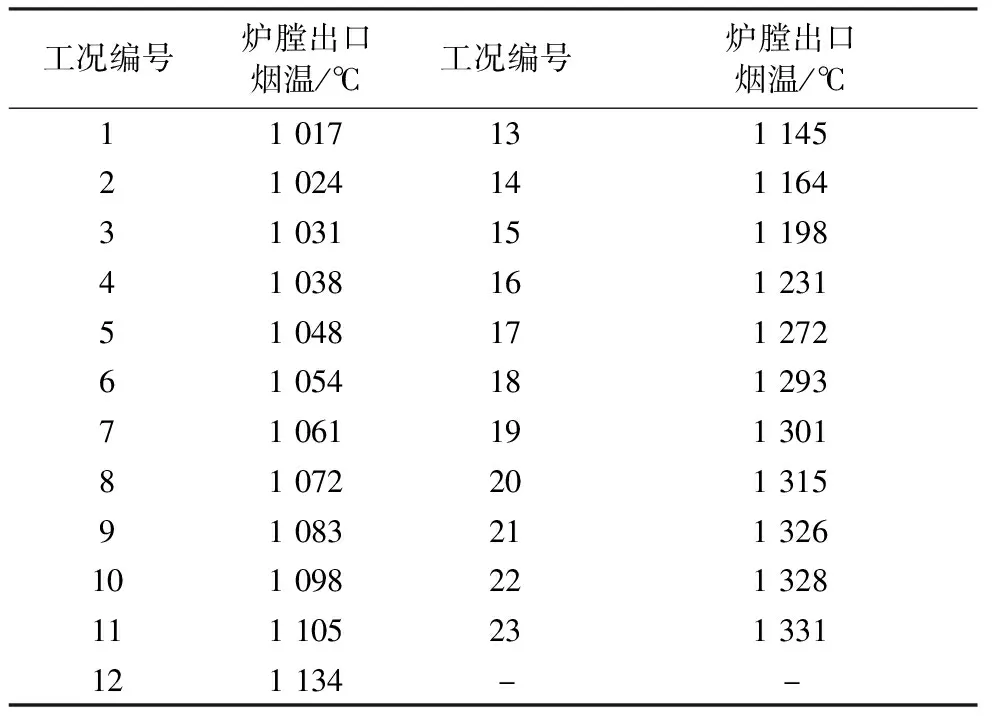
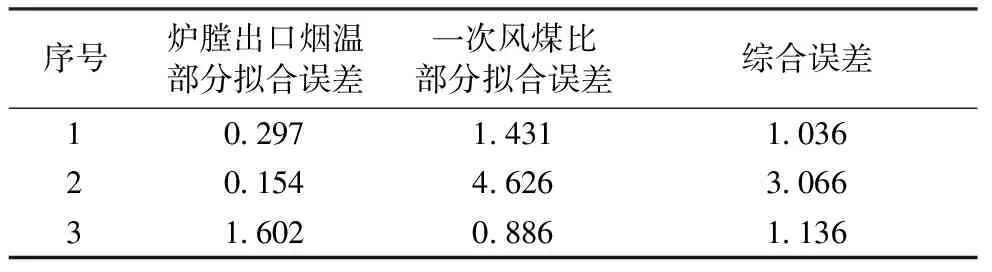
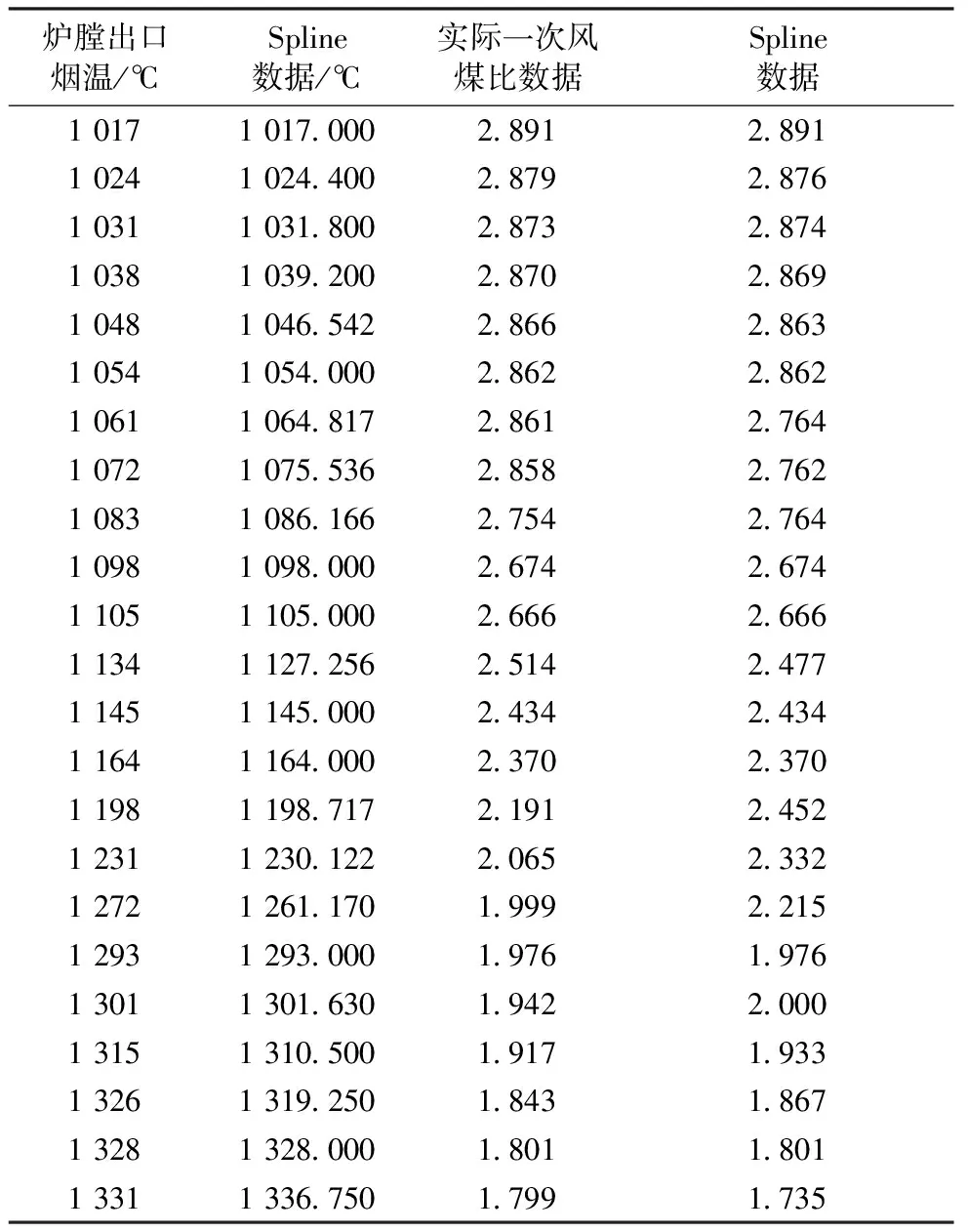
通常，在[a,b]上的以xi(i=0,1,2,…,n)为节点的三次样条函数[18-20]定义如下：给定区间[a,b]的一个划分Δ:a=x0

(1)一致通过n+1个插值点(xi,yi)，即S(xi)=f(xi)=yi(i=0,1,2，…n);

(2)二阶连续，即S(x)=∈C2[a,b];

(3)三次分段，即在每一个小区间[xi-1,xi](i=1,2，…n)上均为三次多项式。

则称S(x)为函数f(x)的三次样条函数。在构造三次样条插值函数时，为了确定S(x)应根据n+1个插值条件，3n-3个连续条件以及给定的边界条件，再利用节点处的一阶或二阶导数就可构造出三次样条插值函数。

3 电厂实例验证

3.1 方法验证

通过燃烧调整实验获取的前馈信号有很多，如过量空气系数、一、二次风压、各台磨煤机给煤量、各台磨煤机出口温度、各台磨煤机一次风量等，选取一次风煤比来验证该方法的可行性和有效性[13]。

所研究的对象为660 MW超临界锅炉，该炉采用单炉膛、一次中间再热、固态排渣，四角切圆燃烧方式。采用中速磨煤机正压直吹式冷一次风机系统，锅炉配6台中速磨煤机，布置在炉膛层侧面，每台磨煤机带同一层4只燃烧器。自下而上分别为A、B、C、D、E、F层。对于每台磨煤机来说，必定为启动或停止两种状态之一，因此6台磨煤机有64种启停组合方式。但是在电厂锅炉正常运行情况下，并非每种磨组合方式都被允许。将这64种磨煤机情况按照不允许出现两层及以上隔层燃烧的要求去除非法组合之后，剩余23种合法组合。为了方便数据处理，将这些工况进行编号，如表1所示。

表1 磨煤机的合法启停组合

为了能够得到使机组稳定运行的最佳参数，首先需要在每一个合法工况下进行一次风煤比实验，各合法工况下的一次风量和磨煤机的给煤量实验结果如表2所示。

表2 各工况的给煤量和一次风量

然后根据实际情况确定典型工况的个数，这里选取8个。为了准确地确定这8个典型工况，从23种合法工况中随机选取8个工况，可得到490314种工况组合方式，利用每种工况组合的8个数据并结合移动最小二乘法对剩余工况下的一次风煤比参数进行数值拟合，计算每组拟合数据与原数据之间的误差平方和。利用程序逐一比较每组的误差，误差平方和最小的一组组合即为典型工况。结果如图3所示。对比所有工况下的误差可得，ABC、BCE、ABCD、BCDE、ACDF、BCDF、ABCDE、ABCDEF工况组合的误差最小，为0.115。此工况组合包含3、4、5台磨煤机的运行情况，因此该工况组合的8个工况即为典型工况。

图3 实际与拟合一次风煤比曲线

3.2 工况个数对典型工况选取准确度的影响

为了发现选取典型工况的个数对整体方案的精确度的影响，随机选取6个工况进行比较。从23个工况随机选取6个工况，得到100 947种组合方式，通过移动最小二乘法对所有工况的一次风煤比参数进行数值模拟，并计算每组拟合数据与原数据之间的误差平方和，误差对比曲线如图4所示。根据对比所有工况下的误差，得到BCE、BDE、BCDE、ABDF、ABCEF、ACDEF工况组合的误差最小，为0.327。

图4 不同典型工况个数的误差对比

通过图4可以看出，选取8个工况拟合的曲线与实际曲线更为接近，而且误差较小。对6个工况进行一次风煤比调整实验比8个工况要节省一些时间，但是数据的准确度有所下降。若目的是尽快完成调整实验，为后续其它工作换取时间，可选取6个或7个典型工况进行调整实验；若目的是为了提高数据的准确性，就选取8个或8个以上的工况进行调整实验。电厂可根据自己的需要自行选择。为了验证该方法的可行性和数据的准确性，本次选取8个典型工况进行一次风煤比调整实验，将实验结果保存在样本库中，并利用Spline法对样本库进行插值，插值如表3所示，插值误差仅为1.76%。

表3 实际与插值一次风煤比数值

3.3 多个信号参数对典型工况选取的影响

参数调整实验往往是对多个参数进行调整，以确保机组的稳定性、安全性和环保性。多个参数确定典型工况，应综合考虑每一个参数对典型工况选取的影响，通过其中一个参数确定典型工况是不准确的，应考虑综合误差。下面以一次风煤比和炉膛出口烟温为例来进行说明。各工况下的炉膛出口烟温如表4所示。

表4 各工况下的炉膛出口烟气温度

针对两个信号参数对典型工况选取的情况，不仅仅要关注每个信号的拟合误差，还要着重考虑它们的综合误差。综合误差公式为

(12)

式中：σ表示综合误差；Zi表示每个参数对锅炉效率的影响因子，利用实验数据分别求出一次风煤比、炉膛出口烟温与锅炉效率的回归系数，根据回归系数的确定影响因子；Wi是拟合误差。因为不同参数指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理。首先将每一个工况下的数据按照式(13)进行min-max标准化处理，然后在利用文中的方法求得每一个参数的误差；根据实验数据得到一次风煤比、炉膛出口烟温与锅炉效率的回归系数分别-0.695与0.373，根据二者的回归系数算的影响因子分别是0.651与0.349。最后利用公式(12)得到综合误差，部分结果如表5所示。

表5 炉膛出口烟温与一次风煤比综合误差

(13)

从表5中可以看出，序号2中的炉膛出口烟温拟合误差最小，但一次风煤比误差拟合误差为4.626，远大于0.886，综合误差为3.066。说明在此工况下，炉膛出口烟温拟合准确度达到最佳值，但一次风煤比拟合误差值偏大。序号3中的一次风煤比拟合误差最小，但综合误差偏大。序号1虽然两个前馈信号的拟合误差并非最小，但其综合误差最小，因此序号1为代表的工况ABC、BCD、ABCE、ACDE、ABCD、ABCDE、ABDEF、ABCDEF为两个前馈信号下的典型工况，并从表6可以看出插值度也很高。

表6 炉膛出烟温与一次风煤比实际与插值数据对比

通过与3.1的结果进行对比可知，如果仅考虑一个参数的误差，得到的典型工况不能使机组运行达到最佳状态。

4 结 论

针对燃烧优化参数调整实验复杂、工作量大的特点，提出了一种基于典型样本库的烧优化方法。该方法利用电厂的数据，结合移动最小二乘法搜寻适合做参数调整实验的典型工况，对典型工况进行参数调整实验并利用三次样条插值建立典型样本库。

(1)单个参数情况下，如一次风煤比，拟合误差最小的工况组合即为典型工况。通过对这些典型工况做燃烧调整实验并利用插值得到的一次风煤比样本库数据与原数据误差为1.76%。

(2)改变选取工况个数会影响典型工况选取的准确度。如选取6个和选取8个工况相比，前者虽然会减少燃烧调整实验消耗的时间，但是会降低典型工况选取的准确度。

(3)多个信号参数选取典型工况需以综合误差为准，综合误差最小的工况组合可视为典型工况组合。