考虑可靠性与源荷双侧不确定性的多目标需求响应模型

赵冬梅，陶 然，马泰屹，王迎辉，王浩翔

(华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

随着电力市场化改革的不断深入，需求响应已经参与到电力系统运行的多个环节。目前，华东分调、新疆区调等区域在技术上已支持对需求侧的调控，并建设了多个示范工程。需求响应成为提升“源-网-荷”互动电网活性、削峰填谷、消纳新能源的有效手段之一[1]。

需求响应在提高系统可靠性、降低运行风险等方面的潜力同样值得关注。电力系统可靠性涵盖电力生产运行中发、输、变、配等过程中安全性和充裕性多个维度的考量[2]。在经济调度中主要关注供用电可靠性和传输可靠性。提高备用容量是提高系统供用电可靠性的主要手段，而备用目标与运行目标通常是有一定冲突的[3]。文献[4]以鲁棒调度为基础研究了综合能源系统的备用容量配置问题。文献[5]以电量不足期望(expected energy not supplied，EENS)和弃风期望为目标研究了旋转备用容量配置的问题。文献[6]则以EENS为约束实现备用容量的优化配置。文献[7]通过机会约束规划和蒙特卡洛模拟研究了系统阻塞情况下的调度问题。文献[8]基于条件风险价值(conditional value-at risk，CVaR)提出了两阶段随机规划模型。上述研究大多集中在优化之前选取某一固定比例的备用率或通过其他附加约束来确定这一比例，未能考虑源荷双侧的多重不确定因素，且固定备用比例的方法可能在某些时段同时丧失经济性和可靠性。

针对传输可靠性，文献[9]采用混合智能算法进行了连续潮流计算，并参考北美电力可靠性委员会(north American electric reliability council，NERC)的定义评估了线路传输可靠性。文献[10]采用序贯蒙特卡洛仿真模拟，研究了风储系统对传输可靠性的影响。文献[11]考虑风电不确定性提出了一种传输可靠性的快速评估方法。现有的研究是在优化中给出线路输电极限的约束条件，或在优化结束后进行可靠性评估，但鲜有从优化传输可靠性的角度对潮流分布进行调整，且高负载线路故障后可能会造成较为严重的影响。

同时，源荷双侧不确定性是影响经济性和可靠性的因素之一。提高新能源和负荷预测精度是适应不确定性并降低调度风险和成本的工程实用方法[12，13]，但在预测技术得到提升前，很难进一步提升电网活性。而需求侧资源在调度过程中具有不确定的响应行为[14]，这些不确定行为主要来源于激励程度、随机事件等。因此，以确定方式考虑的需求响应模型难以满足调度需求[15]。国内外学者在计及需求响应不确定性来降低系统运行成本等方面做了大量研究。文献[16]基于动态场景法以系统成本为目标对需求响应进行了研究。文献[17]通过分时电价机制和消费者心理学原理研究了可调负荷自发用电行为的改变。文献[18]将可调负荷的实际响应视为随机变量，采用随机优化来研究可调负荷响应的不确定性。文献[19]研究了考虑用户参与不确定性中的需求响应策略多时间尺度优化问题。文献[20]采用随机优化提出了需求响应参与的跨区互联电网分层调度模型。上述文献大多以系统成本、节能减排等经济性指标为主，并考虑了柔性负荷参与需求响应的不确定特性，而关注不可调度负荷的需求随机性、机组和输电线路的停运随机性等其他不确定因素以及可靠性指标的研究不多。

本文在现有研究的基础上，对系统中的多重不确定因素进行建模，研究需求响应对提升经济性和可靠性的作用，提出机会风险备用容量的配置方法，用机会约束规划构建多目标模糊随机优化模型。

章节设置和主要工作如下：

(1)源荷双侧不确定分析：研究机组故障停运、风电出力随机波动、刚性负荷需求随机波动、柔性负荷响应不确定等多重不确定特性。

(2)电力系统可靠性：分别研究供用电可靠性和传输可靠性，考虑源荷双侧不确定性。以电力不足概率为供用电可靠性指标，动态配置系统备用容量；以线路负载风险为传输可靠性指标，构造优化目标。

(3)模型与等价转换：构建多目标混合整数模糊随机机会约束规划模型，并根据不确定规划理论对含模糊变量和随机变量的约束条件进行等价转换。

(4)算例分析：从是否设置需求响应和不同备用配置方式的角度设计三种场景分析柔性负荷调度对各目标值以及可靠性的影响。并采用基于分解的多目标进化算法(MOEA/D)和熵权法求解此模型。

(5)结论。

1 源荷双侧不确定分析

源荷双侧的资源可以分为4类：1)常规机组；2)柔性负荷：以可削减负荷和可转移负荷为例；3)新能源发电：以风电为例；4)刚性负荷：系统中无供需弹性和无可调度能力的负荷。本节重点讨论柔性负荷、风电和刚性负荷的不确定性。常规机组的不确定性将在2.1节中讨论。

1.1 柔性负荷响应不确定性

根据用户调整用电行为是受价格影响产生的自发行为，还是签署合同或受政策约束产生的合约行为，可分为价格型响应和激励型响应。在价格型与激励型的分类下又可根据用户用电量的调整是否需要全部返还、部分返还或不返还分为可平移负荷、可转移负荷或可削减负荷。

(1)价格型与激励型需求响应

理性的用户根据电价自发的改变自身用电行为是具有一定规律和限度的。根据消费者心理学模型[21]将用户响应电价的程度分为死区、线性区和饱和区。在不同的区间，柔性负荷响应的不确定程度是不同的。在死区和线性区，电价对用户的激励程度有限，不确定性主要来源于非经济因素。柔性负荷响应率随着电价的上升而上升，而不确定程度也随之上升。在饱和区，电价对用户的激励程度足够大，经济因素占主导。受到柔性负荷自身响应容量的约束，转移率达到最大值并保持不变，不确定性也逐渐缩小至0。由于我国的实时电价机制还未完善，对于可转移负荷主要考虑基于分时电价的负荷响应率的不确定性。如图1所示。

图1 价格型需求响应“峰-谷”时段负荷转移率

(1)

式中：λp,v=(λp,v,1,λp,v,2,λp,v,3)为模糊变量，用三角隶属度描述，其隶属度函数如式(2)所示。

(2)

式中：λp,v,1、λp,v,2和λp,v,3分别为三角模糊变量的三个参数。

“峰-谷”负荷转移率的波动量如式(3)所示。

(3)

(4)

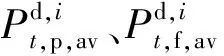
对于激励型响应，通常认为其用电行为由合同或政策保证，只要合同或政策的合理性与公平性得到保证，用户在主观上违约的可能性不大，即主观上无不确定性。但由于非主观因素，如预测误差等，客观上也会产生一定的不确定性，此时激励型响应在完成可削减或可转移的响应后，退化为刚性负荷，此部分的不确定性在1.3节中考虑。

(2)可削减负荷

可削减负荷除了在价格型和激励型上有所区分外，还需要由约束条件确定其响应特性[22]。主要包括可削减容量上下限约束、最大削减次数约束、最大削减速率约束、最大连续削减时间和最小削减时间间隔等。

可削减容量上下限约束：

(5)

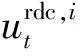
最大削减次数：

(6)

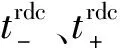
最大削减速率：

(7)

式中：vrdc,i为可削减负荷i的最大削减速率。

最大连续削减时间：

(8)

最小连续削减时间间隔：

(9)

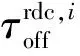
尽管，系统中已经存在不少削减量为连续值的可调度负荷，如充电桩集群、暖通空调集群等。但调节量离散的负荷仍大量存在此处。以分档调节的方式建模。

按档调节的可削减容量约束：

(10)

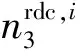
同时，按档调节的可削减负荷用户一个时段只能选择其中一档进行调节，需要满足约束：

(11)

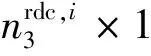
(3)可转移负荷

与可削减负荷类似，可转移负荷的响应同样需要满足一些约束条件。价格型可转移负荷由于依靠的是用户自发行为，在调度角度仅考虑激励型可转移负荷的约束条件。

可转移容量上下限：

i=1,2,…,Ntrans

(12)

式中：

(13)

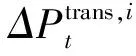
最大可转移次数：

(14)

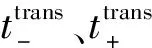
上述约束可以满足可转移负荷用户将负荷向未来时间段转移，或从未来时段转移到当前时段。若可转移负荷自身有生产时序的要求，即需要在连续时间段内的转移，可增加与式(9)类似的约束。对于可平移负荷，要求在转移过程中的用电量不变，可增加如下约束

(15)

1.2 风电不确定性

风电的不确定性一般来源于风速的不确定性，而影响风速的原因则十分复杂。对于调度而言，风电的不确定性表现为实际风电出力与预测风电出力之间的误差。本文采用平均值统计特性[23]来描述误差随机变量。如下所示：

(16)

(17)

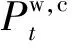
1.3 刚性负荷不确定性

不失一般性，将系统中原本就不具备可调度能力的负荷与面向售电商或负荷聚合商在完成柔性负荷调控后余下的负荷统称为刚性负荷。从调度的角度考虑，刚性负荷的不确定性表现为实际负荷与预测负荷直接预测误差的随机性。满足如下关系：

(18)

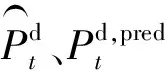
(19)

式中：k一般取1。

2 电力系统可靠性

2.1 供用电可靠性

供用电可靠性指不间断向需求侧供应电力电能的能力度量。其手段主要是通过提高备用容量来应对源荷双侧随机波动产生的系统充裕性事件[25]。当前配置系统备用容量主要通过事故备用和负荷备用两方面来确定，即将备用容量配置为：系统中一台最大机组的装机容量附加一定比例的负荷预测量。最大机组的装机容量通常是固定的，负荷预测的比例也根据系统长期运行经验来获得。上述方法缺乏备用容量配置与可靠性之间的联系，可能造成一定程度的资源浪费。本节以电力不足概率(loss of load probability，LOLP)为供用电可靠性指标。通过考虑源荷双侧不确定性的累积停运容量概率(capacity outage probability，COP)确定系统风险备用容量。

常规机组会因突发事件而停运，造成系统中的发电功率缺额。用式(20)描述。

(20)

(21)

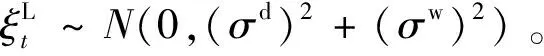
LOLP指系统在某一时刻的机组累积停运量与净负荷随机波动之和大于系统此时配置的备用的概率[26]。如下所示。

(22)

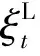
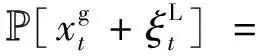
(23)

(24)

并设通过给定概率求机组累积停运容量的表达式为

(25)

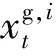
(26)

式中：

(27)

(28)

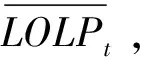
2.2 传输可靠性

传输可靠性指电力传输过程中，输电线路不间断传输的能力度量[29]。考虑线路传输约束的安全约束经济调度模型没有考虑线路故障产生的传输风险，难以实现对潮流分布的优化。同时，由于我国实时节点电价机制尚未成熟，也无法从供需关系上均衡线路负载来提高传输可靠性。

实际系统可以根据不同的线路负载率和负载时间长短对线路风险程度分为四类[30]：(1)长期负载水平(long time emergency rating，LTE)：根据不同季节，允许较长时间的线路负载水平，一般夏季4 h，冬季12 h；(2)短期负载水平(short time emergency rating，STE)：短期内不发生热稳定问题的线路负载水平，一般为15 min；(3)极限负载水平(drastic action limit，DAL):线路可以承受的极限负载率，一旦越限容易引起事故。采用分段线性函数来描述线路负载严重度和负载率之间的关系，如图2所示。

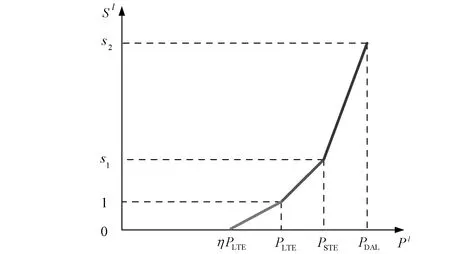
图2 线路负载严重程度与负载率的关系

(29)

(30)

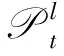
3 模型与等价转换

3.1 目标函数

本文考虑三个目标函数来实现受系统可靠性和不确定性影响的经济性、供用电风险和传输风险的优化。包含运行成本最小、备用成本最小和线路负载风险指标最小，如下所示。

F=min(F1,F2,F3)

(31)

(1)运行成本最小

运行成本F1包括常规机组运行成本C1，1、爬坡成本C1，2、启停成本C1，3。可削减负荷调度成本C1，4、可转移负荷调度成本C1，5和弃风成本C1，6，如下所示。

minF1=C1,1+C1,2+C1,3+C1,4+C1,5+C1,6

(32)

(33)

(2)备用成本最小

备用成本考虑机组的容量成本，如下所示。

(34)

(3)线路负载风险最小

(35)

3.2 约束条件

除前文提到的可削减负荷约束，式(5)～式(11)，可转移负荷约束，式(12)～式(15)外，还需要考虑的约束如下：

(1)网络潮流约束

(36)

(2)机会风险备用约束

(37)

(3)线路传输约束

(38)

式中：

(39)

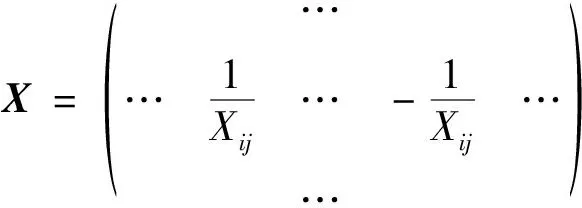
(40)

(4)其他约束

需要满足的其他约束有：机组爬坡约束、机组组合约束、机组启停约束、机组出力上下限约束、线路传输容量约束、风电出力约束等。

3.3 等价转换

式(36)～式(38)是由机会约束表示的约束条件，为了方便求解，由不确定规划理论[31]对其等价转换。

(1)网络潮流约束等价转换

当α>0.5时，式(36)等价于：

(41)

式(41)等价于：

(42)

式中：

(43)

(44)

λp-f=(λp-f,1,λp-f,2,λp-f,3)

(45)

λp,v=(λp,v,1,λp,v,2,λp,v,3)

(46)

λf-v=(λf-v,1,λf-v,2,λf-v,3)

(47)

(2)机会风险备用约束等价转换

当β>0.5时，式(37)等价于：

(48)

(3)线路传输约束等价转换

当γ>0.5时，式(38)等价于：

(49)

和

(50)

式(49)-式(50)等价于：

(51)

和

(52)

4 算例分析

4.1 算例设置与求解

本文采用改进的标准节点模型进行算例分析。峰-谷-平时段划分如表1所示。

表1 峰-平-谷时段划分情况

采用基于分解的多目标进化算法(MOEA/D)进行求解[32,33]。算法设置300个种群和200代有效进化次数。再用熵权法对求得的Pareto最优解集进行处理。MOEA/D将原多目标优化转化成若干个子问题进行求解，避免陷入局部最优，改善Pareto最优解集的均匀性。熵权法是一种客观赋权法，从信息熵的角度给出各个目标对最终结果的影响程度大小，以此确定各个目标的重要程度，即熵权。熵权越大，说明该目标对综合评估的影响越大，也越需要决策人员关注，为多目标问题的决策提供依据[34]。求解步骤如图3所示。

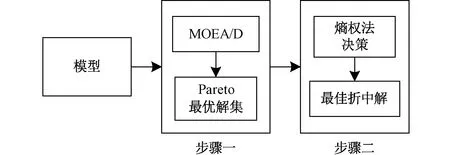
图3 模型求解步骤

算法设置300个种群和200代有效进化次数，主要细节如下：

(1)初始化种群

本文所提模型为非凸非线性多目标动态规划模型并具有混合整数特性。同时，在时序上有耦合关系的约束条件的约束性较强，如式(8)、式(9)等。为了避免进化算法退化为盲目随机搜索，在初始化种群时除了运用区域生成器生成种群外，还需要在种群进化开始前使得种群满足约束性较强的约束。对于不满足约束的种群则不会进入进化过程。

(2)约束条件处理

对于在进化算法开始前难以缩减的其他约束条件，采用可行性法则进行处理，在每一次进化后对不满足约束条件的种群按违反程度进行排序并剔除。若在某次进化中所有种群均违反可行性法则或找不到非支配种群，则本次进化不计为有效进化。

(3)其余算法细节与文献[33,34]保持一致。

4.2 不同情景的调度结果分析

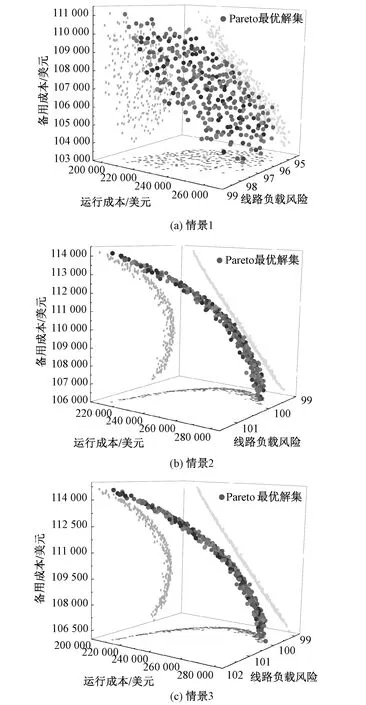
图4 三种情景的Pareto最优解集

为了更加方便的观察Pareto最优解集的分布情况，在图中还绘制了Pareto最优解集到各个目标函数平面的投影。从各个平面的投影可以看出，三种情景的Pareto最优解集的均匀性较好，说明MOEA/D算法在本文模型中的应用效果较好。在情景2中，只含价格型负荷。而价格型负荷的调用机制是用户根据电价特性自发的调节自身的用电行为。在优化过程中，不作为决策变量。机组的容量一部分作为运行成本，另一部分作为备用成本，而机组的运行成本是系统运行成本的主要组成，所以在情景2中，运行成本与备用成本具有线性相关关系。情景3同理。

采用熵权法列出综合得分最高种群的最优折中解，进行对比分析。三种情景的备用配置方式均采用2.1节中提出的机会风险备用。三种情景的求解结果如表2所示。

表2 三种情景的调度结果

由表2的结果可知：情景1相比情景2与情景3，在运行成本、备用成本和线路负载风险指标方面都有一定的改善。通过熵权的大小可以看出，情景1中，运行成本目标的熵权最大，说明决策者在情景1的设置中，应该把优化系统运行成本的目标放在第一位，其次可以考虑优化线路负载风险指标和备用成本。情景2相比情景3还考虑了价格型需求响应的作用，但价格型需求响应对于调度决策人员而言无法直接控制，情景2相当于在情景3的基础上从削峰填谷的方向对负荷曲线进行了修正，电网的灵活性不高，因此，在情景2和情景3中，线路负载风险指标的可优化空间不大。从其熵权的大小也可以得出这一结论。情景2和情景3的线路负载风险指标的熵权分别为0.136 7和0.151 8，低于各情景运行成本和备用成本的熵权。可见，在情景2和情景3中，调度决策人员应当重点关注运行成本和备用成本的优化。当配置可由调度直接控制的需求响应负荷时，除了可在运行成本和备用成本上得到优化外，还对降低线路负载风险指标，优化电网潮流分布有一定作用。

下面列出情景1的机组、柔性负荷等其他调度结果，进行详细说明。图5为调度的总体结果，图6为柔性负荷的调度结果。

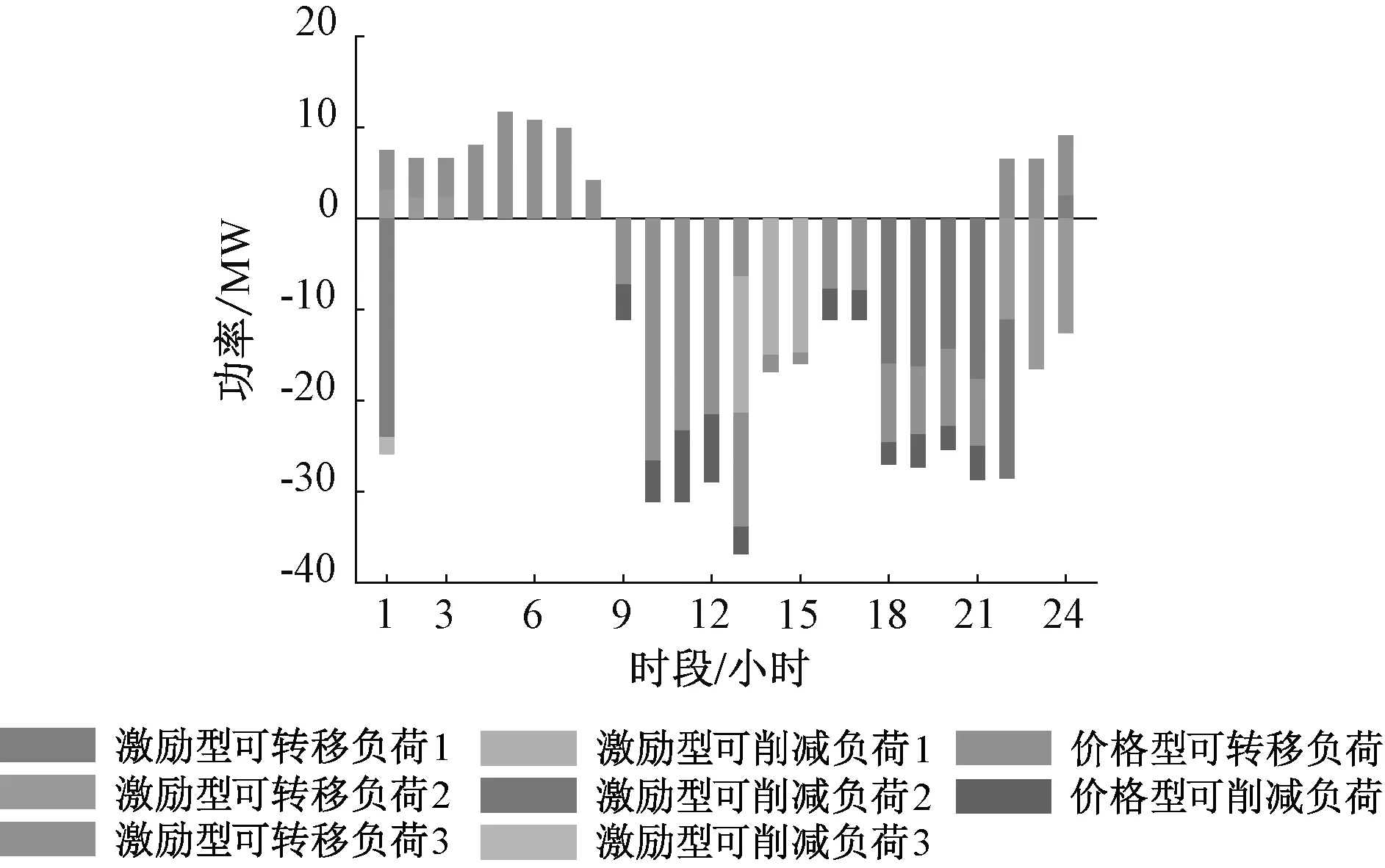
图6 柔性负荷调度结果

图5中，原始负荷曲线为不考虑需求响应的负荷曲线，对应情景3。从图5中可以看出，用电高峰的负荷曲线有所下降，用电低谷的负荷曲线有所上升，价格型需求响应和激励型需求响应均有削峰填谷的作用。在整个调度时间段上，降低峰谷差377.35 MW(9.89%)。价格型柔性负荷无额外约束，用户根据电价大小，自主选择自身用电行为，在整个时间段都有调用，将高电价时段用电转移到低电价时段或在高电价时段削减，由图6所示。其中激励型可转移负荷3为可平移负荷，将10:00～13:00的用电平移至负荷低谷04:00～07:00，其用电曲线在调度前后保持不变。结合表2和图5～图6的调度结果，可知，调度柔性负荷参与需求响应在优化运行成本、备用成本，减小线路负载风险指标，提高系统传输可靠性等方面具有一定的作用。

4.3 不同备用配置方式的对比分析

在情景1和情景2中，本节通过设置不同的备用方式，研究对各目标函数值和系统供用电可靠性的影响。

图7～图9以箱线图的形式绘制了不同备用配置方式下，各情景所有Pareto最优解集的结果和分布情况。图10以提琴图的形式绘制了不同备用配置方式下，各情景在所有调度时段内LOLP的结果范围和分布情况。

图7～图10横坐标的解释：1)“本文”指：采用2.1节中提出的考虑系统供用电可靠性的机会风险备用的配置方式；2)“无备用”指：备用容量的约束为0 MW；3)“+0%”指：备用容量为“系统中最大一台机组的容量+0%的负荷量”的配置方式，以此类推。当超过“+3%”的备用容量时，无可行解。

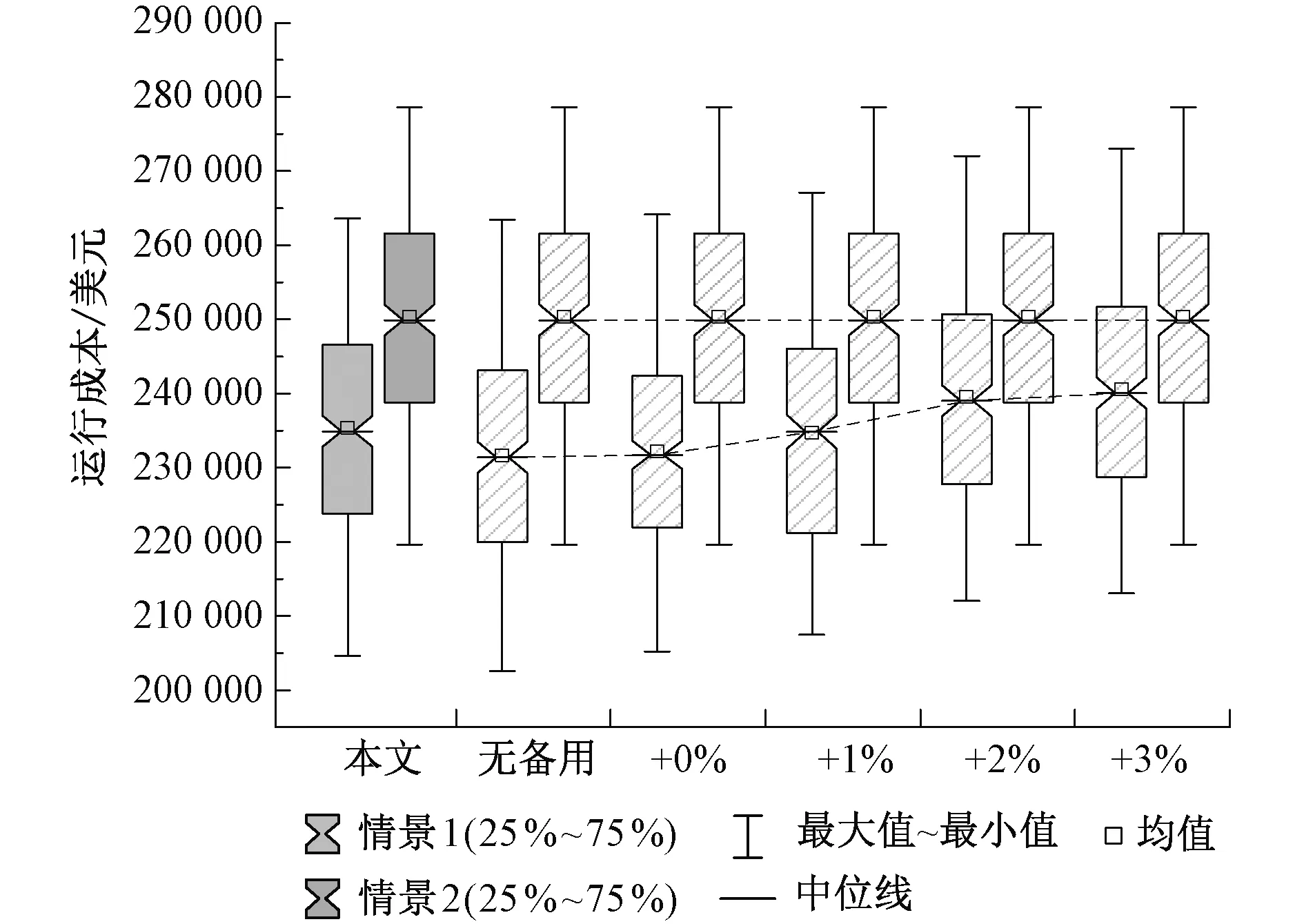
图7 不同备用配置方式下的运行成本

图8 不同备用配置方式下的备用成本

图9 不同备用配置方式下的线路负载风险指标

图10 不同备用配置方式下的系统电力不足概率

如图7～图8所示，各目标的中位线与均值基本重合，说明Pareto最优解集的分布性较好。客观起见，以各情景各目标值的中位线进行对比分析。

随备用配置容量的增加，情景1的运行成本、备用成本和线路负载风险指标均有所增加，而情景2的各目标值则基本保持不变。且情景1的各目标值均小于情景2的各目标值，以线路负载风险指标尤为显著。说明，对于不同的备用配置容量大小，调用柔性负荷参与需求响应可以对各目标产生优化作用。备用约束以“起作用约束”或“不起作用约束”的形式存在于模型中，情景2由于不含可由调度直接控制的柔性负荷，其灵活性较低。机组组合、风电出力等方式和结果相对固定，不会因为备用约束条件的改变而发生明显的变化，只有当备用约束条件由“不起作用约束”逐渐转变为“起作用约束”，并违反约束时，求解才会由可行解转为不可行解。说明柔性负荷调度可以提高电网调度的灵活性，适应不同的备用配置大小，优化各项指标。

如图10所示，“无备用”和“+0%”备用方式下，各时段的备用容量保持固定，分别为0 MW和223.3 MW，因此情景1和情景2的LOLP值和分布无明显区别。客观起见，对于“+1%”、“+2%”和“+3%”三种备用配置方式，以其最大值进行对比分析。随备用配置容量的增加，系统LOLP的值逐渐降低，且情景1的LOLP值小于情景2的LOLP值。“本文”与“+1%”的备用容量配置大小基本相当，从图7～图8中可以看出，各场景中各目标的值和分布也基本相同。而采用“本文”备用方式的情景1和情景2的LOLP值均为0.01，如图10中的表格所示。小于“+1%”备用配置方式下的0.010 480 57(情景1)和0.010 480 84(情景2)。当系统无备用配置时，失负荷概率为0.644 1，供用电可靠性水平较低，但采用“+0%”备用配置方式时，LOLP值显著降低，为0.030 446，说明在本算例中，当备用容量超过系统最大一台机组容量时，可将供用电可靠性提高到一定水平。

进而，可以通过提高备用容量，来获得更低的LOLP值，提高系统供用电可靠性，但需要额外损失一定的经济性。从图10可以看出，在“+1%”、“+2%”、“+3%”的备用配置方式中，LOLP值的下降虽然明显但数值较小。然而，从图7～图8中可以看出，成本的增加却是显著且较大的。

5 结 论

(1)本文对柔性负荷响应不确定性、刚性负荷不确定性和常规机组不确定性进行了建模分析。从传输可靠性的角度，优化线路负载风险指标。从供用电可靠性的角度，提出了考虑多重不确定因素的机会风险备用容量配置方法。

(2)本文以系统运行成本、备用成本和线路负载风险指标为目标函数，运用基于分解的多目标进化算法(MOEA/D)和熵权法进行求解和决策。

(3)本文考虑可靠性和源荷双侧不确定性，从经济性和可靠性的角度，研究了需求响应对运行成本、备用成本、线路负载风险指标和系统电力不足概率的影响。通过仿真算例和对比分析，需求响应在削峰填谷、优化运行成本、备用成本、降低线路负载风险指标、提高系统可靠性等方面具有一定的作用。