基于振动信号分析的有载分接开关故障诊断研究综述

赵书涛，王紫薇，胡经伟，李建坤，饶 燕

(1.华北电力大学 电气与电子工程学院，河北 保定 071003；2.国网湖北省电力有限公司 黄冈供电公司经济技术研究所，湖北 黄冈 438000)

0 引 言

变压器有载调压技术出现在上世纪90年代，依靠有载分接开关(on-load tap changer, OLTC)实现不停电调节电网电压。OLTC的电动机构、分接选择器和切换开关相互配合完成调压过程：电动机构通过槽轮驱动分接选择器预选到期望档位，同时驱动电机电流对弹簧机构输出稳定功率，储存一定能量后，释放能量带动切换开关动作。在变压器调压过程中对部件控制时序和可靠性要求极高，OLTC是唯一能频繁运动的部件，且长期处于高电压、大电流的恶劣环境下，出现滑档、转轴断裂、弹簧弱化、触头烧损等机械故障的可能性较大，据湖北电网统计，OLTC故障占有载调压变压器故障的20%，其中机械故障高达70%[1]，有载分接开关的状态监测和故障诊断技术已成为电气领域研究的热点问题。

目前对已投运的OLTC仍采用定期预防性试验、通过吊芯检修等离线方式进行维护，结合现场的间隔性巡视预防事故发生，但OLTC故障具有隐蔽性和突发性，在油室中不易观测和带电检测，容易造成“亡羊补牢”的事故后维修状态，浪费物力财力。因此，国内外学者已着眼于OLTC在线状态监测，寻找更适合及时发现设备早期缺陷的新方法。20世纪90年代ABB公司利用振动信号，在不拆开变压器外壳情况下对有载分接开关机械状态实现“听诊器”式检查，成为目前应用最广泛的监测与诊断方法。近几年OLTC运行故障的频发推动了故障诊断算法不断发展，本文在总结基于振动信号分析方法近期研究成果基础上，分析了振动信号处理的主流算法特点和局限性，探讨了目前研究中存在的人工特征提取困难、智能算法现场实用性不强等瓶颈问题，并对未来OLTC故障诊断方法及前景进行了展望，为基于振动信号处理的OLTC状态在线监测和故障诊断的实用化提供技术参考。

1 OLTC振动信号特征及预处理

1.1 振动信号波形特征

有载分接开关切换操作时，选择器与切换开关的撞击以及切换开关动静触头的相互碰撞，产生具有周期性的冲击信号，利用安装在变压器油箱顶盖或侧壁上的压电加速度传感器可获得伴随OLTC操作的原始信号[2]，如图1所示。

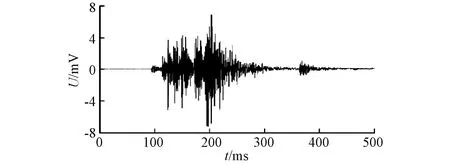
图1 原始振动信号

OLTC振动信号随机性较强，除一处冲击特征外无明显规律性变化，在弹簧疲劳、触头磨损等故障下，振动信号会发生畸变，提取信号特征可用于评估分接开关运行状态。考虑到OLTC机械结构复杂、现场工作电磁环境恶劣，在采集到原始信号后，需进行有针对性的信号预处理，通过对信号降噪和数据归一化处理，为数据特征提取和故障诊断奠定基础。

1.2 振动信号去噪方法

OLTC的振动信号包含有用信息的同时，夹杂电磁噪声、传感器自激振荡和随机振动的干扰，特征参数提取时首先需要解决有用信号被掩盖以及信噪比低的问题，目前OLTC振动信号降噪方法有维纳滤波去噪、小波去噪、变分模态分解去噪、及各种改进去噪算法等。

维纳滤波(Wiener Filtering)主要用于语音降噪，语音信号中会不可避免的受到来自外界环境的噪声干扰，严重影响识别率，需对信号进行预处理。文献[3]将该方法引入OLTC振动信号分析中，利用电机电流信号划分OLTC噪声段和带噪信号段，基于频谱特征构建维纳滤波器，降噪效果见图2。

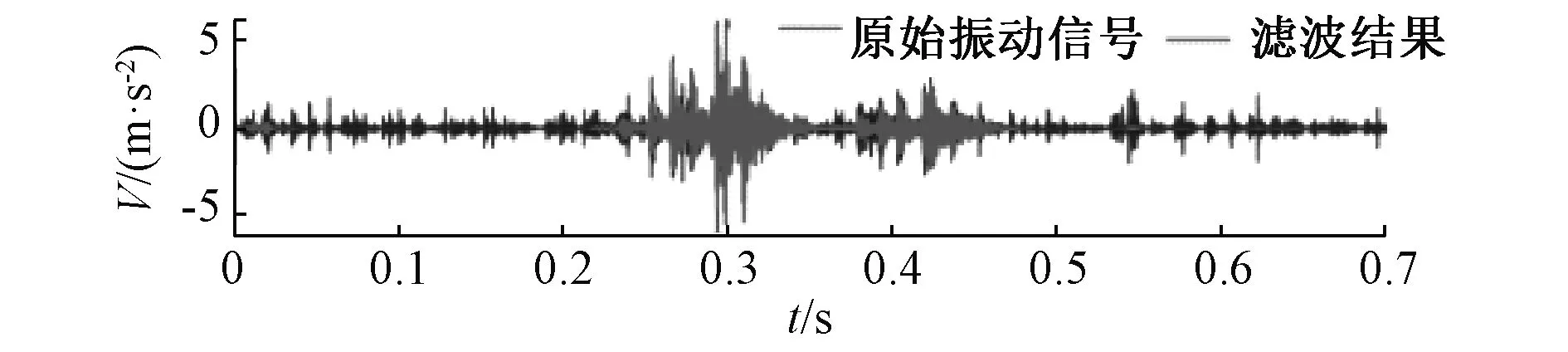
图2 维纳降噪效果图

小波去噪主要有小波阈值法和基于模极大值法。小波阈值法去噪性能过于依赖阈值的选取，但胜于计算速度较快、软阈值滤波得到的信号平滑，在使用时需把握住抑制噪声和保护图像细节之间的动态平衡。基于模极大值法的特殊之处在于可根据奇异点性质对信号进行滤波，能有效的保留奇异点信息。对于阈值法来说，常用的阈值选取方式有固定阈值、无偏风险估计阈值、启发式阈值和极大极小阈值[4]。因OLTC振动信号具有短时性，且信噪比低，一般采用固定阈值就可满足去噪需求，如文献[2]。文献[5]基于模极大值Adhoc算法[6]可很好的抑制随机噪声和高频成分，原因在于OLTC振动信号中含有较多奇异点，去噪性能虽好，但计算速度慢，相较于小波阈值法慢数十倍。

变分模态分解(Variational Mode Decomposition, VMD)克服了经验模态分解中模态混叠现象，且相较于小波分析，VMD自适应性及鲁棒性更强。文献[7]提出VMD与小波包阈值降噪相结合的算法，但对未考虑VMD参数k和α的选取，降噪效果不佳。文献[8]利用人工鱼群仿生算法(AFSA)可快速确定最优参数k和α，图3为优化后的VMD算法与经验模态分解算法降噪对比图，证实VMD算法的优越性。

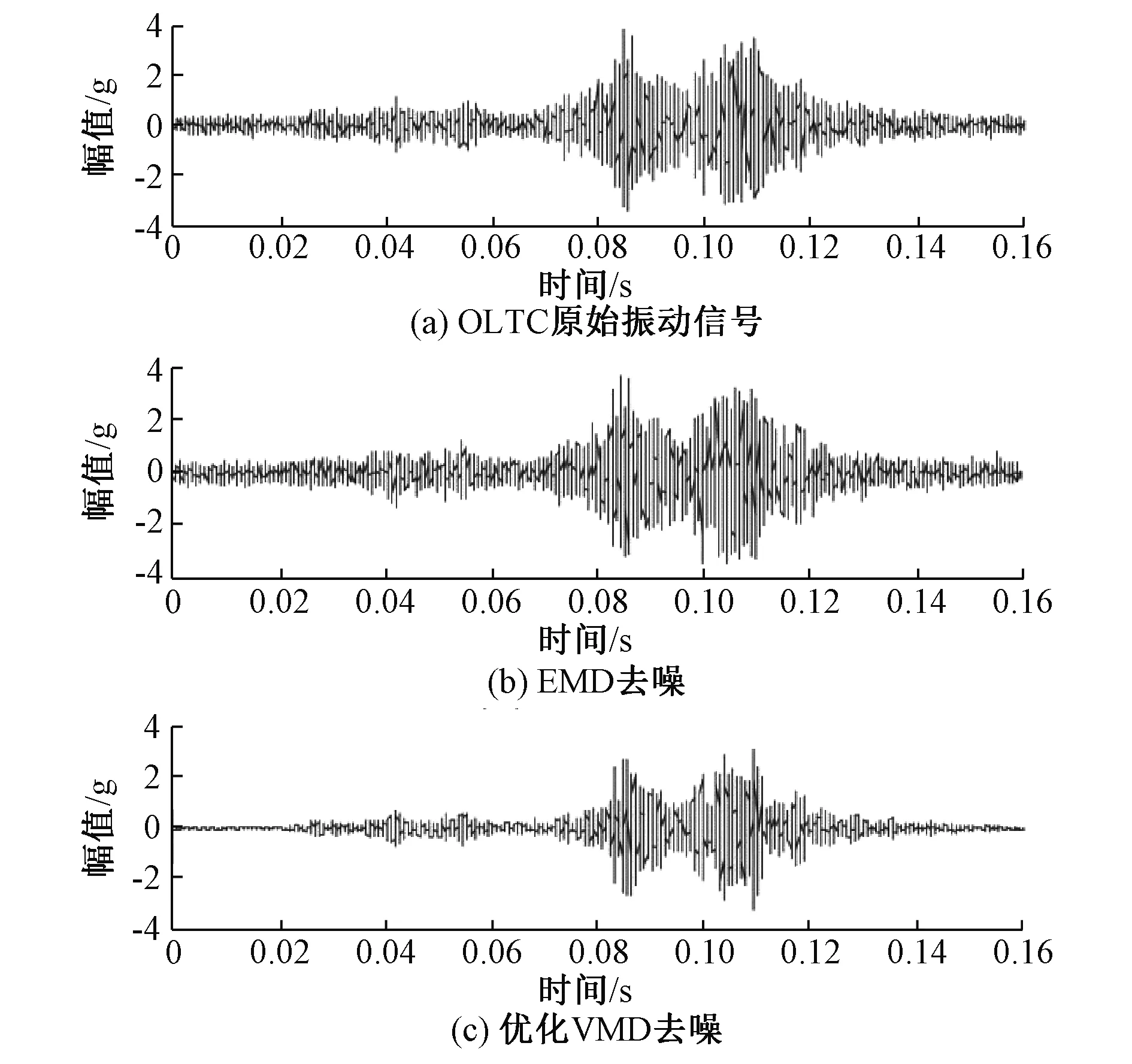
图3 EMD算法与优化VMD算法效果对比

经验模态分解降噪、VMD降噪等算法均使用先分解、后构造的思想，去除噪声段IMF分量，再将剩余分量重构得提纯信号。此外，去噪方法还包括小波包分解降噪[7]、奇异值分解降噪[9]、局部均值分解[10]等。

1.3 数据归一化处理

在OLTC在线监测及故障诊断技术中，振动信号必须进行数据归一化处理，一是消除特征指标间量纲的影响，二是将数据限定在期望的范围内。不仅方便计算、提升模型收敛速度和算法精度，而且能够防止基于深度学习故障诊断的模型梯度爆炸[11]。

文献[12,13]通过振动数据进行归一化处理，使各传感器所测数据间具有可比性；文献[14,15]实现了特征熵、排列熵等模态分量的归一化处理，将提取出的特征数据映射在一定范围内。归一化方式主要有(0,1)归一化和Z-score归一化，分别如式(1)和(2)所示：

(1)

(2)

式中：μ为原始数据均值；σ为原始数据标准差。

其中(0,1)归一化因在实际运算中，其最大值和最小值不稳定，导致归一化结果也不稳定，该方法只适合数值较为集中的情况[15]。当需要距离来度量相似性，则Z-score归一化更为适合，诸如OLTC故障的分类、聚类、相空间重构等算法[5,14,16]。

2 振动信号的特征提取方法

2.1 传统小波变换和经验模态分解

不同工况下振动原始信号差异甚微，特征提取目的在于放大特征差异，将原始特征转化为具有物理意义的特征量，便于状态的识别与分类。小波变换和经验模态分解(empirical mode decomposition，EMD)是常用的特征提取方法，小波变换作为多分辨率数字显微镜，是假设振动为分段平稳信号，可利用时域多尺度缩放特性，绘出二维小波系数的“垂直脊线图”来评估OLTC状态[17]。文献[5]基于小波变换各尺度的模极大值来计算信号奇异性指数，以此来判别OLTC的动静头表面状况，并得出结论：有载分接开关触头磨损、触头弹簧松动时，波峰奇异性指数α变大；触头烧损时α变小。

EMD常与Hilbert变换相结合，即将EMD分解后的信号做Hilbert变换，可获得三维时频幅值谱图，能精准反映幅值随时间和频率的变化[18]，如图4所示，其右侧纵坐标表示幅值大小，该方法又被称之为希尔伯特-黄变换(Hilbert-Huang Transform, HHT)。此外，EMD的能量熵也常用于OLTC特征提取[19]，基于公式(3)可分辨出触头正常与烧毁曲线差异，但其数学计算过程中需要用到三次样条插值，计算更为复杂，耗时较多。

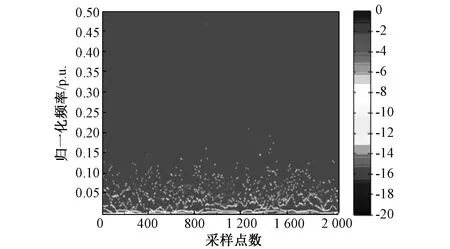
图4 OLTC故障信号三维时频谱图

(3)

式中:Ei是第i个IMF分量的能量，E是完整信号总能量。

2.2 基于传统算法的改进方法

随着小波变换算法的发展出现了小波包分析(wavelet packet analysis)、第二代小波变换、复小波和球面小波等，OLTC振动信号处理目前主要以小波包分解为主。小波包分解相较于传统小波变换，进一步对高频信号进行划分,可自适应的选择相应频带，提高信号分辨率。文献[14,15]应用了小波包总能量诊断算法和小波包特征熵诊断算法，针对触头故障，发现了明显特征信号。从原理上来说，OLTC振动信号因包含信息太过复杂，传统小波变换直接摒弃掉高频分量容易丢失价值信息，导致提取特征量不够精准，小波包分解更适用于OLTC振动信号的联合时频分析。

传统EMD算法有以下缺点：①当数据不是纯白噪声时，会发生模态混叠现象，导致某些IMF分量时频分布失真；②直接摒弃部分IMF分量进行简化计算，可能造成真实信息的丢失，对诊断结果产生偏差；③所提取特征参量物理意义薄弱，与OLTC动作时序相关性不强。针对这些缺点，众多学者在EMD算法上做出不同改进。集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)通过在目标信号中加入白噪声序列，使其均匀分布在整个时频空间,有效解决了EMD算法模态混叠的缺陷。文献[20]将EEMD用于OLTC故障诊断中，实现了对触头松动故障的检测，但同时，为减少结果中残留的噪声信号，EEMD算法需大量的集总平均次数，计算量显著增加，且存在添加噪声的随机性强的缺陷。文献[21]提出互补集总经验模态分解法(Complementary Ensemble Empirical Mode Decom-position, CEEMD)，该方法中白噪声残留量与集总平均次数无关，有效解决了文献[20]的短板。文献[22]对CEEMD分解后的IMF分量进行时频矩阵划分，利用Teager能量算子法提取时频域划分线、时域峭度、时频矩阵变异系数等特征参量。文献[16]提出窄带噪声辅助多元EMD法(Narrowband Noise Assisted MEMD,NNA-MEMD)，其思想与EEMD类似，但相比于EEMD添加噪声的随机性，该算法使主频率部分得到集中加强和放大，准确性进一步提高。

2.3 混沌理论分析

机械振动受各种因素影响，在振动序列中包含不同程度的混沌现象，伴随非线性、非平稳、不规则等特征。区别于传统时频分析算法，有学者从混沌动力学角度研究对OLTC振动信号进行分析。

(1)相空间重构：文献[23]利用相空间重构混沌分析，基于虚拟仪器研制出OLTC振动测试系统，将一维时间序列重构成高维非线性动力系统，并计算最大Lyapunov指数，均为正数，指明了该系统具有混沌特性，如图5所示。文献[24,25]根据Takens嵌入定理[26]，定义了相点空间分布系数(Phase Point Distribution Coefficient, PPDC)作为相轨图的几何特征参数：

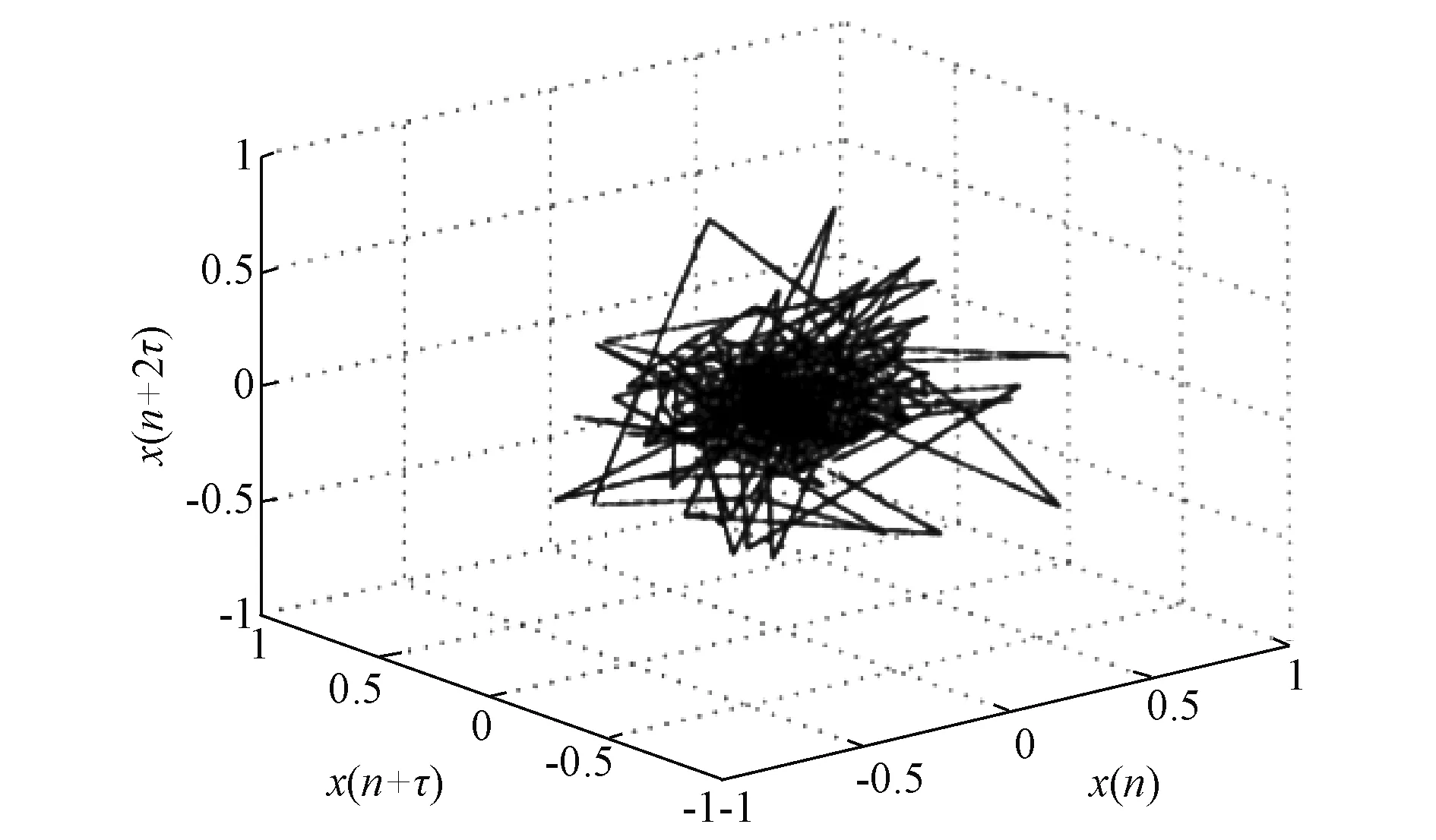
图5 振动信号相空间重构图

(4)

式中：Rm为平均几何距离；Ra为吸引子半径。

通过现场试验数据得出：当PPDC数值保持相对稳定时，OLTC相对稳定；一旦PPDC数值发生较大变动，表示OLTC机械运行状态可能发生异常。

PPDC虽可在一定程度上描述不同振动模式下的特征变化，但其并未考虑到重构信号的矢量特性，对故障识别能力有限。

针对这一缺陷，文献[27]利用多变量相空间重构(Multivariate Phase Space Reconstruction, MPSR)对OLTC多通道的振动信号进行处理，根据Bayes估计和奇异值分解提取特征信息，与文献[24,25]相比，弥补针对单一测点处振动信号分析不全面的缺陷,进一步提高了OLTC特征提取的准确性。

(2)相空间递归定量分析：文献[28]在相空间重构的基础上，运用了递归图定量分析法来判别故障信息，其具有小数据、抗噪能力强等优势，将递归行为展现在二维平面上，引入递归率(recurrence rate, RR)、层流性(laminarity, LAM)和确定性(determinism, DET)指标来描述振动信号的特性，指明了OLTC从正常状态过渡到故障状态必然伴随着RR降低、DET和LAM增大的趋势。但该算法依赖于递归阈值ε的选取，若选取不当，会直接影响特征提取效果。

文献[29]在RP递归图上做出改进，提出距离映射递归图(Distance Mapping Recurrence Plot,DMRP)，将不同相点间的距离映射到递归图的像素点颜色信息，避免了ε的选取难题，具有更强的特征刻画能力，自适应力更强，两种算法的对比如图6所示。

图6 OLTC的RP与DMRP算法对比

2.4 特征提取方法评价

小波变换计算速度最快，但精确度主要由小波基函数和分解层数决定，文献[30]引入了Parseval’s理论计算相关系数，确定了最适合于OLTC振动信号研究的母小波，为bior3.3。因此，小波变换可用于对时间要求高的在线监测中，选用bior3.3为母小波也可满足精度需求。经验模态分解的IMF分量可自适应的分析信号中主要成分，避免人为强制给定基函数，相比而言，EMD虽然耗时较多，但在分析非平稳信号、滤波降噪精度上具有更大优势。

混沌理论分析作为机械振动信号处理的另一分支，区别于传统时频分析法，从崭新的角度探索OLTC机械振动信号的动力学特征，该方法可绕过构建精确的数学模型，直接将一维时间序列重构成多维相轨图来提取特征，弥补了时频分析法建模困难的问题，为OLTC振动特征提取技术开辟了一个新的方向。

3 智能化故障诊断方法剖析

提取出振动信号特征量后对比实际工况，可初步判别OLTC是否处于故障状态，但尚不能进一步准确区分故障类型。随着人工智能技术深入发展，机器学习和深度学习方法被引入到OLTC诊断中，提高了OLTC故障智能诊断的技术水平。

3.1 传统机器学习

传统机器学习中监督学习(supervised learning)按照人为给定输入输出,对训练样本给出“标签”，，通过已知答案训练得最优模型；而非监督学习(unsupervised learning)的训练样本中不含“标签”，未知样本答案，根据给定数据集挖掘内在结构。

(1)监督学习

(a)决策树：决策树是一种预测模型，表示对象属性与值之间的映射关系，可对分类做到直观、清晰。文献[31]提出一种基于决策树的OLTC振动信号综合分析法，采用二叉树模型进行分层推理，适用于故障种类繁多、具有同类模型的识别诊断。

(b)支持向量机：支持向量机(Support Vector Machine, SVM)结构简单，主要利用径向基(RBF)核函数技术，搜索最优惩罚因子C和BRF参数γ。文献[32]阐述了SVM核心参数(C和γ)对算法泛化能力的影响，并采用遗传算法(Genetic Algorithm, GA)对参数进行优化，对主弹簧断裂和主触头松动两类故障的准确率达86.7%。文献[15]构建二叉树支持向量机，模型如图7，模拟传动机构滑档、主触头松动、主弹簧松动和传动机构卡涩四类故障，提取150个小波包能量熵为样本，训练发现二叉树支持向量机在区分传动机构类故障时误诊率较高，测试样本准确率为86%。

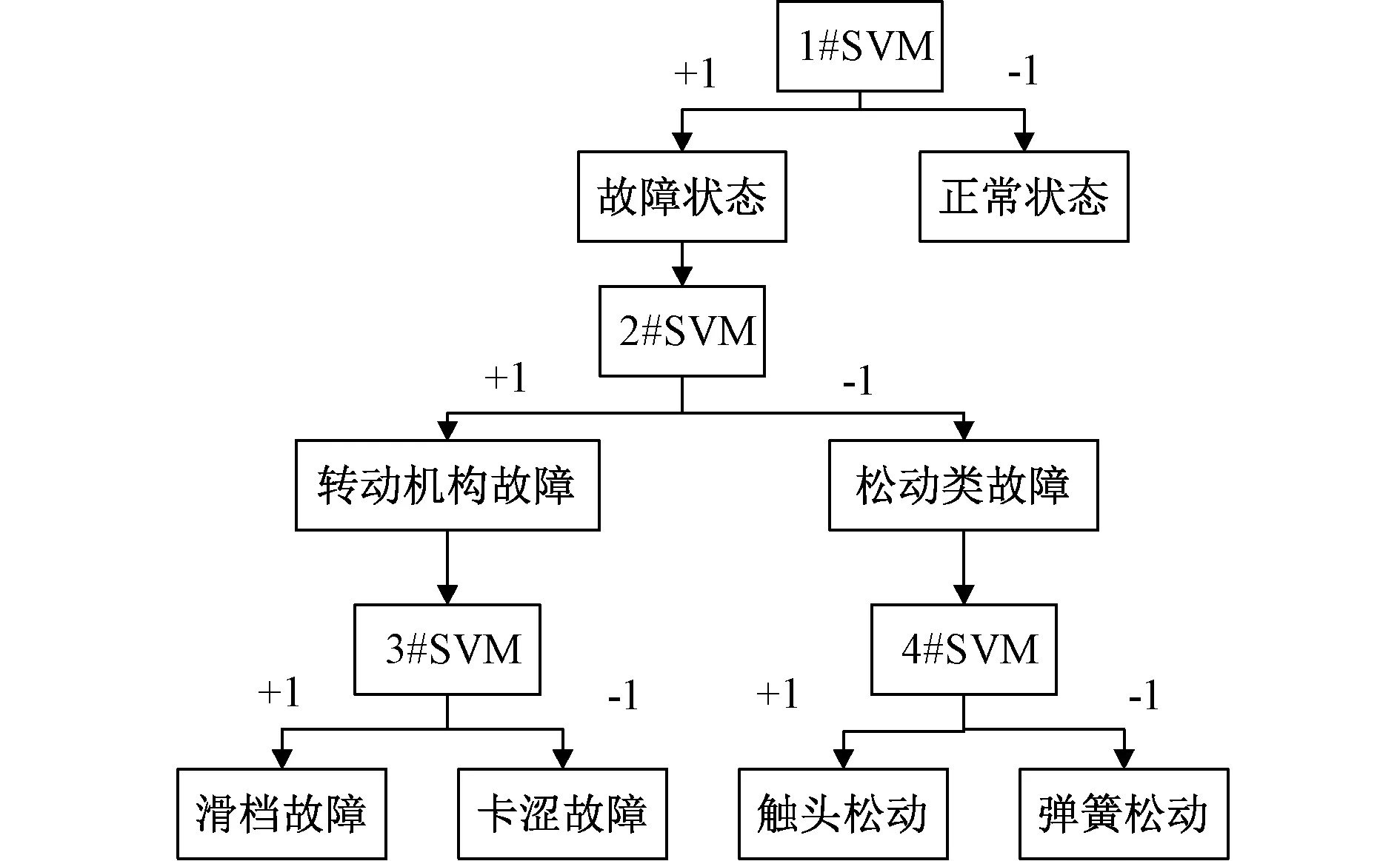
图7 二叉树支持向量机模型

文献[33]采用最小二乘支持向量机(Least Squares Support Vector Machines, LS-SVM)，用等式约束代替不等式约束，避免了传统SVM中二次规划问题，提高诊断效率。文献[12]对粒子群(PSO)算法做出改进，优化惯性权值ω和学习因子c1、c2，使SVM尽可能跳出局部极小值，全局搜索SVM最优参数。文献[34]采用模拟退火优化支持向量机，训练得最优模型C=0.25、γ=4，对弹簧和触头不同程度的故障综合诊断率可达95.83%，但轻微程度类故障的误判率较高。

(2)非监督学习

典型的非监督学习为聚类分析，常见算法包括K-均值(K-medoids)、层次聚类、隐马尔可夫模型(Hidden Markov Model, HMM)、自组织映射等。目前文献中应用于OLTC的算法主要以K-means聚类为主。

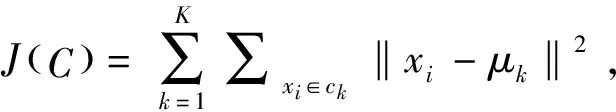
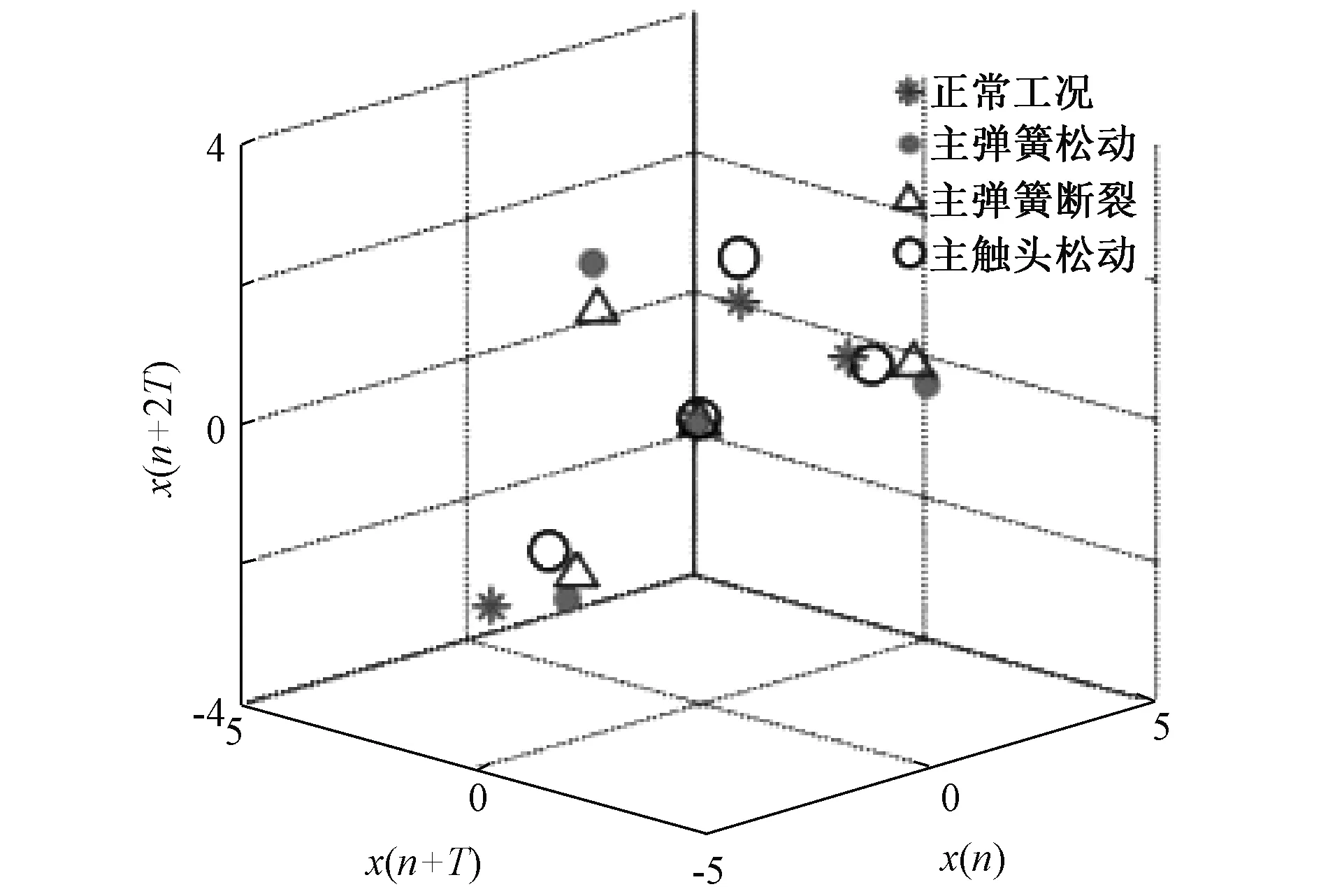
图8 簇中心相空间位置

K-means缺点为对初始值群的个数与位置要求苛刻，需事先设置类别数，不同初始值对结果波动影响较大，且在非凸数集中难以收敛。基于此，文献[36,37]对K-means做出不同程度的优化，分别引入PSO和层次聚类算法确定初始聚类中心参数值，其中文献[37]采用K-means++改进算法[38]，J(C)仅取决于簇的个数，进一步提高算法精度。

除上述算法外，文献[22]提出以局部异常因子(Local outlier factor, LOF)算法，通过对数据点密度，可准确识别出OLTC弹簧松动、弹簧疲劳和弹簧断裂三种不同程度的故障，详见图9。

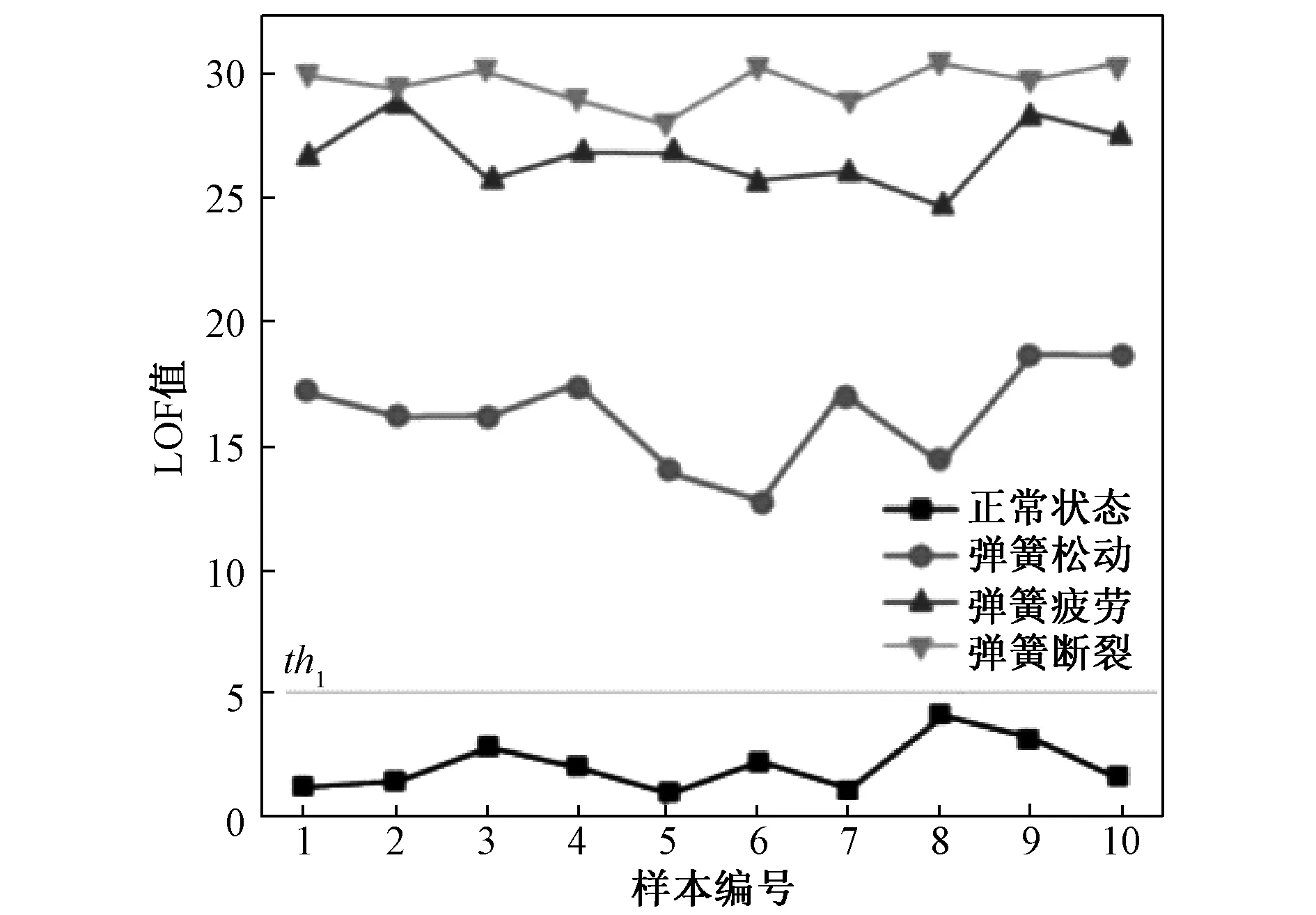
图9 本体故障与正常时LOF值对比

传统机器学习优点是结构简单、易实现、鲁棒性较好，其中SVM在小样本训练中优势较为突出，K-means聚类适用于处理分接开关数据量大的情况。缺点主要包括：①需人工提取特征信息，抗干扰能力差，易受环境因素影响；②对算法初始参数值敏感，需配合各种优化算法才能发挥其优势；③OLTC故障种类繁多，上述算法中对故障分类均不够细致。

3.2 深度学习

深度学习相较传统的机器学习，其学习能力更强、适应性更好，但计算量普遍偏大，对计算机硬件的要求更高。

(1)优化BP算法：反向误差传播算法(Back Propagation, BP)基于梯度下降算法，具有较好非线性与容错性，广泛运用于OLTC故障诊断中。但其缺点明显：① 对初值要求敏感，训练易陷入局部极小值；②隐层数目和节点数目依靠先前经验，结构难以确定；③收敛速度较慢，泛化能力难以保证。

针对BP神经网络缺陷，文献[12,39]采用自适应遗传算法(Adaptive Genetic Algorithm, AGA)来优化网络输入层、隐含层的权值ωs，隐含层、输出层的权值ω0，隐含层神经元阈值θ和输出层神经元阈值γ，采用浮点编码对参数进行修正，AGA优化前后的识别精度如图10，其中文献[39]对主弹簧弱化、主轴变形、触头松动和磨损的识别精度高达96.68%。

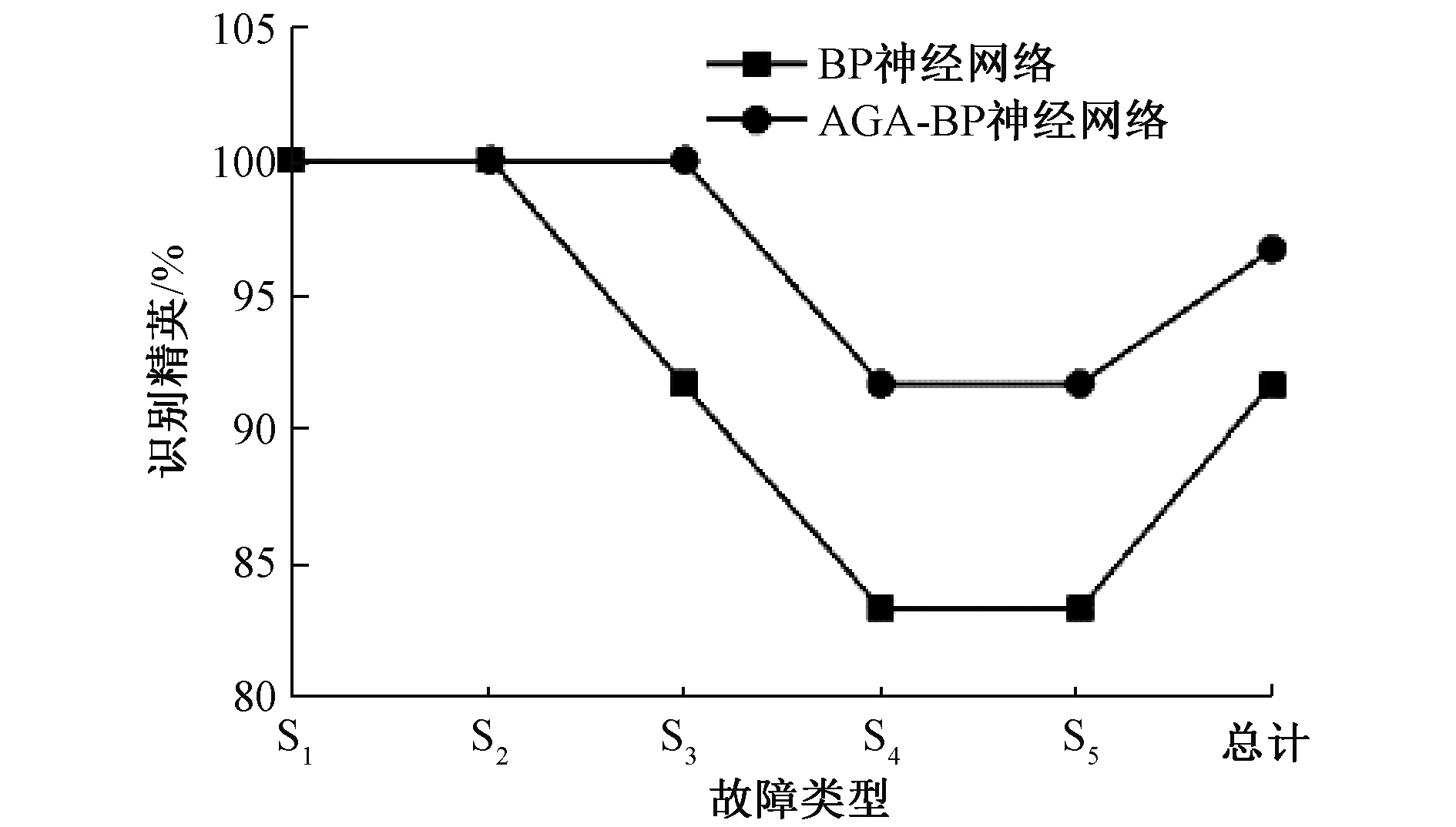
图10 AGA-BP算法与BP算法识别精度对比

极限学习机(Extreme Learning Machine, ELM)被视为BP的改进算法，通过随机生成隐含层节点的权重提高学习效率，增强泛化能力[40，41]。文献[42]借助模拟退火(Simulated Annealing, SA)算法，对ELM隐含层节点失效进行优化，提高模型分类精度，试验模拟弹簧和触头的典型故障，测试准确率也可达96%。

(2)卷积神经网络：卷积神经网络(Convolutional Neural Network, CNN)在电力行业尤其是OLTC故障识别方面仅起步阶段。文献[29]首次将CNN引入到OLTC机械故障诊断中，以输入递归图为训练样本，训练得到最优模型为：5×5卷积核、网络层数为7。故障识别准确率见表1，相较于其他算法，触头磨损故障准确率至少提升10%。

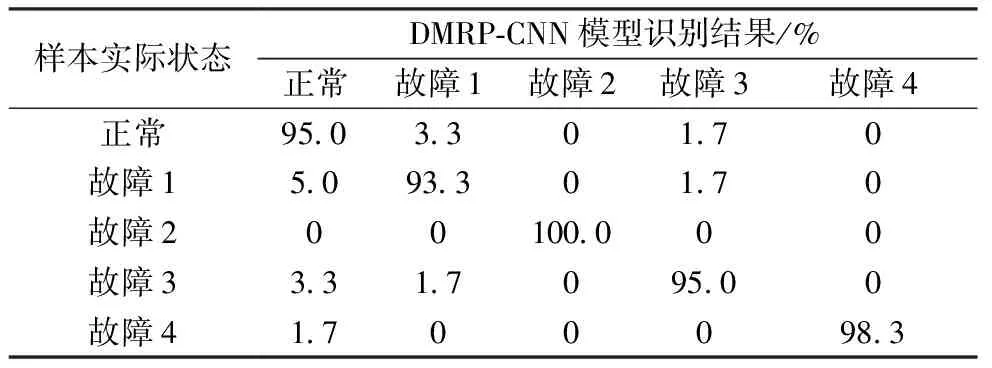
表1 CNN模型识别准确率

表中：故障1、2、3、4分别为连接推杆变形、连接推杆断裂、过渡触头轻微磨损和过渡触头严重磨损。

深度学习相较于传统机器学习，学习能力更强，网络层次多，适应性能较好，可解决较多复杂的问题，且准确率高。但存在如下缺点：①计算量大、对硬件要求高，因此成本较高；②模型设计难度较大，目前用于OLTC的神经网络的现成模型具有一定局限性；③深度学习需基于大数据训练，而OLTC故障数据却很少，需长时间的现场试验数据累计，所以其研究发展较慢，现阶段适用于处理大规模训练样本数据的试验平台中。

4 技术瓶颈分析及展望

综上所述，有载分接开关的在线监测技术有声波、电流和振动等多种方法，虽以振动信号为基准的发展最为迅猛，但其技术手段均有各自优势和局限性，在数据数量和数学方法上仍有较大瓶颈。

(1)数据提纯难度较大、特征的最优提取算法匮乏。数据质量直接奠定模型泛化能力及识别精度，而OLTC作为机械与电气相结合的部件，产生的信号极为复杂，原始数据中包含的因素杂乱，加大了特征提纯的难度。在现有研究中，大多文献仅着眼于降噪处理，此外还应注意数据是否存在离群点和缺失值。特征提取以小波包分解、IMF分解和相空间重构为主，但均存在相应缺陷，且准确率与计算量不可兼得，如何平衡两者关系是未来发展中重要一环，还需寻找更适合非线性、非平稳振动信号的数学手段。

(2)故障诊断技术发展不够成熟。在传统机器学习中，无论是支持向量机还是聚类分析，对弹簧轻微故障和触头松动误判率较高，如文献[15]和文献[34,35]。究其原因是这两类故障振动信号特征极为相似，人工提取特征信息困难。深度学习是近几年该领域研究热潮，但需大量数据累计才能使准确率升高。在确保计算时间的基础上，从传统机器学习方法中去其糟粕、取其精华，发展一个收敛性好、泛化能力强、计算成本低、可基于小样本训练的深度学习新方法是接下来研究重点。

(3)单一特征量诊断效果不全面。OLTC故障类型较多，在前述文献中，所做研究基本以开关切换类故障为主，除此之外，还有开关滑档故障、工作失调故障和密封箱漏油等，单一的特征量与OLTC众多故障不能做到一一对应关系。文献[43]率先将旋转角度信号运用到在线监测中，文献[44]在此基础上进行改进，以旋转角、振动和电机电流信号三者相结合，为OLTC多方面状态感知奠定基础，进一步提高在线监测实用性与准确性。在未来工作中，尝试挖掘除旋转角度及振动之外的监测手段，深入研究OLTC的声、振、电和姿态等多信号监测和融合分析技术，为电网的可靠调压发挥重要作用。

(4)在成熟应用层面研究不足。目前，关于OLTC故障诊断算法虽多，但大多停留在算法理论研究和技术仿真阶段，未真正运用到实际现场中，在恶劣工作环境下，设备抗电磁干扰能力和滤除杂波等问题不容小觑。今后，在一段时间内应考虑着重发展现场测试，开发适合于现场实际运行的成套监测设备，累计大量实验数据，及时更新、丰富数据库，加强数集融合的研究，将高效、科学的人工智能引入到变压器有载分接开关状态评估中，提升现场监测和检修的实用化水平。

5 结 论

用于电网带载调压的OLTC机构复杂、运行故障多种多样，目前的故障监测研究方兴未艾。本文从数据预处理、特征提取和故障诊断三个方面，对基于振动信号的有载分接开关状态监测技术进行回顾，重点研究了多种非平稳振动信号特征提取算法，并详细对比了故障诊断中传统机器学习和深入学习的优劣。

(1)现阶段OLTC故障诊断领域虽取得了一定成果，但应用于工程实践中还远远不够，研究多局限于区别单一故障，当同时出现两种或以上故障时，振动信号表现的不仅仅是直接叠加，在辨识算法上有巨大研究空间。

(2)从提升诊断准确率角度建议综合驱动电机电流、旋转角度、声音和温度等多路信号进行深入分析，在相当长一段时间内应继续完善信号测试的基础数据库，集中完成对OLTC运行故障样本的大量累积。

(3)随着深度学习算法日益成熟，在保证计算时间和成本的大前提下，尝试优化基于小样本数据的训练，挖掘更多故障类型与特征的对应关系，从实用化角度提升算法辨识准确度和实用性。