基于162台超、特高压变压器的声纹特征预警阈值划定研究

刘云鹏，王博闻，周旭东，罗世豪，刘嘉硕

(华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003)

0 引 言

超、特高压电力变压器作为电网的核心设备，对大范围电网的安全稳定运行具有重要影响[1]。为保障特高压变压器的安全稳定运行，已有许多不停电检测技术应用于到变压器中。其中，变压器的声纹检测技术由于传感装置无需与变压器之间产生电磁耦合且能够对变压器的整体性机械故障进行检测与诊断，因此在变压器的在线监测、不停电检测等工作中具有很强的优势。

变压器在运行过程铁芯、绕组等结构会发生振动并产生机械波，产生的振动和声音信号包含了大量的设备状态信息。由于变压器的振动信号和声音信号相比具有更强的抗干扰能力，因此目前关于变压器的状态监测研究多集中在振动信号的研究，但是振动信号采集对于布点位置的要求更为严格，较小的布点偏移将导致测量结果产生很大的变化[2]，这不利于不同型号变压器振动数据统一化，而声音传感器的小幅位置偏移后接收到的信号则不会产生较大差异，使得声纹诊断法在人工巡检中具有一定优势。

对于变压器声纹诊断方法，主要分为机器学习方法与特征值诊断方法[3，4]。以深度学习为代表的机器学习方法具备更强大的特征学习能力，可以从大量样本的数据集中训练出更强大的模型，能够从原始输入数据中抽象出其本质。但此类方法的可解释性弱，不利于辅助运维人员决策，且通常需要较为完备的样本类型和较平衡的数据样本才能得到可商用的成熟模型。近两年来，国内变压器声纹监测项目方兴未艾，但未来一段时间内故障样本尚不能支撑深度学习模型商用落地。因此，需要在积累数据样本的同时，围绕声纹特征值诊断方法展开研究。

声波与振动波同属机械波，声信号起源于振动信号，当机械波从振源传播到空气中即呈现为声信号，因此在声信号的研究中一般会从其振动源头出发进行机理性分析。目前，已有需对专家学者从机理分析与实验模拟角度，针对变压器异常状态下的声振特征值研究：汲胜昌、师愉航等人构建了两体物理模型对变压器绕组多倍频振动特性进行了理论解释并提出半频率比特征量[5，6]。王丰华等人从绕组垫片力学非线性角度给出了振动特性中出现高次信号现象的理论解释，指出不同绕组松动程度与振动信号中100 Hz倍频分量之间的关联关系[7]。吴晓文对实验室中的变压器的进行了不同负载状态下A计权声压级测量[8]。马宏忠等人认为基频是判断变压器机械状态的重要特征[9]。祝丽花等人对直流偏磁下铁心搭迭区域的振动特征进行描述[10]。何金良等人对于500 kV直流偏磁的声信号进行分析[11]。上述理论研究对变压器各状态下可能出现的频率现象进行了单独的分析，为声音及振动信号分析提供了大量分析判断依据，具有重要参考价值。然而，领域内学者的研究样本大部分基于实验室模拟平台，针对现场数据的分析数量较少，对于各种特征指标在现场应用时预警的阈值比较模糊，亟需在大量数据统计的基础上进行预警阈值划定。

为获得可靠明确的声纹预警阈值，课题组首先针对国网河北省电力有限公司管辖的162台500 kV超高压、1 000 kV特高压单相变压器展开现场声纹采集工作；其次，使用幅值相角波动性法去除风机干扰噪声，排除统计样本的干扰因素；然后，围绕五项特征值展开数据统计分析，给出正常运行中的超特高压变压器声纹特征值分布规律；最后，根据统计结果，给予特征值预警阈值建议，并应用2例现场实测变压器故障或异常声纹样本对预警阈值进行测试，证明其应用可靠性。该预警阈值划定方法能简单有效地挖掘正常数据样本的价值，不必受制于故障样本稀缺的条件限制，短期内即可积累大量样本，因此具备一定的实用价值。

1 500 kV变压器声纹样本库采集

1.1 样本库变压器类型分布

课题组针对国网河北省电力有限公司管辖的500 kV、1 000 kV超、特高压变压器展开现场声纹采集工作(不含换流变压器)。由于变压器全部为三相分体式变压器，每相的变压器可认为是一台单相变压器，状态相对独立，因此本文以单相变压器作为样本个体进行统计分析。样本变压器属地、冷却方式、生产厂家分别如表1、表2、表3所示(部分变压器为多种冷却方式相结合，能够根据不同负荷进行调节，表2中按照其满负荷运行状态下的冷却方式进行统计)。

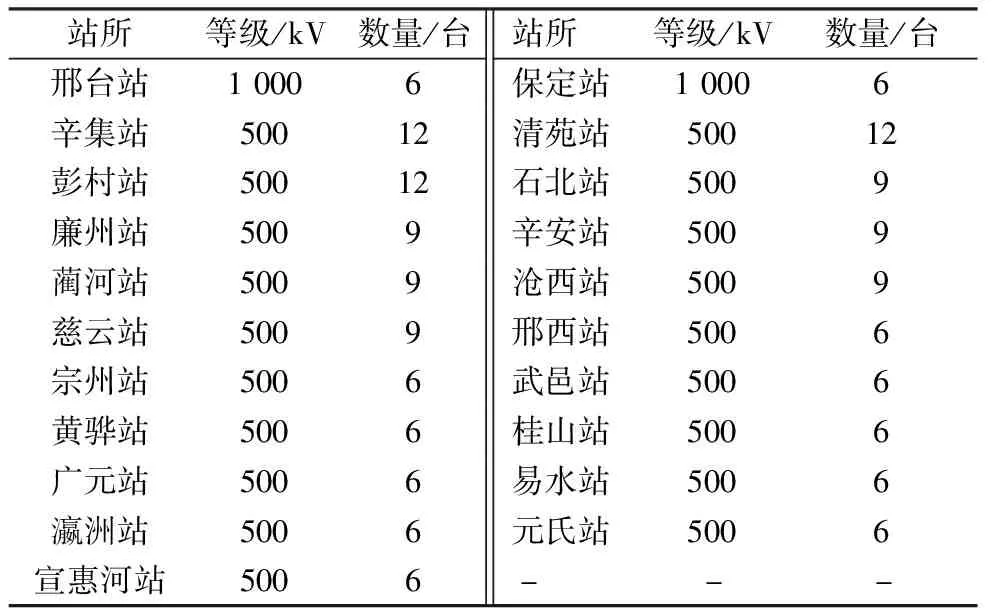
表1 声纹样本库变压器所属站所分布

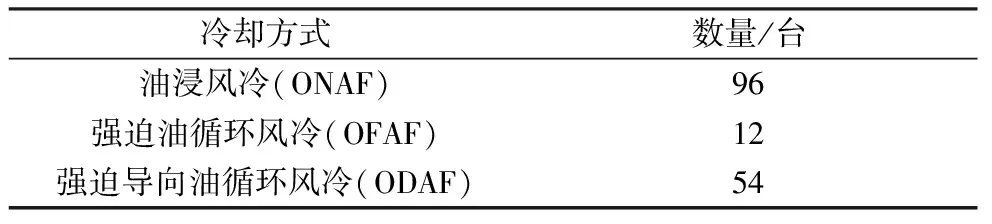
表2 声纹样本库变压器冷却方式

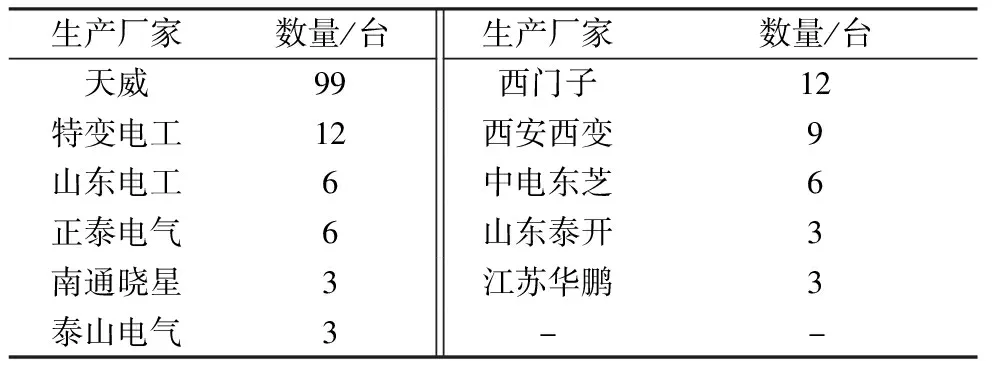
表3 声纹样本库变压器生产厂家

样本涵盖3类冷却方式、10个生产厂家、21个站所的162台变压器。变压器均处于正常运行状态，负荷率均在30%～50%之间，采集现场已对梯子等异响附件进行了消噪处理，排除了无关干扰声源。样本库涵盖的超、特高压变压器型号多样，类型丰富，能够支撑声纹特征统计结果的可靠性。

1.2 声纹测量系统及传感器布置原则

在声纹采集装置方面，根据IEC 61672[12]标准，噪声测量频率范围应覆盖25 Hz～16 kHz，采集设备采用驻极电容枪式指向型麦克风与录机的组合系统以确保记录数据的可靠性：枪式指向型麦克风具有较强的指向性，频率响应范围满足采样要求；录机具有24 bit 96 kHz记录能力，其高频率响应与宽动态范围能够记录尽可能多的噪声细节，保证了数据的准确性。

在采集装置布置方式方面，麦克风布置位置遵循以下原则：(1)避开冷却器所在端面；(2)尽量设置在长端面侧；(3)垂直对准绕组，对于单相变压器而言，布置于端面居中位置;(4)麦克风指向方向垂直于变压器表面非加强筋位置;(5)距变压器油箱壁水平距离以不超过麦克风最大量程为准，一般选取50～150 cm之间，本文采集均选择布置于100 cm处;(6)距地面垂直距离150 cm。

2 风机干扰噪声的去噪处理

变压器声信号采集过程中会不可避免的收集到瞬态干扰和稳态干扰，由于变压器本体声纹稳定持续，因此在计算声纹特征时可以通过避开存在瞬态干扰片段的方式避免该类干扰，然而超特高压大型变压器上普遍配置有风冷系统，风机噪声作为稳态干扰，不可避免地会混合进信号中，因此在进行特征分析前应首先对声纹开展风机噪声剔除工作。

2.1 幅值相角波动性判别法去风机噪声方法

本文应用幅值相角波动性判别法[13]消除风机噪声与背景噪声。该方法围绕声纹样本信号短时傅里叶变换后各频点的幅值与相角随时间的波动性来区分变压器本体频点和风机噪声频点。根据以上2个维度的波动特性，将得到2个变压器本体声纹主导的频率点集合，取两者的交集形成最终的变压器本体声纹主导的频率点集合，其他的频点即认为是风机或环境噪声的频率点集合。最后，将快速傅里叶变换后的风机噪声频率点在混合信号中进行谱减，即可得到变压器本体的频谱分布，方法计算流程如图2所示。

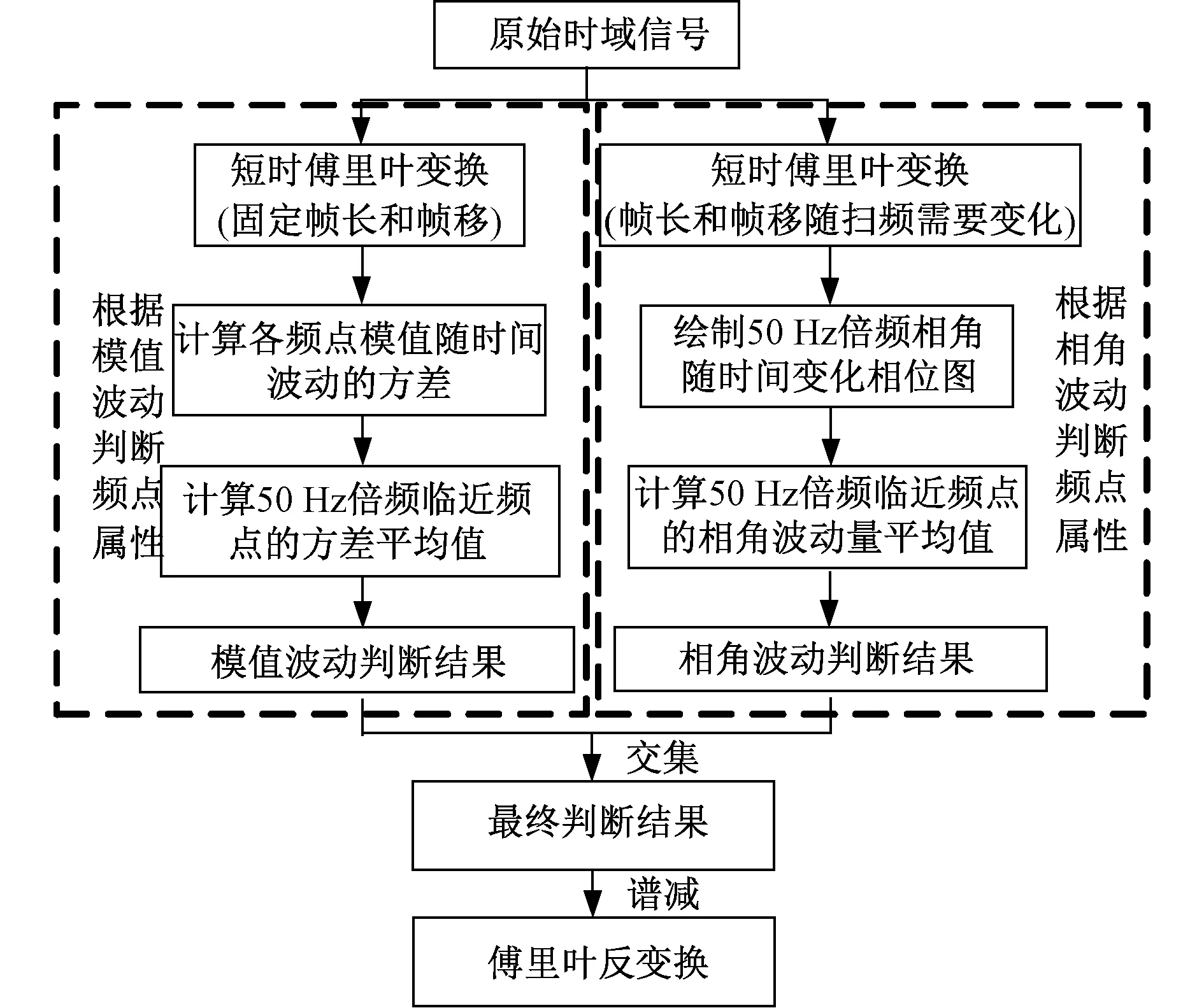
图2 幅值相角波动性判别法去风机噪声步骤

(1)幅值波动性计算过程中，50 Hz倍频临近频点的方差平均值ak计算公式如式(1)所示：

(1)

式中:δf为频率f的方差，k为正整数；w为频点临近区域范围，一般取10。若δf>ak即判定频率f为干扰频点。

(2)相角波动性计算过程中，50 Hz倍频临近频点的相角波动量平均值bk计算公式如式(2)所示：

(2)

式中：ηf为频率f的相角波动量，由短时傅里叶变换第i帧算得的相角在幅值为1时的复数zi计算得到，计算公式如式(3)所示，式中：pf为声纹样本在计算频率f时分帧的数量，由帧长、帧移和样本长度决定，帧长为10/f，帧移为1/f。

(3)

若ηf>bk即判定频率f为干扰频点。

2.2 幅值相角波动性去噪算例

根据幅值相角波动性法，本文对162台500 kV、1 000 kV超、特高压变压器中部分风机噪声干扰较大的样本进行去噪处理。由于篇幅有限，此处仅列出邢台站2号主变A相的去噪结果。图3与图4分别为幅值波动与相角波动的判断结果，被判定为干扰信号的50 Hz倍频点被圈出。

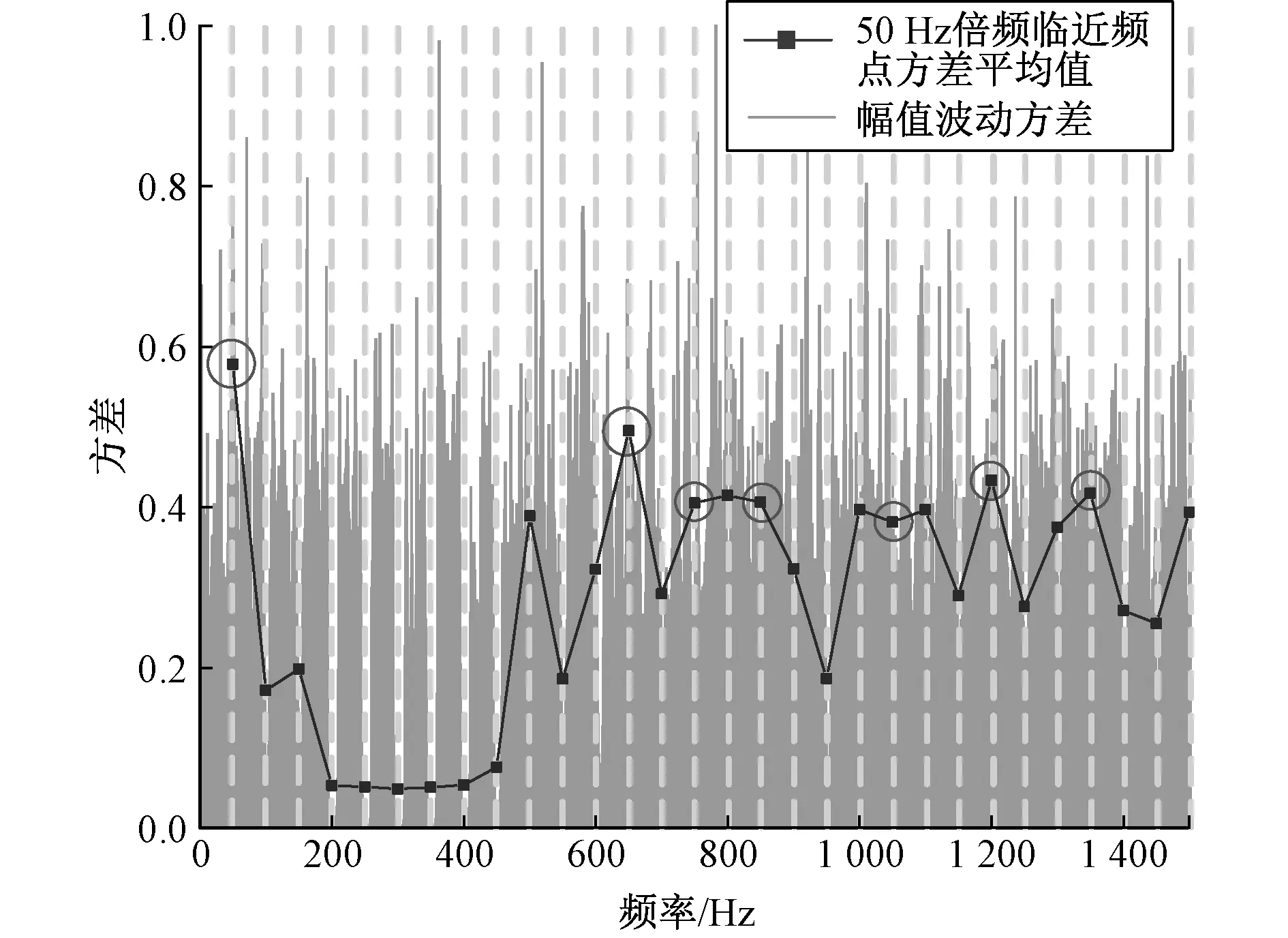
图3 幅值波动判断结果

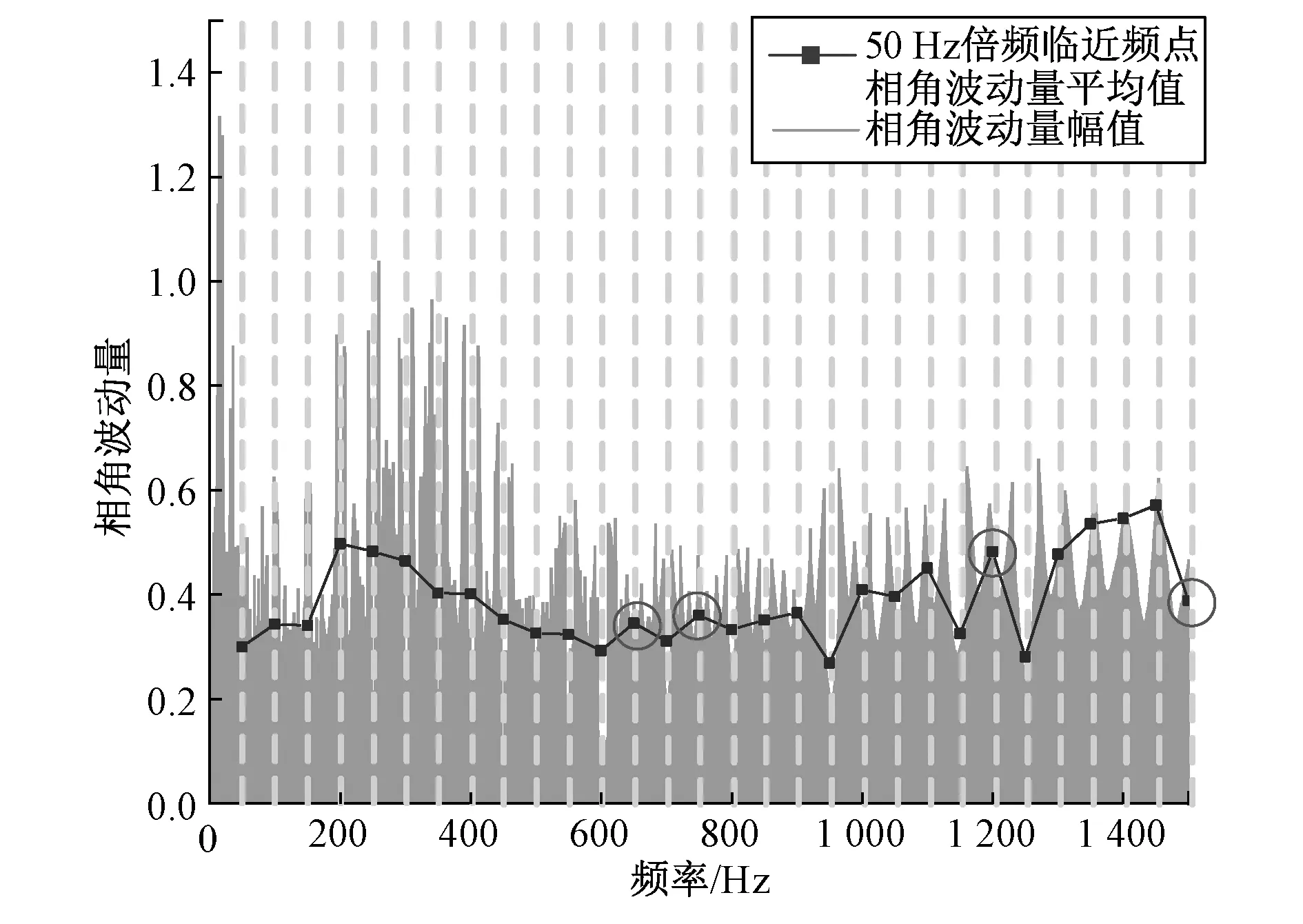
图4 相角波动判断结果

谱减法去除红圈标记的频点后，进行傅里叶逆变换即可得到去噪后声纹样本。去噪前后频谱对比如图5所示。

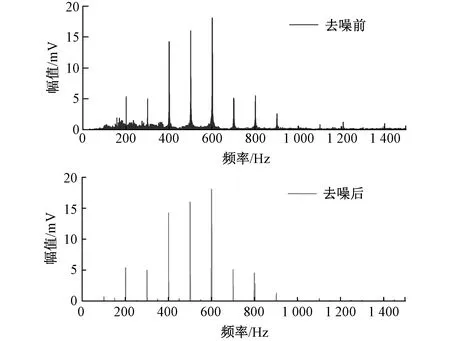
图5 变压器本体与风机噪声分离结果

3 变压器声纹特征筛选

变压器本体声纹可分为瞬态声纹与稳态声纹。瞬态声纹主要是指变压器遭受短路冲击瞬间的声纹，除了此之外，变压器声纹在绝大多数情况下都是相对平稳的稳态声纹。本文主要围绕变压器的稳态声纹的特征进行分析研究。

3.1 变压器声纹案例时域信号与频域分布

以某500 kV变电站1号主变为例，变压器正常运行时声纹时域和频域信号如图6所示。

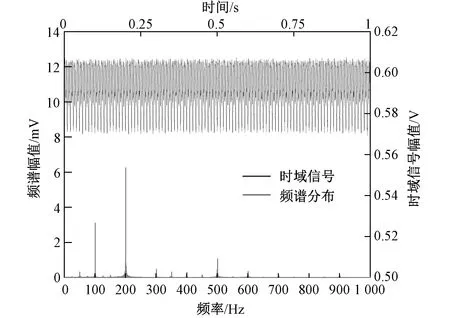
图6 变压器正常运行时声纹的时域信号与频域分布图

当变压器出现异常状态时，变压器的声纹信号在时域或频域上都将发生一定变化。如图7所示为两例现场实测得到的变压器异常状态案例。例一为某500 kV变压器直流偏磁状态，例二为某220 kV变压器垫块松动。可以看出，例一和例二的声纹时域信号和频谱分布都差异。相较于直接使用时域信息，声纹的频域信息能够一定程度对信号进行压缩，且对频谱分布特征差异更为显著。因此，本文主要对变压器声纹的频域特征进行梳理和分析，筛选出最具代表性、能反映故障信息的特征量，为后文的数据统计的提供依据。

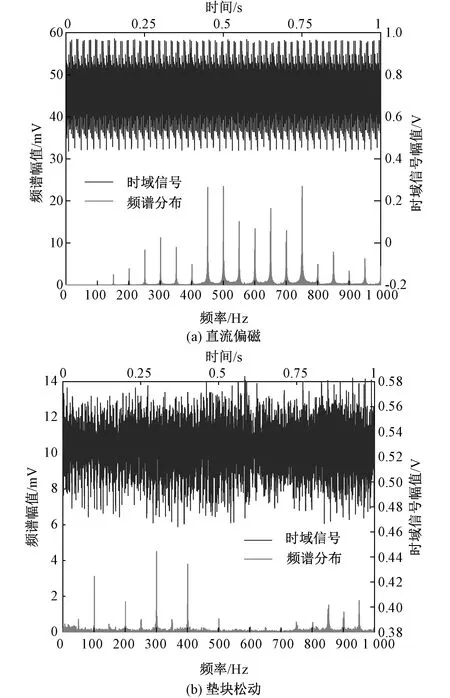
图7 变压器异常状态时声纹的时域信号与频域分布图

3.2 频域特征筛选

变压器常规声纹的频域特征主要有：频域幅值最大值、幅值最小值、幅值中位数、幅值平均值、幅值峰峰值、主频、振动熵、50 Hz奇偶次倍频比、主频比重、基频比重、总谐波畸变率、高低频比、高频比重共13个特征。具体表达式如表4所示，表中：Xf为振动信号在频率f处的频率分量幅值；N为统计的频率上限，由于变压器声信号能量主要分布在0～2 000 Hz范围内，因此N一般取2 000 Hz；argmaxXf为频率分量最大时的频率fHz；Xf为Xf2/(X1002+X2002+…+X20002)；fh为高低频分界频点，一般取700 Hz。

本文围绕表4中的13个特征值，分别进行分析筛选：

(1)出由于不同变压器本身机械结构、传感器布点位置等因素都会对采集到的声纹幅值产生影响，因此本文认为跟声纹的幅值相关的特征值只能作为单台变压器长期固定监测时的相对参考，对于不同变压器之间的横向对比没有太大意义，因此本文对表4特征指标中的频域幅值最大值、频域幅值最小值、频域幅值峰峰值、频域幅值平均值、频域幅值中位数均不做深入分析；

表4 频域特征值及其计算表达式

(2)主频：变压器本体声纹主频通常不会有较大变化，一般为50 Hz的偶次倍频。当变压器机械结构或电磁激励出现变化时，声纹将发生主频转移或主频变为50 Hz奇次倍频；

(3)振动熵：振动熵能够描述变压器声纹50Hz倍频的含量分散程度，当变压器绕组变形或机械松动时，振动熵将升高；

(4)50 Hz奇偶次倍频比：当变压器处于直流偏磁状态时，铁心发生故障都会导致50 Hz奇次倍频上升；

(5)主频比重：文献[14]分析了变压器主频比重，但变压器主频受机械结构或电磁激励影响，在变压器发生机械故障时主频会发生转移，此时主频比重的计算对象也随之转移，因此主频比重这一特征值对变压器状态分析并无明确意义，本文不做深入分析；

(6)基频比重：变压器铁心及绕组振动基频为100 Hz，在实际运行中铁心和绕组受到谐波、形变、松动等因素干扰导致振动信号中增加了其他频点。因此针对基频比重的监测能够反映外界干扰因素变化状况，对变压器状态监测具有一定意义；

(7)总谐波畸变率：总谐波畸变率与基频比重的特征核心意义相同，两者大致互为倒数的关系，因此本文仅选取基频比重展开分析；

(8)高低频比：当变压器发生铁心、绕组机械松动或处于直流偏磁状态时，变压器声纹高低频比会上升；

(9)高频比重：高频比重与高低频比的特征核心意义相同，因此本文仅选高低频比展开分析。

4 变压器声纹典型特征预警阈值统计分析

根据上一章的分析结果，本文最终选择主频、振动熵、50 Hz奇偶次倍频比、基频比重、高低频比五项典型特征值进行预警阈值分析。首先通过对各特征值进行特征分布计算，确定特征是否呈现聚集性，然后根据特征值计算原理分别确定其上限或下限为预警阈值，最后使用实际案例进行有效性验证，若声纹的某项或某几项特征超过阈值即可判断为状态异常。

4.1 特征分布分析

(1)主频:如图8(a)所示为变压器声纹主频分布直方图，从图中可以看出，变压器声纹集中分布在100 Hz、200 Hz等50 Hz的偶数频点上。由累积概率曲线可知，仅有1例样本在100 Hz到400 Hz之外，绝大部分数据集中在100 Hz到400 Hz之间。

(2)振动熵:如图8(b)所示为变压器声纹振动熵分布直方图，从图中可以看出，变压器振动熵集中分布在1.0至1.7之间。由累积概率曲线可知，99%的样本在1.7以下。

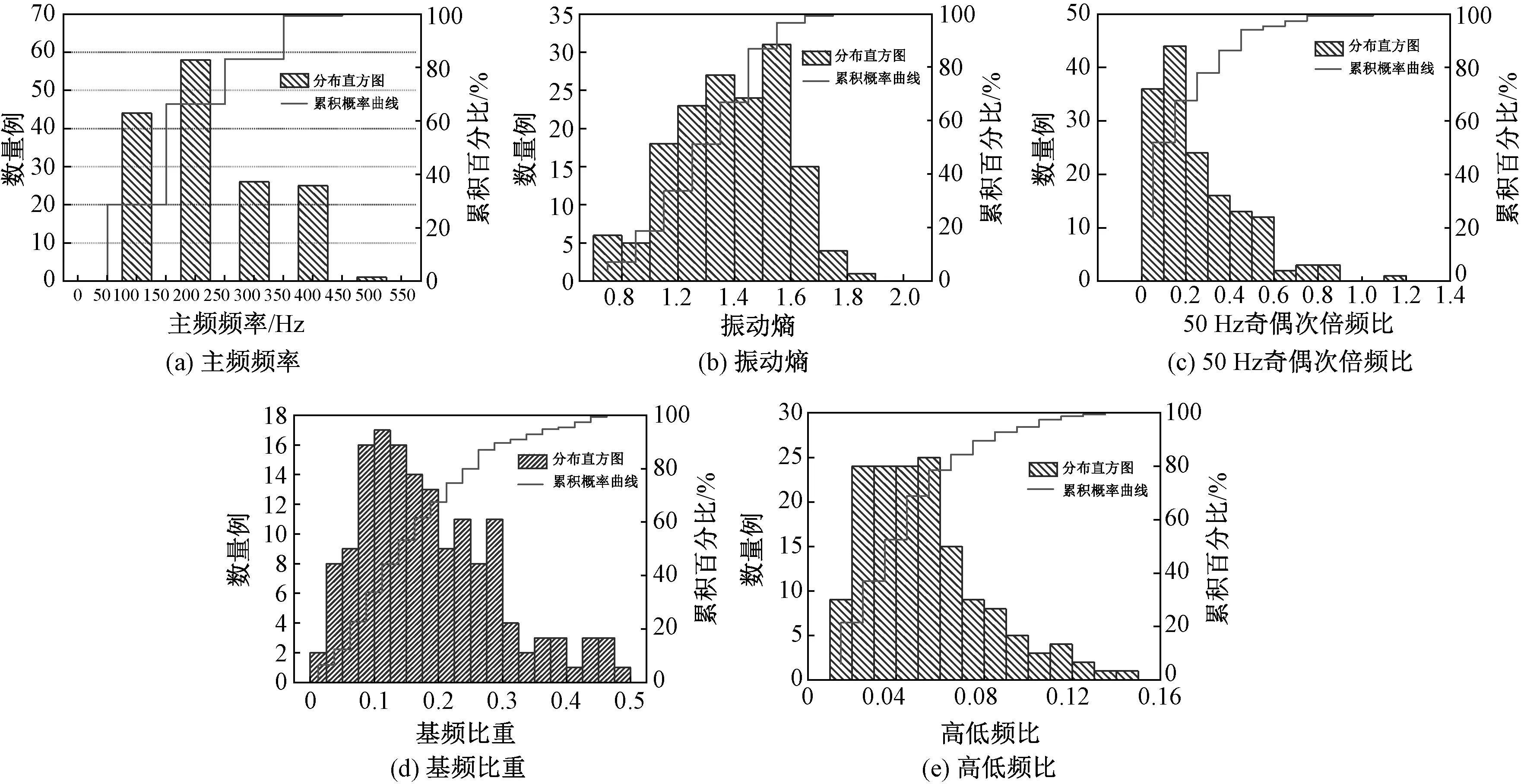
图8 变压器声纹典型特征分布直方图与累积概率曲线

(3)50 Hz奇偶次倍频比:如图8(c)所示为变压器声纹50 Hz奇偶次倍频比分布直方图，从图中可以看出，变压器振动熵集中分布在0至0.6之间。由累积概率曲线可知，99%的样本在0.9以下。

(4)基频比重:如图8(d)所示为变压器声纹基频比重分布直方图，从图中可以看出，变压器基频比重集中分布在0.025至0.3之间。由累积概率曲线可知，99%的样本在0.025以上。

(5)高低频比:如图8(e)所示为变压器声纹高低频比分布直方图，从图中可以看出，变压器高低频比集中分布在0.01至0.08之间。由累积概率曲线可知，99%的样本在0.14以下。

由图8可知，除振动熵符合正态分布以外，其他特征均呈现右偏态，符合对数正态分布规律。按各特征值的分布状态绘制概率图如图9所示，各图中数据点均沿参考线均匀排布，验证了表5中各特征值分布状态的合理性，具体的分布参数如表5所示。

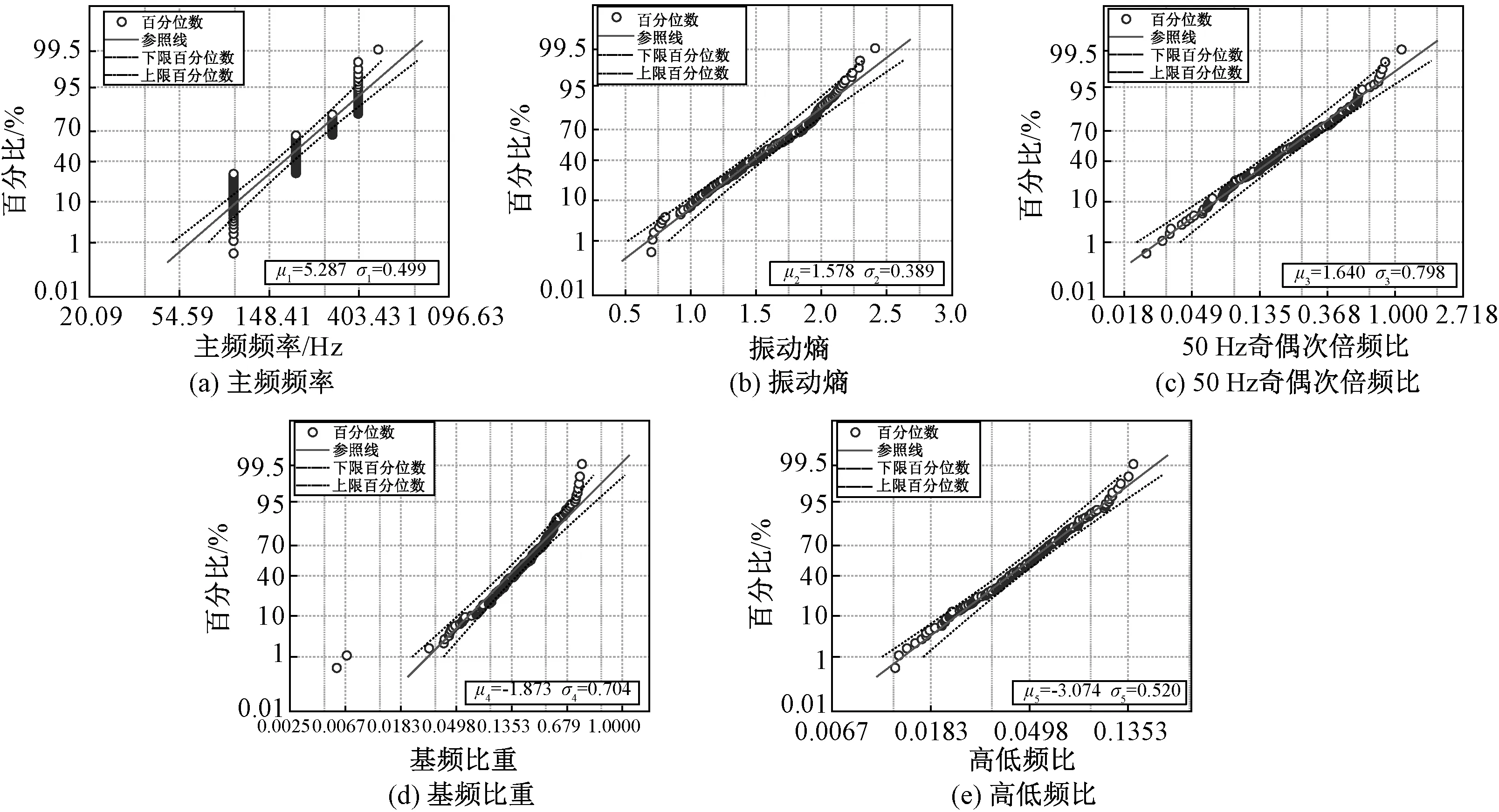
图9 变压器声纹典型特征正态/对数正态概率图

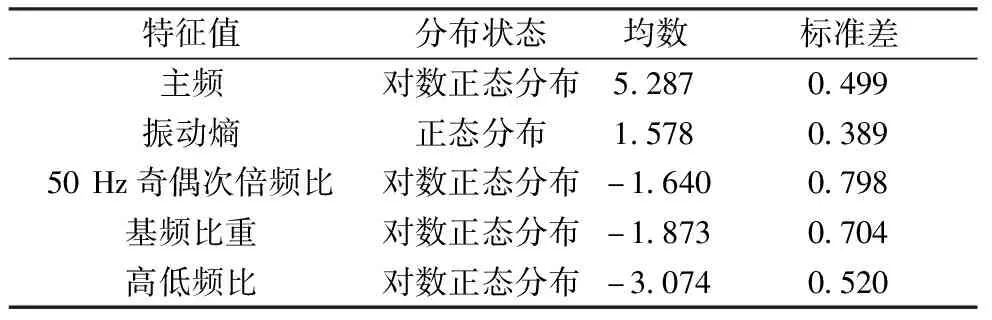
表5 特征值分布状态与分布参数

4.2 典型特征值预警阈值

根据上节分析可知，5项典型特征值都服从正态分布或对数正态分布，具有很强的聚集性，具备阈值预警方法的分布特性基础，可以设置特征值的上分位线或下分位线为预警阈值，用于变压器异常状态检测。

(1)主频: 当变压器处于直流偏磁时，主频会向高次频点转移，需要关注主频分布的上限。为排除少量异常值，选取99%分位线作为主频预警阈值，本文样本数据集得到的主频上限预警阈值为400 Hz；

(2)振动熵: 变压器绕组变形或机械松动时，振动熵将升高，即振动熵与变压器异常概率成正比，因此需要关注分布的上限。为排除少量异常值，选取99%分位线作为振动熵警戒阈值。本文样本数据集得到的振动熵上限预警阈值为2.3；

(3)50 Hz奇偶次倍频比: 变压器直流偏磁会使主频向50 Hz奇次倍频点转移，需要关注50 Hz奇偶次倍频比的分布上限。为排除少量异常值，选取99%分位线作为50 Hz奇偶次倍频比预警阈值，本文样本数据集得到的50 Hz奇偶次倍频比上限预警阈值为0.852；

(4)基频比重: 变压器的谐波、漏磁、形变、松动等因素干扰会导致振动信号中增加了其他频点，使基频比重下降，因此需要关注基频比重的分布下限。为排除少量异常值，选取1%分位线作为基频比重预警阈值，本文样本数据集得到的基频比重下限预警阈值为0.025；

(5)高低频比: 当变压器发生铁心、绕组机械松动或处于直流偏磁状态时，都会导致频率分布向高频转移，需要关注高低频比的分布上限。为排除少量异常值，选取99%分位线作为高低频比预警阈值，本文样本数据集得到的高低频比上限预警阈值为0.136 6。

4.3 预警阈值有效性实例验证

为了验证上述设定的预警阈值的合理性和有效性，本文对1例样本库以外的500 kV变压器正常状态案例与3.1小节中的2例变压器异常状态声纹案例进行特征计算，并将结果与特征预警阈值进行对比，如图10所示。预警结果如表6所示。

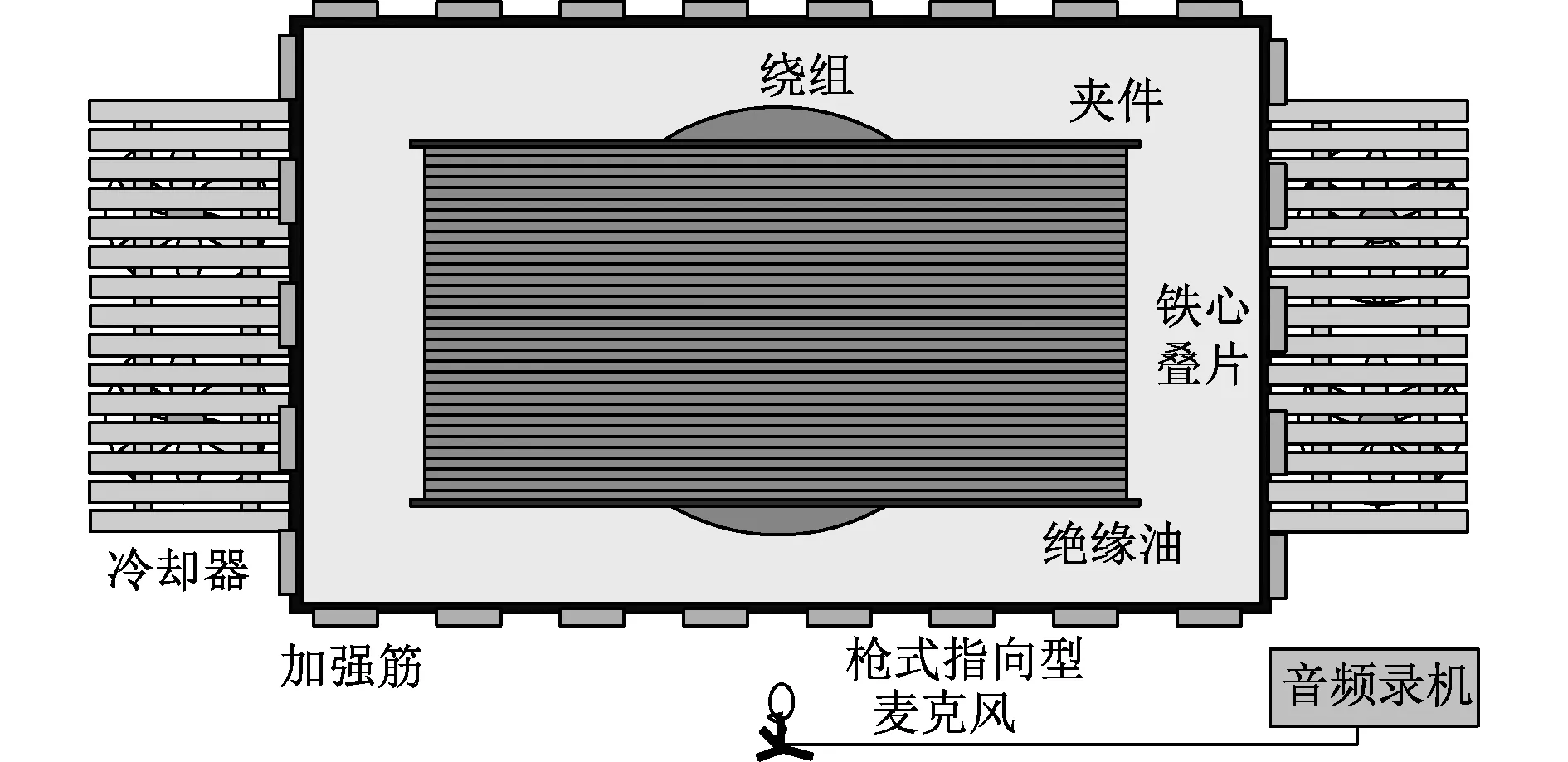
图1 变压器声纹采集方案示意图

表6 现场实测案例样本特征判断

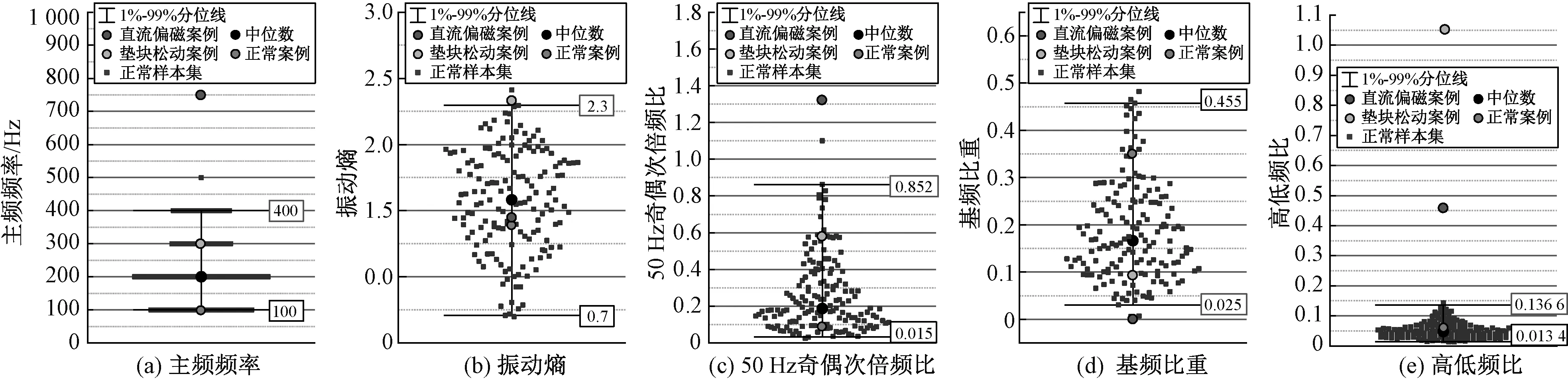
图10 异常案例典型特征值与预警线对比

(1)直流偏磁案例声纹的主频、50 Hz奇偶次倍频比、高低频比4项指标超出预警阈值；

(2)垫块松动案例声纹的振动熵、基频比重、高低频比2项指标超出预警阈值；

(3)正常案例的声纹没有指标超出预警阈值。

由以上案例可以看出，本文根据162台河北省超、特高压变压器统计特性给出的预警阈值能够对现场异常状态的变压器声纹进行有效预警，且对正常状态变压器的声纹没有产生误判。

5 结 论

电力变压器运行声音中包含运行状态信息，通过对大量变压器声音信号的采集与分析，可以为变压器的运行状态评估提供重要参考。本文通过采集162台现场实测样本进行特征值预警阈值划定方法，为5项典型声纹特征划定了参考预警阈值。得到主要结论如下：

(1)采用声纹的幅值相角波动性法能够有效消除了风机噪声，能够对后续的声纹特征分析、状态判别等工作提供支撑；

(2)通过筛选比对，本文选出主频、振动熵、50 Hz奇偶次倍频比、基频比重、高低频比等五项最具代表性的声纹特征值，能够反映变压器的激励变化、机械状态变化；

(3)主频、振动熵、50 Hz奇偶次倍频比、基频比重、高低频比五项声纹特征值都服从正态分布或对数正态分布，具有很强的聚集性，具备阈值预警方式的分布特性基础，随着数据增加，能够对变压器声纹特征分布情况进行更准确地描述；

(4)本文划定的特征阈值能够对2例变压器异常状态声纹案例与1例正常状态声纹案例正确判别，证明了本文所提出的特征阈值划定方法具有一定的合理性和实用价值；

(5)本文证明了由正常样本构建的变压器声纹数据库同样具有重要价值。由于正常样本具有广泛的采集基础，能够在短期内大量积累，从而使本文的预警阈值划定方法快速落地应用。