综合能源系统电价制定策略研究

马立荣，王中瑞，夏雨航，王春波，刘瑞琪

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

0 引 言

综合能源系统(Integrated Energy System，IES)是对可再生能源、化石能源以及电能、热能等二次能源的有效整合利用，实现了多能生产、转化和储存设备之间的协同管理、互补互济。相较于传统供能形式，IES能够以较高的能源利用率和环境效益满足多元化的用能需求，因此是缓解目前日益严峻的能源与环境形势的有效措施，被认为是未来一种重要的能源利用形式[1]。

一般来说，IES系统包含较多的能源模块，如何对各能源模块进行协调调度是需要解决的关键问题。作为IES应用研究的重要基础，IES调度是指在预测次日各时段可再生能源出力和负荷数据的基础上，根据经济性辅以可靠性、环保性等准则，对系统内的可控设备进行统一调度管理以满足各种用能需求[2]。

目前国内外关于IES调度的研究主要致力于IES架构及设备建模[3，4]、降低不确定性因素影响[5，6]、提升环境效益[3,7]、融合需求响应手段等方面。需求响应[8]指用户响应价格信号及激励机制，改变自身固有用电习惯的行为，可分为激励型响应和价格型响应两类。激励型响应是指具有调节能力的大用户在特定时段根据调度部门制定的激励计划改变用电习惯，并从中获得经济补偿的响应行为；而价格型响应(Price-based Demand Response，PDR)是指通过调整电价引导用户自发地错峰用电，包含分时电价(Time-of-use，TOU)、实时电价(Hourly Spot Price，HSP)等形式，具有调整范围广、幅度大、实施时间长的特点。

许多研究者针对PDR策略在IES调度的应用进行了大量研究。在IES响应机制方面，崔杨[9]构建了响应上级电网实时电价的风-光-光热IES日前优化调度模型；Luo Yan-Hong[10]对电动汽车、空调和储能设备在分时电价下的响应机制进行建模分析，提出了考虑经济性和环保性目标的多能源枢纽协同运行模式；Wang Can[11]建立了针对不同负荷类型的调度弹性及补偿机制的需求响应模型，在此基础上建立IES多目标调度优化模型；以上研究皆通过算例验证考虑PDR手段的调度方式可提升系统运行经济性及风光资源消纳能力、降低系统污染排放水平。此外，赵峰[12]进一步将PDR作为微电网调度手段，根据微网负荷率制定实时电价，并据此建立孤岛微网调度模型；为了进一步挖掘需求侧调度潜力，王佳颖[13]构建了考虑风光出力不确定性和PDR微网系统运行优化模型，以电热能源实时零售价格信号引导用户参与响应，提升微网系统整体运行效益。

综上，研究者们对IES调度方面进行了大量的研究工作，取得了丰富的研究成果。然而总结目前研究，存在以下两方面不足：(1)对于PDR手段的应用，通常IES只是适应某种电价模式，不仅对用户利益的考量有限，而且缺乏对其合理性的研究，负荷侧需求响应能力的有限；(2)仅考虑单一电价形式，未进行不同电价方案间的对比分析，不利于IES在实施PDR策略时做出合适的决策。

为解决上述问题，本文首先以用户电负荷波动最小为目的设计了分时电价和实时电价定价模型，并构建了峰谷差、负荷转移率等指标评价不同电价对用户用电行为的影响，通过该模型降低整体用电负荷的峰谷差，提升IES运行的稳定性，降低系统运行成本；随后建立IES日前经济调度模型，在满足不同电价对应负荷需求的前提下，以最小化系统运行成本为目标规划IES运行计划，通过对比各电价方案下IES经济性最佳的系统运行成本，更加完善地讨论不同电价方案对IES经济效益的影响情况。本文为IES实际运行中合理选择电价方案提供一种参考方法。

1 需求响应弹性模型

根据电力系统经济学原理，用户会根据电价变化自发调整用电习惯，即对电价信号做出响应行为，以保证自身利益最大化。为了表征负荷需求量对价格变动的敏感程度，按公式(1)定义需求弹性系数：

(1)

式中：εe(s,t)为s时段对t时段的需求弹性系数；ΔPload(s)为s时段实施PDR后电负荷变化量，kW；Pload(s)为s时段原始电负荷，kW；Δρ(t)为t时段实施PDR后的电价变化幅度，元/kW·h；ρ(t)为t时段原始电价，元/kW·h。

用户负荷需求按是时间上的转移特性分为两类[14]：只可根据价格调整需求量多少、不可进行时间上转移的称为自弹性需求，弹性系数≤0；可依价格从高价时段转至其他时段的称为交叉弹性需求，弹性系数≥0。用户负荷需求自弹性模型如下：

用户负荷需求响应交叉弹性模型为

(3)

根据式(2)和(3)，考虑到用户根据电价水平进行的负荷削减和转移行为，负荷随电价变动的综合需求弹性模型为

(4)

2 电价优化模型

上节分析了用户需求随价格变化关系，在此基础上，本节主要介绍分时电价和实时电价这两种PDR形式的制定方式。分时电价是指电力部门根据电力生产成本的差异划分峰谷时段，并制定不同的电价[15]；实时电价是一种动态的、随成本实时浮动的电价，反映电力市场的实时供需状况[15]。这两种电价可以有效引导用户改变用电习惯，从需求侧进一步提升IES的调控潜力。

2.1 分时电价优化模型

假设已知IES的原始负荷及电价情况，通过分析历史负荷数据，完成建立需求弹性系数矩阵并进行峰谷时段的划分。对于不同时段的电价取值，本文建立以下优化模型。

优化决策变量选为峰平谷时段的电价，为降低用电负荷曲线波动，优化模型的目标函数为

(5)

需满足以下约束条件：

(1)电价约束

分时电价的价格水平关系到供需双方的利益，因此对峰平谷时段电价进行限制，如公式(6)所示。

(6)

式中：ρv、ρf、ρp分别为谷、平、峰时段的电价，元/kW·h；ρv,max和ρv,min分别为谷时电价的上下限；ρf,max和ρf,min分别为平时电价的上下限；ρp,max和ρp,min分别为峰时电价的上下限。

(2)峰谷电价比约束

通过对峰谷时段电价比例进行一定的范围限制，防止峰谷倒置、响应不足等现象的出现，确保达到削峰填谷的目标[16]，如公式(7)所示。

(7)

式中：θmin和θmax分别为峰谷电价比例的最小值和最大值。

(3)用户用电成本约束

为了有效激励用户自发地积极响应分时电价策略，需保证其在分时电价下的用电总成本不高于原有的成本，即

(8)

式中：n为调度周期，这里为24 h。

(4)日负荷总量约束

一般来说，分时电价方案的实施不应引起负荷需求较大幅度的变化，因此有

(9)

式中：r为分时电价后总负荷变化率的允许限度。

(5)边际成本约束

为保证IES的利益，规定谷时电价不低于该时段的边际成本，即

ρv≥Rmc

(10)

式中：Rmc为IES的边际成本，元/kW·h。

2.2 实时电价优化模型

为与调度统一时间尺度，本文在制定实时电价时，以每小时电价水平为优化变量，目标函数与分时电价优化模型一致，如式(5)所示。

需满足的约束条件为

(11)

此外还应满足约束条件(8)～(10)。

同时，为了评价用户负荷的变动程度，进而比较用户对新的电价策略接受程度，按式(12)定义用户负荷转移率μ。

(12)

3 IES经济调度模型

本节介绍IES经济调度模型，首先对系统设备建立数学模型，然后以系统运行总成本最小为目标，以可控设备功率大小为优化变量，构建了IES经济调度模型，用于计算经济性最佳状态下的系统运行总成本，同时也为IES实际运行提供参考计划。

3.1 IES主要供能单元模型

如图1所示，本文以典型的电热联合供应综合能源系统为例，对IES的主要设备进行建模分析，包含风力发电系统(Wind Turbine，WT)、分布式光伏发电系统(Photovoltaic，PV)、分布式燃气热电联供系统(Combined Heat and Power，CHP)、燃气锅炉(Gas Boiler，GB)、电储能系统(Electric Storage System，ESS)、热储能系统(Heat Storage System，HSS)，暂不考虑网路传输引起的能量损失；此外系统与上级电网间处于并网交互运行模式，即IES可作为负荷单元向电网购电，当其内部电能过剩时，又可实现余电上网[17]。

图1 综合能源系统结构示意图

(1)风电、光伏发电系统

目前许多研究如文献[18，19]通过机器学习等方式实现根据风速、辐射强度、气温等环境因素，对风电和光伏发电功率进行较为准确的短期预测。基于此本文假设IES将风电和光伏出力以预测功率最大值运行，最大化利用可再生能源，暂不考虑预测误差及突发气象状况对IES调度影响。

(2)热电联产系统

CHP系统供能部件有燃气轮机(Gas Turbine，GT)和余热锅炉(Waste heat boiler，WHB)，其中燃气轮机输出功率、燃料消耗、发电效率、余热回收功率之间的关系式如下[20]：

PGT(t)=ηGT(t)·VGT(t)·RLHV

(13)

QWHB(t)=PGT(t)·ηWHB·

(14)

(15)

(16)

式中：PGT(t)和QWHB(t)分别为t时段燃气轮机输出电功率和余热锅炉回收烟气余热产生的热功率，kW；ηGT(t)为t时段燃气轮机发电效率；VGT(t)为t时段燃气轮机天然气消耗速率，m3/h；RLHV为天然气的低位热值，取9.7 kW·h/m3；ηWHB为余热锅炉效率；ηGB,loss为燃气轮机散热损失率；a3、a2、a1、a0为燃气轮机效率拟合曲线系数，取值与实际燃气轮机机组有关，本文取值为0.234 3、-0.644 9、0.688、0.082 8；βGT(t)为燃气轮机的负荷率；PGT,r为燃气轮机的额定发电功率，kW。

(3)燃气锅炉

燃气锅炉运行效率、燃料消耗及输出功率关系式如下：

QGB(t)=ηGB·VGB(t)·RLHV

(17)

式中：QGB(t)为t时段燃气锅炉输出热功率，kW；ηGB为燃气锅炉供热效率；VGB(t)为t时段燃气锅炉天然气消耗速率，m3/h。

(4)电储能系统

电储能系统一般由多组蓄电池以及逆变器、能量管理系统等部分构成，可以平抑IES运行中风光出力及负荷波动。其运行过程中实时容量与充放电功率的关系如下：

(18)

(19)

式中:NESS(t)为t时段电储能设备的容量，kW·h；σESS为ESS能量自损率；ηESS,ch和ηESS,di分别为ESS充、放电效率；PESS(t)为t时段ESS充放电功率，kW，其负值代表充电过程，正值代表放电过程；Δt为调度周期；SOCESS(t)为t时段的ESS蓄能状态，%；NESS,r为ESS额定容量，kW·h。

(5)热储能系统

在IES运行过程中，通过控制热储能系统的充能及放能过程，可以实现热能在时间上的平移，有效提升IES运行的灵活性。HSS实际运行状态模型可参照电储能系统模型，即将式(18)和(19)中的角标ESS替换为HSS。

3.2 IES调度优化模型

本文将IES调度优化模型的目标函数设为系统运行总成本，优化模型的决策变量为每个调度周期内各可控单元的功率，计算公式如下：

f=minCtotal=min(Cfuel+Cgrid+COM)

(20)

式中:Ctotal为系统运行总成本，元；Cfuel为燃料购置成本，元；Cgrid为系统与上级电网交互成本，元；COM为设备运行维护成本，元。

燃料购置成本由设备燃气轮机和燃气锅炉的运行产生，因此有

(21)

式中:pNG为天然气单价，元/m3。

系统与电网交互成本模型如下：

(22)

式中：Pgird(t)为t时段与上级电网交互功率，kW，其值为正数时为从上级电网购电，反之为向上级电网售电；pgird(t)为t时段与上级电网购电及售电的价格，元/kW·h。

设备运行维护成本模型如下：

pGBQGB(t)+pESS|PESS(t)|+pHSS|QHSS(t)|)×Δt]

(23)

式中：PPV(t)和PWT(t)分别t时段为光伏和风机系统输出功率，kW；pPV、pWT、pGT、pGB、pESS、pHSS分别为设备PV、WT、GT、GB、ESS、HSS的单位运行维护费用，元/kW·h。

模型涉及的约束条件如下：

(1)电功率平衡约束

PPV(t)+PWT(t)+PGT(t)+

Pgrid(t)+PESS(t)=Pload(t)

(24)

(2)热功率平衡约束

QWHB(t)+QGB(t)+QESS(t)=Qload(t)

(25)

式中：Qload(t)为t时段用户用热负荷，kW。

(3)联络线功率约束

Pgrid,min≤Pgrid(t)≤Pgrid,max

(26)

式中：Pgrid,max和Pgrid,min分别为系统向上级电网购电及售电的功率上下限，kW。

(4)可控设备功率约束

(27)

式中：PGT,max和PGT,min分别为GT功率上下限，kW；QGB,max和QGB,min分别为GB功率上下限，kW；PESS,max和PESS,min分别为ESS功率上下限,kW；QHSS,max和QHSS,min分别为HSS功率上下限，kW。

(5)储能设备运行约束

储能设备在运行中其SOC状态约束如下：

(28)

式中：SOCESS,min和SOCESS,max分别代表ESS容量上下限值；SOCHSS,min和SOCHSS,max分别代表HSS容量上下限。

(6)燃气设备功率爬坡/滑坡约束

-RGT,down≤PGT(t+1)-PGT(t)≤RGT,up

(29)

-RGB,down≤PGB(t+1)-PGB(t)≤RGB,up

(30)

式中：RGT,up、RGT,down分别代表对应GT爬坡/滑坡速率限值；RGB,up、RGB,down分别代表对应GB爬坡/滑坡速率限值。

3.3 求解方式

对于以上优化模型，常用的求解方式有两种：商用求解器软件(如CPLEX等)和以遗传算法、粒子群算法等为代表的智能优化算法编程求解，其中智能算法适用于求解的问题更加广泛，是解决优化问题的重要手段。本文采用文献[21]中的双适应度混沌粒子群算法，其原理在此不加赘述。

4 算例分析

以国内某园区综合能源系统为研究对象，对其冬季某典型日下电价策略制定及调度进行优化研究。表1为园区供能单元的容量及运行参数，表2为储能系统容量及运行参数，图2为该典型日的电、热负荷及可再生能源出力预测曲线，图3为园区IES与上级电网功率交互价格曲线。

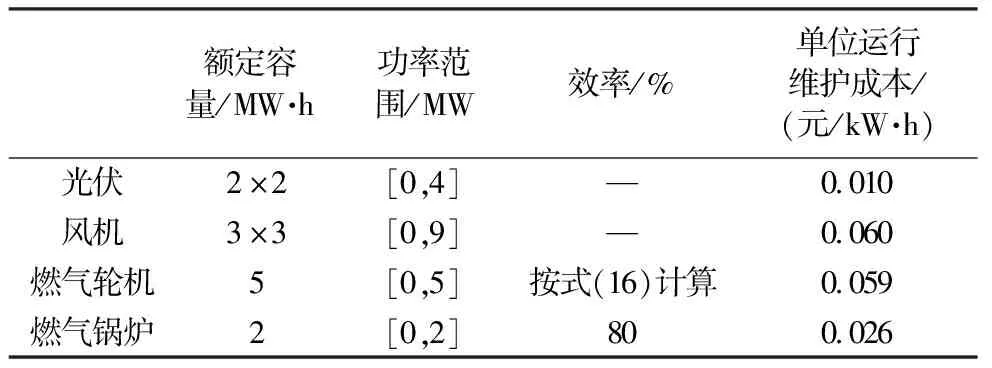
表1 供能设备的容量及运行参数

表2 储能设备的容量及运行参数

图2 园区某典型日的电热负荷及可再生能源出力预测曲线

图3 园区IES与上级电网功率交互价格曲线

4.1 电价优化

园区原始电价为固定电价0.85元/kW·h，分时电价的时段划分及电价范围的选取如表3所示，需求弹性系数参照文献[14]设置，如表4所示。由于分时电价优化问题为线性模型且维度较低，采用标准粒子群算法即可得到良好效果，依据文献[22]具体参数设置为：惯性权重ω=0.729、学习因子c1=c2=1.494，种群规模N=200，迭代步数Miter=300。边际成本Rmc取值0.34元/kW·h[16]，负荷变化率的允许限度r取2%。对于实时电价方案，本文将电价范围设定为[0.3,1.4]，假设需求弹性系数与分时电价相同，该模型下采用文献[21]的改进粒子群算法计算。两种电价优化策略均通过MATLAB软件进行编程计算。

表3 分时电价峰谷时段划分及电价范围

表4 各时段需求弹性系数

图4为不同电价方案及其对应的用户用电负荷曲线，结合表5中的各项电负荷评价指标可以看出，TOU和HSP两种电价方案，由于选取了相同的需求弹性系数矩阵，两种电价对应的负荷曲线在转移趋势上呈现相似性，电负荷都实现了由高峰时段转移向低谷时段的目标；部分时段下的电价明显高于原始的固定电价值，使得用户主动削减了部分非必要负荷，从该典型日内的负荷整体水平来说，TOU和HSP两种电价下，负荷削减量分别占原始负荷的1.98%和1.57%；在可接受范围内。

表5 电负荷评价指标

图4 电价方案及用户用电负荷情况曲线

对于供能系统侧，两种电价优化方案降低了电负荷峰值及峰谷差，减轻了系统运行压力，TOU方案的负荷峰值及峰谷差更低，更有利于IES灵活运行；对用户需求侧，两种电价下用电总成本降低，单位用电成本可基本视作不变，对用户用电行为的影响程度较低，HSP方案下负荷转移率为6.32%，明显低于TOU的7.81%，且用户单位用电成本增长幅度较小，更容易为用户所接受。

4.2 不同电价方案对IES经济性影响

前文已结合实例分析了TOU和HSP两种电价方案对于用户层面的影响，而对于IES的能源生产供应，其经济收益的表现为：用户的用电消费总额降低引起的IES收入缩减；以及推行新的电价机制后降低了用电负荷波动性，从而引起了IES系统运行成本的变化。需综合考量收入和成本两方面的变化来判定TOU、HSP两种电价机制对IES经济收益的整体影响情况。

根据第3节所提IES经济调度模型，在满足固定电价、分时电价和实时电价三种方案对应的负荷需求的情况下，对IES进行以经济性最佳为目标的运行调度优化计算，对比分析不同电价方案对最佳运行条件下系统运行成本的影响。

对比表6中的三种电价方案下IES各项运行成本可知，在TOU和HSP两种方案下，燃料购置费用略微下降，而设备运行维护成本基本不变，这意味着燃气轮机和燃气锅炉设备输出功率总量减小，电热储能设备的总充放能功率增加，对储能设备的控制要求更高；同时电网交互成本减小，意味着IES降低了高峰时段向上级电网购电的费用，提升了低谷时段向上级电网售电的补偿，这是IES运行总成本下降的主要原因。

表6 三种电价方案下IES运行成本

同时，考虑到IES的收入随用户用电总成本降低而降低，TOU和HSP方案下用户各降低了0.22%和0.34%的用电成本，两种电价方案下IES总体经济收益分别提升了0.17和0.09万元，可得出结论：分时电价对IES的经济性收益提升更大，而实时电价更容易被用户接受。

5 结 论

本文对IES电价制定策略及经济调度计划进行建模分析，通过算例对比讨论固定电价、分时电价、实时电价三种方案下的IES运行情况及和用户收益，得出以下结论：

(1)对于供应侧，文中的两种电价方案都引导用户依据价格参与负荷响应行为，实现了对电负荷削峰填谷的目标，并且通过调度优化缓和了电热负荷的错峰性冲突，以最小的系统运行成本完成能源的供应。两种电价方案中，分时电价可为IES带来更多的经济收益。

(2)对于需求侧，两种电价方案对用户用电总成本影响较小；实时电价下用户负荷转移率及单位用电成本增长幅度更低，更易于用户的接受。