基于多故障曲线辨识的负荷模型参数优化策略
盛四清,朱思宇,马赟婷,余 洋
(1.华北电力大学 电气与电子工程学院,河北 保定 071003;2.华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
0 引 言
电力系统动态数字仿真为电力部门规划设计、调度运行、电网特性研究、安全稳定控制分析提供重要的数据和分析支持,而电力系统模型结构及其参数决定了仿真结果的准确性和可信性。由于负荷本身的复杂和时变性,负荷模型需要具有典型性和简便性的同时保证仿真效果,负荷建模仍是相当重要的工作[1,2]。
负荷建模工作主要从模型结构的确定和模型参数的获取两方面进行[3]。常用的负荷模型结构主要包含静态负荷、感应电动机模型的综合负荷模型,并考虑配网阻抗以及分布式电源的影响[4-7]。而获取负荷模型参数方面,常用方法有统计综合法和总体辨识法,统计综合法需统计负荷组成,工作量较大[8],而总体测辨法则将大量负荷等效为一个节点,利用系统辨识理论得到模型参数,无需进行大量统计工作,并且各类电力系统监测平台的发展为总体测辨法的应用提供了大量的数据支持[9],因此总体测辨法近些年来受到广泛关注和应用。
为了提高总体测辨法辨识负荷模型参数的准确性,研究者们进行了大量研究。文献[10-12]对参数辨识算法进行优化改进,以适应负荷模型的非线性,使辨识结果更准确,但以上研究仅考虑了辨识参数仿真曲线与待辨识曲线的拟合效果,并未考虑其他场景的拟合效果。总体测辨法的核心是曲线拟合,当仅辨识某一量测曲线时,辨识参数将会对该量测曲线具有良好的仿真准确性[13],但对其他场景拟合效果未知,而负荷模型应当对多种运行场景尤其是不同故障具有良好的拟合效果。有研究者提出使用多曲线进行负荷模型参数辨识,文献[14]将全部辨识曲线整合为一个故障样本矩阵对负荷模型进行训练,但仅研究了对非机理模型的效果。对机理模型更多的采用分别辨识各曲线,再进行参数综合,即由多曲线得到的多组参数得出一组典型参数。文献[15]采用40%电压波动和60%平均分配的方式确定模型参数;文献[16]采用聚类方法以仿真-实测拟合误差为距离得到典型参数;文献[17]对辨识参数直接求平均的方法进行参数综合,但上述文献均未对待辨识曲线类型进行研究,并且未考虑各参数组的拟合效果。综上所述,待辨识曲线类型的选择和参数综合优化策略还需进一步研究。
因此,本文选择多故障曲线作为待辨识曲线进行参数辨识,首先简要介绍基于总体测辨法的负荷模型参数辨识流程,其次通过分析电力系统故障表现,选取了典型故障-三相永久性短路(简称“三永故障”,以‘TP’代指)、单相永久性短路(简称“单永故障”,以‘SP’代指)、振荡(以‘O’代指)的曲线作为待辨识曲线;再次,引入仿真准确度指标以充分利用不同参数对曲线的拟合效果,采用熵权法确定各指标权重;进而,对三组参数进行参数综合,得到最优辨识参数并与传统单故障辨识参数对比,用其他故障曲线验证最优辨识参数的有效性;最终,采用IEEE-11节点系统验证了所提方法的有效性和推广性。
1 基于总体测辨法的负荷模型参数辨识
1.1 总体测辨法流程
总体测辨法辨识负荷模型参数的流程[1]如下:
(1)确定待辨识曲线,并对数据进行预处理;
(2)选择负荷模型的结构,确定待辨识参数;
(3)选择参数辨识算法并辨识出模型参数;
(4)根据多组曲线重复第(2)~(3)步,得到多组参数,进行参数综合,最终确定一组优化参数。
本节主要确定步骤(2)所采用的负荷模型结构及步骤(3)的参数辨识算法,选择并联分布式光伏模块的综合负荷模型结构(synthesis load model with distributed photovoltaic, SLM-DP)表征系统负荷特性,通过最小化模型输出功率曲线和实际输出曲线的均方根误差(Root Mean Squared Error, RMSE)来辨识模型参数。需要指出的是,本文所提的负荷模型参数优化策略同样适用于其他负荷模型结构。
1.2 SLM-DP模型及待辨识参数
考虑到分布式光伏在配网侧的装机容量日益增大,采用SLM-DP模型来反映分布式光伏含量较高地区的负荷特性,其由综合负荷模型(synthesis load model, SLM)在虚拟母线上并联一光伏发电模块构成,结构如图1所示。
静态负荷部分,我国电网调度及规划部门一般用恒阻抗表示。感应电动机部分采用三阶的机电暂态模型表示,详细公式见文献[5],并由文献[5]可知,待辨识的重要参数有:配电网电抗XD、电动机比例PMP、定子电抗Xs和初始负载率KL,其他参数取典型值:Rs=0,Rr=0.02,Xr=0.12,Tj=2 s,Xm=3.5,A=0.85,B=0.0,XD/RD=15。
分布式光伏模块是由光伏电池模块和控制环节组成,经光伏出线等值阻抗与虚拟母线相连,如附录A1图A1所示。由于光伏发电模块的动态特性主要由逆变器的控制环节影响,考虑到模型结构的复杂性,主要辨识控制环节的参数,光伏电池模块结合工程实际和I-V输出外特性搭建,具体结构及公式见文献[18]。控制系统采用定直流侧电压控制与定功率因数控制的控制模式,如图2所示,其中Vdc-ref为光伏电池阵列模型输出的直流侧电压参考值;Vdc为直流侧母线电压;TMA为有功测量环节时间常数;Vm为交流侧测量电压;KPA、KIA分别为有功比例环节和积分环节放大倍数;Pgen为测量有功值;PFref为参考有功功率值,通过其求得参考功率因数值;TPE为无功测量时间常数。由上述分析得到,分布式光伏模块待辨识参数共6个,分别为光伏出线等值阻抗XPV、直流侧电容值C以及控制系统中的4个控制参数TMA、KPA、KIA、TPE。
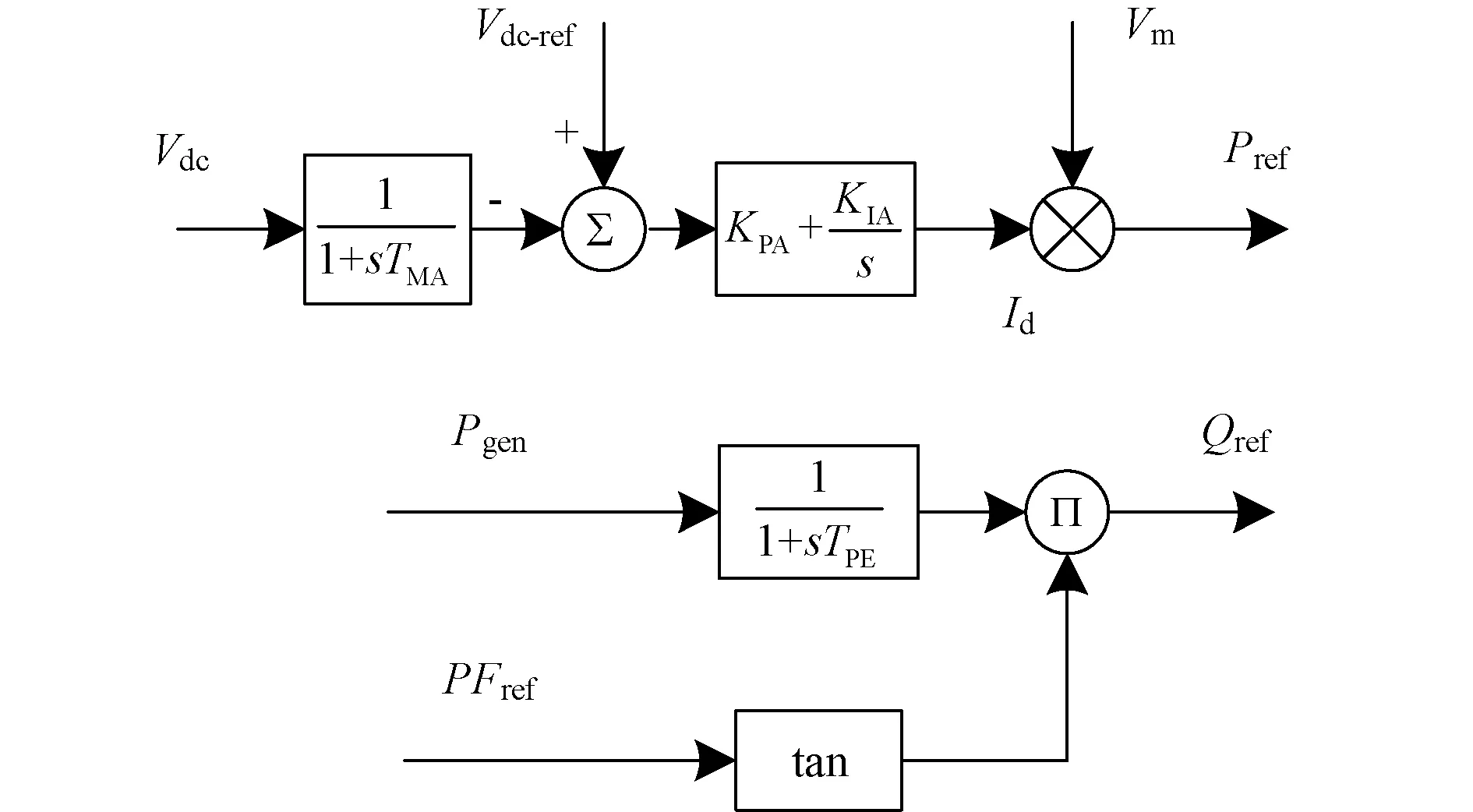
图2 控制系统框图
综上,SLM-DP模型的待辨识参数向量pa为(XD,PMP,Xs、KL,XPV,TMA,KPA,KIA,TPE,C)。
1.3 参数辨识算法及目标函数
均方根误差(RMSE)是衡量模拟值和实测值之间偏差的重要特征值,本文参数辨识采用其作为评估参数辨识结果优劣的判断标准,当采样点数为N时,系统输出有功和无功功率的RMSE如式(1)和式(2)所示,目标函数如式(3)所示。
(1)
(2)
mine=εp+εq
(3)
式中:εp、εq分别为系统输出有功和无功功率的RMSE;Pm、Qm,Pc、Qc分别为有功和无功功率的实测值和拟合值;N为数据样本个数;e为整体误差。
考虑到粒子群算法良好的优化性能和较快的收敛速度,本文采用粒子群算法作为参数辨识算法,详细的步骤参考文献[10]。
2 基于多故障曲线辨识的负荷参数优化策略
2.1 典型故障的选取
电力系统运行时出现的故障类型多样,造成的影响与其类型、位置、持续时间等因素息息相关,将所有故障曲线均用于参数辨识中,数据规模庞大且计算时间过长,而仅采用一种或相似类型的故障曲线难以保证对其他类型故障的仿真效果,因此选取较典型的故障类型作为参数辨识的待辨识曲线。
当发生短路故障时,系统受到冲击,结构发生变化,导致电压潮流等发生大幅度波动,在继电保护装置的有效作用下,故障元件被切断,电压和潮流迅速恢复到稳定状态。其中,三相短路故障是交流系统短路故障中最严重故障,也是电力系统规划设计、安全稳定分析工作中关注度最高的故障类型;另外,单相短路故障作为高压电网中发生概率最大、次数最多的短路故障,有必要对其进行仿真分析。
随着分布式电源的增多,常经由电力电子换流器并网,其作为零转动惯量发电单元接入系统往往会对系统电气阻尼特性造成一定负面影响,而随着负荷的增加和电网互联规模的扩大,系统受扰动后更易出现因阻尼不足导致振荡失去动态稳定的现象。考虑将振荡状态曲线作为待辨识曲线对提高负荷模型动态稳定拟合效果的准确性有重要意义。
综上,选定三永、单永、振荡故障曲线,根据上节的参数辨识流程,辨识出各组负荷模型参数。
2.2 基于仿真准确度指标和熵权法的负荷模型参数优化策略
考虑到负荷建模的目的是为系统仿真建立更准确的模型,因此在进行参数综合时,引入仿真准确度指标作为参数权重的评价指标,采用熵权法 确定各指标权重,从而确定参数权重。
2.2.1 仿真准确度指标的选取及定义
仿真准确度指标的选取既要考虑模型输出与实际输出的整体仿真效果,也应考虑输出曲线中局部重点区域仿真效果,为此,本文采用第1节的整体误差e作为整体仿真准确度指标,另由文献[19]得知,故障切除后的第一摆幅值和后续振荡阻尼特性是输出曲线仿真的重点区域,且后续振荡阻尼特性可采用prony变换法得到振荡频率和阻尼比,因此本文选择有功、无功输出曲线的第一摆幅值、振荡频率、阻尼比的准确度为局部仿真准确度指标。考虑到振荡状态可能并未由大扰动产生,不会出现较大的第一摆幅值,因此其不考虑第一摆幅值指标。具体指标如表1所示。

表1 仿真准确度指标体系
第一摆幅值准确度指标的计算公式为
(4)
式中:AS为第一摆幅值准确度;Sm、Sc为实测曲线、模型拟合曲线的第一摆幅值;g为输出曲线类型判别因子,分为有功P和无功Q。当g=P时,取有功实测、拟合曲线,计算有功准确度指标;当g=Q时,取无功实测、拟合曲线,计算无功准确度指标。
振荡频率准确度指标的计算公式为
(5)
式中:AF为振荡频率准确度;fm、fc为实测曲线、模型拟合曲线的主导振荡模式的振荡频率;g同上。
阻尼比准确度指标的计算公式为
(6)
式中:AD为阻尼比准确度;ζm、ζc为实测曲线、模型拟合曲线的主导振荡模式的阻尼比;g同上。
2.2.2 基于熵权法的负荷模型参数优化策略
熵权法[20]是利用指标信息熵进行权重设定的客观赋权法,熵值越小,信息量越大,其权重也越大。采用熵权法确定指标权重可以得出较客观的评价结果。
负荷模型参数优化策略的具体流程如下:
(1)步骤1:假设有m个待评参数向量pa,形成参数矩阵PA:
(7)
式中:paj为第j个参数向量。
对每个参数向量有n个评价指标,形成原始指标矩阵X=(xjk)m×n:
(8)
式中:xjk为第j个参数向量的第k个指标。
(2)步骤2:数据标准化
由于不同故障对电力系统造成的影响不同,指标数值可能出现几倍的差距,因此将指标数据进行标准化处理,防止出现“大数吃小数”的现象,由于整体误差指标为负向指标,越小越优,则按下式进行标准化得到矩阵Y=(yjk)m×n:
(9)
其他指标均为正向指标,越大越优,则按下式进行标准化:
(10)
(3)步骤3:计算指标比重矩阵P=(pjk)m×n,其公式为
(11)
(4)步骤4:计算第k个指标的信息熵ck,得到信息熵向量c=(c1,c2,…,ck,…,cn),其公式为
(12)
(5)步骤5:计算第k个指标的权重wk,得到指标权重向量w=(w1,w2,…,wk,…,wn),其公式为
(13)
(6)步骤6:计算第j个参数组的权重Wj,得到参数组权重向量W=(W1,W2,…,Wj,…,Wm),其公式为
(14)
(7)步骤7:进行参数综合,得到优化参数向量pabest,其公式为
(15)
3 算例分析
3.1 仿真系统及故障设置
本文在PSD-BPA平台搭建仿真系统,其结构见图3。其中虚线框内为含分布式光伏的简单配网即待辨识负荷区域,箭头表示负荷,DG表示分布式光伏。在C节点得到节点电压、功率响应曲线。
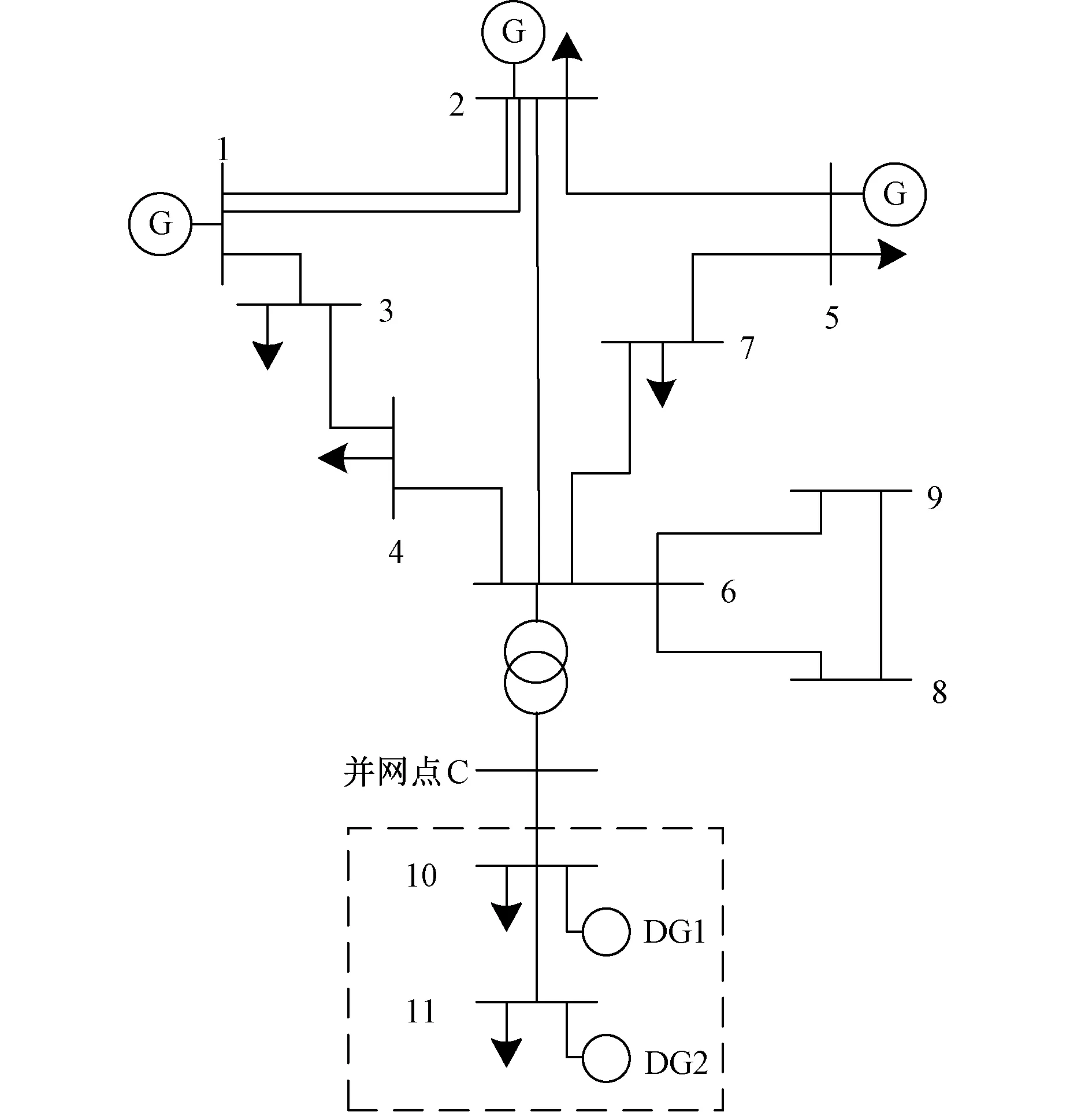
图3 仿真系统结构图
故障发生地点为线路2~6,各故障设置见表2,其中三永、单永、振荡为待辨识故障,两相永久性短路(简称“两永故障”)、单相瞬时性短路(简称“单瞬故障”)为用于测试参数适用性的故障,各故障对应的仿真电压曲线见附录A2图A2。

表2 故障设置表
3.2 辨识结果及参数优化结果
针对三种待辨识故障曲线数据,进行参数辨识得到如表3所示的负荷模型参数。
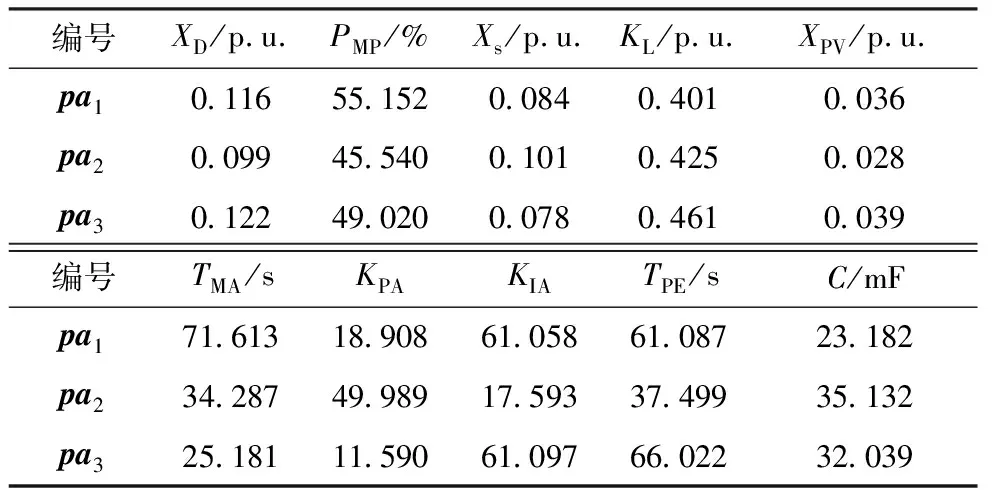
表3 参数辨识结果
由各参数向量对应的负荷模型拟合输出与故障实测输出曲线比较,得到2.2.1节所确定的指标数据如表4所示。
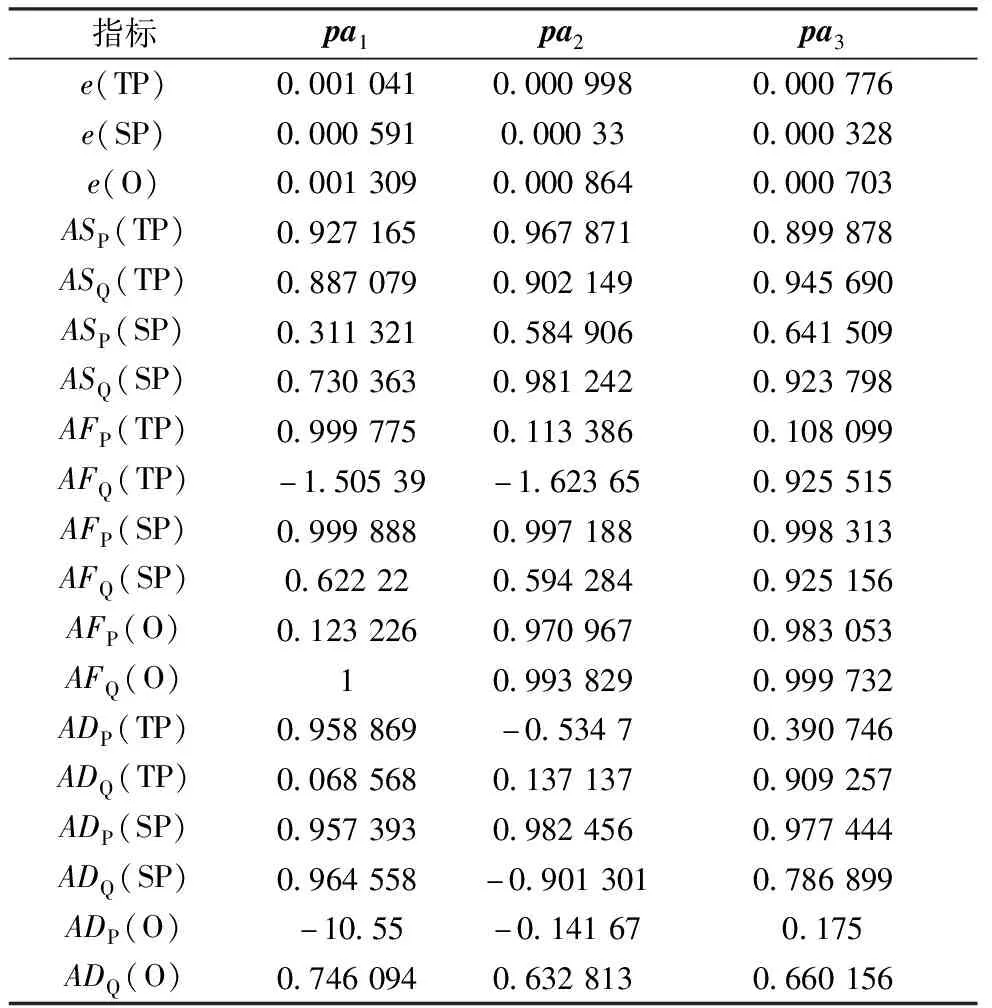
表4 仿真准确度指标
通过式(8)~式(13)得到各指标权重为
w=[0.065,0.038,0.039,0.047,0.056,0.038,0.039,0.099 7,0.086,0.046,0.077,0.038,0.038,0.041,0.078,0.039,0.040,0.038,0.057]。
通过式(14)得到各参数向量的权重系数为
W=[0.143 908,0.430 735,0.781 655]。
最终进行参数综合得到优化参数组如表5所示。

表5 优化参数结果
3.3 优化参数适用性分析
为了验证优化参数的效果和多故障适用性,针对三种典型故障和两种测试故障,对比使用多故障辨识的优化参数组的负荷模型和使用单故障辨识的参数组的负荷模型的输出曲线和故障仿真输出曲线的整体误差,如表6所示。
由表6可见,优化参数组对五种故障均有良好的仿真拟合效果,准确度较高,而采用单故障辨识的其他三组参数对自身辨识故障的拟合效果尚可,但对其他故障的拟合效果一般。因此优化参数组具有更好的多故障场景适用性。
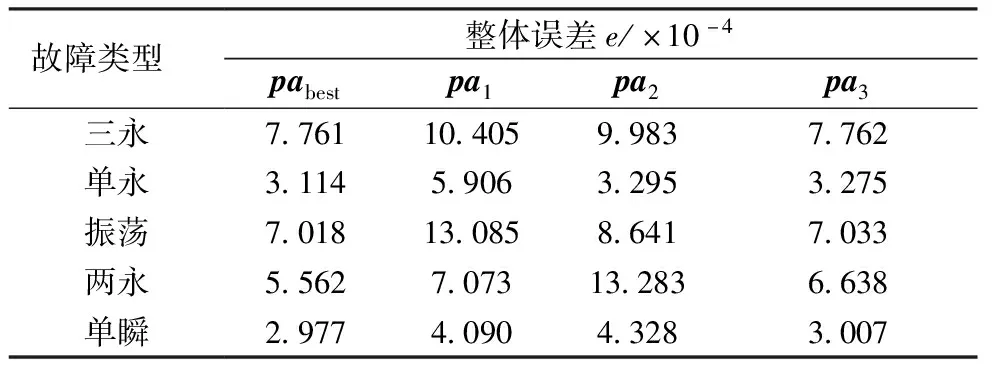
表6 仿真整体误差
单故障辨识的参数组以基于三永故障辨识的参数为例,优化参数组的负荷模型和单故障辨识参数组的负荷模型对测试故障的有功功率、无功功率仿真拟合结果如图4、图5所示。典型故障的仿真结果见附件A3图A3、A4。由图4、图5、图A3、图A4可知,采用多故障法的优化参数仿真结果与故障曲线更为接近,在曲线局部同样表现良好。

图4 有功功率曲线拟合

图5 无功功率曲线拟合
3.4 策略稳定性分析
为了验证所提优化策略的稳定性,进行30余次多故障曲线辨识及参数优化实验,得到拟合整体误差分布图如图6所示,进行基于三永故障的单故障辨识实验30余次,得到拟合整体误差分布图如图7所示。

图6 多故障辨识的参数拟合整体误差分布图
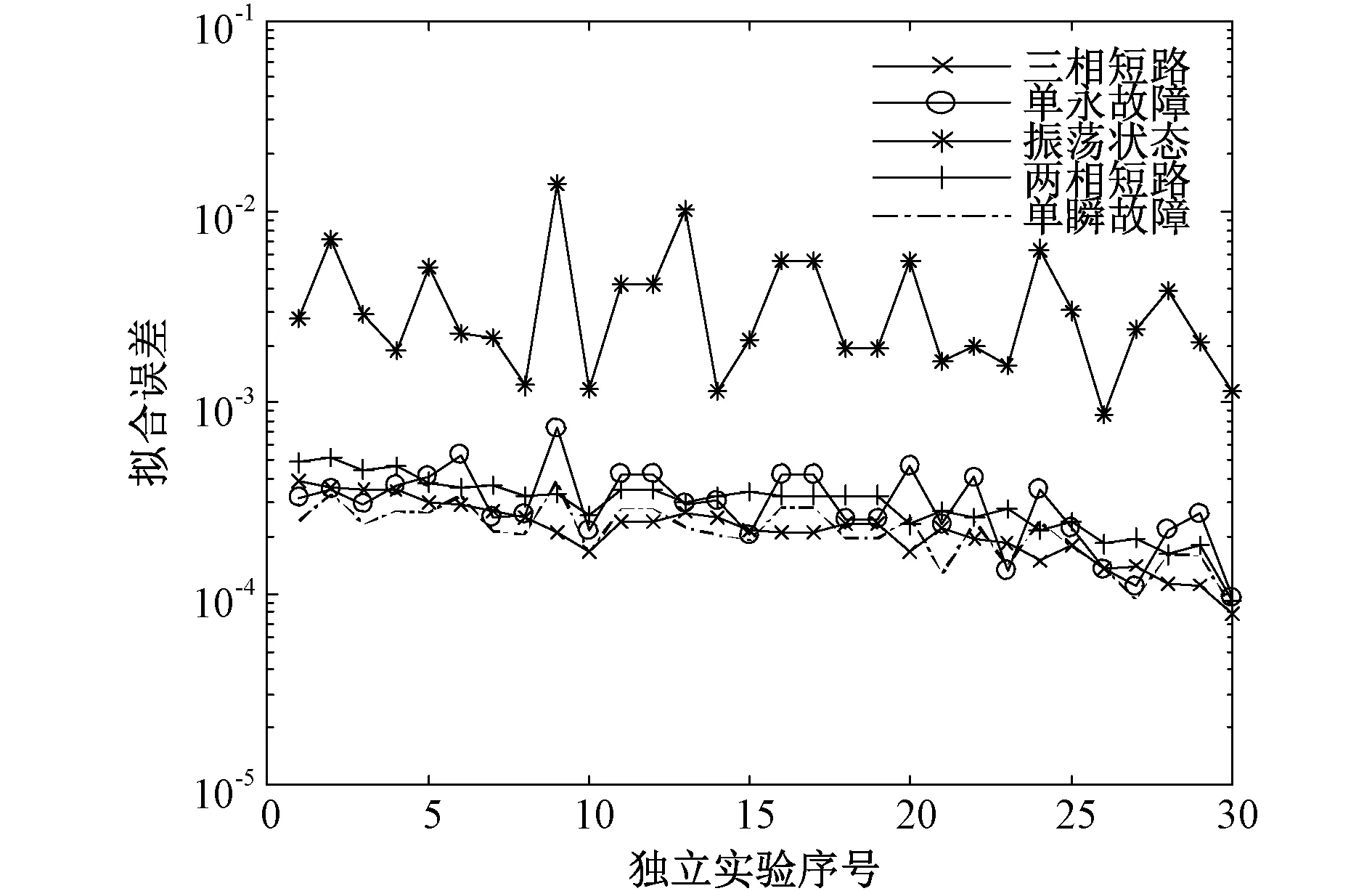
图7 单故障辨识的参数拟合整体误差分布图
对比图6、图7,多故障辨识的优化策略得到的参数拟合误差变化范围在10-4~10-3数量级,单故障辨识的参数拟合误差变化范围在10-2~10-3数量级,说明所提优化策略可以提高参数准确度,且结果相差不大,证明了所提策略的稳定性和有效性。
4 结 论
针对负荷模型仿真准确度提升和多故障场景适用性问题,本文选择三组典型故障进行多故障辨识,基于仿真准确度指标和熵权法进行参数综合和优化,形成基于多故障曲线辨识的负荷模型参数优化策略。策略充分利用仿真准确度信息来确定参数综合时的各组权重,实现了负荷模型参数的优化。最后通过算例验证所提策略的有效性和多故障场景适用性,与传统单故障辨识方法相比,所提策略得到的模型参数仿真效果更好,并且对不同类型故障均具有较好的仿真效果。为提高负荷模型仿真准确度提供了一种新的优化方法。

