具时滞的肿瘤免疫扩散模型的动力学性质分析
刘高杨, 丁宇婷
(东北林业大学 理学院, 黑龙江 哈尔滨 150040)
一直以来,肿瘤都是严重危害人类健康的重大疾病之一.由于环境污染的日益严重和人口老龄化问题,肿瘤的发病率越来越高.尽管人类已经尝试多种办法治疗肿瘤,但是如今肿瘤依然是人类难以攻克的难题.相关研究表明,免疫力低下是形成肿瘤的原因之一.随着分子细胞生物学理论的日益成熟,利用人体的免疫力治疗肿瘤成为医疗工作者的首选方法.
1999年,Sheu等提出了利用免疫逃脱机制治疗肿瘤的观点[1].2000年,Weiner等阐述了放射免疫疗法治疗肿瘤的原理[2].为寻找提高机体免疫力的方法,Coulon等在实验中证明树突状细胞(dendritic cells,DC)能刺激T细胞的增殖,进而增加机体免疫力.通过刺激辅助性T细胞增殖,达到治疗肿瘤的目的,提出利用继承性细胞免疫疗法(adoptive cellular immunotherapy,ACI)刺激免疫系统清除肿瘤细胞[3].2021年,Zhou等指出肿瘤相关巨噬细胞(tumour-associated macrophages,TAM)在治疗肿瘤中起着重要的作用[4].如今,“免疫治疗法”的相关理论正在日益完善.
近些年来,人们利用数学模型这一工具研究提高机体免疫力的方法[5-10],并将Hopf分支理论巧妙地应用其中,取得了丰硕的成果[11-17].免疫细胞能够识别和清除肿瘤细胞,但是由于免疫细胞识别肿瘤细胞具有一定的时间延迟,因此,研究免疫细胞识别肿瘤细胞的时滞对于分析肿瘤细胞与免疫细胞之间的动力学行为是非常重要的.时滞变化能够改变系统平衡点的稳定性,随着时滞的变化,系统可以展现不同的动力学行为.因此,探索时滞引起机体免疫力变化的规律成为治疗肿瘤的关键之一[18-20].
近年来,很多学者构建了各类的时滞微分方程,Kaddar等提出了如下模型用以解释肿瘤细胞的周期解问题[21]:
式中:E是效应T细胞的数量;T是肿瘤细胞的数量;σ是效应T细胞分泌的抗体进入患病部位的速率;ω是效应T细胞的应答速率;δ是效应T细胞的死亡速率;α是肿瘤细胞的最大成长速率;β是环境最大容纳量;τ是免疫系统产生治疗肿瘤的化学物质所需的时间;除了ω之外,其他系数都是正的.
在实际问题中,由于细胞表面糖蛋白等物质的减少,导致肿瘤细胞会发生扩散,因此,在系统中引入扩散项是必要的.另外,考虑到免疫细胞识别肿瘤细胞存在时间延迟,在模型中引入免疫细胞识别肿瘤细胞的时间延迟τ能够更准确地刻画系统的动力学行为.由于肿瘤细胞和免疫细胞只会分布在研究机体范围内,为此,研究如下具有纽曼边界条件的肿瘤免疫扩散系统:
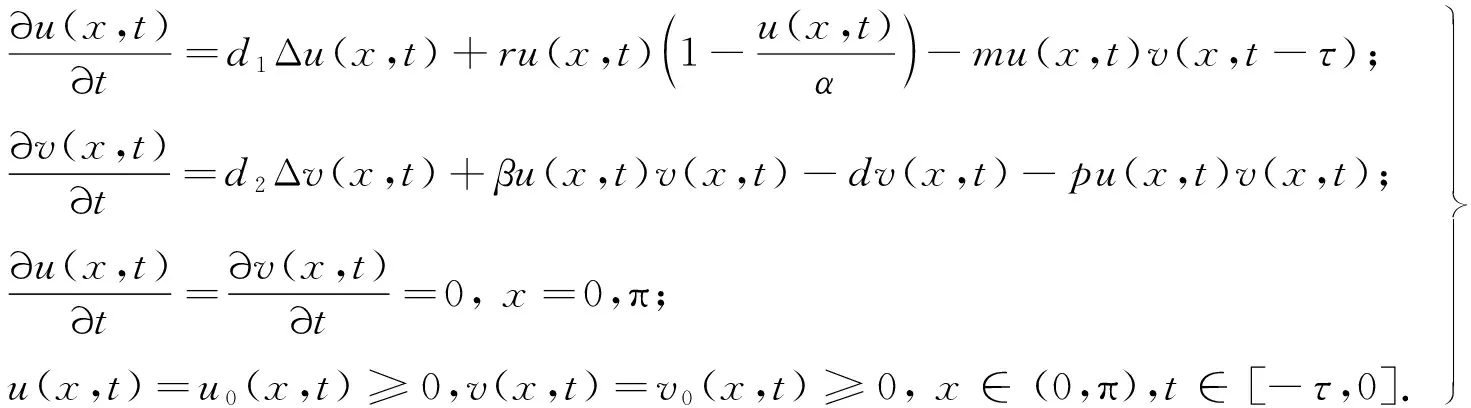
(1)
式中:u和v分别代表肿瘤细胞和免疫细胞的数量;d1是肿瘤细胞的扩散速率;d2是免疫细胞的扩散速率;r是肿瘤细胞自身的成长速率;α是肿瘤细胞的最大环境容纳量;m是被免疫细胞杀死的肿瘤细胞的死亡速率;β是免疫细胞的增长速率;d表示免疫细胞的死亡速率;p表示被肿瘤细胞杀死的免疫细胞的死亡速率;τ是免疫细胞识别肿瘤细胞所需的时间;所有的系数都是正的.
1 系统平衡点的稳定性和Hopf分支的存在性
系统(1)的平衡点满足如下方程:
可得系统(1)的边界平衡点为E0=(0,0),E1=(α,0).假设
(H1):d<α(β-p).
当系统参数满足假设(H1)时,系统存在非平凡平衡点E2=(u*,v*),其中,
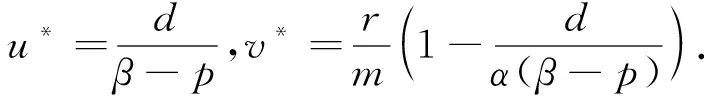
(2)
接下来分析系统(1)的平衡点的稳定性.
在假设(H1)下,令U(x,t)=(u(x,t),v(x,t))T,系统(1)在平衡点(u0,v0)(这里(u0,v0)=(0,0),(α,0)或(u*,v*))处可写成如下形式:
式中:
因此,系统(1)在平衡点(u0,v0)处的特征方程为
λ2+Anλ+Bn+C1e-λτ=0,n∈,
(3)
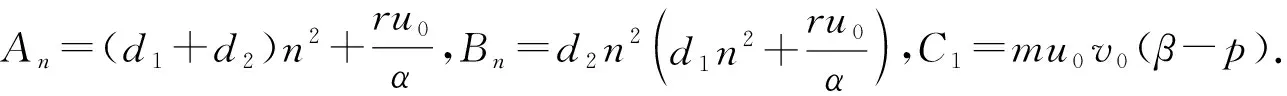
定理1 对于任意τ≥0,系统(1)在平衡点E0处经历B -T分支.
证明 根据方程(3)可得,在平衡点E0(即u0=v0=0)处的特征方程为
λ2+(d1+d2)n2λ+d1d2n4=0,n∈.
(4)
令λ1和λ2是方程(4)的根,则λ1+λ2=-(d1+d2)n2,λ1λ2=d1d2n4.
当n=0时,λ1=λ2=0,因此,系统(1)在平衡点E0处经历B -T分支.
定理2 对于任意τ≥0,系统(1)在平衡点E1处经历不动点分支.
证明 根据方程(3)可得,在平衡点E1(即u0=α,v0=0)处的特征方程为
λ2+(d1n2+d2n2+r)λ+d2n2(d1n2+r)=0,n∈.
(5)
因此,
λ1+λ2=-(d1n2+d2n2+r),λ1λ2=d2n2(d1n2+r).
当n=0时,λ1+λ2<0,λ1λ2=0,所以,当n=0时,特征方程(5)有一个单零根,因此,系统(1)在平衡点E1处经历不动点分支.
下面分析系统(1)在平衡点E2处的稳定性.
定理3 当τ=0时,在假设(H1)下,平衡点E2=(u*,v*)是局部渐近稳定的.
证明 根据方程(3)可得,当τ≠0时,系统(1)在平衡点E2=(u*,v*)(即u0=u*,v0=v*)处的特征方程为
λ2+Anλ+Bn+C2e-λτ=0,n∈,
(6)
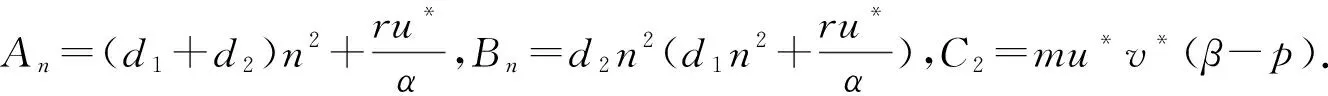
当τ=0时,系统(1)在平衡点E2=(u*,v*)处的特征方程为

(7)
令λ1和λ2是方程(7)的根,于是,
因此,λ1和λ2具有严格的负实部.所以,当τ=0时,平衡点E2是局部渐近稳定的.
为了方便说明,引入如下记号:
当τ≠0时,设λ=iω(ω>0)是系统(1)在平衡点E2处特征方程(6)的根,分离实部和虚部,得

(8)
两边平方相加,得
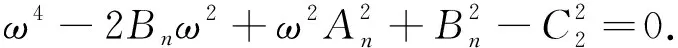
(9)
由式(8)可得

(10)
令z=ω2,可得

(11)

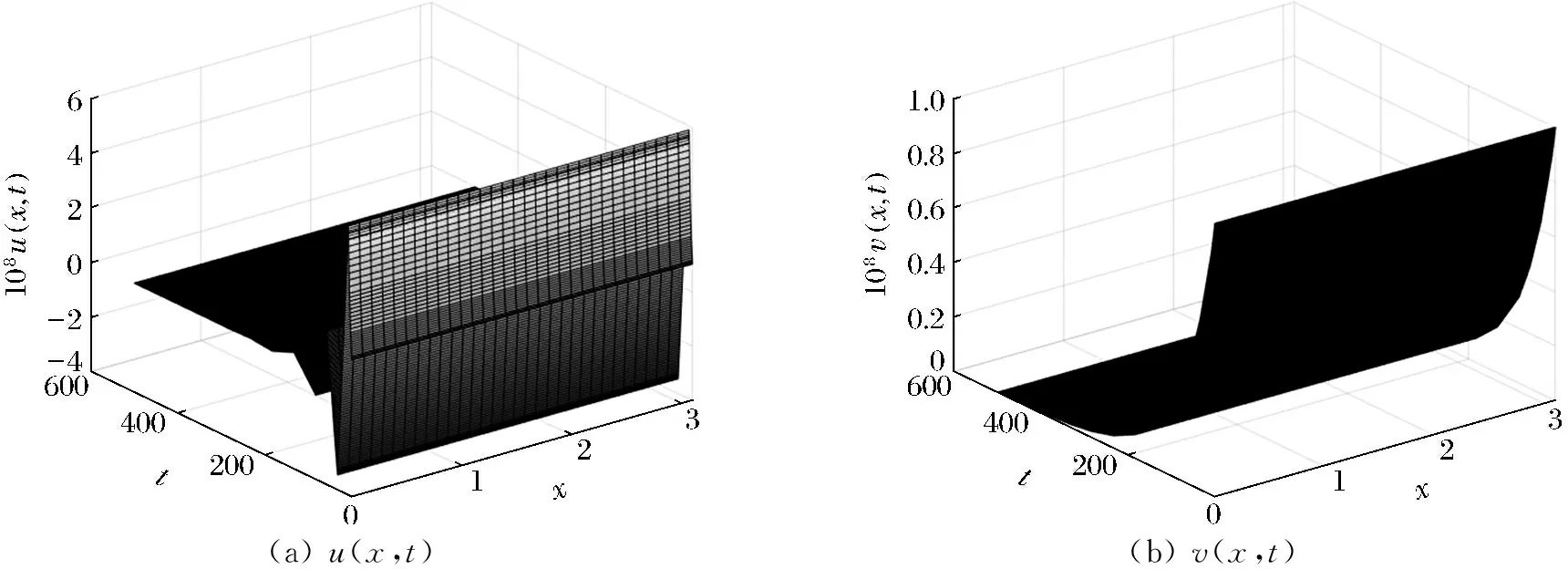
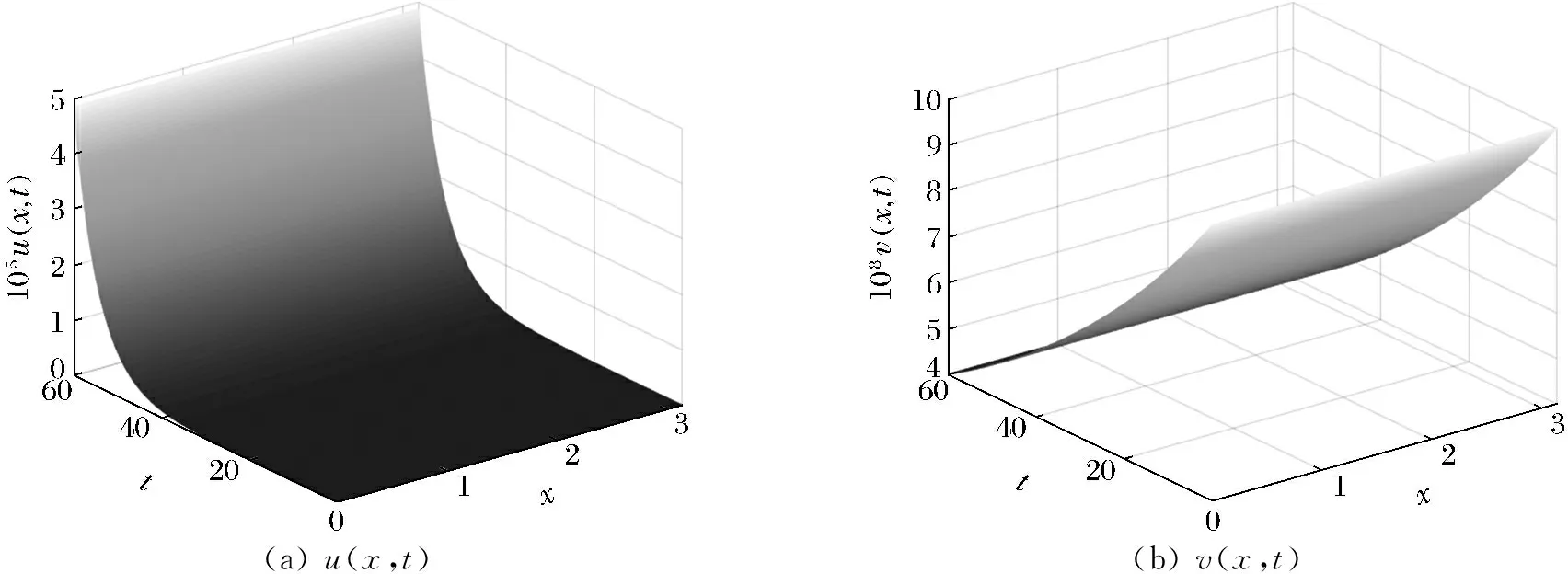
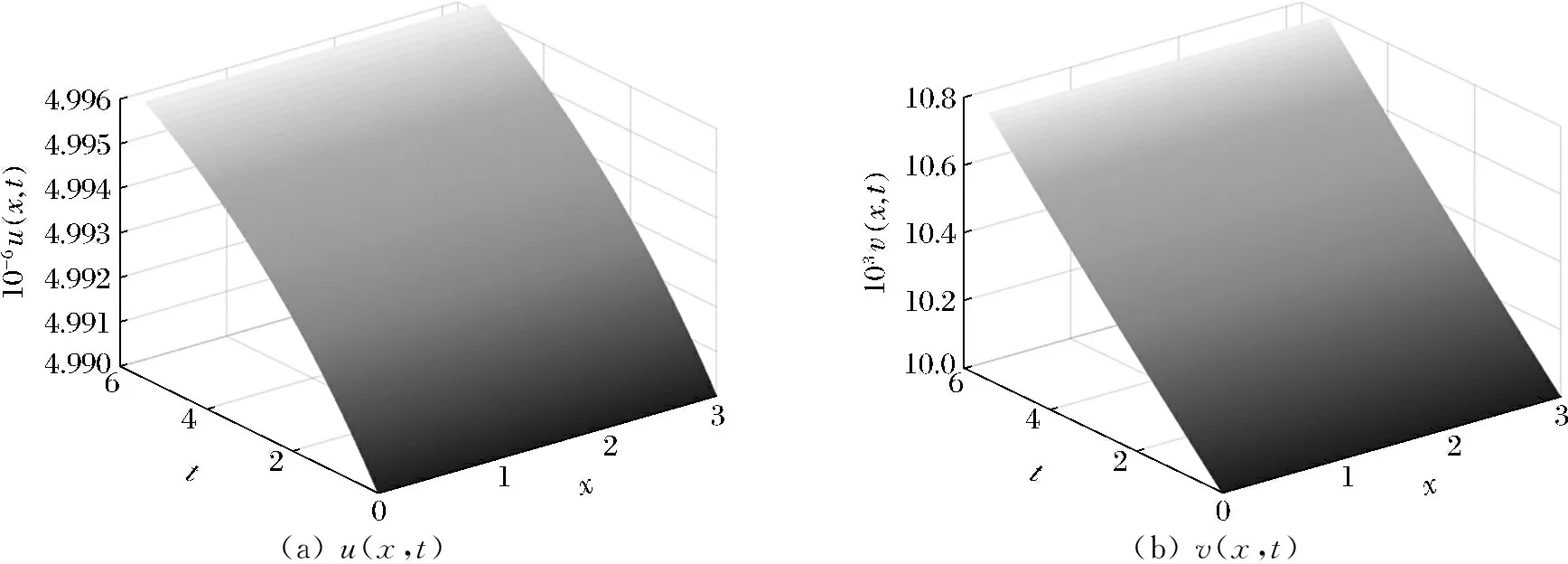
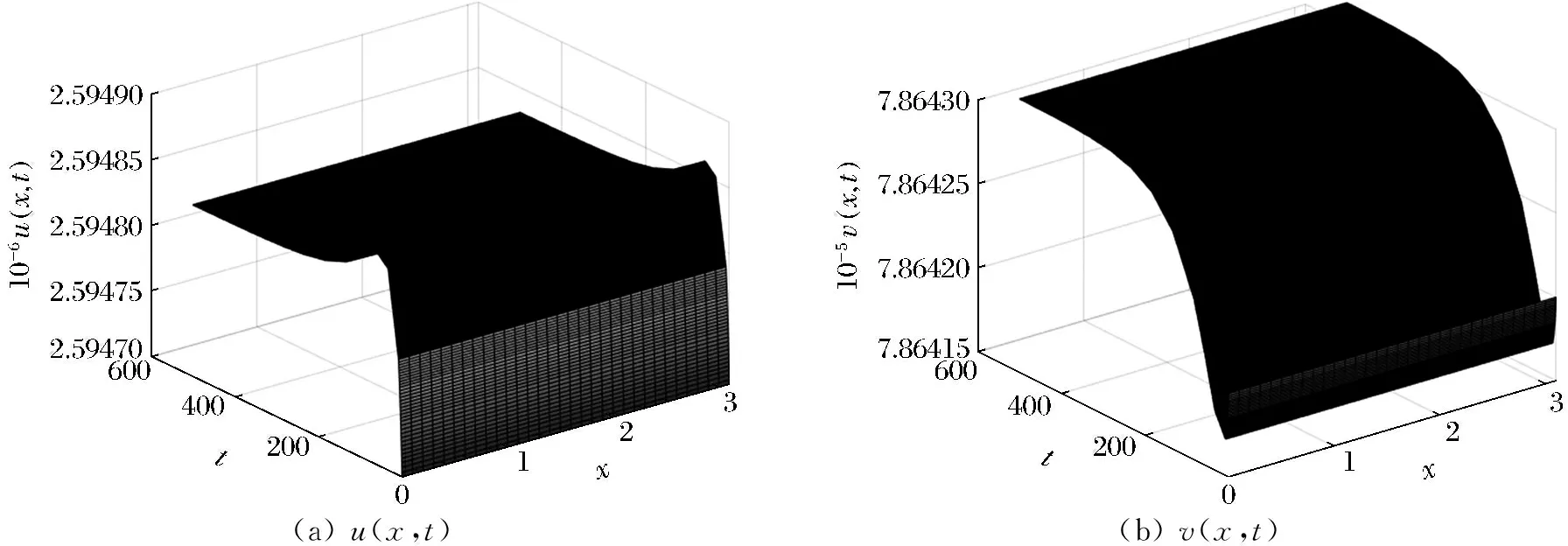
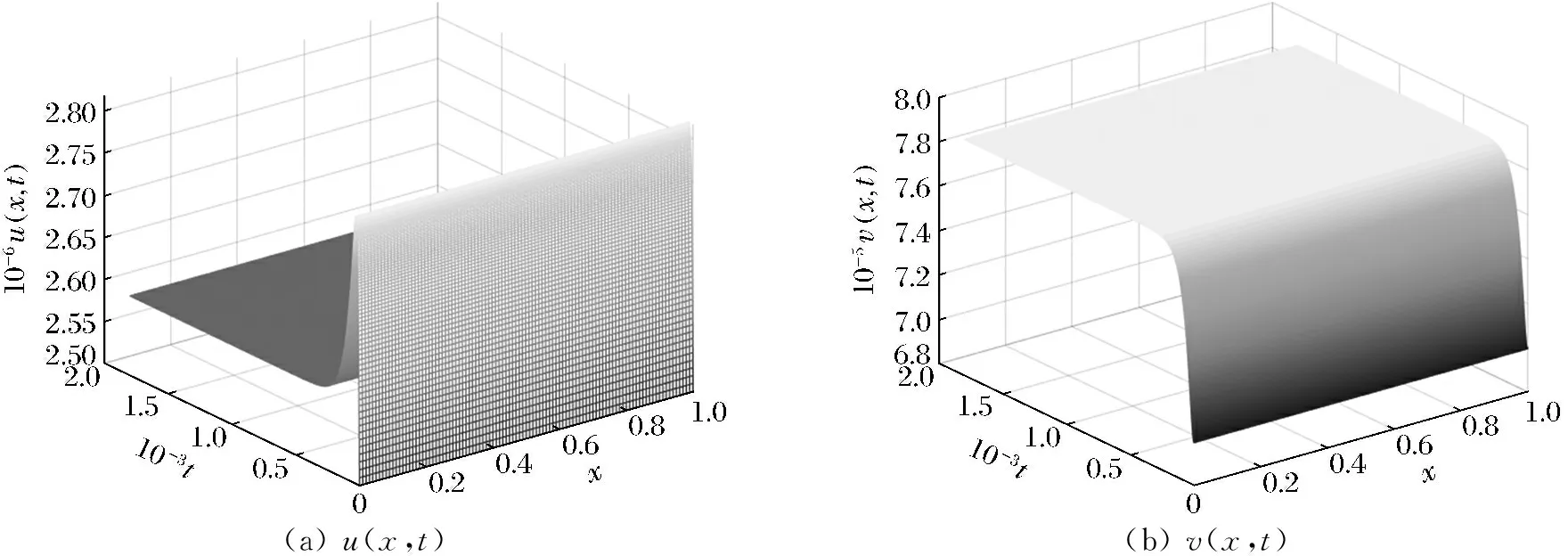
当0≤n (12) 由方程(10)可得 (13) (14) 因此,当τ=τ*时,系统(1)在平衡点E2处经历Hopf分支.结合上面分析,可得定理4. 在本节,利用多尺度方法推导系统(1)在平衡点E2=(u*,v*)处的Hopf分支的规范型. (15) 下面用多尺度方法推导系统(15)的Hopf分支规范型.将式(15)的解设为如下形式: (17) 式中, 此时,对t的导数可化为 令 式中,j∈. 由式(17)可以得 (18) 将时滞部分进行泰勒展开,可得: (19) 式中,uj,1=uj(T0-1,T1,T2,…),vj,1=vj(T0-1,T1,T2,…),j∈. 将式(17)~式(19)代入到式(15),对应ε前的系数,可得: (20) 因此,式(20)的解为 (21) 式中,c.c.代表前面项的复共轭. 对应ε2前的系数,可得如下等式: (22) (23) (24) 式中, 假设 (25) (26) (27) 对应ε3前的系数,可得到如下表达式: (28) (29) 式中, (30) 式中, 因此,系统(15)(或系统(1))截断到三阶的Hopf分支规范型为 (31) 式中,M和χ分别由式(24)和式(30)给出. 1) 当Re(M)μ<0时,约化在中心流形上的分支周期解不稳定; 2) 当Re(M)μ>0时,约化在中心流形上的分支周期解稳定. 根据文献[22]所述,取如下参数:r=0.18 d,α=5.0×106个活细胞,d2=0.2 d,d=0.015 2 d,p=3.422×10-10个活细胞/d,d1=0.02 d,m=1.101×10-7个活细胞/d,β=6.2×10-9个活细胞/d.由式(2)可得,系统平衡点E2=(2.594 8×106,7.864 3×105),由式(12)得 由定理1可知,任意τ≥0,系统(1)在平衡点E0处经历B -T分支.以(0.000 000 001,0.000 000 1)为初值,取τ=0,平衡点E0是局部渐近稳定的,如图1所示;取τ=0.1,平衡点E0是不稳定的,如图2所示.这说明在B-T分支附近,当参数在不同区域时,系统(1)可产生不同的动力学现象. (a) u(x,t)(b) v(x,t) 由定理2可知,任意τ≥0,系统(1)在平衡点E1处经历不动点分支.以(4.99×106,0.01)为初值,取τ=0,平衡点E1是不稳定的,如图3所示;取τ=0.009,平衡点E1是不稳定的,如图4所示.比较图3和图4,虽然平衡点E1都是不稳定的,但是第一个分量从稳定变成不稳定,说明肿瘤细胞发生了扩散,证明了即使免疫细胞识别肿瘤细胞的时滞发生微小的变化,却能影响肿瘤细胞能否发生扩散. (a) u(x,t)(b) v(x,t)图2 当τ=0.1时,系统(1)的平衡点E0是不稳定的Fig.2 The equilibrium E0 of system(1) is unstable when τ=0.1 (a) u(x,t)(b) v(x,t)图3 当τ=0时,系统(1)的平衡点E1是不稳定的Fig.3 The equilibrium E1 of system(1) is unstable when τ=0 (a) u(x,t)(b) v(x,t)图4 当τ=0.009时,系统(1)的平衡点E1是不稳定的Fig.4 The equilibrium E1 of system(1) is unstable when τ=0.009 由定理3和定理4可知,当τ∈[0,τ*)时,平衡点E2是局部渐近稳定的;当τ>τ*时,平衡点E2是不稳定的. 当τ=0时,以(2.5 947×106,7.8 642×105)为初值,平衡点E2是局部渐近稳定的,如图5所示. (a) u(x,t)(b) v(x,t)图5 当τ=0时,系统(1)的平衡点E2是局部渐近稳定的Fig.5 The equilibrium E2 of system(1) is locally asymptotically stable when τ=0 当τ=3<τ*时,以(2.594 7×106,7.864 2×105)为初值,平衡点E2是局部渐近稳定的,如图6所示. (a) u(x,t)(b) v(x,t)图6 当τ=3<τ*时,系统(1)的平衡点E2是局部渐近稳定的Fig.6 The equilibrium E2 of system (1) is locally asymptotically stable when τ=3<τ* 取上述参数,当τc=τ*=92.331 2时,由式(24)和式(30),经过MATLAB计算可得,Re(M)<0,Re(χ)>0,根据定理5,可得系统(15)(或系统(1))在μ>0时具有不稳定的周期解,并且Hopf分支方向是向前的(μ>0). 从生物学的意义上讲,当免疫细胞识别肿瘤细胞需要时间较长时,免疫系统的免疫能力极低,导致肿瘤细胞生长活跃,容易癌变,有向身体其他部位扩散和转移的危险. 本文基于KADDAR和ALAOUI的模型,在模型中引入免疫细胞识别肿瘤细胞的时间延迟τ和扩散项,改进得到了一个偏泛函微分方程(partial function differential equation,PFDE),讨论了该系统的动力学性质.由于肿瘤细胞会发生扩散和免疫细胞识别肿瘤细胞存在时间延迟这两个现象都是影响肿瘤免疫系统动力学性质的重要因素,因此,相对于常微分方程(ordinary differential equation,ODE)和泛函微分方程(function differential equation,FDE),研究结果对于肿瘤的控制和治疗更具有指导意义.研究了时滞对于肿瘤免疫扩散系统平衡点的稳定性以及Hopf分支周期解稳定性的影响.选择时滞作为分支参数,建立了系统非负平衡点稳定的条件.时滞可以影响平衡点的稳定性,当时滞在一定范围内,系统非平凡平衡点是局部渐近稳定的,一旦时滞穿过临界值,系统平衡点失去了稳定性,并且系统产生了不稳定的周期解.当时滞取临界值时,系统经历了Hopf分支.这意味着,当免疫细胞能较快的识别肿瘤细胞时,人体具有较强的免疫力,能抑制肿瘤细胞的增长和扩散;反之,肿瘤细胞迅速增殖,大量聚积在人体,对人体健康产生很大的危害.系统临界值τ*的发现,有助于生物学家对肿瘤细胞的成长进行预测、判断和控制,进而采取有效的治疗手段,最大限度的发挥细胞免疫疗法在治疗肿瘤中的作用.该研究只考虑了免疫细胞识别肿瘤细胞的时间延迟对治疗肿瘤的影响,在以后的工作中,将致力于研究其它因素对控制肿瘤细胞扩散的影响,找到抑制肿瘤细胞恶性生长的条件.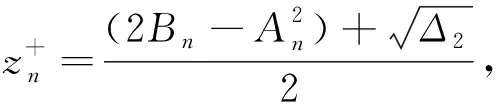


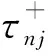

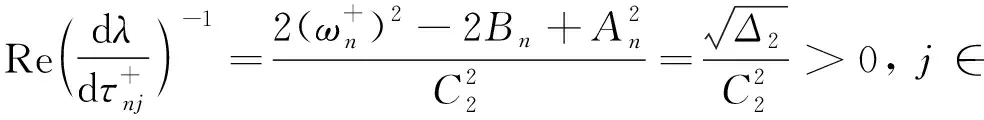
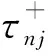
2 Hopf分支的规范型及分支周期解的稳定性
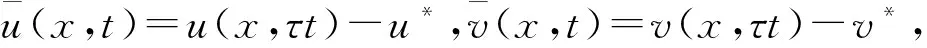
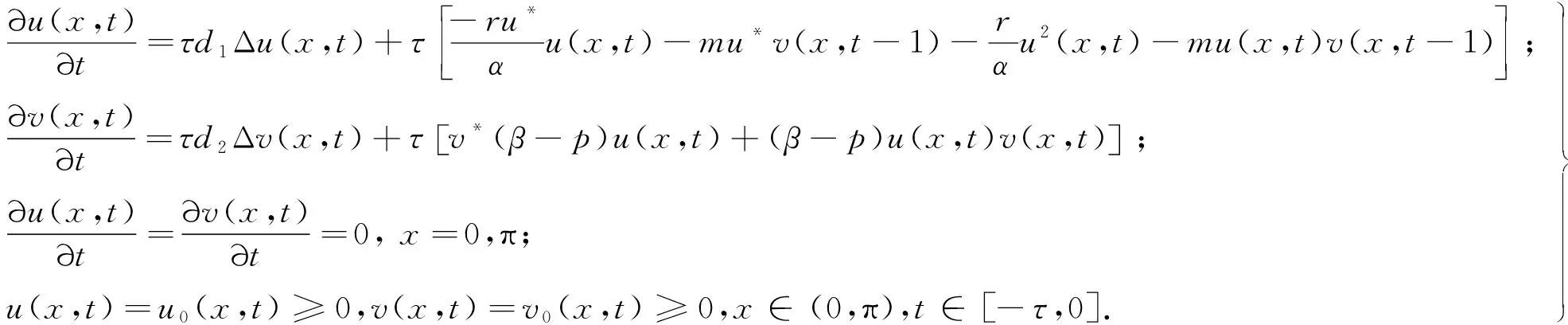
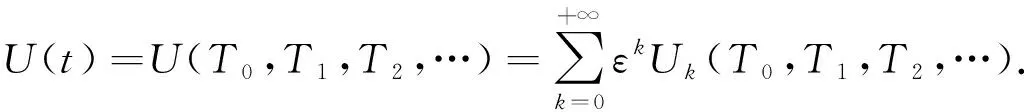
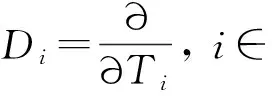
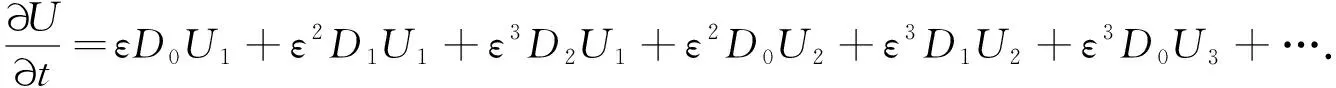
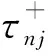
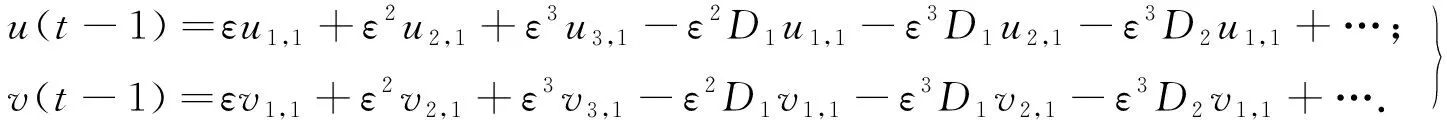
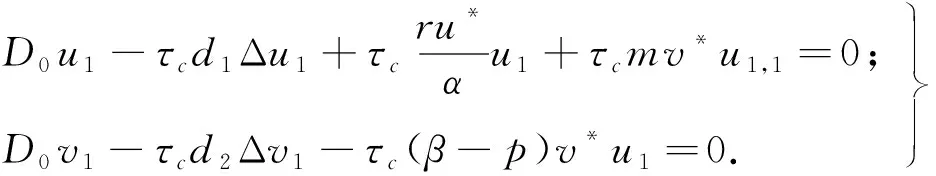
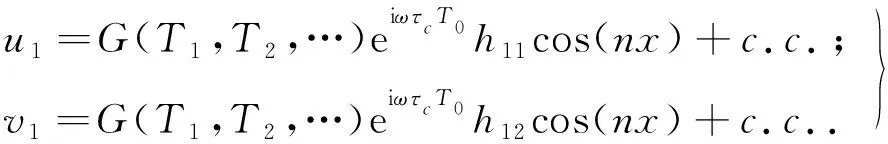

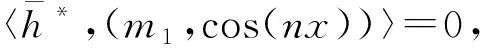

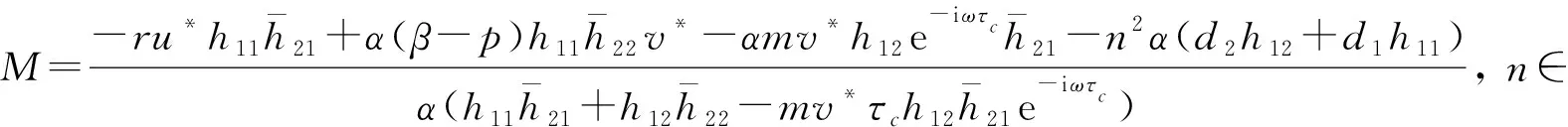
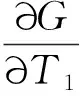

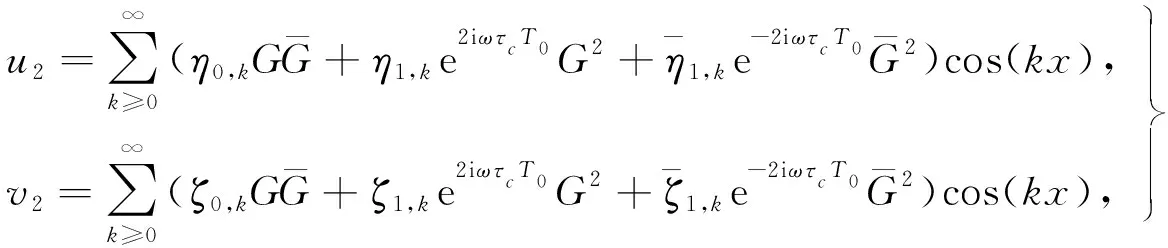

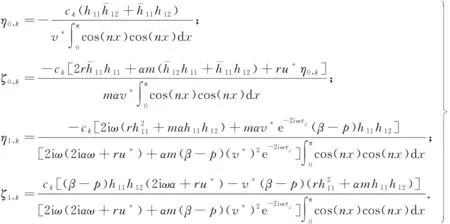

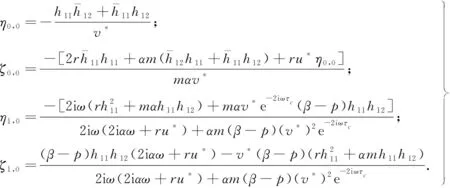
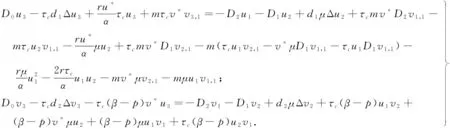
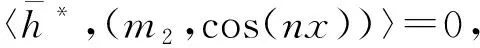

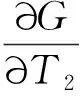

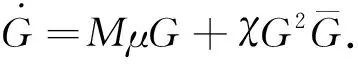
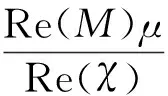
3 数值模拟

4 结 语

