具有精确输入模糊输出的模糊半参部分线性模型
刘晓旭, 曲智林
(东北林业大学 理学院, 黑龙江 哈尔滨 150040)
自从Zadeh[1]发表关于模糊集的开创性论文之后,模糊数学的理论和应用均得到了广泛而深入的研究.模糊回归分析由Tanaka等[2]引入,其认为模糊数据是一种可能性分布,观测值与估计值之间的偏差由于系统结构的模糊性所致.之后D’urso等[3]、Jiang等[4]和Güler[5]以模糊集理论为基础研究了不同的模糊回归模型.Li等[6]和Chen等[7]给出模糊线性模型参数估计的2种方法:线性规划法及最小二乘法.这些模糊回归模型往往用于处理语言变量这类的模糊数.
模糊非参平滑技术近年来也取得了显著的发展,平滑技术对于处理非参数回归问题特别有效.Petit-Renaud等[8]运用模糊数的信念函数进行非参回归分析;Cheng等[9]和Choi等[10]将k近邻和平滑方法扩展到模糊非参回归,然而在统计中这2种方法严重受到边界效应的影响.
半参部分线性模型是参数模型和非参数模型之间的一种折中.Hesamian[11]将半参部分线性模型扩展到模糊环境中,利用有约束的线性规划对模糊系数进行估计,但却没有给出模糊系数估计的显式表达式;并采用k近邻的方法对模糊光滑函数进行估计,但是众所周知k近邻严重受到边界效应的影响.所以本文基于此对上述模糊半参部分线性模型进行改进,提出了含有精确输入、模糊输出、模糊系数、模糊光滑函数的模糊半参部分线性模型.
1 基本理论

式中L,R:+→[0,1]都是左连续非增函数,则称为LR型模糊数.L(x)和R(x)分别称为左右形状函数,a∈叫作的中心值,la,ra∈+分别叫做的左、右扩散,记LR模糊数为

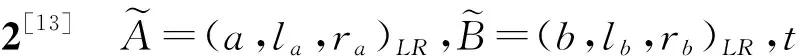

定义4 如果一个矩阵中的元素都是LR模糊数的形式,称这个矩阵为LR模糊矩阵.
定义5 2个LR模糊矩阵和一个实数矩阵t:

1) 模糊矩阵加减定义为
2) 实数矩阵乘模糊矩阵定义为


式中ωm,ωl,ωr>0为权重.
为了确定模型的权重,常常采用以下2种核函数:
1) Gauss[16]核
2) Epanechnikov[16]核
2 模糊半参部分线性模型及其估计方法
2.1 模糊半参部分线性模型
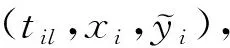
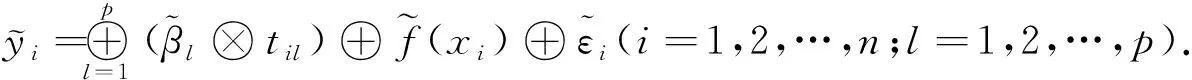
(1)
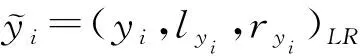
2.2 模糊光滑函数的估计
估计出的模糊输出的隶属函数应该尽可能接近相应观察到的模糊数的隶属函数.从这点出发,采用模糊数之间的距离测度来间接地表示模糊输出的估计值与实际观测值的差异.

(2)
式(2)等价于


(3)
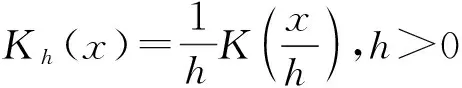
为了方便推导将其转化成为矩阵的形式,

(4)
式中:
式(4)L()对未知参数求导,令其为0,得到在x0邻域内的估计值为
则3组待估参数(c(x0),c′(x0)),(l(x0),l′(x0)),(r(x0),r′(x0))的估计值可以表示为
令
H(x0;h)=(XT(x0)W(x0;h)X(x0))-1XT(x0)W(x0;h).
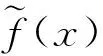

2.3 模糊系数的估计

(6)
为了推导方便,将式(6)转化成矩阵形式
式中:
则有
式中D=eTH(X;h).

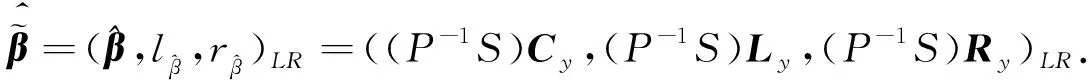
(7)
式中:P=tTDt+tTDTt-tTt-tTDTDt;S=tTDT+tTD-tTDTD-tT.
同理,令x0分别为设计点x1,x2,…,xn,就可以得到各点处模糊光滑函数估计值.
3 带宽的选取
在经典的统计问题中,常用来确认带宽h的方法有广义交叉验证GCV[17],风险估计[18],Bootstrap[19]等,在本文中采用模糊环境下的留一交叉验证方法.

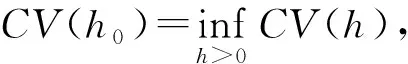
4 拟合度的评判标准
模糊回归问题中模糊非参项拟合程度的度量采用GOF和BIAS 2种方法[20]:
二者的值越小,代表模糊非参项的拟合效果越好.RBIAS相对于RGOF的取值要更加精确,因为它只涉及到了模糊非参项,但是此方法只适用于模拟的情况下.
为了评价本文模型整体的拟合情况,给出几种评测模型拟合度的指标[20].
1) 均方误差(MSEe):
2) 平均百分比误差(MPEe):
3) 平均绝对百分比误差(MAPEe):
4) 对称平均绝对百分比误差(SMAPEe):
这4种拟合度的指标都是关于模型整体拟合程度的一种测量,通过计算模糊响应变量的估计值与其观测值之间的差别来度量整体的拟合程度.
5 模拟分析
假设模型中含有3个解释变量t1,t2,x.
所估计的模糊光滑函数应该尽可能地接近上述函数.
一共产生25 组样本数据,响应变量的数据构造形式为
yi=g(xi)+1.103 1ti1+0.321 5ti2+rand[-0.5,0.5].
rand[a,b]为在(a,b)区间上的随机数.
本文为了方便构造样本数据,假设模糊输出为对称的三角模糊数,表现形式为(yi,yi-σi,yi+σi)T,其中
σi代表的是观测值的左右扩散,这样形成的25组具有精确输入模糊输出的样本数据如表1所示.
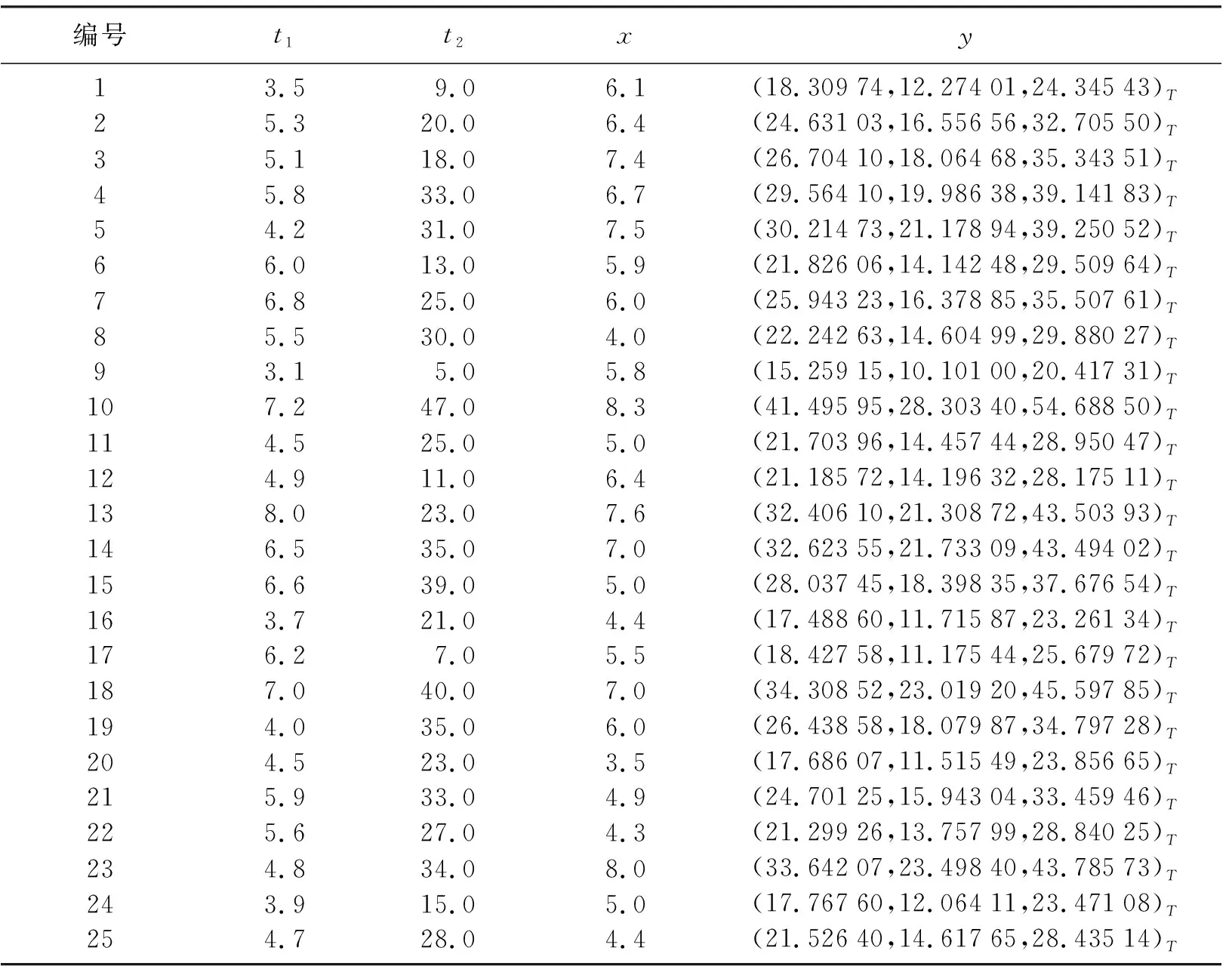
表1 模糊样本数据Table 1 Data of Fuzzy samples


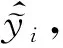
为了评测本文的估计方法,对25组样本数据的拟合度,给出评判标准的计算结果如表2所示.

表2 拟合度的计算结果Table 2 Calculation results of goodness of fit
由表2可见,本文所提出的模型以及两步估计的参数估计方法对模型的拟合程度是比较高的.
6 结 论
本文将经典的半参部分线性模型推广到了具有精确输入、模糊系数、模糊光滑函数、模糊输出的模糊环境下的模糊半参部分线性模型.运用2步估计法对模糊光滑函数以及模糊参数进行估计,为此在模糊环境中采用了局部线性光滑技术对模糊光滑函数进行估计,有效避免了边缘效应的产生;采用基于欧氏距离下的模糊最小二乘方法对模糊系数进行估计.基于以上的2步估计法,成功地推导出模糊光滑函数及模糊系数的显性表达式.采用交叉验证的方法选择最佳带宽,运用的核函数及模糊距离公式在模拟数据集上得到了较好的回归结果.本文提出了评判模型拟合优度的一些标准,模拟分析的结果表明该模型在仿真研究基础上是可靠的,因此为实际研究的发展提供了更加灵活的模型.

