基于观测器Lipschitz非线性系统鲁棒控制方法

孙 延 修

(沈阳工学院 基础课部, 辽宁 抚顺 113122)

随着科技发展,控制系统在现实中的应用越来越广泛.在工业方面,被广泛应用到冶金、化工、机械制造等领域;在军事方面,被广泛应用到航天、航空和航海等领域.伴随控制理论和控制技术的发展,自动控制系统的应用领域还在不断扩大,几乎涉及生物、医学、生态、经济、社会等所有领域.状态反馈控制是以系统状态变量作为反馈量的反馈控制,能够更加有效地针对系统进行控制,被广泛应用于控制系统中.

在实际应用中,存在系统状态变量不易直接测量或只能测量一部分等问题,这给系统状态反馈技术的实现带来了一定的困难,因此基于状态观测器重构系统状态实现状态反馈控制的研究具有重要的意义.近年来针对观测器的研究取得了许多成果[1-5],文献[6]针对广义互联大系统进行了研究,给出了系统区间观测器的设计方法;文献[7]针对不确定系统研究了基于观测器的非脆弱反馈控制问题;文献[8]研究了基于非脆弱观测器的滑膜控制问题.文献[9]针对不确定系统,基于Lyapunov稳定性理论和线性矩阵不等式工具,提出基于观测器的非脆弱鲁棒控制器方法.

本文针对一类Lipschitz非线性系统的鲁棒控制方法进行研究,利用线性矩阵不等式工具,将观测器存在性问题及控制系统渐近稳定问题转换为线性矩阵不等式求解问题,给出了状态观测器与闭环控制系统同时渐近稳定的充分条件,最后通过算例仿真对所提鲁棒控制方法的有效性进行了验证.

1 问题描述

考虑如下非线性系统:

(1)

式中:x(t)∈n为状态向量;u(t)∈m;y(t)∈p分别是系统的输入和输出;Φ(x,t)为满足Lipschitz条件的非线性项;A,B,C均为已知适当维数的常数矩阵.

假设1 非线性项Φ(x,t)满足Lipschitz条件,且

‖Φ(x1,t)-Φ(x2,t)‖≤α‖x1-x2‖,

常数α为Lipschitz常数.

假设2 非线性系统(1)可控且可观测.

引理1[10]若x,y∈n,A,B∈n×n,则对应任意给定的λ>0,如下不等式成立:

2xTABy≤λxTAATx+λ-1yTBTBy.

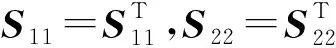
等价于

或

非线性系统(1)的观测器可以设计为:

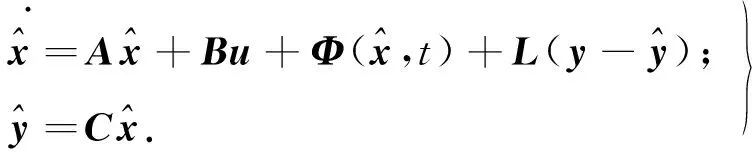
(2)

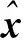
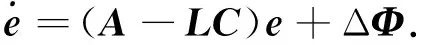
(3)

(4)

根据式(3)和式(4)可以构造如下增广系统:

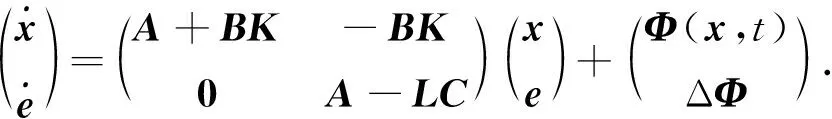
(5)

若增广系统(5)渐近稳定,则可以实现系统(1)基于状态观测器的鲁棒控制.

2 主要结果

定理1 当系统(1)中非线性项Φ(x,t)=0时,若存在对称正定矩阵P∈n×n,Q∈n×n,增益矩阵K∈m×n,L∈n×p,满足如下不等式:

(6)

则系统(1)基于状态观测器(2),可实现鲁棒控制,其中观测器增益矩阵与控制器增益矩阵分别为

L=Q-1CT;K=BTP.

证明 设V=xTPx+eTQe,则有

式中,

令L=Q-1CT,K=BTP则有,

根据引理2知,M<0等价于不等式(6),这时M<0闭环系统渐近稳定,证明完毕.

定理2 若系统(1)中的非线性项Φ(x,t)≠0时,存在对称正定矩阵P∈n×n,Q∈n×n,增益矩阵K∈m×n,L∈n×p,满足如下矩阵不等式:

(7)

则基于状态观测(2)可采用状态反馈控制器,从而实现系统(1)的鲁棒控制,其中观测器增益矩阵与控制器增益矩阵分别为:

L=Q-1CT,K=BTP.

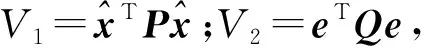
根据假设1和引理1知,

所以,

令L=Q-1CT,K=BTP,则有,

注 定理以线性矩阵不等式(LMI)的形式给出了增广系统渐近稳定的充分条件,既保证了系统状态观测器的存在性,也使得状态反馈闭环系统渐近稳定,达到了基于观测器的鲁棒控制目的,同时给出了增益矩阵的具体形式,避免了观测器及控制器增益矩阵求解的盲目性.

3 数值仿真

考虑非线性系统(1)的参数如下:

通过MATLAB里的LMI工具箱,可以计算出基于观测器的非线性系统状态反馈增益矩阵和观测器的增益矩阵.

1) 当非线性项Φ(x,t)=0时,

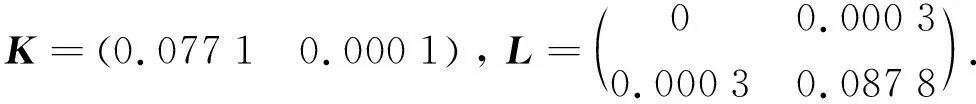
其状态反馈响应曲线如图1所示,状态观测误差曲线如图2所示.

图1 状态反馈响应曲线Fig.1 The response curve of state feedback

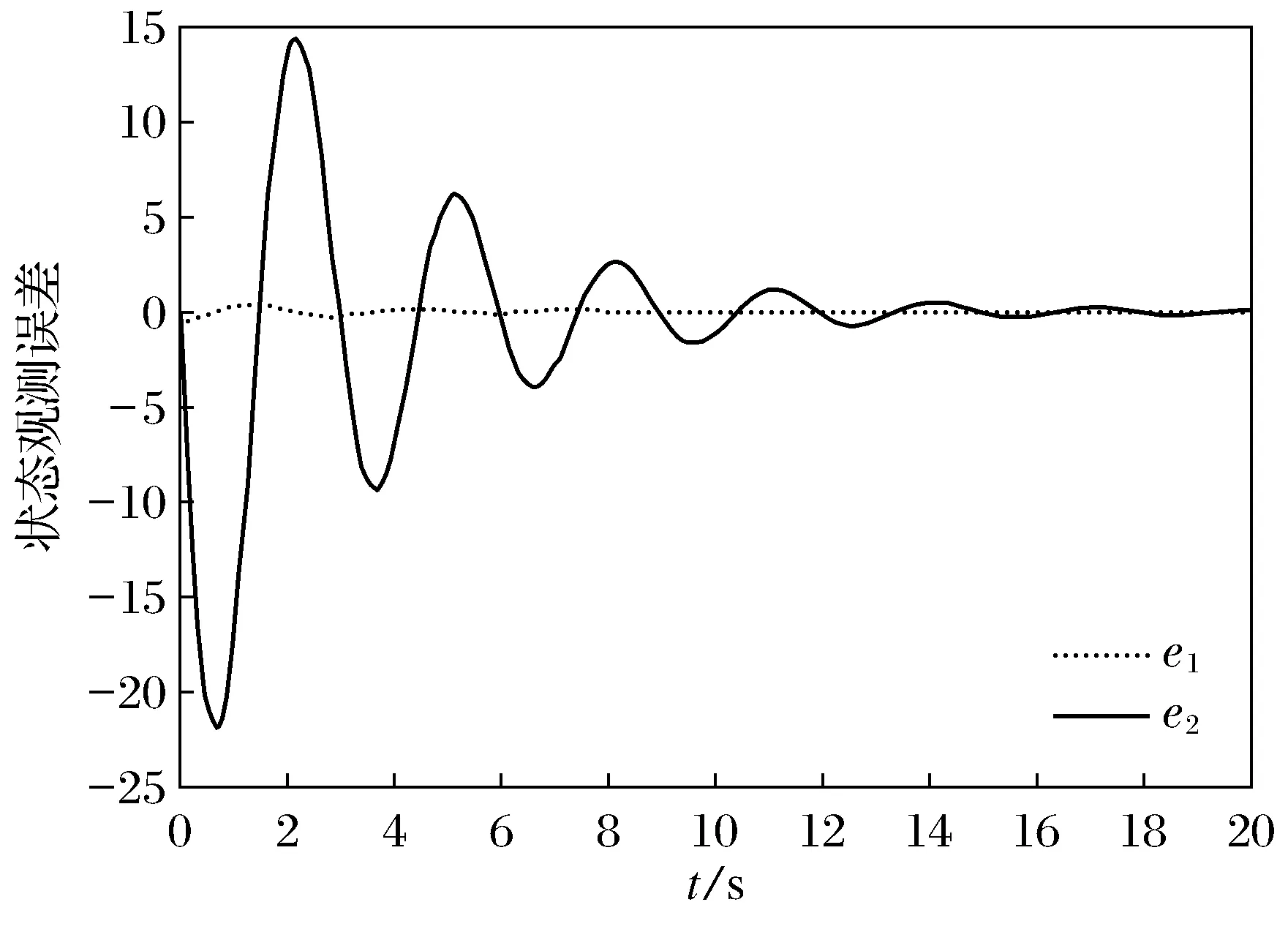
图2 状态观测误差曲线Fig.2 The error curve of state observation

2) 当非线性项Φ(x,t)≠0时,取α=0.2,则可以计算出如下增益矩阵

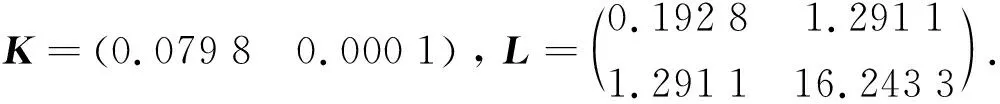
其状态反馈响应曲线如图3所示,状态观测误差曲线如图4所示.

图3 状态反馈响应曲线Fig.3 The response curve of state feedback

图4 状态观测误差曲线Fig.4 The error curve of state observation

由图1～图4可以看出,设计的基于观测器的鲁棒控制器可以使系统在一定的时间内达到稳定,表明了文中所提方法的有效性.

4 结 语

考虑到部分系统状态不易测量等特点,设计了基于状态观测器的鲁棒控制器.以线性矩阵不等式形式给出了系统状态观测器和基于观测器的鲁棒控制器存在的充分条件,并给出了观测器及控制器增益矩阵的具体形式便于求解,最后通过仿真算例证明了基于状态观测器鲁棒控制方法的有效性.