递推归纳法在高中物理习题解答中的应用

汪 鹏

(华东师范大学教师教育学院,上海 200062)

递推是指从已知条件出发,利用特定关系得出中间结论,不断迭代,直到得出最终结果。归纳是从诸多个别的、特殊的事物中,根据一定的逻辑关系,推导出一般性的原理或结论。高中物理习题中有一类问题的解决需要综合运用递推归纳法,此类问题在动力学、动量、粒子偏转等知识点的考查中频繁出现，需要学生具有较高的物理和数学知识水平,较好地考查了学生综合应用知识和方法的能力。

1 递推归纳法的特点

递推归纳法是在类重复的物理情境下,由物理问题所呈现的物理量之间的关系或潜在的物理条件,辅以数学方法来递推归纳,得出物理量变化的通项式,从而归纳出物理量的变化规律，其主要特点如下:

(1) 问题解决的过程需要多次“类重复”的过程,即每一次重复过程均不是上一过程的简单重复,虽有一定的变化,但依然遵循着某些规律；

(2) 解决问题时通过对类重复过程进行3次左右的演算,往往可找到特定的规律；

(3) 在解题技巧上与累加求和、等差、等比数列等数学知识紧密相连。

现以两道习题作为例，说明递推归纳法在高中物理习题解答中的应用。

2 案例分析

例1(2020年全国Ⅱ卷):水平冰面上有一固定的竖直挡板,滑冰运动员面对挡板静止在冰面上,把一质量为4.0kg的静止物块以大小为5.0m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度；物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0m/s的速度与挡板弹性碰撞。总共经过8次这样推物块后,运动员退行速度的大小大于5.0m/s,反弹的物块不能再追上运动员。不计冰面的摩擦力,该运动员的质量可能为( )。

A. 48kg B. 53kg C. 58kg D. 63kg

解析：试题要求经8次推物块后,反弹的物块不能再追上运动员。按照常规思路,需要8次计算才可以得出结果。此过程显然相当复杂繁琐，因为其涉及到类重复运动,可以考虑利用递推归纳法求解问题,通过演算前3次过程,尝试找到规律。

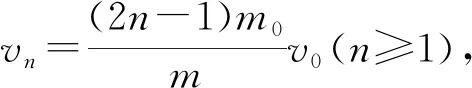
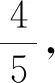
A. 第一次下落的时间与第二次下落的时间之比为5∶4

B. 第二次弹起的高度与第一次弹起时高度之比为4∶5

C. 小球运动的总时间为9s

D. 小球运动的总位移为55m

解析：小球做自由落体运动，与地面发生碰撞,再上弹至最高点,之后一直重复此过程,但小球上升的高度会逐渐减小,这是一个典型的类重复过程，故通过演算前3次的运动过程,可归纳出运动规律。

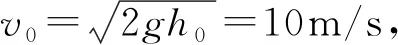
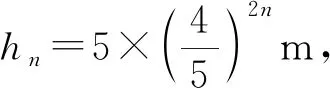
通过上述习题的解决过程,可归纳出此类问题的一般步骤:

(1) 通过对问题情境进行整体分析,把握物理量的特点或运动情况,从中分析出物理量自身的某种相似过程或运动中的相似阶段,即找到类重复过程。在类重复过程中往往具有相同的某一物理量,如运动周期相同、末速度大小相等、位移大小相等。

(2) 通过对上述关键量的分析,并结合题设条件,递推归纳出物理量变化的方式，如等差数列变化、等比数列变化、复合数列变化等，进而写出通项式。

(3) 根据通项式,结合数学中的求和等技巧,问题就可以得到解决。

值得注意的是，归纳递推方法是通过简单过程的归纳而得到通项公式的，需要通过严格的数学归纳进行证明，其正确和科学性才能得到应有的保障。高中物理习题的设计都是命题人员经过理论模型分析后设计的，所以通常不需要进行这方面的证明，但这并不代表递推归纳只是运用上述3步骤就能得到正确的结论。

3 结语

教师在教学中可从“类重复”的特点出发,引导学生挖掘物理量的变化规律,同时加强对学生常用数学技巧方面的训练,则可以让学生较为容易地理解和应用递推归纳法,不仅可以加强学生对于物理概念的理解,更可以提高学生的抽象思维能力。