变截面Euler-Bernoulli梁稳态谐振动的微分求积法研究
夏 雨,葛仁余*,王静平,熊海超,张佳宸
(1.安徽工程大学 建筑工程学院,安徽 芜湖 241000;2.安徽工程大学 汽车新技术安徽省工程技术研究中心,安徽 芜湖 241000)
在工程实际中,梁是很常见的结构之一,如桥式起重机的大梁、火车轮轴、桥梁等,梁的动力特性研究一直是经典而永久的科学问题。对于一般的等截面梁的弯曲问题,材料力学已经给出了结果,但受力复杂的梁以及变刚度梁的计算还是比较繁琐的。一般梁的问题最后都可用梁的近似微分方程表示出来,可归结为两点边值问题。对于平面弯曲梁的静力问题,材料力学当中的结论是通过平面假设及纵向纤维间假设而获得的。而各种假设是会带来误差的,尤其是长高比大于5的短梁,在土木工程中,为了减轻自重和节省材料,经常把刚架和梁设计成变截面和非均匀性的,因而研究非均匀性变截面梁和刚架的强度、稳定和动力学问题无论在理论上还是实际上都是极为重要的。非均匀性变截面梁和刚架,可以归结于一组变系数非正定微分方程,用变分法求解此类微分方程具有一定的困难,用常规方法难以求解。文献[4]直接从微分方程出发推导出单元的刚度矩阵,用普通有限元计算变截面梁和刚架,把梁和刚架划分成许多均匀单元,并用矩阵迁移法来构造单元的刚度矩阵,从而可以提高数值计算精度。文献[5]和文献[6]分别用矩阵迁移法求解了非均匀变截面梁和连续梁的稳定性和自由振动问题。文献[7]用矩阵迁移法解决了非均匀性弹性基础梁的稳定和自由振动问题。文献[8]求解了非均匀变截面梁的稳定和自由振动问题,问题最后归结为求解一个解析表达式的超越代数方程。有关梁的强迫振动问题,人们提出了各种方法来解决。文献[9]和文献[10]采用的是有关振动研究中流行的模态叠加法。模态叠加法是用无穷级数表示解函数,但在无穷级数的实际计算中,不可避免地要用到截断,因此,模态叠加法本质上是一种近似方法。文献[11]研究了机翼在来流作用下的响应,识别了静态和动态分叉区域,评估了阵风对响应的影响,研究了结构非线性变化对机翼响应的影响。文献[12]采用计算机仿真计算方法,对列车通过桥梁时的桥梁动力响应和列车运行性能进行了详细的分析,为三塔悬索桥的动力设计提供了理论依据。利用变量分离法,文献[13]研究了简支梁在匀速运动质量作用下的动力学行为。目前,功能梯度材料板壳的弯曲和振动问题研究与梁类似,主要有基于板理论的解析方法以及有限元方法等。
采用微分求积法(DQM)研究非均匀变截面Euler-Bernoulli梁的稳态谐振动问题,基于Euler-Bernoulli梁理论建立非均匀变截面梁的横向稳态谐振动控制方程,从而将非均匀变截面梁的横向稳态谐振动响应的计算转化为一个变系数常微分方程的两点边值问题。同时,将梁长以等步长均匀分布节点进行离散,边界条件用节点替代法(δ
法)来处理,运用微分求积法求解该常微分方程组,可一次性获得非均匀变截面梁谐振动的振幅及内力。1 变截面梁稳态谐振动的基本理论

图1 受谐振荷载的变截面梁
在工程实际中,尤其是土木或机械工程中,梁承受谐振荷载的情况常常遇到,这时避开共振区一般总是结构设计首先要考虑的问题。当避开共振区时,可以不考虑阻尼的影响,因为阻尼对结构振动的影响很小,所以梁的稳态谐振动的位移和内力的幅值可以直接得出,而不必将振型分解。这样的计算偏于安全,并使问题大大简化,在稳态谐振动时,所有的荷载、变形、内力、支反力和惯性力均按同一简谐规律变化,即同时达到各自的最大值。
长度为L
的变截面Euler-Bernoulli梁如图1所示。基于Euler-Bernoulli梁的基本理论,获得梁的动力响应控制方程为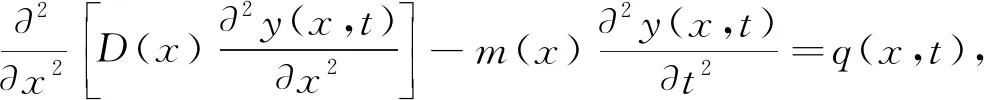
(1)
式中,D
(x
)是抗弯刚度EI
(x
);E
是均匀材料弹性模量;I
(x
)是梁的横截面对中性轴的惯性矩;m
(x
)是梁的单位长度的容重;y
(x
,t
)是梁的位移;q
(x
,t
)是荷载。考虑梁的稳态谐振动问题,则位移y
(x
,t
)和荷载q
(x
,t
)均按同一简谐规律变化,即y
(x
,t
)=y
(x
)cosωt
,(2)
q
(x
,t
)=q
(x
)cosωt
,(3)
式中,y
(x
)和q
(x
)分别为位移幅值和荷载幅值,简称位移和荷载,以下同;ω
为稳态谐振动角频率;t
为时间。将式(2)、式(3)代入式(1),得

(4)


(5)
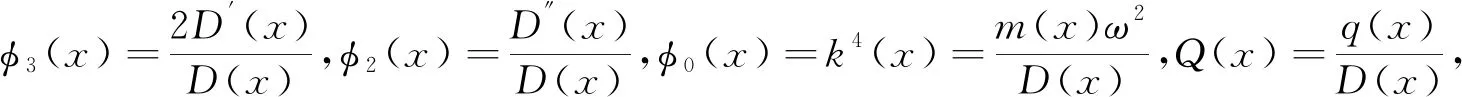
y
(x
)+φ
(x
)y
(x
)+φ
(x
)y
(x
)-φ
(x
)y
(x
)=Q
(x
)。(6)
如果在图1所示的坐标系中,设向上的荷载qcosωt
或Pcosωt
,向上的位移y
(x
)和逆时针方向的转角θ
(x
)为正,反之为负。弯矩Mcosωt
使梁弯成凹形为正,剪力Qcosωt
使梁段顺时针转为正,反之为负,那么存在以下微分关系:
(7)
文中变截面Euler-Bernoulli梁边界条件可以表示为以下常见4种情形:
固支-固支梁的边界条件(C
-C
):向红枣白兰地基酒(42%vol)中加入适量的蒸馏水或无水乙醇,分别配制成20%vol、32%vol、50%vol、63%vol和72%vol的红枣白兰地。
y
(x
)=0,θ
(x
)=0,y
(x
)=0,θ
(x
)=0,(8a)
简支-简支梁的边界条件(S
-S
):y
(x
)=0,M
(x
)=0,y
(x
)=0,M
(x
)=0,(8b)
固支-简支梁的边界条件(C
-S
):y
(x
)=0,θ
(x
)=0,M
(x
)=0,Q
(x
)=0,(8c)
固支-自由梁的边界条件(悬臂梁)(C
-F
):y
(x
)=0,θ
(x
)=0,y
(x
)=0,M
(x
)=0。(8d)
考虑位移函数y
(x
)在梁长区间[0,L
]上可微,将区间[0,L
]上离散单元数划分为n
段n
+1个节点,x
=0,x
=L
,n
+1个节点上函数的导数值可以用节点上函数值的加权线性和近似表示,这里,将位移函数y
(x
)采用拉格朗日(Lagrange)插值函数来描述,即
(9)
这里,l
(ξ
)拉格朗日插值函数其形式为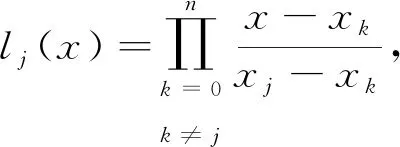
(10)
由式(9)对位移函数y
(x
)求一阶导数,得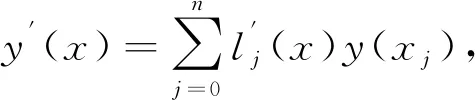
(11)
这里,拉格朗日插值函数l
(x
)的一阶导数形式为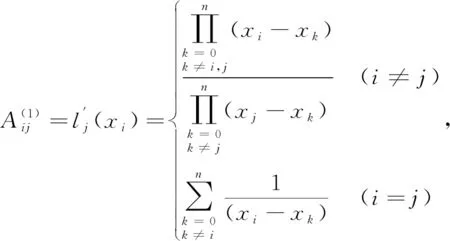
(12)
将式(11) 在梁长区间[0,L
]上离散,从而进一步得到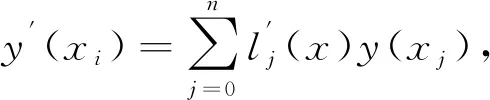
(13)
将式(13)写成向量形式为

(14)

高阶导数顺次地采用低阶导替换,逐步递推可得

(15)
将式(14)和式(15)代入式(6),将式(6)用矩阵和向量形式表示,得
B
y
(x
)=Q
(x
),(16)

将式(5)中的系数用对角矩阵形式表示为
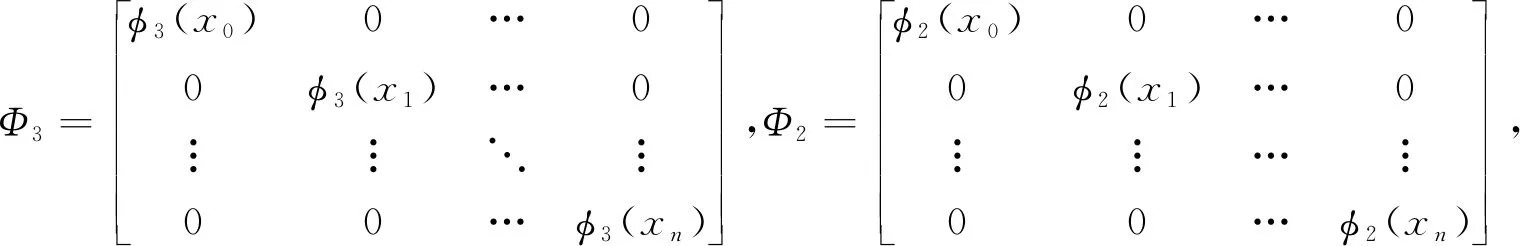

(17)
不失一般性,以非均匀变截面梁固支-固支边界条件为例进行讨论,则相应的边界条件用向量可表示为

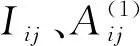

(18)
这里, 由Fortran语言编制通用程序计算,采用高斯主元消去法求解式(18)线性代数方程组获得变截面Euler-Bernoulli梁位移y
(x
),再将其代入式(7)获得相应的转角、弯矩和剪力。2 数值算例与讨论
下面将通过数值算例的分析和比较来讨论微分求积法计算变截面Euler-Bernoulli梁稳态谐振动的可行性和收敛速度,并讨论在不同的激励频率ω
(或者k
)和边界条件下,它们的改变对梁的挠度、弯矩和剪力的影响。2.1 等直截面梁稳态谐振动

图2 受均布谐振荷载的等截面固定-简支梁(C-S)
受均布谐振荷载的等截面固定-简支梁(C
-S
)如图2所示。一长为L
的均匀等直截面梁,梁的左端固支,右端简支,梁的横截面尺寸为:高h
=1.
0,宽b
=1.
0,梁长L
=10,材料的弹性模量为E
=12 000。在区间x
∈[0,L
]上取离散单元数为n
=30时,由微分求积法获得等直截面梁位移、弯矩和剪力的计算值,并和文献[4]计算结果以及精确解同列于表1中进行对比。由表1可知,研究计算值与文献[3]计算结果的两位以上有效数字相同,与精确解3位以上有效数字相同,表明了微分求积法计算等直截面Euler-Bernoulli梁稳态谐振动的精确性。图3、图4分别给出了不同的k
值,在梁长区间x
∈[0,L
]上位移、弯矩的计算值。由图3和图4计算结果可知,当k
=0、k
=0.
1、k
=0.
2、k
=0.
3和k
=0.
5时,梁的位移和弯矩变化平稳。当k
=0.
4时,位移和弯矩急剧增大,这一现象表明了k
=0.
4时,外荷载频率趋于固有频率,梁即将发生共振现象。当k
=0.
5时,区间[0,L
]上离散单元数分别取n
=12、16、20和24时,由微分求积法获得的等直截面梁位移和弯矩计算值如图5和图6所示。计算结果表明,离散单元数取n
≥12时,等直截面梁的位移和弯矩收敛于精确解。
表1 k=0.5时,固定-简支等截面梁位移和内力
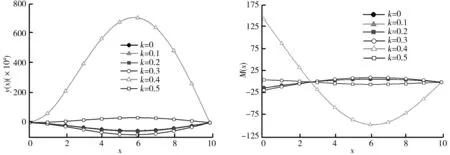
图3 不同k值情况下等直截面梁位移曲线图 图4 不同k值情况下等直截面梁弯矩曲线图
图5 不同n值情况下等直截面梁位移曲线图 图6 不同n值情况下等直截面梁弯矩曲线图
2.2 变截面梁稳态谐振动

图7 受均布谐振荷载的变截面固定-自由梁(C-F)
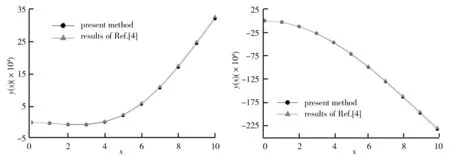
图8 ω≠0情况下变截面梁位移曲线图 图9 ω=0情况下变截面梁位移曲线图
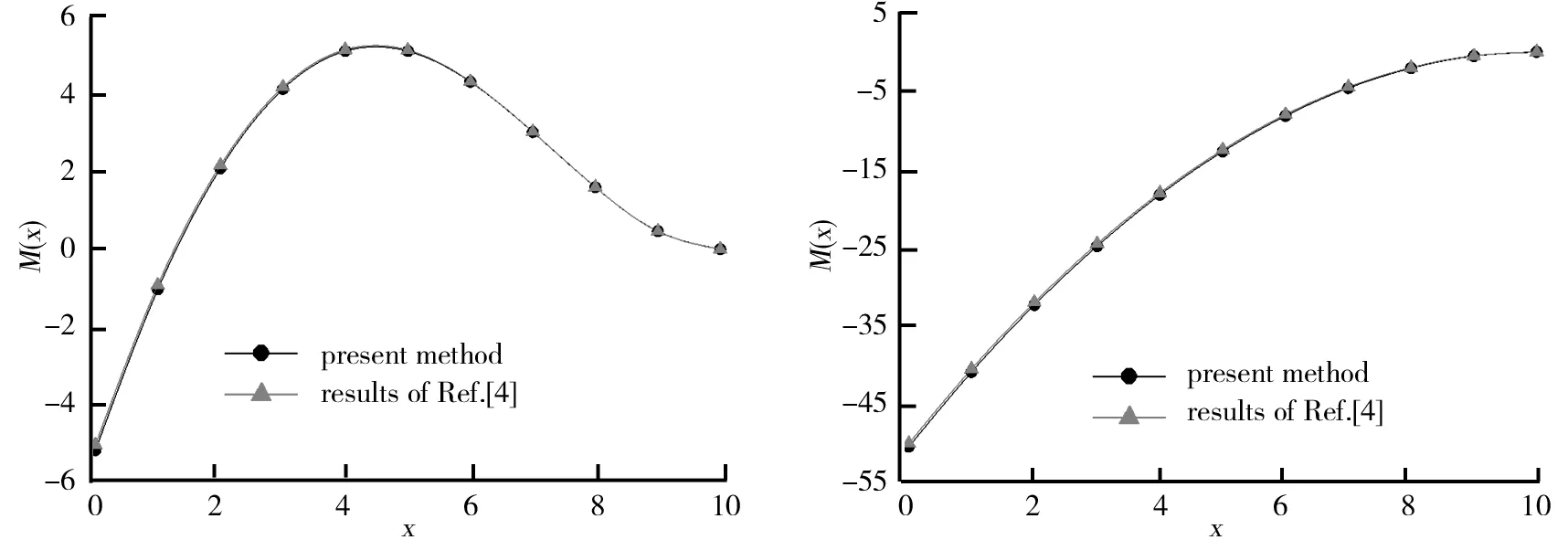
图10 ω≠0情况下变截面梁弯矩曲线图 图11 ω=0情况下变截面梁弯矩曲线图
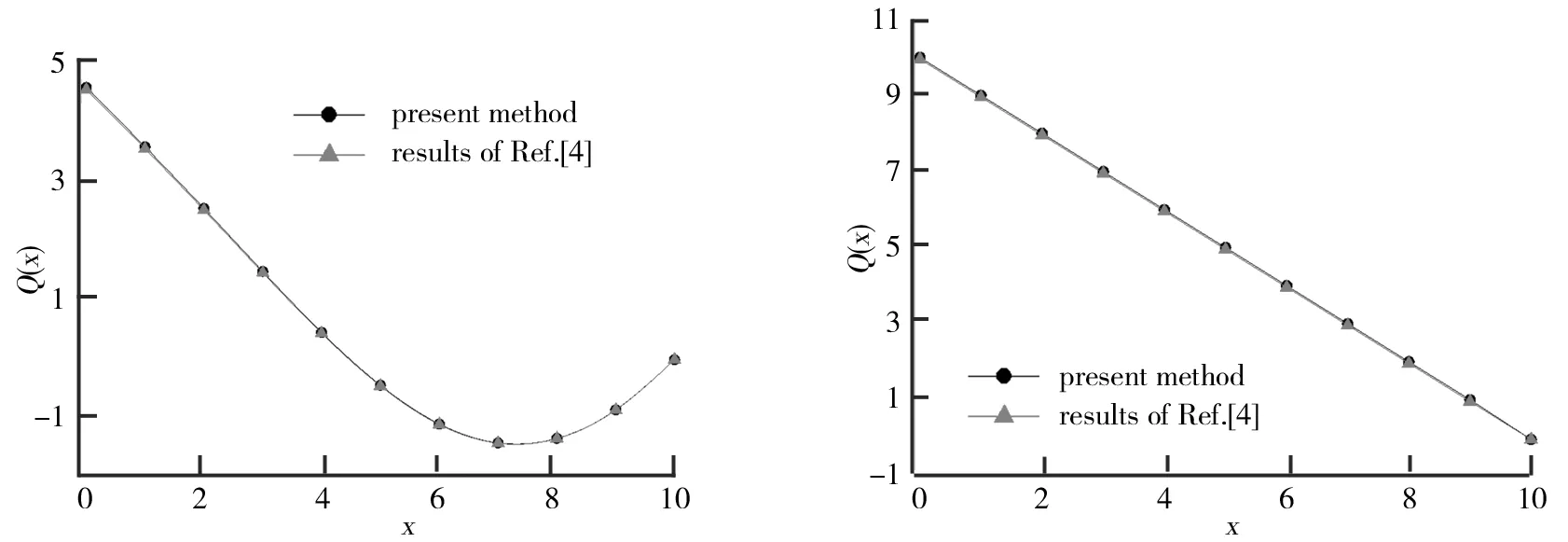
图12 ω≠0情况下变截面梁剪力曲线图 图13 ω=0情况下变截面梁剪力曲线图
图14、图15、图16分别给出了3种不同的边界条件(S
-S
、C
-C
和C
-S
)在梁长区间x
∈[0,L
]上位移、弯矩和剪力的计算值。由图14、图15、图16计算结果可知,当边界条件为S
-S
和C
-C
时,梁的位移和弯矩变化幅度平稳;当边界条件为C
-S
时,位移、弯矩和剪力幅度急剧增大,这一现象表明了边界条件为C
-S
时,激振力频率趋于该变截面梁的固有频率。
图14 3种不同边界条件下ω≠0时的变截图15 3种不同边界条件下ω≠0时的变截 面梁位移曲线图 面梁弯矩曲线图
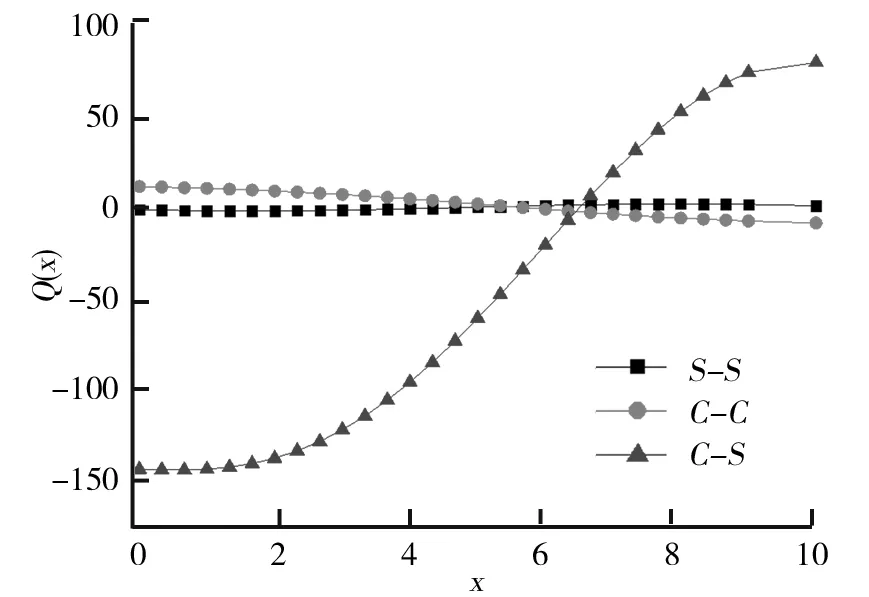
图16 3种不同边界条件下ω≠0时的变截面梁剪力曲线图
3 结论
研究采用微分求积法研究非均匀变截面Euler-Bernoulli梁的稳态谐振动问题,基于Euler-Bernoulli梁理论建立非均匀变截面梁的横向稳态谐振动控制方程,从而将非均匀变截面梁的横向稳态谐振动响应的计算转化为一个变系数常微分方程的两点边值问题。运用微分求积法对其进行数值计算,讨论了4种边界条件情况下等截面梁和变截面梁的位移和内力的计算,获取了轴向功能梯度变截面Euler-Bernoulli 梁自由振动前若干阶固有频率。研究主要结论如下:
(1) 微分求积法通用性好、适应性强,且计算精度高。它对未知函数采用多项式逼近,保证了解函数及其导数值的光滑连续,可一次性地计算出变截面梁的位移及内力,并与精确解、已有文献计算结果吻合良好,表明了微分求积法分析梁的稳态谐振动问题的可行性和精确性。
(2) 微分求积法分析等截面梁和变截面梁稳态谐振动时,通过梁的位移、弯矩和剪力等物理参量的急剧增大这一现象,可以定性判定梁的共振频率范围。
(3) 研究方法分析等截面梁和变截面梁稳态谐振动时,对材料和截面几何性质函数的具体形式无需任何限制条件,同时,研究方法避免了用迭代方法计算超越方程的困难和繁杂,可以进一步推广应用于一般梁的瞬态动力响应的分析研究中。

