一种用于无人车路径规划的改进双向快速扩展随机树算法研究

刘光中,时培成*,倪 璇，梁涛年

(1.安徽工程大学 汽车新技术安徽省工程技术研究中心，安徽 芜湖 241000；2.芜湖伯特利汽车安全系统股份有限公司，安徽 芜湖 241009)

智能交通系统的兴起给汽车工业的发展带来新的活力，在智能交通系统发展过程中，最核心的部分就是无人驾驶车辆。路径规划作为无人驾驶汽车发展研究的关键技术之一，受到广泛的关注和研究。路径规划过程就是车辆根据车身传感器所接收到的信息，在即将行驶的环境空间中分析计算出一条既满足车辆动力学又满足几何约束，又能在行进过程中不与障碍物发生碰撞的可行轨迹。

近年来基于快速扩展随机树(Rapidly Expanding Random Tree，RRT)的路径规划方法由于在高维空间中的卓越性能受到了广大学者的青睐。该算法虽然本身具有概率完备性，且算法收敛速度较快，在具有障碍物的未知环境中可以很好地应用等优点，但也存有一些不容忽视的缺点：①为了找到可行路径，算法通过不停地进行反复迭代来探索全部的未知环境，计算过程中会消耗大量的内存；②由于算法在环境空间中进行扩展生长时采样比较随机，导致随机树在路径生成时没有方向，规划结束时会难以生成最优路径；③由于算法的随机性，会很大程度上计算出较为粗糙弯折的路径，不适合无人车辆直接使用。

针对RRT算法所存在的不足，研究人员有针对性地做出了一些改进。Adiyatov O等提出的RRT算法，巧妙地解决了RRT算法中难以生成最优路径的问题，但是会增加很大的计算量，使得路径生成实时性大幅度降低。裴以建等在RRT的基础上，提出一种新的离线路径规划算法，结合人工势场法调整采样区域，缩短了生成最优路径的时间。康亮等提出的将滚动窗口和RRT相结合的算法，以滚动方式进行在线规划，提高了算法对未知空间的探索能力，但是效率偏低。潘思宇等在RRT算法的基础上进行了改进，同时引入节点启发式采样函数，在一定程度上提高了路径规划时的速度和质量。闫明亮等提出了一种新的采样方法，提高了路径规划的效率，但是仍不能很好地解决采样点随机性较大的问题。

针对上述问题，研究提出一种新的改进Bi-RRT算法，在原始的RRT算法基础上替换了原算法的采样方式，同时生成两个随机采样点，选择两者中距离目标点比较靠近的采样点，以提高采样效率，并加入目标引力思想，让随机树更具有方向性；规划过程中，两棵树将对方新生节点作为目标点，在提高方向性的同时，降低不必要节点的产生。通过对RRT和Bi-RRT算法进行仿真实验验证，表明研究算法拥有更小的时间代价、更少的迭代次数和更高的路径质量。

1 基本RRT算法

1.1 单向RRT算法

RRT算法是一种采用增长式扩展树的搜索算法，流程如图1所示。它将所要规划路径的起点位置作为随机树的根节点，将终点位置作为随机树的目标节点。随机树从根节点出发，在空间中随机采样，使用随机采样函数生成随机点，然后用最近点函数遍历随机树中所有已生成节点，找到距离随机树中最近的节点，接着从最近点向随机点方向扩展一个步长生成一个新的节点。通过碰撞检测函数来判断最近点向新节点扩展过程中是否与障碍物发生碰撞，若无碰撞，将新节点加入随机树中，反之，舍弃此新生节点，继续重新采样。直至新生节点与目标节点间的距离小于设定阈值，停止生长，返回规划的路径。

图1 基本RRT算法

1.2 双向RRT算法

双向RRT算法(Bi-RRT)的扩展示意图如图2所示。Bi-RRT在自由空间中定义了两棵树，采用和基本RRT算法相同的节点生成方式，算法从起始点位置和目标点位置各生成一棵随机树相向扩展，根据产生的单个随机点，两棵树交替扩展生成新节点，直到两棵树相遇或者新生节点间距离小于设定阈值则生成路径。

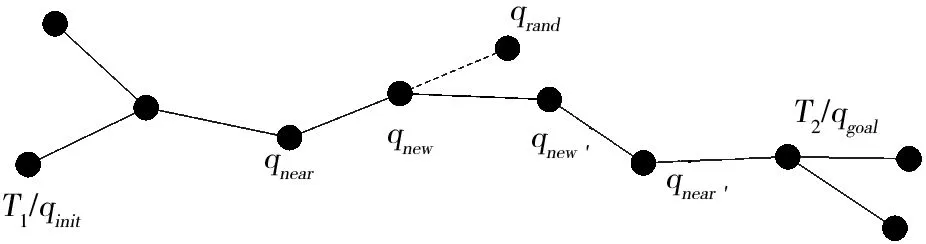
图2 Bi-RRT扩展示意图

2 改进Bi-RRT算法

2.1 节点生成方式的改进与自适应概率采样目标偏向策略

基本RRT算法节点生成方式单一，且生成的节点比较随机，导致随机树扩展时没有方向，降低了规划速度。研究提出双采样点的方式来提高算法的搜索效率，在环境空间内同时生成两个随机采样点，通过比较两个采样点到目标点的距离，选择与目标点较近的点作为临时采样点，能够快速减少待规划路径，缩短算法运行时间。

同时，针对算法的无方向性、容易陷入局部极小值问题，提出基于目标偏向的自适应概率采样策略，目标引力思想可以使随机树的生长具有一定的方向性。改进Bi-RRT算法采用启发式采样，运行时通过随机概率

p

(1>

p

≥0)来选择扩展点。若设定参照概率

p

，当

p

<

p

时，选择随机点作为最终采样点，当

p

>

p

时，选择目标点作为最终采样点，当目标点作为采样点时能够提高随机树的扩展效率。扩展树节点

q

时，计算公式为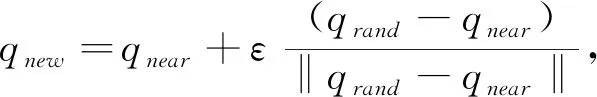

(1)

式中，

ε

为扩展时随机树的步长;(

q

-

q

)表示两向量单位化;||

q

-

q

||表示两点间欧氏距离。加入目标引力思想的

q

计算公式为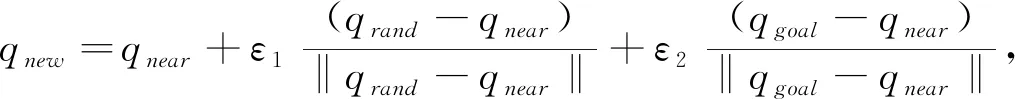

(2)

式中，

ε

表示向随机采样点方向扩展时的步长；

ε

表示向目标点方向扩展时的步长；||

q

-

q

||为

q

和

q

间欧氏距离。上述目标偏向引力思想虽然可以引导随机树向目标方向生长，但是选取目标点作为随机点的概率值是固定的，当算法陷入局部极小值时，向着目标扩展一般是无效的，反而会浪费大量的计算内存。因此，当以目标点方向扩展无效时，认为扩展树陷入局部极小值，将概率

p

值设为0，让算法努力通过随机生长来逃出局部极小值，之后随着随机采样次数增多，随机树跳出局部极小值的可能性逐渐变大，所以

p

值也会随着扩展次数的增加而增加。随机树跳出局部极小值时的

p

值公式如下：

(3)

式中，

p

是未陷入局部极小值时的概率；

c

是形状系数；

n

是最大尝试次数。当

n

接近

n

时，

p

逐渐恢复为

p

。

2.2 改进Bi-RRT算法原理

本算法将起始位置

q

和目标位置

q

分别作为

T

、

T

两棵随机树的根节点，两棵树进行相向生长，如图3所示。

T

生长时，使用采样Random_point函数同时生成两个随机采样点

q

1、

q

2，用Near_to_Goal函数比较

q

1、

q

2与目标点位置

q

的距离。若知|

q

1，

q

|<|

q

2,

q

|，选择距离较小的

q

1作为临时采样点，结合目标引力思想，当

p

<

p

时，选择

q

作为最终采样点，当

p

>

p

时，选择

q

作为最终采样点来扩展得到新节点

q

。

T

扩展时，将

T

生成的新节点

q

作为目标点，新节点产生方式与

T

相同。接下来两棵树分别把对方上一步新生成的节点作为目标点，继续向下扩展生长，一直到两棵树的新生节点间的距离小于设定步长，则连接两节点生成规划路径。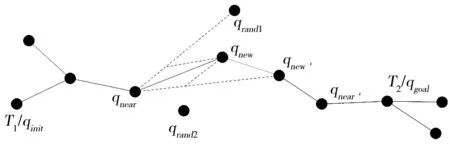

图3 改进Bi-RRT算法示意图

2.3 改进Bi-RRT算法实现

提出的改进Bi-RRT算法实现过程如图4所示。

(1)分别以起始位置

q

和目标位置

q

为

T

、

T

根节点，两棵树相向生长。(2)使用采样Random_point函数同时生成两个随机采样点

q

1、

q

2，用Near_To_Goal函数选择距离目标较近点作为临时采样点。(3)结合目标引力思想，当

p

<

p

时，选择

q

作为最终采样点；当

p

>

p

时，选择

q

作为最终采样点。新生节点

q

会偏向最终采样点。(4)通过碰撞检测Collision Free函数来判断节点

q

向节点

q

扩展过程中是否与障碍物发生碰撞，若无碰撞将

q

加入

T

中，反之，返回第(2)步。(5)

T

、

T

分别把对方上一步新生成的节点当作目标点，进行下一步生长。(6)两随机树新生节点

q

间的距离小于设定步长，则生成路径。

图4 改进Bi-RRT算法流程图

3 仿真验证

为了验证改进Bi-RRT算法的有效性、实时性和相对原始算法的优越性，绘制了复杂障碍物地图和迷宫地图如图5所示。由图5a可见，障碍物大小不一、形状不规则且分布复杂，是为了充分模拟现实中复杂的环境。由图5b可见，障碍物形状规则，但是通路较多极具迷惑性，对算法的计算能力是一种极大的考验。在这两种环境地图中进行传统RRT和Bi-RRT算法仿真，并对规划路径及规划效率作出对比分析。

仿真实验均在Matlab R2015a编程环境下，电脑配置参数：CPU，Intel(R) Core(TM)i7-6700，3.4 GHz；运行内存为4 G。地图尺寸大小为500*500，起始位置和目标位置坐标分别为[10,10]，[490,490]。

图5 环境地图

3.1 复杂障碍物地图仿真分析

在图5a中，将RRT算法同Bi-RRT算法和改进Bi-RRT算法分别运行30次，将3种算法在每次路径规划中产生的迭代次数、规划时间和路径长度记录下来。各取3种算法的一次运行结果如图6所示。由图6可知，基本RRT算法因为具有概率完备性，在地图中采用均匀随机采样策略，搜索盲目，无目的性，故产生了大量的无用节点，且路径比较曲折；Bi-RRT算法相对RRT算法，采用两棵树相向生长的方法来提高探索速度，很大程度上减少了无用的节点；改进Bi-RRT算法相对前面两种算法，减少了极大部分的无用节点，生成的路径在三者中最优。3种算法在复杂障碍物地图中成功搜索到路径时迭代次数、所需时间和路径长度的对比图如图7、图8、图9所示。

图6 复杂障碍物地图规划比较

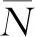
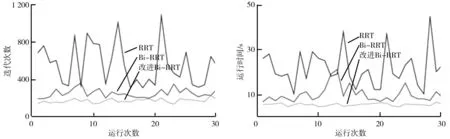
图7 复杂障碍物地图迭代次数对比 图8 复杂障碍物地图运行时间对比

图9 复杂障碍物地图路径长度对比

3.2 迷宫地图仿真分析

在图5b中，将RRT算法同Bi-RRT算法和改进Bi-RRT算法各自运行30次，记录3种算法在每次路径规划中的迭代次数、规划时间和路径长度。3种算法的运行结果图如图10所示。由图10可知，基本RRT算法在整个环境地图上生成了大量的无用节点，路径极其曲折，不够平滑；Bi-RRT算法相对RRT算法，节点明显减少，路径弯折情况有所改善；改进Bi-RRT算法相对前两种算法，所产生的无用节点数量最少，路径最平顺。3种算法在迷宫地图中成功搜索到路径时迭代次数、所需时间和路径长度的对比图分别如图11、图12、图13所示。由图11、图12、图13可知，改进Bi-RRT算法相对于基本RRT算法和Bi-RRT算法，在算法迭代次数、路径规划时间和规划路径长度上具有明显优势。

3个参数记录值的平均值如表2所示。由表2中数据计算得出，改进Bi-RRT算法相对基本RRT算法和Bi-RRT算法，在平均迭代次数上，分别减少了73.8%，21.7%；在平均规划用时上，分别缩短了81.2%，46.7%；在平均路径长度上，分别降低了14.2%，7.7%。

表1 复杂环境地图仿真实验数据

表2 迷宫地图仿真实验数据

图10 迷宫地图规划比较

图11 迷宫地图迭代次数对比 图12 迷宫地图运行时间对比

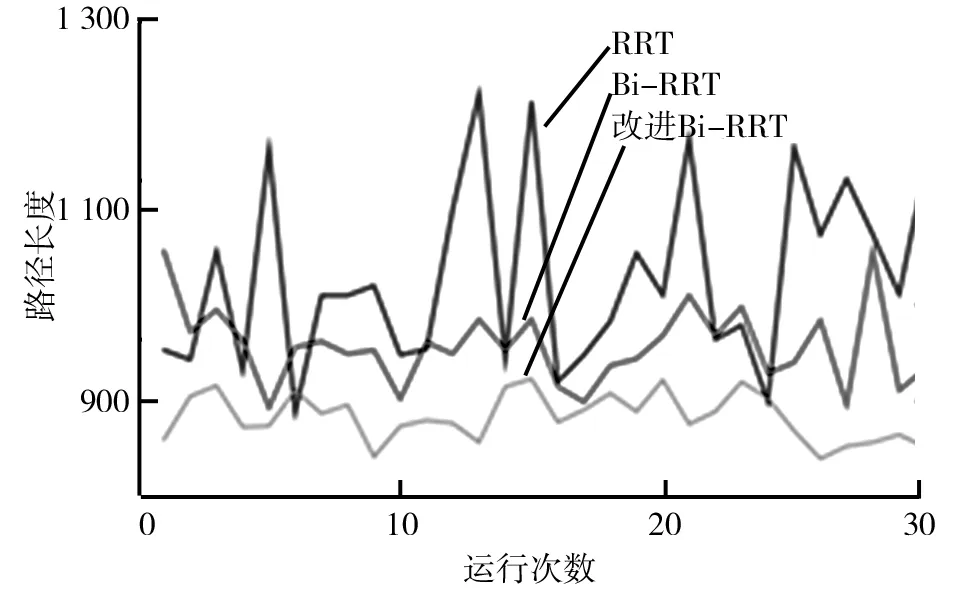
图13 迷宫地图路径长度对比

4 样车实验

为了验证改进算法的可靠度，进行了样车实验如图14所示。样车配备了16线激雷达和单线激光雷达，两种雷达可获取融合后更为精确的环境信息。导入改进Bi-RRT算法后，由工控机对环境进行处理，并规划出路径。

图14 样车及主要部件

在获取环境信息建立地图模型后，改进的Bi-RRT算法规划出的行驶路径如图15所示。运行过程如图16所示。由图16可知，在布置好的环境地图中，小车从起始位置成功穿越障碍物到达终点，验证了改进Bi-RRT算法所规划路径的可靠性。

图15 规划路径展示

图16 运行过程展示

5 结论

研究以传统RRT算法为基础，对Bi-RRT算法做出了一些改进。摒弃单个采样的方法，同时生成两个随机采样点，选择两个随机点距离目标点较近的点作为采样点，提高了采样效率和采样点的有效性；又结合目标引力思想来选择最终采样点，可使得路径在生长过程中具有明显的方向性，提高算法规划最优路径的效率；在算法运行过程中，通过选择对方随机树生成的最新节点作为目标点，加快了路径生成速度。在两种环境地图中对改进后的Bi-RRT算法进行仿真验证，结果表明，改进Bi-RRT算法在迭代次数、路径生成所需时间和路径长度上相较于RRT、Bi-RRT两种算法具有明显优势。样车在搭建的实验场景中成功规划出了可行路径，验证了改进Bi-RRT算法的可靠性。