基于激光雷达数据的森林蓄积量模型反演及精度估算

刘 海，苏本跃

(1.安庆师范大学 计算机与信息学院，安徽 安庆 246133；2.国家林业和草原局华东调查规划设计院，浙江 杭州 340019)

森林是陆地生态系统中的重要组成部分，具有巨大的固碳功能，并且在维护生态安全、应对气候变化中发挥着特殊作用。蓄积量是林业调查中的一项重要指标，它能够衡量森林资源的丰富程度以及健康程度，也直接反映了森林的经营成效。遥感技术已被广泛应用于各个领域，而林业遥感技术作为其中一个不可或缺的组成部分，不仅可以获取林业资源管理的数据，更能进一步揭示林业经营管理的生态影响。定量遥感是指在基于模型知识的基础上，依据可测参数值去反推目标值，这一过程也被称作为模型反演。激光雷达等遥感数据应用于森林测树因子的定量估测反演一直是林业科研的主要方向。双重抽样是以一个大样本估测权重，用一个较小的样本估测蓄积量，采用误差估计方法来计算两重样本估测精度的算法。研究主要是利用激光雷达点云数据进行森林蓄积量反演，构建反演模型，并通过优化两重抽样算法，形成基于两步回归估计的森林蓄积量反演结果与人工验证结果的精度估算。

1 森林蓄积量反演的遥感估测

1.1 森林蓄积量反演的一般步骤

在森林蓄积量反演的遥感估测方法中有两个重要的中间环节。一是特征提取。被动光学图像(可见光、多光谱、高光谱)主要是提取光谱特征，与冠幅有关的冠幅大小、形状、闭合度等，以及纹理特征，而LiDAR主要提取单木的三维冠层结构特征、点云强度特征，组成特征向量集；二是反演模型的选择。多元逐步回归和随机森林是近些年来频繁使用的分类器，森林蓄积量的遥感估测基本流程如图1所示。研究主要侧重于遥感估测的模型反演与反演结果的精度计算，因此,具体激光雷达数据的获取及处理暂不在研究研讨的范围之内。

图1 森林蓄积量的遥感估测基本流程

1.2 森林蓄积量反演常用的两重抽样验证方法

人工判读数据与地面验证数据，一般应按双重回归抽样(也称二相回归抽样)计算。人工判读的数据用

z

表示，实地调查的用

y

表示，回归方程为

y

=

α

+

βz

+

ε

,

(1)

小班平均蓄积估计为

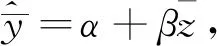
(2)

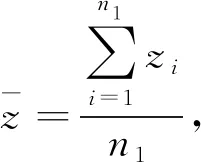
(3)

总体蓄积总量估计为

(4)

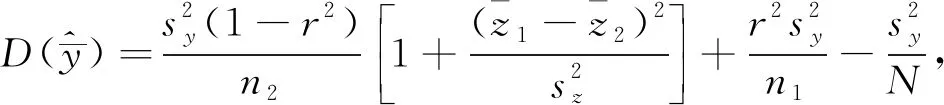
(5)

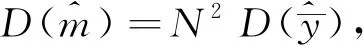
(6)

估计值的误差限为

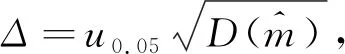
(7)

大样本时

u

005可取1

.

96。估计精度为

(8)

2 森林蓄积量反演及反演模型评价

2.1 森林蓄积量反演的常用模型

系统整理分析现有森林参数反演方法，目前基于LiDAR信息反演森林生物量或蓄积量的各类建模方法，较为适合广域范围尺度，估测精度较高的主要有随机森林和多元线性回归等反演模型。

(1)随机森林模型。随机森林模型可以看作是决策树模型的一个升级，而决策树模型是一种基于有监督的机器学习算法的数学模型。其基本思想首先是从根节点开始，对实例的某一特征值进行测试，然后根据测试结果将实例分配到其子节点，此时每个子节点都对应着该特征的一个取值，如此递归地对实例进行测试并分配，直到到达叶节点，最后实例就被完全分到叶节点的类中。随机森林模型对样本进行了重采样，并且对特征也进行了随机选取，形成多棵树，再通过投票的方式决定数据分类。

(2)多元线性回归模型。多元线性回归是森林蓄积量遥感估测的常用算法，其主要思想是利用线性回归方程的最小平方函数对多个自变量和因变量之间关系进行建模的一种回归分析。这种函数为带有多个回归系数的模型参数的线性组合，其模型公式为

y

=

β

+

β

x

+

β

x

+…+

β

x

+

ε

,

(9)

式中，

y

为因变量;

β

、

β

、…、

β

为参数;

x

、

x

、…、

x

为自变量;

ε

为误差。

运用在估计中，公式就变成

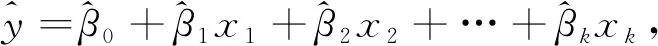
(10)

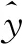
采用最小二乘法估计，即求

(11)

在建立回归模型时，需要对自变量进行选择，一般采用显著性检验的方法对统计量进行筛选，其主要流程是：将一个或一个以上的自变量引入回归模型中时，是否使残差平方和(

SSE

)显著减少。如果增加一个自变量使残差平方和(

SSE

)显著减少，则说明有必要将这个变量引入回归模型中，否则，没有必要将这个变量引入回归模型中。确定在模型中引入自变量

x

是否使残差平方和(

SSE

)显著减少的方法，就是使用

F

统计量的值作为一个标准，以此来确定在模型中增加一个自变量，还是从模型中剔除一个自变量。变量选择方式分为三种：①向前选择。第一步：对

k

个自变量分别与因变量

y

的一元线性回归模型，共有

k

个，然后找到

F

统计量的值最大的模型及其自变量

x

并将其首先引入模型。第二步：在已经引入模型的

x

的基础上，再分别拟合

x

与模型外的

k

-1个自变量的线性回归模型，挑选出

F

值最大的含有两个自变量的模型，依次循环、直到增加自变量不能导致

SSE

显著增加为止。②向后剔除。第一步：先对所有的自变量进行线性回归模型。然后考察小于

k

个去掉一个自变量的模型，使模型的

SSE

值减小最少的自变量被挑选出来从模型中剔除。第二步：考察

p

-1个再去掉一个自变量的模型，使模型的

SSE

值减小最少的自变量被挑选出来从模型中剔除，直到剔除一个自变量不会使

SSE

值显著减小为止，这时，模型中所剩自变量自然都是显著的。③逐步回归。在向前选择的基础上，当引入一个变量后，首先查看这个变量是否使得模型发生显著性变化(

F

检验)，若发生显著性变化，再对所有变量进行

t

检验。当原来引入的变量由于后面加入的变量的引入而不再显著变化时，则剔除此变量，确保每次引入新的变量之前回归方程中只包含显著性变量，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，最终得到一个最优的变量集合。

2.2 森林蓄积量反演模型的构建及模型评价

研究采用安徽省2019年金寨等9县(市)LiDAR反演森林蓄积量试点项目的激光点云数据及785个样地数据进行建模。从LiDAR数据中计算提取46个与高度相关的、10个点云密度相关的及42个与强度相关的，共计98个统计变量，参与建模。

模型的评价和检验是评价模型好坏的关键工作，研究在评价LiDAR森林蓄积量模型时，将调整确定系数(

adjR

)、估计值的标准差(

SEE

)、均方根误差(

RMSE

)、相对均方根误差(

rRMSE

)4项指标作为基本评价指标，计算公式如下：

(12)

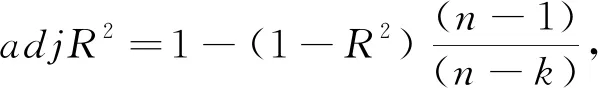
(13)

(14)

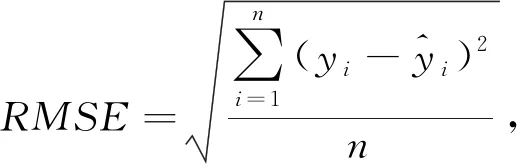
(15)

(16)

不同的精度估测方法会从不同的角度采用不同的参数反映反演结果的优劣。一般情况下，

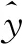
adjR

表示根据自变量的变异来解释因变量的变异部分，

adjR

值越接近于1，估测值与真实值的拟合情况越好。

RMSE

是均方误差的平方根，用来衡量预测值与真实值之间的误差情况；

rRMSE

是无量纲统计指标，反映模型精度情况，通常

rRMSE

<10%表示模型精度非常好，10%<

rRMSE

<20%表示模型精度较好，20%<

rRMSE

<30%表示模型精度一般，

rRMSE

>30%表示模型精度较差。

考虑到模型反演的结果(由于不同模型得到的评价指标并不完全相同，所以比较各算法模型的指标不是上文中的全部指标)、运行速度以及可解释性的强弱，研究最后采用多元逐步回归的方法，两者的比较如表1所示。

表1 两种算法的adjR2及运行时间比较

根据安徽省森林资源状况及地形地貌，分地形分树种建立13个蓄积量估测模型：柏木、平原阔叶纯、平原阔叶混、丘陵阔叶混、丘陵杉类、丘陵松类、丘陵针阔混、山区阔叶纯、山区阔叶混、山区杉类、山区松类、山区针阔混、杨。研究中建模过程都在Spss Modeler上进行，硬件环境为Intel®Core(TM)i9-9900K 3.6 GHz CPU，64 G内存；操作系统是Windows 10。建模过程中采用随机分组10次10折交叉验证方法确定最优模型参数。各模型通过0

.

05置信水平的显著性检验，变量无自相关性，

VIF

均小于10，不存在多重共线性。具体模型结构及评价指标如表2所示。从表2中可以看出,LiDAR反演蓄积结果拟合度相对较好，调整决定系数在0

.

53～0

.

93之间，平均决定系数约0

.

74，均方根误差

RMSE

在(0

.

58～2

.

77)立方米

/

亩，均值1

.

6 立方米

/

亩；相对均方根误差

rRMSE

在(0

.

15～0

.

48)范围内，均值0

.

32，达到当前公认研究水平(0

.

2～0

.

4)。

表2 安徽省十区县点云密度不足1个每平米的模型结构及评价指标

3 基于两步回归估计的森林蓄积量反演与人工验证结果精度估算

在遥感反演森林蓄积量的过程中都会涉及到反演精度的估算，而在广域范围的实际生产应用过程中，为了获得更为良好的成果，往往除了使用遥感反演以外，都会匹配相应的人工验证，因此，结合人工验证结果计算精度也是值得探讨的问题。

3.1 人工验证样本

为了验证安徽省2019年金寨等9县(市)LiDAR反演森林蓄积量的精度，采集了两重验证样本：第一重样本为利用高清遥感影像、2014年森林资源规划设计调查成果、2016年LiDAR反演得到的森林蓄积及2019年LiDAR反演得到的森林蓄积等数据源，进行人工修正，获得修正后乔木林小班蓄积；第二重样本分山区、丘陵和平原三种类型，依据《安徽省森林资源规划设计调查实施细则》，实地调查采集乔木林小班的林分相关因子，再由每公顷蓄积计算出小班蓄积。两重样本采用两步回归估计方法，计算金寨等9县(市)LiDAR反演乔木林蓄积的精度和估测区间。

(1)人工基于多源数据的修正样本。修正样本利用高清遥感影像、2014年森林资源规划设计调查成果、2016年LiDAR反演蓄积及2019年LiDAR反演蓄积等数据源，进行人工修正后获得。人工修正乔木林小班总数31 659个，占乔木林小班总数254 086的12.46%，其中，平原修正10 791个，丘陵修正3 439个，山区修正17 429个。经过修正，在乔木林小班中有1 610个小班实际为非林地或无林地，占验证小班数的5.09%。

表3 人工修正乔木林小班数统计表

(2)人工基于现地验证的修正样本。为验证2019年金寨等9县(市)LiDAR反演乔木林蓄积的估测精度，按照平原、丘陵、山区三种类型，在人工修正小班中抽取部分乔木林小班开展现地验证。现地验证乔木林小班总数5 560个，其中，平原验证1 876个，丘陵验证1 655个，山区验证2 029个。现地验证小班总数占乔木林小班总数的2.09%，占人工修正乔木林小班数的17.56%。

表4 现地验证乔木林小班数统计表

3.2 基于两步回归估计的估测方法

因为双重回归抽样估计法不能利用全覆盖的激光雷达数据信息，为了充分利用人工修正和现地验证两重样本，对LiDAR反演蓄积估测区间和精度进行估测，所以采用改进的两重回归估计——两步回归估计方法：①通过在人工修正数据与LiDAR反演蓄积数据之间建立第一重样本的回归模型，计算人工修正数据估计值;②通过建立现地读数据与第一重样本之间的回归模型，计算总体LiDAR反演乔木林小班的蓄积估计值;③两重样本之间采用双重回归估计公式，获得LiDAR反演蓄积总体的估测区间和精度。

(1)人工修正数据与LiDAR反演蓄积数据之间的回归。利用具有人工修正乔木林小班数据为因变量

z

，对应的LiDAR反演蓄积数据为自变量

x

，建立回归方程

z

=

a

+

bx

+

ε

,

(17)

其估计形式为

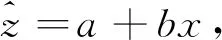
(18)

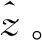
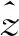
(19)

其估计形式为

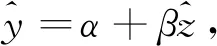
(20)

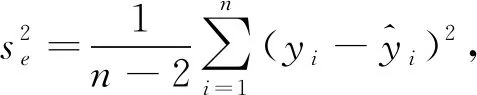
(21)

式中，

n

为现地验证小班数，即参与建立回归模型(3)的小班数量，计算参数的方差矩阵。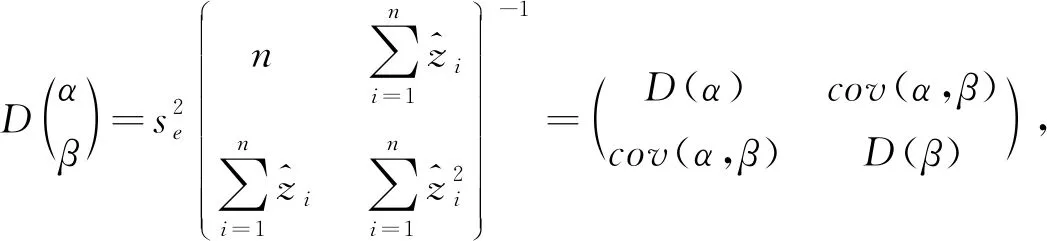

(22)

式中，

D

(

α

)、

D

(

β

)分别为参数

α

、

β

的方差;

cov

(

α

,

β

)为参数之间的协方差。根据式(12)计算出总体LiDAR反演乔木林小班的蓄积估计值。这里的

cov

(

α

,

β

)均为用式(10)计算得到的估计值。

(3)LiDAR反演乔木林总体蓄积及精度估算。总体蓄积量估计值为

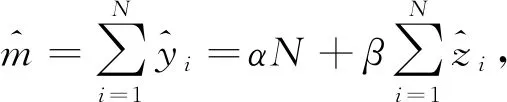
(23)

(24)

估计值的误差限和估计精度与两重回归相同。

3.3 估测结果

依据前面的估测方法，以人工修正乔木林蓄积为第一重样本、现地验证乔木林蓄积为第二重样本，采用双重回归估计方法对金寨等9县(市)LiDAR反演乔木林蓄积进行估测，获得总体及平原、丘陵、山区三个地貌类型的蓄积样本检验精度如表5所示(蓄积量估测值及估测区间因为数据成果的保密性，因此不便展示)。样本检验结果表明，LiDAR反演乔木林蓄积总体精度在90%以上，符合蓄积量产出精度要求。

表5 现地验证乔木林小班数统计表

4 结论

研究主要对森林蓄积量进行了基于激光雷达遥感数据的模型反演，依照评价体系选取了多元线性回归数学模型作为反演模型，采用随机分组10次10折交叉验证方法确定最优模型参数，反演模型的拟合能力较强，模型精度也较好。针对实际生产应用中，常运用人工验证结果来反映反演精度，研究采用了两步回归估计方法，既兼顾了激光雷达数据信息反演的结果，又结合了人工修正和现地验证数据的结果，得到了整个反演方法的精度估算，结果也十分良好。