关于McKay箭图的一点注记
侯汝臣
(烟台大学数学与信息科学学院,山东 烟台 264005)
1 引言及准备工作
“表示理论是代数学中具有根本性的问题,是当前国际上数学研究的前沿重点课题,在数学的其他分支,量子物理学以及化学等其他学科中有深刻而广泛的应用”[1]。 “群对称是数学的灵魂,而研究群对称的基本工具是群表示论”[2]。 1980 年,MCKAY引入了McKay 箭图的概念[3],它揭示了有限单群的表示和李代数、Klein 奇点等数学领域的联系,这就是经典的McKay 对应[4]。 在代数表示论中,McKay 箭图在研究 Cohen Macaulay 模的 Auslander Reiten 箭图,温驯型遗传代数的预投射代数,箭图簇,以及复杂度为2的自内射Koszul代数等多个方面起到重要作用[5-12]。
设G⊂GL(m,)=GL(V)是一个有限子群,这里V表示上的一个m维向量空间。 设 {Si|i=1,2,…,n}是G在上不可约表示的完全集。 对每一Si,将G的张量积表示V⊗Si分解为G的不可约表示的直和:群G的McKay 箭图Q=Q(G) 定义为:顶点集Q0是G在上不可约表示同构类下标的集合,从顶点i到顶点j有ai,j条箭向。 特别地,顶点i到i的箭向称为环。
一般情况下,计算McKay箭图比较困难[13]。 郭晋云利用代数表示论中的方法,即在文献[14]中利用文献[15]中外代数的斜群代数的箭图即为群的McKay箭图的方法,对有限循环群的McKay箭图进行了一般概括性刻画。 而因为有限循环群
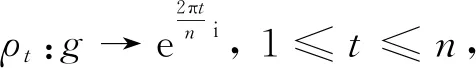
证明因为
设(ρ1,), (ρ2,) 为

设G是一个n阶有限循环子群。 易知,在单同态意义下,G总可以看做一般线性群GL(m,) 的子群,m∈+。 而在相似等价意义下,G在GL(m,)中的矩阵表现形式有哪些,是一个值得研究的问题。 引理2对此进行了刻画。
引理2在相似等价意义下,
其中ωi(i=1,…,m)是n次单位根,并且ωi的阶数的最小公倍数是n。
证明根据文献[16]中14节命题(4)(i),g可以相似对角化,再由引理1,g的特征值为n次单位根,所以存在群同态φ:
其中ωi(i=1,…,m)是n次单位根。 若要此同态为单同态,必须

且对任意p∈, 0 这就等价于要求n次单位根ωi(i=1,…,m)的阶数的最小公倍数为n。 依据GL(m,)对m矩阵乘法作用,m自然成为群G-表示。根据Maschke定理,群G-表示m可以分解为群G的不可约表示Si的直和,i=1,2,…,n。 但G在GL(m,)中的矩阵表现形式不同,所得到的m的不可约表示Si的直和分解也会不同。 下面定理1对此种现象进行了刻画。 在此基础上,自然地,在Grothedieck群意义下,以Si为基底,我们就可以得到群G-表示m的维数向量。 此向量在利用群的特征标求群的McKay箭图时也会起到重要作用。 我们回忆一下,设V是一个群G-表示,则V的维数向量定义为:dim(V)=(k1,k2,…,kn)T。 定理1设 (1)此时的群 (2) 群 证明根据引理2,在相似等价意义下, 设n阶循环群 其中ωu(u=1,2,…,m) 为n次单位根,并且ωu(u=1,…,m)的阶数的最小公倍数为n。 设j∈{1,2,…,n},则由引理1, 欲求群 即 例1设 则此时dim(4)=(0,2,2,0,0,0)T。 若 则此时dim(4)=(1,1,0,1,0,1)T。 定理2设 推论1n阶循环群 证明任取 由定理2,在不同单同态下, 推论2设 证明根据McKay箭图的定义,显然 现在就文献[15]中例4.3中的3个例子对定理2的应用加以说明。 例2设 则此时dim(3)=(2,1)T,3≅2S1⊕S2。 我们有a1,1=d2=1,a1,2=d1=2,a2,1=d1=2,a2,2=d2=1。 McKay箭图见图1(a)。 若 则此时dim(3)=(3,0)T,3≅3S1。 我们有a1,1=d2=0,a1,2=d1=3,a2,1=d1=3,a2,2=d2=0。 McKay箭图见图1(b)。 若 则此时dim(3)=(1,2)T,3≅S1⊕ 2S2。 我们有a1,1=d2=2,a1,2=d1=1,a2,1=d1=1,a2,2=d2=2。 McKay箭图见图1(c)。 图1 McKay箭图 通过和文献[15]比较我们不难发现,通过定理2的方法计算有限循环群的McKay箭图更简单。
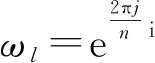
2 有限循环群的McKay箭图







