铰支多跨梁变形计算的正弦级数法

史文谱,闫家正,王 浩

(烟台大学机电汽车工程学院,山东 烟台 264005)

多跨梁在桥梁建设、海港码头和船舶工程中是十分常见的结构,其受载是比较复杂的,多数设计需要有限元等数值计算方法才能完成,但理论方法研究也一直是人们关注的热点。比如文献[1]中介绍的力法和三弯矩法是典型的解除约束法,它们的特点是需要事先解除约束,写出(分段)弯矩函数,利用变形协调条件列出补充方程,对于受载个数多的场合,还要考虑采用叠加原理分别求解,过程较繁琐;王秀华等[2]提出的积分法是在梁截面弯矩函数中预先考虑了待定约束反力,然后直接积分挠度-弯矩近似微分方程,并利用定解条件确定积分常数和多余约束力;朱伊德在文献[3]中提出的预先把挠度假设为一个有限项幂级数的方法,是利用了挠度、转角、弯矩、剪力和载荷集度之间的微分关系,借助问题的定解条件确定未知系数;文献[4]中韩晓娟给出的方法是在三弯矩法基础上引入刚度系数和载荷分布系数,在一定程度上简化了连续静不定梁变形的计算过程;此外,还有奇异函数与拉普拉斯变换相结合的方法[5-6]、有限元分析法[7]、传递矩阵法[8]和沃尔特拉积分方程法[9]等;熊剑峰等[10]利用傅里叶级数展开、哈密顿原理和伽辽金方法，研究了任意边界条件下多跨梁在轮印载荷作用下的位移响应解;李银山等[11]对多跨梁影响线问题提出了一种连续分段独立一体化的积分法,能够做到快速解析求解;贺坤龙等[12]利用ANSYS软件对三跨波形钢腹板连续梁弯桥分别承受集中载荷和连续分布载荷作用,在四种不同支撑条件下的剪力滞效应问题。不同于上述方法,本文针对两端铰支多跨连续梁变形计算问题提出的正弦级数法,是预先将挠度假设为自动满足连续梁两端挠度和弯矩为零条件的正弦级数,利用梁中间支撑处挠度为零的边界条件和最小势能原理,推出级数中未知系数满足的无穷线性代数方程组,然后在满足计算精度基础上进行有限项截断求解。该方法无须解除约束,无须列出弯矩函数,无须利用叠加原理单独考虑每种载荷产生的变形,故计算过程和步骤简单方便,计算精度高,给出的数值算例结果说明了方法的可行性。

1 理论模型与分析

图1 多跨梁受力分析

考虑到文中讨论的多跨连续梁的两端是铰支的,故其挠度和端部弯矩始终为零。因此，无论梁承受什么样的载荷作用,可以将梁的挠度函数w(x)在区间[0,L]内的曲线周期性延拓展开为无穷区间(-∞,∞)上的正弦级数(周期为2L)，如式(1):

(1)

其中:ak(k=1,2,…,∞)是待定系数。

根据图1,式(1)还应满足如下方程组

w(Lj)=0,j=1,2,…,n-1,

(2)

即

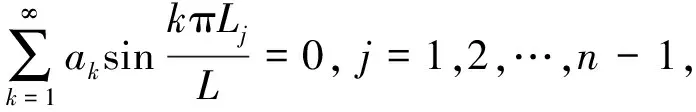
(3)

由方程组(3),理论上总是可以解出n-1个未知量,比如a1,a2,…,an-1,它们均可以由剩余的待定系数an,an+1,…线性表示出来,假设取如下形式:

(4)

其中:βkt(k=1,2,…,n-1;t=n,n+1,…)是表达式系数,它们可由下列线性代数方程组确定,即

j=1,2,…,n-1;t=n,n+1,…,

(5)

其对应的矩阵表示形式为

(6)

多跨连续梁静力平衡后,系统的总势能U(a1,a2,…,an)可表示为

U(a1,…,an)=

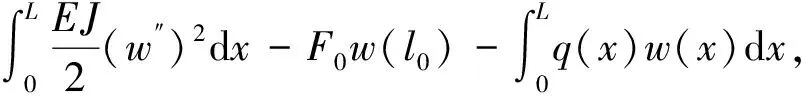
(7)

其中:w″(x)是挠度函数w(x)关于x的二阶导数,w(l0)是挠度函数在l0处的值,它们分别可表示为

将式(4)代入式(7)中,系统的总势能函数U(a1,a2,…,an)应为待定系数(an,an+1,…)的二次函数。

根据最小势能原理有

(8)

即

(9)

其中:t=n,n+1,…。

将式(1)代入式(9)中整理得

通过上述方程(5)或(6)(利用计算机可轻松完成)预先可以求得一系列βkt(k=1,2,…,n-1;t=n,n+1,…),然后利用式(10),求得aj(j=n,n+1,…),进一步利用式(4),求出ak(k=1,2,…,n-1),最后通过式(1)确定多跨梁的挠度函数w(x)。

为了比较和验证本文方法的计算效果,把材料力学中解除约束法给出的挠度函数假设为w1(x),则绝对计算偏差δ(x)定义为

δ(x)=|w(x)-w1(x)|,x∈[0,L]。

(11)

2 数值算例及分析

算例1以一个双跨连续梁承受其自重和集中力F0的作用问题为例(图1),其中F0=300 N,l0=2.0 m,L1=3.0 m,L=4 m;E=2.5×109N/m2,梁采用矩形方管制作,截面外部宽度和高度分别为b=0.2 m和h=0.4 m,内部宽度和高度分别为b1=0.19 m,h1=0.39 m,梁的重力线密度为q=465 N/m,方向向下,按照本文方法(实线)和解除约束法[1](虚线)分别计算,结果如图2(2种方法计算结果完全重合,无法分辨)。为了看出两者之间的细微差别,可参看绝对计算偏差δ(x)的变化曲线(图3)。从图3看,两者的绝对偏差在中间支撑处有较为剧烈的波动变化,在集中力F0作用处附近也有小许波动,但变化幅度最大值都不超过1.751 3×10-12m,在双跨梁的整个长度范围内,计算偏差δ(x)∈[0,1.751 3×10-12]m,完全可以忽略。

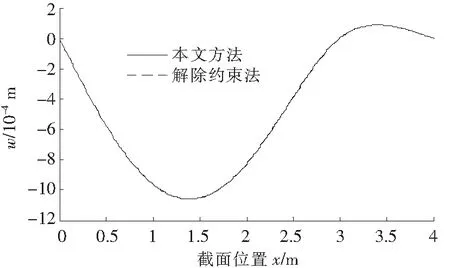
图2 双跨梁挠度变化曲线

图3 双跨梁挠度计算偏差变化曲线

Fig.3 Calculation deviation curve of deflection of double-span bean

这里,计算精度取为ε=10-5,无穷线性代数方程组(10)中取用100个方程,即挠度的正弦级数中取用了前N(N=101)项。从图2还可看出,本文计算的挠度曲线在点x=0,3,4 m处取值为零,完全满足问题的边界条件。按照文献[1]推出的解除约束法的挠度函数表达式w1(x)较为繁琐,这里略去不写。

算例2三跨连续梁承受集中力F0和自重q的作用(图1),其中F0=300 N,梁采用矩形方管制作,截面外部宽度和高度分别为b=0.2 m和h=0.4 m,内部宽度和高度分别为b1=0.19 m,h1=0.39 m,(方管)自重线密度q=463.15 N/m。其他已知参数L0=3.0 m,l1=2.5 m,l2=3.0 m,l3=3.5 m,L=9 m，E=2.5×109N/m2，L1=l1=2.5 m,L2=l1+l2=5.5 m,L=9 m。计算精度取为ε=10-5,对上述无穷方程组(10)取用100个方程,即挠度的正弦级数中取用了前N(N=101)项,结果如图4(实线)。同时在该图中也绘出了解除约束法[1]的结果(虚线),两者是重合的,两者的计算偏差曲线如图5,计算偏差在梁的总跨度范围内的变化区间是[0,3.480 8×10-10]m。从图5看,计算偏差在x=2.5 m和x=5.5 m这2个中间支撑处附近波动变化较为强烈,在集中力F0作用点x=3 m处附近也有不太明显的小幅波动,但无论怎样,它们的波动幅度都未超过3.480 8×10-10m。

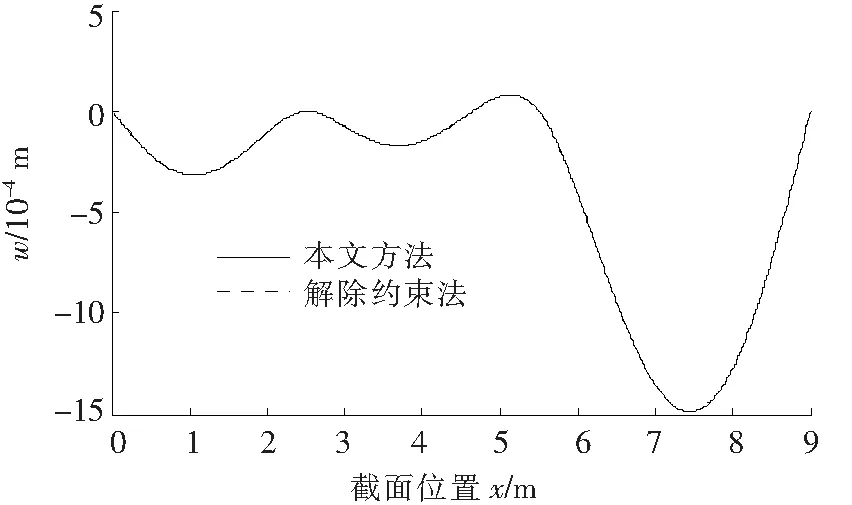
图4 三跨梁挠度变化曲线

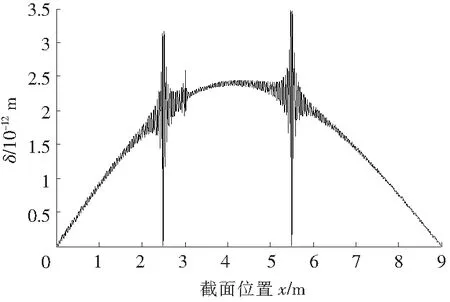
图5 三跨梁挠度计算偏差变化曲线

Fig.5 Calculation deviation curve of deflection of three-span bean

3 结束语

针对两端铰支多跨梁的挠度计算问题,提出了利用最小势能原理的正弦级数解法,该法具有如下几个特点:

(1)无须解除约束,无须列出弯矩函数,无须计算复杂的莫尔积分或分段常微分方程组定解问题;

(2)2个算例的计算结果表明,只要在挠度的无穷正弦级数中选用前100项即可保证较高的计算精度,且与材料力学[1]的解除约束法的结果在计算精度范围内完全一致;

(3)对于多个载荷作用的情形,无须利用叠加原理分别求解结果再求和,而是统一一次性处理,因而计算效率较高。