Sigma-Delta模数转换器的三级数字抽取滤波器设计
胥珂铭,高 博,龚 敏
(四川大学物理学院,成都 610065)
1 引言
高分辨率的数据成为了现代生物医学信号处理系统中的重要参数之一[1-4],SAR ADC在这种使用环境下精度不足以满足要求[5]。Sigma-Delta ADC是最合适的高分辨率结构,而且容易集成到信号处理系统中[6]。Sigma-Delta ADC结构分为调制器和抽取滤波器两个主要部分,目前调制器的设计可以达到120 dB以上[7-9],这对抽取滤波器的设计提出了高性能要求。在Sigma-Delta ADC中,抽取滤波器是功耗最大、占面积最大的模块。单极滤波器难以在高阻带抑制、平坦的通带、降采样上达到设计目标[10-11]。一些文章采用多级滤波器结构,其中第一级常为CIC滤波器加补偿滤波器进行降采样[12-14]。CIC滤波器无乘法器,用于降采样可以有效降低滤波器面积,但是其有明显的带内衰减,需要加入有乘法器的补偿滤波器设计,又增加了部分面积[15];有文章把CIC滤波器的补偿滤波器当作第二级,即CIC滤波器、FIR补偿滤波器、半带或FIR滤波器的三级结构,这种结构相比第一级为CIC滤波器加补偿FIR滤波器的结构来说,面积更小,但是阻带抑制不如之前的结构[16];也有文章在设计中把FIR滤波器替换成无限脉冲响应数字滤波器(Infinite Impulse Response Filter,IIR Filter),相比FIR滤波器,IIR滤波器计算更简单,面积相对较小,但IIR滤波器有非线性相位的问题,需要额外增加相位补偿器,或用于对相位不敏感的系统中[17]。锐化CIC滤波器对通带宽度和阻带抑制都有改善[18],但是对面积和功耗都有一定的妥协。
本文提出一种低面积、高精度的抽取滤波器结构,滤波器的降采样率为32。该滤波器级联了4阶4抽SCIC滤波器,29阶4抽FIR滤波器和148阶2抽的半带滤波器。其中SCIC滤波器有良好的通带带宽和混叠带抑制且不需要补偿滤波器,后两级滤波器使用乘法器复用级数,极大压缩乘法器数量,在不影响性能的情况下减少逻辑单元数量,降低FPGA资源消耗。
2 多级级联滤波器
该滤波器的降采样率为32,预设滤波器采样频率为20 MHz,第一级SCIC滤波器设计为最大平坦通带,后两级FIR滤波器工作在更低的频率,且使用了很少的乘法器,以降低资源消耗。整体系统结构如图1所示,图中L为滤波器阶数,x(n)为SCIC滤波器输入,y(n)为SCIC输出。第一级SCIC滤波器采用了递归结构,第二级为一个尽可能少系数的FIR滤波器。第一级与第二级的主要作用是降采样,同时防止信号混叠,其中第一级SCIC滤波器是主要的混叠可能产生的结构。第三级则是一个半带滤波器,因为半带滤波器有一半的滤波器系数为0,且其通带总是在奈奎斯特频率的一半处。半带滤波器没有通带波纹,在第一级与第二级的降采样下,乘法器复用数量可以更大,更加节省FPGA资源,这一级在降采样的同时对阻带进行有效的抑制。

图1 多级级联滤波器整体结构
2.1 第一级
第一级为一个SCIC滤波器,该滤波器结构由KWENTUS等人提出[19],传递函数的z域表达式如下:
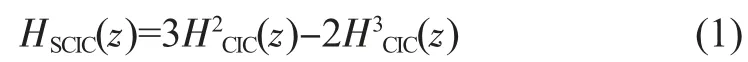
其中传递函数HCIC(z)为

M为抽取率。
多阶SCIC与4阶CIC滤波器对比的频率响应如图2所示,图2中纵坐标为阻带衰减,横轴为归一化频率。4阶SCIC滤波器与4阶CIC滤波器相比,其通带更宽,阻带抑制也更高。SCIC滤波器级数的旁瓣衰减比CIC滤波器更大,每多一级旁瓣衰减增加约22 dB。级数同样影响混叠带抑制,在固定4抽取的情况下,3阶4抽SCIC旁瓣衰减有58 dB,混叠带抑制有135 dB,而4阶4抽SCIC旁瓣衰减有80 dB,混叠带抑制有180 dB,虽然5阶4抽的SCIC滤波器旁瓣衰减有100 dB,且阻带抑制超过200 dB,但对于本滤波器设计,第一级滤波器的降采样和防混叠目标只需要4阶4抽SCIC就可以满足,没有继续提高阶数的需求。所以应用在本次设计中,设计为4阶4抽SCIC,其通带可以满足滤波器系统通带290 kHz,在通带处的衰减仅为0.011 dB,因此完全可以省去补偿滤波器,同样条件下CIC滤波器通带有0.18 dB的衰减,需要添加补偿滤波器。虽然SCIC滤波器需要复数个CIC滤波器,但是省略了补偿滤波器的结构,FIR补偿滤波器存在大量加法器与乘法器,因此减少补偿滤波器后整体的资源消耗是降低的。4阶4抽的SCIC滤波器混叠抑制超过150 dB,通带衰减小,可以达到设计目标。
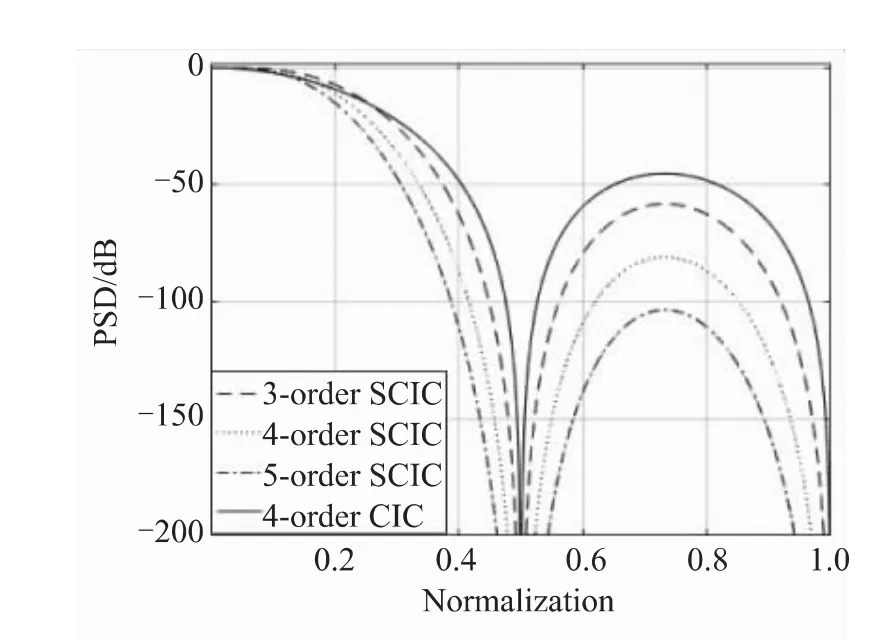
图2 SCIC频率响应
该SCIC滤波器是非递归结构[19],相比递归结构,非递归结构的所有模块都需要全字长,且因为SCIC结构是3个CIC滤波器级联,因此每增加一位输入位宽,相对于CIC滤波器需要增加3倍的寄存器,这对于节省资源是不利的。为了节省资源,本设计中把SCIC修改为递归结构。对于式(2)中(1-z-M)可以拆分为

其中(1-z-1)可与式(2)分母约分,得到:
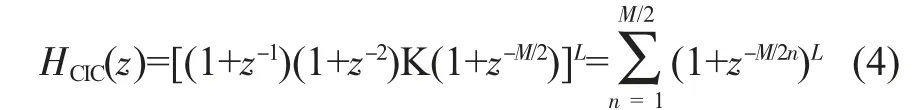
根据第一稀有恒等式,对于(1+z-M/2n),如果经过M/2n抽取率会变为(1+z-1),因此把CIC滤波器结构改变为多个(1+z-1)级联,每个级联之间加入2抽取,CIC结构只有(1+z-1)的模块。这就是递归结构的CIC滤波器。递归CIC滤波器每个(1+z-1)模块固定增加一位字长,不需要所有模块增加全字长,因此节省了寄存器,相比非递归结构达到了节省资源的作用。
对于SCIC,其为3个CIC滤波器级联,把CIC滤波器改为递归结构后,其递归结构如图1所示,其传输函数如式(1)所示。
2.2 第二级
第二级为一个29阶4抽的FIR滤波器,FIR滤波器传递函数如下:
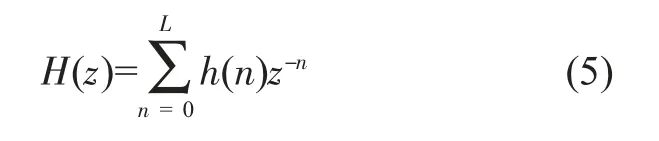
其中h(n)为滤波器系数。
该级FIR滤波器主要作用是降采样,因此对于过渡带不做过多要求,设计主要目标在阶数、通带波纹和阻带抑制平衡。其中最重要的是通带波纹,高精度的滤波器需要通带足够平坦,因此不能有太大的通带波纹,这一级的通带波纹设计为0.01 dB。FIR滤波器的阻带抑制不需要太大,设计为60 dB防止混叠,在满足这两个要求的情况下,设计阶数为29阶,使用乘法器复用结构后正好只需要一个乘法器即可以完成29阶系数的计算,对于乘法器的节省有很好的作用。乘法器复用结构将在下面介绍。最终FIR滤波器参数如表1所示。

表1 第二级参数
为了节省资源,FIR滤波器与下一级半带滤波器均采用了乘法器复用结构,其结构示意图见图3,图中datain为输入信号,coefficient为FIR滤波器参数。乘法器复用包含乘法器部分和累加器部分。对一个复用的乘法器,在每个主时钟同步更换系数和输入进行乘法计算,最后再把整组的输出数据累加得到结果,如果一个滤波器结构中使用到了多个乘法器,只需要在输出时把多个累加器输出相加即可得到输出信号。这种结构下,一个乘法器能计算的系数由分频时钟与主时钟的倍差决定,本设计中,滤波器处的分频时钟是主时钟的1/4,因此一个乘法器可以计算4个系数,又因FIR滤波器的系数是对称的,所以一个乘法器可以支持9阶FIR滤波器的计算。更进一步,因为FIR滤波器的抽取是对完成计算的输出进行抽取,而未被抽取的输出则被浪费了。因此对于FIR滤波器,使用一组寄存器保存输入,且在只抽取后更新数据,乘法器的输入信号变为该组寄存器,则乘法器复用可以用一个乘法器计算(主频时钟/分频时钟×本级抽取率)个系数。如第二级设计中,一个乘法器可以计算16个系数,而29阶FIR滤波器存在15个不同的系数,则该FIR滤波器只需要一个乘法器即可完成计算。乘法器复用结构可以有效减少乘法器数量,但是会增加寄存器数量,因此需要考虑为了减少乘法器而增加寄存器是否划算。

图3 乘法器复用结构
2.3 第三级
第三级为一个148阶2抽的半带滤波器,半带滤波器是一种特殊的FIR滤波器,其传递函数与式(3)相同,半带滤波器的特点是偶数次系数全为0,奇数次系数不为0,其中不为0的系数与FIR滤波器一样是对称的。因此半带滤波器的系数实际上只有阶数的1/4,且半带滤波器的通带一定在归一化频率的1/2左右。
半带滤波器通带波纹很小,因此主要考虑过渡带带宽和阻带抑制。第三级是最后一级,为了防止混入噪声,所以阻带抑制应该足够高,而且过渡带不应过大,根据乘法器复用结构,第三级的主频时钟和分频时钟差距更大,因此一个乘法器可以计算更多的系数,在这样的条件下,可以适当放宽阶数,主要达到过渡带和阻带的要求。在这样的设计目标下,该半带滤波器有120 dB的阻带抑制,过渡带为62.5 kHz,其设计参数如表2所示。对于该滤波器,同样使用乘法器复用结构,根据之前的计算,148阶半带滤波器有74个系数,38个不重复系数。考虑到最后一级如果使用寄存器在抽取后更新输入以节省乘法器的设计方法,会增加(148×24)位寄存器,而只能节省一个乘法器,寄存器面积增加太大而不划算。因此使用3个乘法器是更节省面积的办法,相比正常的38个乘法器有效节省了逻辑单元。

表2 第三级半带滤波器参数
3 仿真结果
三级滤波器级联频谱响应如图4所示,图中纵轴为阻带衰减,横轴为频率。从图4可以看到,级联滤波器通带内很平整,其中第一级与第二级滤波器主要用于降采样,同时防止奈奎斯特频率内出现信号混叠。前两级的过渡带宽度都大于第三级的奈奎斯特频率,因此,阻带抑制主要依靠第三级滤波器的设计。第三级半带滤波器有120 dB的阻带抑制,且其过渡带很小,可以有效防止混入噪声。

图4 三级滤波器级联频谱响应
滤波器使用Verilog HDL代码进行实现,使用Quartus软件进行综合,综合结果如表3所示。对滤波器代码进行前仿,使用MATLAB的Simulink设计的五阶反馈调制器输出作为滤波器信号输入,该调制器输出250 kHz理想信号的SNR为149 dB,调制器输出频谱信号如图5所示。把Verilog HDL代码下载到Altera DE10 FPGA开发板,使用DE10开发板HPS端的网线把经过滤波器结构处理后的数据传输到电脑,使用输出的数据进行SNR计算,得到SNR结果为134.6 dB,有效字长(Enable of Bits Number,ENOB)为22位,仿真SNR计算结果如图6所示。图6存在一个直流分量,而图5不存在,这是因为图5使用Simsides进行频谱绘制,而图6使用MATLAB的SNR函数进行绘制。

图6 仿真SNR计算结果

表3 Quartus软件综合结果

图5 调制器输出信号频谱
对比图5和图6可以发现,图5调制器输出的信号在通带内随着频率增大而增大,而图6中滤波器输出信号的通带内频谱是基本平坦的。造成这样的原因在于实际设计滤波器时,为了平衡硬件消耗和性能,对通过滤波器的信号进行了截取。本文中,输入的调制器信号为15位位宽,每级滤波器输出都截取高24位信号,这样做会导致低频的噪声被拉高,表现出如图6一般的平坦通带。截取位宽选择24位是因为根据调制器SNR推算,最终输出有效位宽在24.5位以内,因此选择最终输出24位信号,最后计算ENOB达到了22位,效果较好。截取信号可以节省大量的寄存器,比如在本文中,后两级滤波器的参数量化为24位,和24位信号卷积后,输出信号超过50位宽,这时进行截取,则可以节省一半寄存器。位宽截取对SNR的影响较小,在实际设计中对输出信号进行截取是有必要的。
为对比本文设计节省的FPGA资源,在表3中加入了一个未使用SCIC滤波器与乘法器复用结构的对照组。该对照组由CIC滤波器、补偿FIR滤波器、FIR滤波器和半带滤波器组成,其中CIC滤波器结构为4阶4抽;补偿FIR滤波器为新设计的20阶、通带波纹0.01 dB、阻带抑制20 dB的FIR滤波器;后两级FIR滤波器与半带滤波器参数未作改变,但并没有使用乘法器复用。最终该设计综合后占用FPGA如表3中对照设计所示,可以看到不管是逻辑单元数量还是寄存器数量相比本文设计都有了较大的增加,其中本文设计的逻辑单元比对照组节省了26.3%,而寄存器节省了15.6%。
4 总结
本文提出了一种适用于Sigma Delta ADC抽取滤波器的高分辨率、低面积的三级滤波器结构,该滤波器在高精度的前提下,节省了大量FPGA资源。设计主要在第一级节省了补偿滤波器和FIR滤波器的乘法器复用结构,这两者都减少了乘法器的数量,大大减少了滤波器逻辑单元的消耗;乘法器复用结构同样节省了大量的寄存器,因此本文的设计节省了逻辑单元和寄存器。
在使用5阶调制器的理想输出对滤波器进行仿真的情况下,滤波器输出的有效位宽达到22位,使用Quartus进行板级综合,相比普通设计节省了26.3%的逻辑单元和15.6%的寄存器,其结果符合高精度、低资源消耗的设计目标。
本设计已通过FPGA板级验证,对于乘法器复用和SCIC滤波器可节省补偿滤波器结构,在门级综合里也可大量节省面积,设计出低面积、高精度的抽取滤波器结构。

