Aigis密钥封装算法多平台高效实现与优化
沈诗羽 何 峰 赵运磊
(复旦大学计算机科学技术学院 上海 200433)
近年来,为应对大数据和互联网时代对计算能力的需求,各国都对量子计算研究投入了极大的力度和资源.谷歌、IBM、阿里、腾讯等公司相继成立了实验室来研究量子计算与后量子安全技术.谷歌于2019年研制出53位量子比特计算机[1], 可于3 min 20 s内完成世界第一超级计算机Summit一万年才能完成的计算任务.2020年Yang等人[2]研制出能在超过1 K温度下运作的量子计算平台,在实用性方面取得了巨大的突破.2021年美国芝加哥大学和阿贡实验室研究人员利用超导同轴电缆提高量子态传输保真度,首次实现确定性多量子比特纠缠,为构建大规模量子计算机提供了一种模块化的方法[3].
量子计算主要通过利用量子叠加与纠缠两大量子物理学特性带来的强大并行处理性来超越经典计算的性能,且其计算模型中的特殊性质也给抗量子密码算法方案设计带来了巨大挑战.随着量子计算机的出现与量子计算技术的不断推进,现代密码算法面临着前所未有的挑战.传统的公钥密码设施大多基于离散对数或大整数分解困难问题,如联邦信息处理标准出版物(FIPS)186[4]中规定的数字签名方案和美国国家标准与技术局(NIST)特别出版物(SP)800-56A和(SP)800-56B[5-6]中规定的密钥建立机制. 这些公钥密码算法虽然目前尚无法被传统计算机攻破,但是均可在量子计算机中找到多项式时间的破解方法[7]. 密码技术是国家网络空间安全的关键技术,公钥密码体制在网络、金融、军事等方面都有着举足轻重的作用,它被广泛用于各种网络安全协议中,如IPSEC,TLS等.因此,实现抵抗量子攻击的新型密码体制,即后量子密码(post-quantum cryptography, PQC),是目前重要的研究方向.
为了应对量子计算的威胁,2016年美国国家标准与技术局(NIST)开展后量子密码算法征集,向全球学者征集后量子密码算法[8].2019年中国密码学会也举办了全国密码算法设计竞赛,旨在为我国制定后量子算法标准做准备[9].后量子密码的构造主要包括基于编码(Code-based)、基于哈希(Hash-based)、基于多变量(Multivariate-based)、基于格(Lattice-based)和基于同源(Isogeny-based)的.近期, NIST宣布了第3轮7个进入决赛(finalists)的算法[10],其中5个是基于格构建的. 相较于其他后量子密码技术路线,基于格的密码方案具有理论上的最坏情况困难保证[11],计算速度更快,更易于并行,而且通信开销较小,可用于构造多种功能强大的密码方案,如公钥加密、数字签名、全同态加密等.我国密码算法设计竞赛一等奖Aigis方案[12-13]即是格上构建的基于非对称模-LWE(A-MLWE)与非对称SIS(A-SIS)困难问题的方案,包含密钥封装机制Aigis-enc与数字签名方案Aigis-sig. 对于密钥封装机制,相比于NIST第3轮中基于MLWE问题的Kyber方案,Aigis密钥封装算法(简记为Aigis-enc)需要基于额外的假设,但通过压缩公钥以及密钥和噪声从不同的分布中采样,Aigis-enc在安全性与错误率之间取得了更好的权衡.
为了应对量子攻击,维护国家网络空间的长远安全,为未来国家后量子密码算法标准的制定和实际部署贡献力量,对我国自行研发的优秀后量子密码算法进行优化具有重要意义.本文重点关注Aigis-enc算法在不同平台的实现优化,包含高性能平台的快速并行实现与嵌入式低功耗平台的紧凑实现.对此,本文充分利用了单指令多数据(single instruction multiple data, SIMD)指令集,如Intel的AVX2指令集和ARM Cortex-M4的数字信号处理(DSP)指令集, 对算法底层多项式运算以及算法运行所需堆栈与存储空间进行优化. 特别地,据我们所知,本文工作提供了首个Aigis-enc的ARM Cortex-M4平台的轻量级紧凑实现. 具体而言,本文的主要贡献有5个方面:
1) 使用了改进版有符号数Montgomery约减与Barrett约减,并运用乘加指令减少了ARM Cortex-M4平台模约减所需指令条数,提升约减效率;
2) 使用了删减层数的数论变换(T-NTT)并提供AVX2与ARM的汇编实现,相比与传统NTT,删减了变换的最后一层,极大地减少了预计算表存储需求;
3) 对多项式压缩并编码为字节流和字节流解码并解压缩这2个核心多项式序列化与反序列化操作,使用一个乘法和一个移位运算来替换耗时高的除法,并借助AVX2并行处理加快整个过程;
4) 调整算式结构以充分适应各平台指令特性,从而达到减少总指令数目与load/store指令开销的目的;
5) 采用on-the-fly计算与空间复用的优化方法,大幅减少了运行所需堆栈空间、代码大小以及存储占用.
实验结果表明:综合本文提及的优化技术,在8核Intel Core i7处理器上可将Aigis-enc算法原始AVX2实现提升25%,且大幅减少了其在ARM Cortex-M4平台的预计算表存储、代码尺寸与运行堆栈占用,对算法实际应用有重要价值.
1 相关工作
基于格的密码体制首先由Ajtai[14]提出.2005年Regev[15]提出的格上基于错误学习(LWE)问题的密码方案极大提升了格密码算法的效率,目前格密码已经成为密码学领域的研究热点.NIST后量子标准化进程中,基于模格的密钥封装算法Kyber是第3轮入选算法之一.Zhang等人[12]观察到MLWE问题的私钥与噪音分布对方案安全性与错误率的影响不对等,从而提出了A-MLWE与A-SIS问题,并在此基础上构造了Aigis算法.其中,密钥封装机制Aigis-enc可视为Kyber的变体,但能更好地平衡安全性与错误率.自第2轮算法提交以来,Kyber取消了对公钥的压缩,而Aigis-enc保留了该操作.
算法性能是衡量算法优劣的重要指标之一,近年来,学者们提出了很多针对格密码算法的软件优化实现方法[16],包含AVX2并行快速实现与ARM Cortex-M4平台的轻量级实现.2016年Alkim等人[17]公开了基于RLWE困难问题的NewHope算法,算法参数设计使得其适合使用数论变换(number theoretic transform, NTT)加速多项式乘法,且使用浮点型NTT进行实现.Avanzi等人[18-19]于2018年公开了Kyber第1轮算法实现,包含C参考实现、C优化实现与AVX2优化实现.该实现中使用了lbq层变换的整型NTT.随后,在第2轮提交中,该团队对算法参数进行了调整,删减了NTT层数以降低q的规模[20].对于ARM Cortex-M4平台实现,pqm4[21]提供了一个Cortex-M4微处理器上算法运行时钟周期与堆栈空间的测试框架.目前,Kyber算法的M4实现已被纳入该项目.2020年Alkim等人[22]基于其2016年的工作[17],对NewHope算法的设计与ARM实现进行改进,并使用该技术优化了Kyber的堆栈使用.
目前尚未有针对7681模数的汇编指令实现.本文在充分结合运用这些优化技术的基础上,进一步调整代码运算结构,优化了多项式序列化、加解密过程,结合空间复用等方法,将指令个数与存储降至最低,从而给出了首个针对该模数高效紧凑的优化实现方案.
2 预备知识
本节给出了本文工作相关的预备知识.首先定义了变量符号、数学运算与格上困难问题,接着详细描述Aigis-enc算法并介绍了实现平台与优化方式.
2.1 基本定义及符号说明
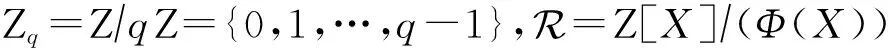
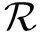
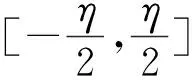
4) 算法参数.算法方案描述中,n为多项式的维度,q为模数,l表示向量的维度,lbm表示消息编码中1 b可编码结果的个数.此外,η表示噪声的大小,d(或t)表示Zq域的整数被压缩(或删减)的比特数,g=2d,其下标指示操作对象.pk,sk与ct分别表示公钥、私钥与密文,B为通信带宽,是公钥和密文长度的总和(单位为字节).方案分析中,δ表示解密的错误率,pq-sec表示后量子安全等级,K表示待封装密钥.
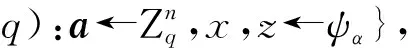
2.2 Aigis-enc算法介绍
Aigis-enc方案是基于A-MLWE困难问题的后量子密钥分装算法,其核心构造为IND-CPA安全的公钥加密PKE=(KeyGen,Enc,Dec),由密钥生成、加密和解密3个部分组成,遵循文献[23]的设计框架.在此框架基础上,通过FO转换(Fujisaki-Okamoto transformation)[24]可构建IND-CCA安全的密钥封装机制KEM=(KeyGen,Encaps,Decaps).由于目前FO转换已有较为统一的模块化实现方案,且多为对PKE所涵盖函数接口的调用,所以本文重点关注Aigis-enc方案中IND-CPA安全的公钥加密模块,进而开展对底层多项式运算的优化实现.在文献[23]加密框架的基础上,私钥与噪音服从中心二项分布χα,其值在区间[-α,α]内.Zhang等人[12]观察到,α的值对方案安全性与正确性起着不对等的作用,换模压缩技术的使用也使得秘密向量及其对应的噪音向量在最终噪音项中起着不对等的作用.由此,Aigis-enc中秘密向量与噪音向量分别从不同的分布χs与χe中采样,选取了非对称体制来平衡参数间的影响.
Aigis-enc-PKE的密钥生成算法如算法1所示.密钥生成时首先从n位二进制串中均匀采样出σ和ρ,然后将随机种子ρ传入Sam和Parse函数以生成NTT域上的矩阵A,接着以σ为参数通过CBD算法生成私钥s和噪音向量e,最后计算As+e后并压缩,与ρ拼接形成公钥pk.
算法1.Aigis-enc-PKE密钥生成算法.
输出: 公钥pk(t,ρ),私钥sks.
① functionAigis-enc.KeyGen( )
②σ,ρ←{0,1}n;
③A~Parse(Sam(ρ));
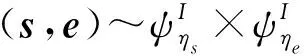
⑤tCompressq(As+e,dt);
⑥ return (pk(t,ρ),sks).
⑦ end function
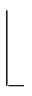
算法2.Aigis-enc-PKE加密算法.
输入:公钥pk(t,ρ)、待加密消息msg、随机数r;
输出:密文ct(c1,c2).
① functionAigis-enc.Enc(pk,msg,r)
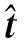
③A~Parse(Sam(ρ));
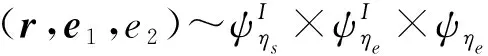
⑤uAT·r+e1;
⑥v
⑦vv+Decompressq(msg,dm);
⑧c1Compressq(u,du);
⑨c2Compressq(v,dv);
⑩ returnct(c1,c2).
Aigis-enc-PKE的解密算法如算法3所示.算法传入参数为密钥sk和密文ct,通过对密文ct,即c1和c2进行解压缩,分别得到u和v,最后解码v-sT·u得到明文msg.
算法3.Aigis-enc-PKE解密算法.
输入: 私钥sks、密文ct(c1,c2);
输出: 解密消息msg.
① functionAigis-enc.Dec( )
②uDecompressq(c1,du);
③vDecompressq(c2,dv);
④msgCompressq(v-sT·u,dm);
⑤ returnmsg.
⑥ end function
2.3 实现平台与SIMD指令
SIMD是一种采用一个控制器控制多个平行的处理单元、同时对一组向量化数据的每个元素执行相同操作的并行技术.相比于多进程并发运算,该技术实现的是空间上的数据级并行,同一时刻只有一个进程被执行.SIMD技术多用于实现一些简单的通用运算,如算术运算、逻辑运算、数据排列混合、数据批量加载与存储等.
高级向量扩展(advanced vector extensions, AVX)指令集是x86架构微处理器中一种128 b的SIMD指令集,由英特尔提出,随后也得到了AMD的支持.AVX2指令集是AVX的延伸,将大多数作用于整数上的指令扩展至256 b,以增加一倍的运算效率.另外,三操作数运算指令的支持也减少了操作数的额外复制消耗.
ARM Cortex-M4是ARMv7E-M架构的数字信号控制器,以满足高性能通用代码处理以及数字信号处理应用的需求.其核心通用指令集包含基本的Thumb-1,Thumb-2指令,以及32 b宽乘法.另外,ARM Cortex-M4也提供了SIMD指令,即数字信号处理(digital signal processing, DSP)扩展指令集.该指令集可在32 b宽的寄存器内同时对4个8 b或2个16 b整数进行操作.
在格密码算法中,底层操作多为互相独立的多项式系数算术运算与逻辑运算,非常适合用SIMD指令进行并行优化.Aigis-enc算法中多项式系数规模为16 b,使用AVX2可实现16个数据的并行运算,DSP可实现2个数据的并行运算,对多项式算数运算、模约减、数论变换等模块效率的提升有明显的效果.
3 Aigis-enc算法测试及优化函数选定
本节给出了gprof与nm工具下Aigis-enc-768实现的软件分析测试结果,并据此选定开销大、调用频率高或存储占用多的模块以进一步优化,如离散采样、多项式乘法、模约减等;对于尚未并行优化的函数,如多项式序列化与反序列化,本文也将其纳入优化范围.对于选定的函数,本节中给出了相关理论与算法描述.
3.1 Aigis-enc算法软件分析
Aigis-enc算法团队在中国密码学会官网上提交了Aigis-enc原始实现,作为第2轮算法竞赛的支撑材料[12].为确定实现中有待进一步优化的函数、从而提升算法整体运行效率与空间占用,本文使用gprof与nm工具对Aigis-enc-768算法实现进行了测试分析,结果如图1所示:
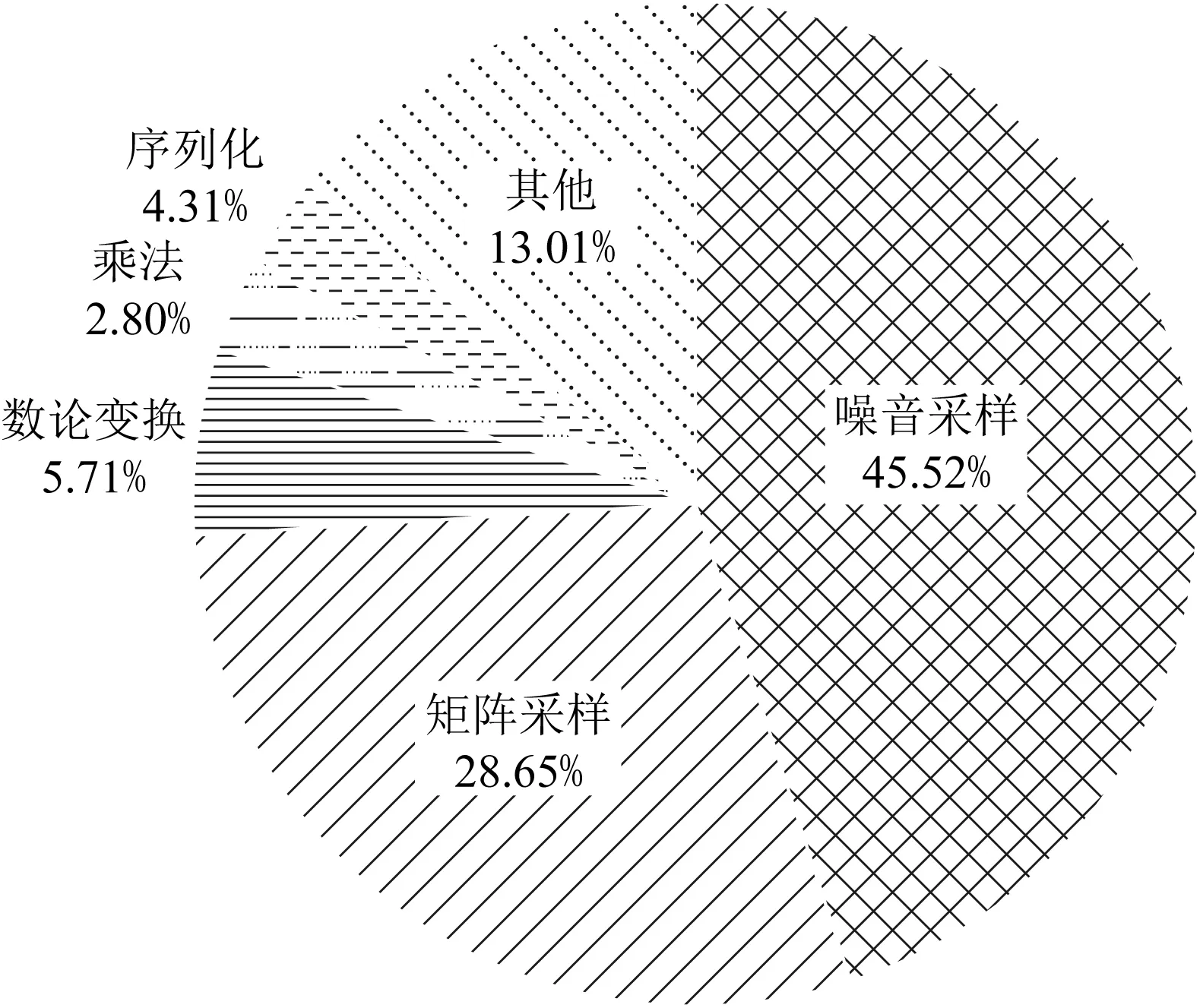
Fig. 1 Test results of the Aigis-enc-768 algorithm图1 Aigis-enc-768算法测试分析
结果显示,伪随机数扩展占用了61.70%的时间开销,主要用于噪音采样与矩阵A的生成,这2项运算所需时长分别为总体的45.52%与28.65%.一些多项式操作函数开销相比较大,如基于NTT的多项式乘法中,前向与逆向NTT共占5.71%,多项式向量的点乘占2.80%.此外,有4.31%的时间用于多项式序列化与反序列化,包含多项式压缩与解压缩、消息编码与解码等多项式与字节流间的转换操作,其中部分函数目前尚未进行并行优化.对于ARM平台的轻量级实现,内存与栈空间占用为算法优化的重要指标之一.nm工具得到的符号表显示,Aigis-enc-768代码大小为968.304 KB,其中,前向与逆向NTT分别占据了30 KB.另外,为控制数据规模,模约减函数在运算中调用频率较高.原始实现中模约减并无显式调用,而是实现在各个函数中,这也会造成代码冗余.
本文对Aigis-enc-768算法优化主要集中于多项式运算处理模块,对通用哈希模块暂不进行调整.对于结构复杂的函数,如NTT、模约减、压缩与序列化等,本文提供了汇编指令优化实现.结合工具分析结果,本文确定的主要优化点有2个方面:
1) AVX2.使用NTT变体提高多项式乘法计算效率;对未优化的多项式运算函数进行AVX2并行优化;提供部分函数的AVX2汇编指令实现,以优化流水调度;
2) ARM.减少NTT运算中预计算表大小;运用on-the-fly[22]等优化思想减少代码运行的栈空间;使用DSP指令减少运算所需时钟周期,并提升并行度.
3.2 模约减
多项式系数为群Zq中的元素,将其规约为群Zq中的代表元,可以控制系数规模,从而减小算法运行所需的时空资源.x86与ARM架构的处理器通常使用除法指令来完成取模运算.为此,密码算法实现中引入了Barrett约减与Montgomery约减,以减少除法运算带来的过多消耗,同时保证约减可以在常数时间内完成,以抵抗侧信道攻击.
3.2.1 Barrett约减
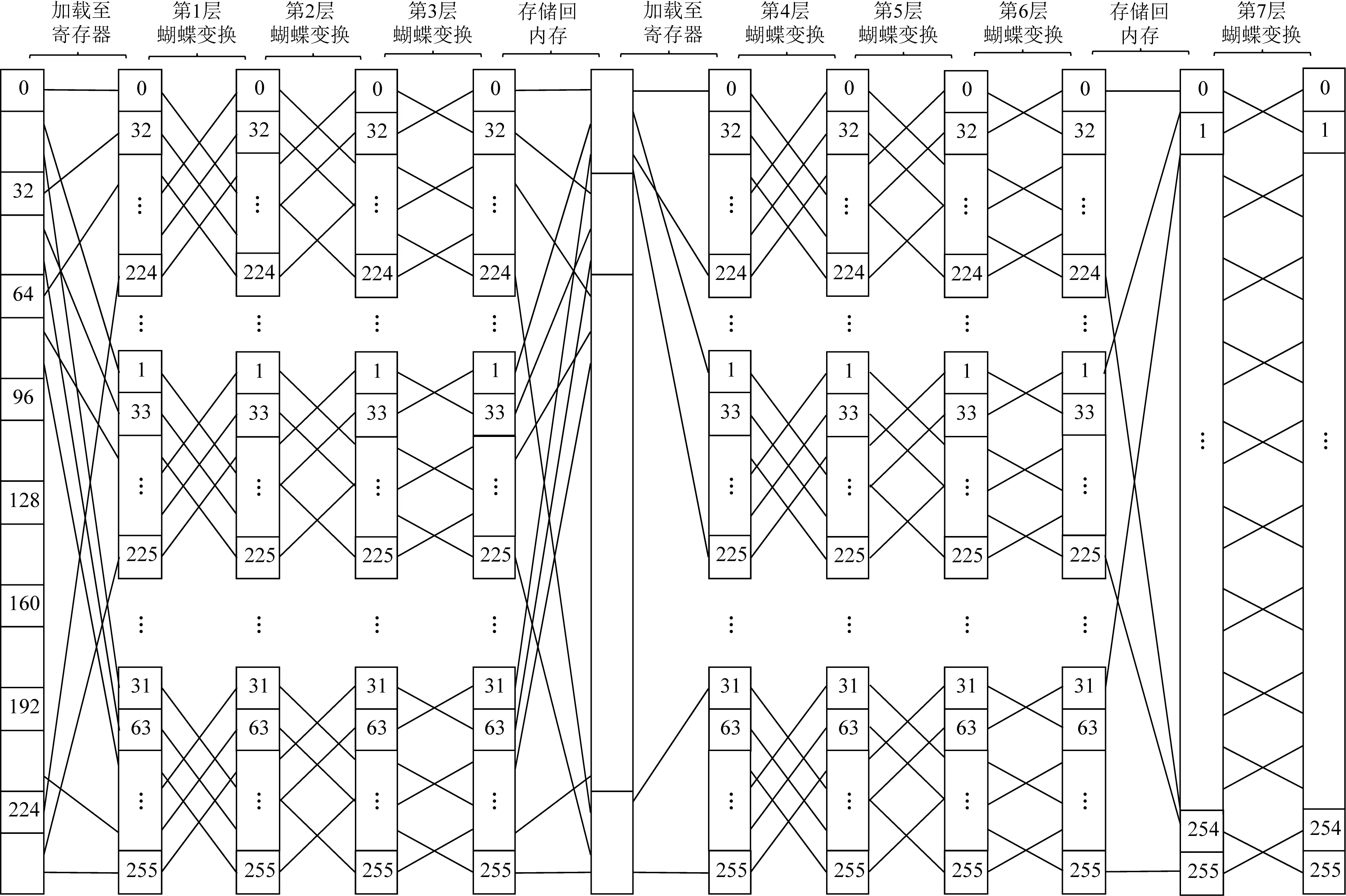
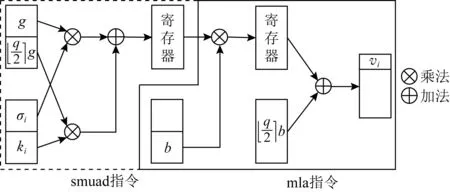
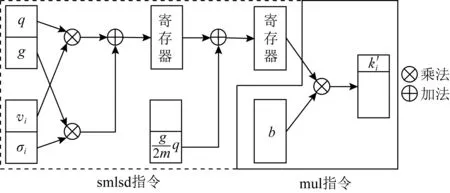
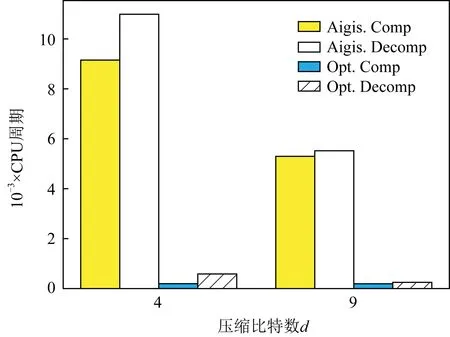
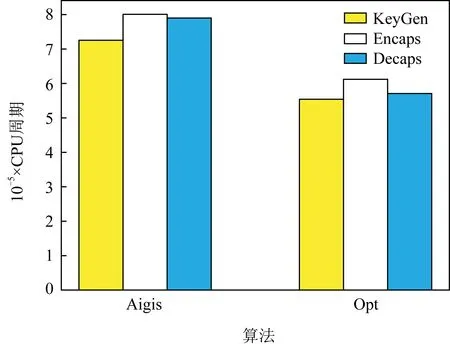
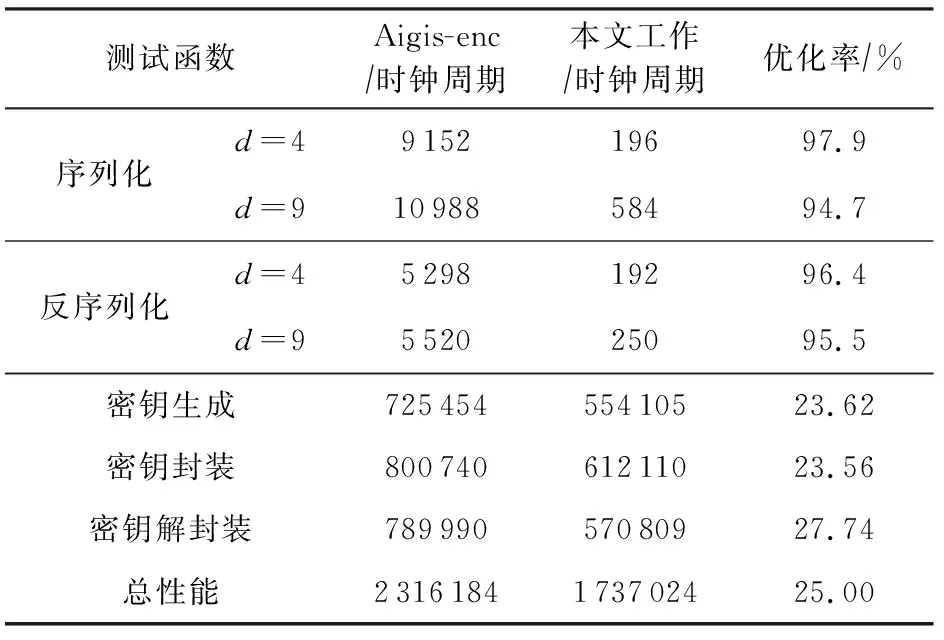
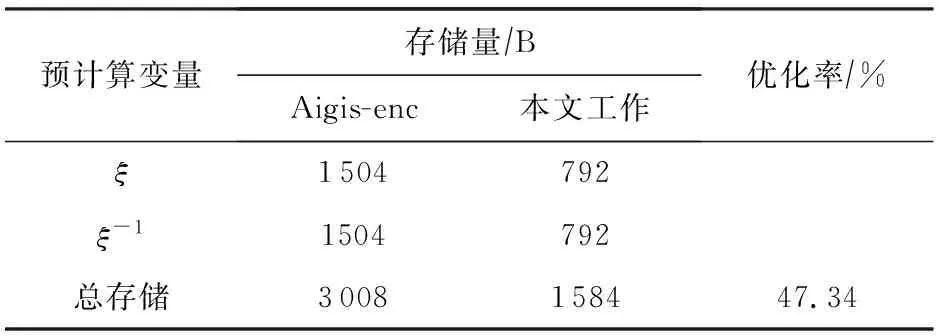
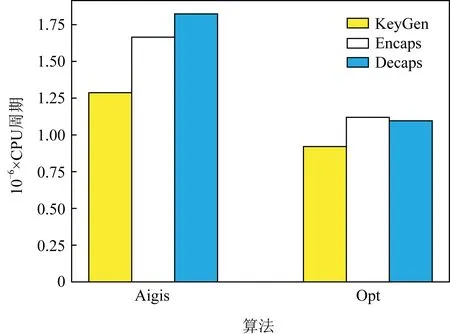
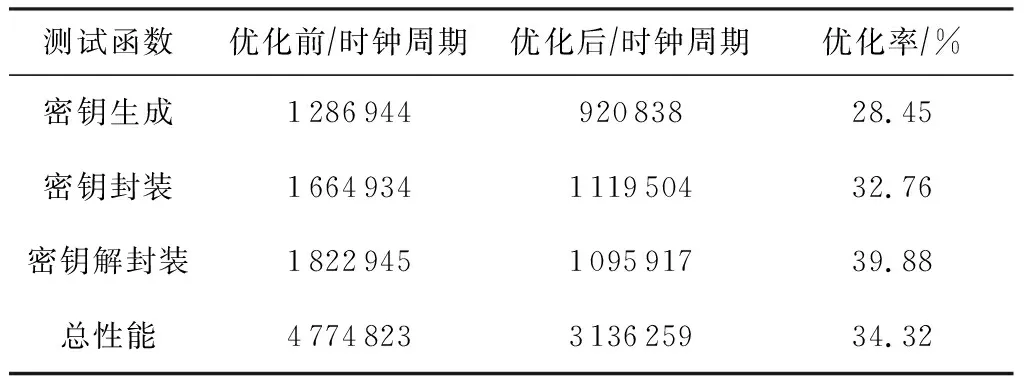
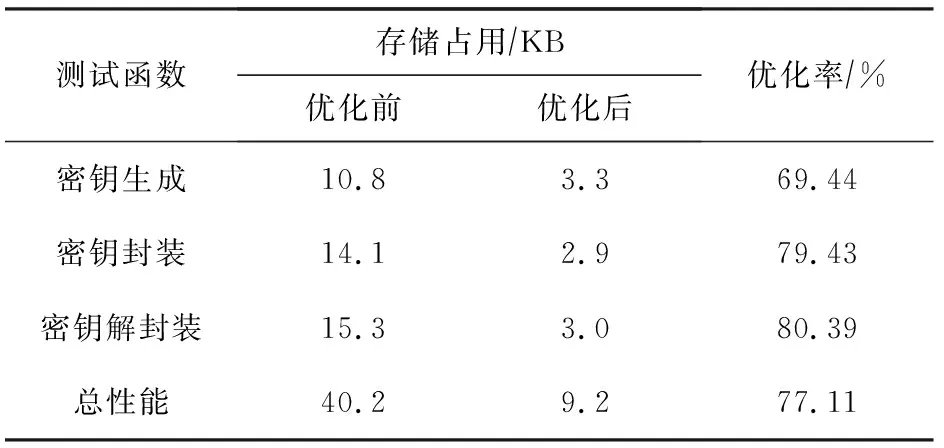
以β为基底,Barrett约减可实现[-β/2,β/2)区间的整数a至群Zq的规约,满足r=amodq,0≤r 算法4.有符号数Barrett约减算法. 输入: 16 b有符号整数a满足-β/2≤a<β/2、模数q满足q<β/2; 输出:r≡a(modq),其中0≤r≤q. ① functionBarrett(a,q) ④r=a-(tqmodβ); ⑤ returnr. ⑥ end function 3.2.2 Montgomery约减 不同于Barrett约减,Montgomery约减作用于基数为β的MONT域上.数据需从正常域转换到MONT域才可使用Montgomery约减. Montgomery约减的主要思想是通过对MONT域内的数加上模数q的倍数,转换取模时除法的除数,使得整除运算更容易进行.约减完成后再转换回正常数域.对于无符号数,约减结果在[0,2q)范围内,需要与q进行比较判断,以得到[0,q)范围内的输出.有符号数的Montgomery约减在原本的算法上进行了一些调整,输入范围为[-βq/2,βq/2),输出为(-q,q)范围内的有符号数,见算法5. 算法5.有符号数Montgomery约减算法. 输入:32 b有符号整数a满足-βq/2≤a<βq/2; 输出:16 b有符号整数r′满足-q ① functionMontgomery(a) ②m=aq-1mod±β; ⑤ returnr′. ⑥ end function 数论变换是快速傅里叶变换(fast Fourier transform, FFT)在有限域上的一种特殊形式,常用于实现Zq环上的多项式乘法加速.对于n长多项式,其中n为2的幂次,传统NTT要求参数q是满足2n|(q-1)的素数. c 逆向NTT定义为 且二者满足f=NTT-1(NTT(f)).给定f,g∈Zq[x]/(xn+1),NTT能够用来计算h=fg∈Zq[x]/(xn+1),矩阵形式的线性变换可表示为 算法6.多项式系数拒绝采样算法. ① functionParse(B) ②i,j0; ③ whilej ④dbi+256×bi+1; ⑤d ⑥ ifd ⑧jj+1; ⑨ end if ⑩ii+2; 基于MLWE困难问题构造的密钥封装方案,在实现中经常使用一些压缩和解压缩的方法,一方面,舍弃一些对正确性影响不大的低阶位可节省带宽和通信成本;另一方面,在加密和解密过程中执行LWE错误纠正.目前Aigis-enc[11]中使用的函数定义为 本文提出的针对Aigis-enc-768算法的AVX2优化方案主要包括3个关键点: 1) 模约减.使用汇编指令实现针对有符号数的改进版Barrett约减与Montgomery约减,结合二者提升约减效率; 2) 多项式乘法.采取删减一层的NTT,使用汇编指令实现并优化指令流水,以提升效率; 3) 多项式序列化处理.将压缩与解压缩中的除法运算替换为乘法与移位,从而可使用AVX2指令并行加速. 4.1.1 Barrett约减AVX2实现 Aigis-enc-768算法模数为q=7681,从而可将系数规模控制在16 b有符号数范围内.设定β=216,16倍并行的Barrett约减算法可使用4条指令实现,具体见算法7. 算法7.改进的Barrett约减算法的AVX2实现. 输入:向量化的16 b有符号整数a、常数模数q以及预计算的v和x; 输出:向量化的约减后的值r. ① functionBarrett_AVX2(a,q,v,x) ② vpmulhwt←av; /*计算av,取高16 b*/ ③ vpsrawt←t≫x;/*算术右移x位*/ ④ vpmullwt←tq; /*计算tq,取低16 b*/ ⑤ vpsubwr←a-t; /*计算a-t,得到结果*/ ⑥ returnr. ⑦ end function 4.1.2 Montgomery约减AVX2实现 在Aigis-enc-768实现中,Montgomery约减用于规约Montgomery域内2个16 b数的乘积,并保持其在Montgomery域内.根据模数设定β=216,实现步骤见算法8. 算法8.改进的Montgomery约减算法的AVX2实现. 输入:向量化的32 b有符号整数a,记为ahi和alo; 输出:向量化的16 b有符号整数r′. ① functionMontgomery_AVX2(a) ② vpmullwm←aloq-1; /*m=(aloq-1) mod±β*/ ④ vpsubwr′←ahi-t;/*r′=ahi-t*/ ⑤ returnr′. ⑥ end function Aigis-enc原始实现中采用了AVX2接口调用的形式,实现了(n,q)=(256,7681)的传统NTT.相比于API接口调用,直接使用AVX2指令实现具有更高的性能及指令调度安排灵活度,也可省略一些额外的调用消耗.另外,由于Aigis-enc三组参数中使用的q不统一,每个q对应的预计算表互不相同,导致算法需要开辟很多额外的存储空间.使用T-NTT,根的个数即可由n降低至n/2,减少了预计算表的空间需求. 根据分析,本文采用T-NTT,删减NTT运算的最后一层,并提供了AVX2指令集形式的汇编实现.AVX2实现中,先单独处理第0层,将系数a0,a1,…,a63和a128,a129,…,a191分别存入寄存器.通过指令vpmullw和vpmulhw进行蝴蝶变换,将系数与第1个单位根相乘,再通过指令vpaddw与vpsubw进行Montgomery约减,将系数约减至[-q,q]范围内.多项式剩余的128个系数,即a64,a65,…,a127和a192,a193,…,a255,也进行相同的处理.不同于第0层,第1~6层中,256个系数统一按序载入处理,乘以对应的单位根.在第4~6层中,需要使用PACK和UNPACK相关指令调整系数顺序,将相关的系数整合到一起.前向NTT采用了CT蝴蝶变换(Cooley-Tuckey butterflies),输入为正序多项式系数,输出为比特反转顺序的NTT域元素.逆向NTT采用了GS蝴蝶变换(Gentleman-Sande butterflies),输入为比特反转顺序的NTT域元素,输出正序多项式系数,其伪代码见算法9与算法10.通过这2种变换的组合可以省略位反转操作,以提高运行效率. 算法9.CT蝴蝶变换AVX2实现. 输入:向量化的16个低位系数rl、高位系数rh、模数q与单位根ζ; 输出:变换后的低位系数与高位系数向量rh′与rl′. ① functionCT_Butterfly_AVX2(rl,rh,q,ζ) ② vpmullwζq-1,rh,t1; /*t1=(rh×ζq-1)(mod 216)*/ ③ vpmulhwζ,rh,(rhζ)hi; ⑤ vpsubwt2,(rh×ζ)hi,(rh×ζ)′; /*(rh×ζ)′=(rh×ζ)hi-t2*/ ⑥ vpsubw (rh×ζ)′,rl,rh′; /*rh′=rl-(rh×ζ)′*/ ⑦ vpaddw (rh×ζ)′,rh,rl′; /*rl′=rh+(rh×ζ)′*/ ⑧ return (rh′,rl′). ⑨ end function 算法10.GS蝴蝶变换AVX2实现. 输入:向量化的16个低位系数rl、高位系数rh、模数q与单位根ζ; 输出:变换后的低位系数与高位系数向量rh′与rl′. ① functionGS_Butterfly_AVX2(r) ② vpsubwrh,rl,rh′;/*rh′=rl-rh*/ ③ vpaddwrh,rl,rl;/*rl=rl+rh*/ ④ vpmullwζq-1,rh′,t1; /*t1=(rh′×ζq-1) mod 216*/ ⑤ vpmulhwζ,rh′,rh′; ⑦ vpsubwt2,(rh′×ζ)hi,rh; /*rh=(rh′×ζ)hi-t2*/ ⑧ return (rh′,rl′). ⑨ end function 本节主要说明了多项式压缩并编码为字节流、字节流解码为多项式并解压缩这2个过程的优化方案,在算法中用于对公钥与密文进行处理.优化的主要难点在于除法运算的处理,由于AVX2指令集中不包含除法指令,Aigis-enc原始实现中尚未对其进行优化,这也造成了该过程较大的开销. Barrett在文献[25]中首次提出可以用一个乘法和一个移位运算来代替较为耗时除法运算,即 本节介绍了针对Aigis-enc-768算法的ARM Cortex-M4平台优化方案.设计中采取与第4节相同的改进方案,并结合该平台寄存器大小和Thumb与DSP指令集结构,对实现方案进行调整,从而最优化计算的速度与开销.另外,轻量级实现平台还需考虑片上存储,本文采用空间复用等方法减少了堆栈与存储资源的占用. 5.1.1 Barrett约减ARM实现 算法11描述了Barrett约减在ARM Cortex-M4上的实现,一次调用可完成2个16 b的约减. 算法11.Barrett约减算法ARM实现. 输入:封装2个系数的32 b寄存器单元a=ahi|alo; 输出:约减后的32 b寄存器单元r=rhi|rlo. ① functionBarrett_ARM(a) ② smulbbt1,a,v;/*t1←alov*/ ③ smultbt2,a,v;/*t2←ahiv*/ ⑥ smulbbt1,t1,q;/*t1←t1q*/ ⑦ smulbbt2,t2,q;/*t2←t2q*/ ⑧ pkhbtt,t1,t2,lsl#16 ⑨ usub 16r,a,t; /*rhi←ahi-thi,rlo←alo-tlo*/ ⑩ returnr. 5.1.2 Montgomery约减ARM实现 ARM Cortex-M4平台上多数指令执行时间均为一个时钟周期.调整算式结构以结合乘加运算,则可充分利用此特性,将一个乘法与一个加法替换为乘加运算,从而节省了一个周期的时钟消耗. 本文应用了改进后的Montgomery约减[22].算法的输入为2个16 b的有符号数alo与ahi,分别为2个32 b乘积的低字.输出为打包好的2个(-q,q)区间内的约减结果.将预存储的q-1调整为-q-1,则r′=ahi-t变更为r′=ahi+t,结合t计算中的乘法,即可使用smlabb指令在一个周期内完成2个16b的乘积与一个32b的加法.在Aigis-enc-768中,一个多项式向量由3个256维多项式构成,且2个多项式的乘法需要执行1 856次Montgomery约减(其中2次前向NTT需要896个,一次逆向NTT需要448个,向量点乘需要512个),改进后的方法可以大幅减少乘法所需的总时钟周期. 算法12.Montgomery约减算法ARM实现. 输入:封装2个系数的32 b寄存器单元a=ahi|alo; 输出:约减后的32 b寄存器单元r=rhi|rlo. ① functionMontgomery_ARM(a) ② smulbbt1,a,v; ③ smulbbr1,t1,-q-1; /*r1←(t1modβ) (-q-1)*/ ④ smlabbr1,r1,q,t1; ⑤ smultbt2,a,v; ⑥ smulbbr2,t2,-q-1; /*r2←(t2modβ) (-q-1)*/ ⑦ smlabbr2,r2,q,t2; ⑧ pkhbtr,r2,r1,asr#16; /*r←(r2hi|(r1hi≫16))*/ ⑨ returnr. ⑩ end function 本文使用了β=1的T-NTT,即删减最后一层.该方法大幅减小了预计算表存储空间,利于算法在嵌入式设备的部署.在AVX2实现中,由于寄存器存储空间充足,可加载完整的多项式并逐层变换.而ARM Cortex-M4为32 b架构,且资源受限(只有16个32 b寄存器),load与store一次只能存取2个系数,若采取如AVX2实现般逐层变换的方法,会引入过多的load与store指令,所以需要对NTT结构进行调整以适应平台特性,调整后的方案如图2所示: Fig. 2 Implementation of NTT on ARM Cortex-M4图2 ARM平台NTT实现 该方案的主要思想为以固定的距离拆分多项式,每次取16个系数存入8个寄存器,进行3层变换后存回原位置.举例来说,第一次循环存取的系数为r2={a1‖a0},r3={a33‖a32},r4={a65‖a64},…,r9={a65‖a64}.随后对其进行前3层数论变换,一对变换系数的距离间隔分别为128,64,32.变换结束后存回原地址,地址指针前进4 B,进入下一次循环.T-NTT第4~6层的操作同理进行,一对变换系数的距离间隔分别为16,8,4,最后统一执行系数间隔为2的第7层变换,得到最终结果.这里, 一个寄存器可以存放2个16 b的系数,相当于二并行加速. 本节中论述了多项式压缩与序列化在ARM Cortex-M4上的优化方案.优化时考虑的要素主要为: 1) 调整算式结构以尽可能结合运算过程,减少所需指令的数目; 2) 尽量在一个系数存在于寄存器的整个生命周期内进行尽可能多的运算操作,以减少load与store指令的开销. 为了达成这2个目标,需要在效率与寄存器容量2个指标之间权衡折衷.加密中将秘密消息编码、多项式压缩与序列化结合,即为算法2中的行⑦⑨,c2Compressq(v+Decompressq(msg,dm),dv);在解密中结合多项式反序列化、解压缩与消息解码,即算法3中的行③④,从而得到解密后消息msgCompressq(Decompressq(c2),σ).进而,本文结合除法运算转换法,对该运算顺序进行调整,使得DSP指令集中一些复合运算指令得以运用.优化后对单个位加密的核心过程见图3,解密核心过程如图4所示. Fig. 3 Implementation of encryption on ARM Cortex-M4图3 ARM平台加密核心步骤实现 Fig. 4 Implementation of decryption on ARM Cortex-M4图4 ARM平台解密核心步骤实现 这里加解密实现中均需对多项式进行预处理,通过指令pkhbt与pkhtb将σ与k同一索引位的系数封装入一个32 b的寄存器.继而,在加密中使用指令smuad与mla,解密中使用指令smlsd与mul以完成核心运算.此外,实现中还使用了位运算指令bfi与orr,已实现寄存器中位的提取与比特流的拼接. 嵌入式设备上存储空间是一重要瓶颈,算法空间使用情况也决定了其能否实际部署.考虑到这一要素,本文在保持性能尽可能不受影响的情况下,采取on-the-fly[22]计算与空间复用等优化思想,减小代码大小以及运行所需栈空间.本文对Aigis-enc-768的优化中以堆栈使用和速度为主要指标,同时保持代码大小的合理性. 5.4.1 栈空间资源复用 在Aigis-enc-768原始实现中,对方案涉及的所有元素都申请了空间,并且分别对其进行采样、存储.考虑到该运算的线性特性,各对多项式之间的乘法以及多项式内各系数的乘法均互相独立,内存中不需要同时存在多个多项式.由此,本文在实现中减少了空间申请,通过空间复用的方式完成多个多项式运算.具体来说,对于密钥生成和密钥封装,申请一个多项式变量与一个多项式向量变量,对于密钥解封装,申请2个多项式变量,每个多项式的运算都在此空间上进行,得到结果后即存入对应的密钥或密文位置. 基于模格的密钥封装方案在密钥生成与密钥封装中都包含A·s的核心运算,对此运算进行充分优化有利于降低代码运行空间需求.如3.3节所述,经过数论变换后1个多项式由128个一次多项式组成,它们之间的点乘互相独立,所以执行一次点乘仅需要一次多项式ai+ai+1x与si+si+1x相关的4个系数ai,ai+1,si与si+1,这就意味着矩阵A的系数可以需要时再采样,而不用全部生成后再读取.详细地说,由种子ρ扩展得到字节流后,一次只采样2个符合条件的系数,与s中的2个系数点乘,并存储回s的相应位置,从而省略了存储矩阵A所用的空间. 与之相同的还有噪音的采样.原始实现中,噪音采样函数输入为字节流,输出为服从中心二项分布的多项式.采用on-the-fly计算优化思想[22],噪音采样函数输入调整为字节流和多项式,每次采样噪音后即与输入多项式对应位置的系数相加,而不用再进行存储.但是这种方法也意味着不能对噪音多项式进行数论变换(因为NTT作用对象为一个完整的多项式),从而t′的计算方式由t′=A∘T-NTT(s)+T-NTT(e)调整为t′=T-NTT(T-NTT-1(A∘T-NTT(s))+e).这样会引入一个额外的NTT-1的消耗.在ARM Cortex-M4平台上,这意味着需要增加6944时钟周期,约占总运行时间的0.3%,但是可以节省矩阵A与多项式s,e共7 680 B的栈存储空间,权衡二者这样的消耗是值得的. 本文针对Aigis-enc密钥分装机制设计了AVX2与ARM Cortex-M4的优化方案,并于Aigis-enc-768算法上实现验证.本节介绍了2个平台的代码测试环境. 1) AVX2测试环境:本文进行AVX2测试的硬件环境为3.6 GHz的八核Intel Core i7-9700K和32 GB内存,且关闭了处理器的睿频加速技术(Turbo Boost)和硬件多线程技术(Hardware Multi-Threading);软件环境为macOS Big Sur 11.1操作系统与Apple clang 12.0.0.31.1编译器.使用的编译参数为-Wall -Wextra -Wpedantic -Wmissing-prototypes -Wredundantdecls -Wshadow -Wpointer-arith -mavx2 -mbmi2 -mpopcnt maes -march=native -mtune=native -O0 -fomit-frame-pointer -fno-stack-check. 2) ARM Cortex-M4测试环境:本文使用带有ARMv7E-M 指令集的STM32F4DISCOVERY开发板为测试平台,其内存为196 KB,闪存为1 MB,且最大频率为168 MHz. 本文采用CPU周期数作为衡量算法效率的标准,AVX2代码测试的CPU周期数为对应的函数执行10 000次后所得结果的中位数,ARM Cortex-M4上的结果为执行100次后的中位数. 图5与图6为Aigis-enc与本文AVX2实现效率的对比,其具体数值分别如表1所示. Fig. 5 Comparisons of polynomial compression and serialization betweenAigis-enc and our work图5 多项式压缩与序列化AVX2实现对比 Fig. 6 Comparisons of Aigis-enc and our work in AVX2 implementations图6 Aigis-enc与本文工作AVX2实现效率对比 图5为多项式压缩和序列化速度的比较,其中,压缩位数d=4的情形用于密文c中第2部分c2的生成,即计算c2Compressq(v+k,d),d=9用于生成密文的第一部分,即c1Compressq(u,d).本文设计中采取的方案性能将原始提升了97.9%和94.7%,相当于对原过程有47倍和19倍的加速. 图6是Aigis-enc与本文工作AVX2实现效率对比.如表1中时钟周期数所示,本文工作将密钥生成函数提升23.62%,密钥封装函数提升23.56%,密钥解封装函数提升27.74%,在总性能上体现为25.00%的加速,彰显了本文优化设计方案的作用效果. Table 1 Comparisons of Each Function of Aigis-enc and Our Work in AVX2 Implementations表1 Aigis-enc与本文工作AVX2实现效率比较 表2为Aigis-enc与本文AVX2实现NTT预计算表存储量的对比.在q=7 681下,为了适配AVX2指令实现,Aigis-enc扩展的预计算表总共需要3 008 B存储空间,而本文工作仅需1 584 B,减少了47.34%的存储. Table 2 Comparison of Precomputed Table Storage Between Aigis-enc and Our AVX2 Implementation表2 Aigis-enc与本文AVX2实现NTT预计算表 存储量对比 鉴于目前Aigis-enc仅提供了AVX2实现,且尚未有ARM平台或C参考实现方案,这里仅给出本文优化前后STM32F4DISCOVERY开发板上的实验测试结果来对比,如图7所示,具体数值如表3所示.其中,优化前的算法为根据Aigis-enc原始实现自主修改的C实现. Fig. 7 Comparison of implementation before and after optimization of Aigis-enc on ARM platform图7 ARM平台Aigis-enc优化前后实现效率对比 Table 3 Comparisons of Each Function of Aigis-enc and Our Work on ARM Cortex-M4 Platform 在栈空间占用上,原始实现密钥生成、密钥封装及密钥解封装分别占据10.8 KB,14.1 KB与15.3 KB,优化后达到3.3 KB,2.9 KB与3.0 KB,总体上有3.4倍的提升,如表4所示: Table 4 Menory Evaluation of Aigis-enc and Our Work on ARM Cortex-M4 Platform表4 Aigis-enc与本文工作在ARM Cortex-M4 平台上存储量测试 可见,采取改进的模约减算法、多项式乘法等优化方案,可大幅度提高ARM Cortex-M4上的实现效率. 本文给出了一种针对Aigis-enc算法的高效AVX2与ARM Cortex-M4实现方案,并选用Aigis-enc-768参数集进行实现验证.该实现方案在模约减、多项式乘法、序列化与反序列化等方面对Aigis-enc原始实现进行优化,同时大幅减少了代码尺寸、运行堆栈空间占用与预计算表存储需求,提升了算法总体性能,使其更易于实际部署,具有非常大的实际应用价值.

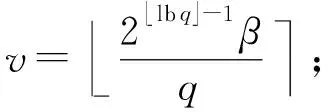
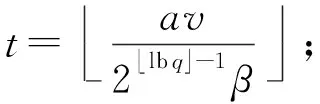
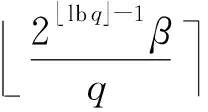
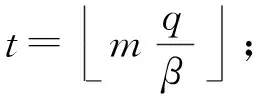
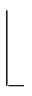
3.3 多项式乘法与数论变换
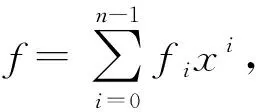
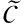
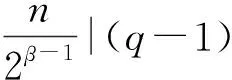
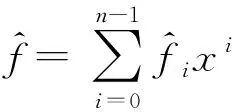
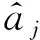
3.5 多项式压缩与解压缩


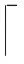
4 Aigis-enc算法AVX2高效实现方案设计
4.1 模约减



4.2 多项式数论变换改进


4.3 多项式序列化与反序列化优化


5 Aigis-enc算法ARM平台轻量级实现方案设计
5.1 模约减







5.2 多项式数论变换改进
5.3 加解密并行优化处理
5.4 存储空间及栈空间优化
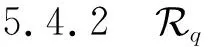
6 实验结果与性能比较
6.1 测试环境
6.2 AVX2实现性能比较
6.3 ARM实现性能与空间测试
7 总 结

