安全多方计算及其在机器学习中的应用
郭娟娟 王琼霄 许 新 王天雨 林璟锵
1(信息安全国家重点实验室(中国科学院信息工程研究所) 北京 100195) 2(中国科学院大学网络空间安全学院 北京 100049) 3(华控清交信息科技(北京)有限公司 北京 100084) 4(中国科学技术大学网络空间安全学院 合肥 230026)
安全多方计算(secure multiparty computation, MPC)起源于姚期智在1982年提出的百万富翁问题.在MPC中,参与方将各自的秘密数据输入到一个约定函数进行协同计算,即使在一方甚至多方被攻击的情况下,MPC仍能保证参与方的原始秘密数据不被泄露,并且保证函数计算结果的正确性.自MPC理论创立以来,已经衍生出多个技术分支,包括混淆电路、秘密分享、同态加密和不经意传输等.
混淆电路(garbled circuit, GC)是姚期智于1986年提出的安全两方计算协议[1],参与方在不知晓他人数据的前提下,使用私有数据共同计算一个用逻辑电路表示的函数.大多数混淆电路方案支持2个参与方计算,其性能优化集中于优化单个电路门的密文数量、传输的电路数量等.近年来多参与方计算的混淆电路方案相继提出.混淆电路的优点是能在恒定轮数内完成计算,只涉及开销较小的对称加密运算;缺点是通信量和电路大小呈线性关系,因此不适合计算复杂运算,只适用于比较大小等简单的逻辑运算.
秘密分享(secret sharing, SS)由Shamir[2]和Blakley[3]于1979年分别提出,数据拥有方计算秘密数据的份额并将其分发给计算方,计算方对不同秘密的份额计算,得到计算结果的份额.由于秘密拆分方式不同,秘密分享分为基于多项式插值的秘密分享和加性秘密分享(additive secret sharing).加性算术秘密分享能够计算线性运算、加性布尔秘密分享能够计算比较大小等非线性运算.加性秘密分享只需要进行简单的运算,计算开销小,在MPC中得到了广泛的应用.秘密分享的缺点是交互轮数和电路深度有关.
不经意传输(oblivious transfer, OT)由Rabin于1981年提出[4],消息发送方拥有多个消息,接收方获得其中某个值,发送方不知道接收方的选择信息.其衍生技术相关不经意传输(correlated oblivious transfer, COT)可以生成具有关系的随机数.OT,COT是重要的密码学组件,能够为GC传输导线标签、为SS生成相关随机数,只使用OT技术也能实现MPC协议.在OT的性能优化历程中,OT扩展(OT Extension)技术引入对称加密来降低计算开销,静默OT扩展(silent OT Extension)技术在本地扩展随机数种子来降低通信开销.
同态加密(homomorphic encryption, HE)的概念由Rivest等人[5]于1978年提出,可以在无需解密的情况下直接对加密数据执行计算.在发展过程中先后有部分同态加密方案与浅同态加密方案提出,直到2009年Gentry[6]构造出首个全同态加密方案.同态加密的优点是能以最小的通信成本设计轮数较优的MPC协议,缺点是乘法同态运算会带来较大的计算和存储开销,目前加法同态在实际中应用较多.
以上4类MPC技术在计算性能、通信效率和存储开销等方面都具有各自的优势和劣势,单一的MPC技术往往不能满足实际应用中计算复杂函数的需求,需要将多种MPC技术相结合才能获得性能均衡的实现方案.
目前MPC技术最典型的应用场景是隐私保护机器学习(privacy-preserving machine learning, PPML).MPC在模型训练和推理中可以保护用户数据和模型参数的隐私.近年来,Microsoft,Amazon和Google等公司提供“机器学习即服务”(machine learning as a service, MLaaS),即公司提供训练好的模型来对用户数据计算推断结果.模型数据是公司的重要资产,一旦泄露会带来重大的经济损失,同时用户也不愿意泄露私有数据,MPC能够在保护双方隐私的前提下完成模型推理.此外,在隐私保护法律法规GDPR,EFF和HIPPA等的约束下,不同机构间无法交换明文数据,MPC能够在保证数据集隐私的前提下来完成模型的训练.
PPML方案涉及多种类型的运算,考虑到参与方的数据规模不同、计算和网络能力不同、安全模型不同,可以在具体场景下组合多种MPC技术来实现PPML方案.
1 安全模型及目标
根据系统对敌手的容忍程度,MPC的安全模型可以分为半诚实安全模型(semi-honest model)和恶意安全模型(malicious model).
半诚实安全模型:敌手会按照协议规定进行运算,但试图通过协议中得到的信息挖掘其他参与方的隐私数据,该模型保证用户隐私信息不被敌手获得.
恶意安全模型:敌手不会遵守约定执行协议,会以错误的协议执行结果推断信息,恶意攻击行为也可以是任意的不可推理的.该模型中用户隐私数据不会被敌手获得,且不会因为敌手的恶意行为导致协议错误运行.在恶意安全模型中,要确保准确检测到敌手恶意行为会带来很大开销,因此提出了安全性和开销更均衡的隐蔽安全(covert)模型,能够在一定概率下检测到敌手恶意行为.公开可验证(public verifiable covert, PVC)方案在满足隐蔽安全条件的基础上,参与方生成公开可验证的欺骗证据,该模型适用于恶意行为被发现会遭受惩罚的现实场景.Covert模型和PVC模型通常只适用于GC和OT两种MPC技术.
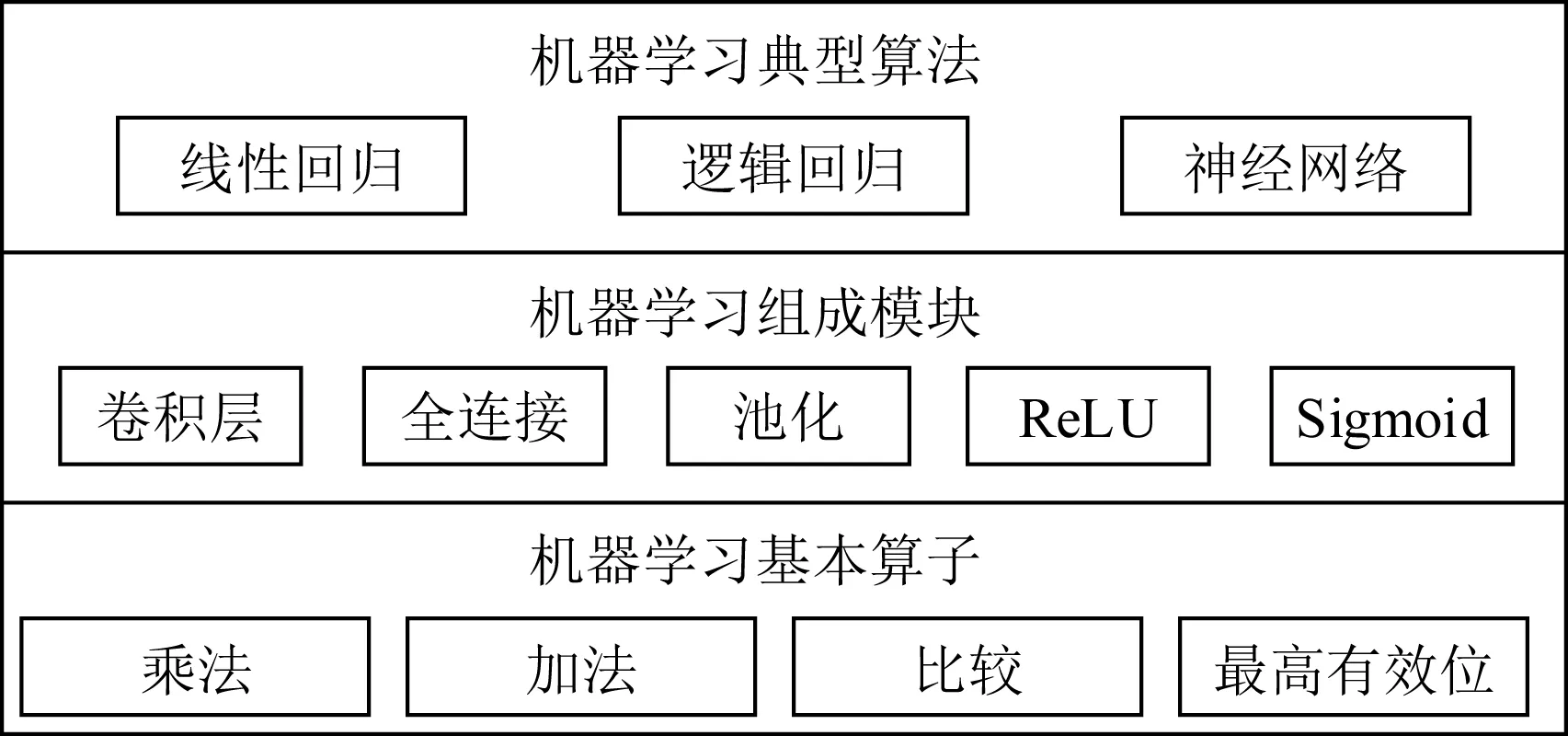
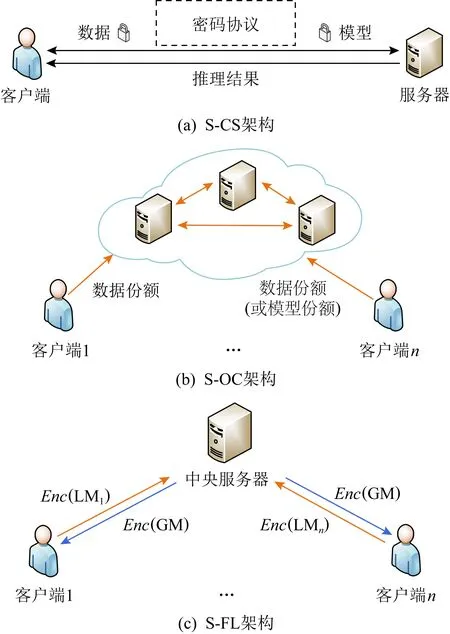
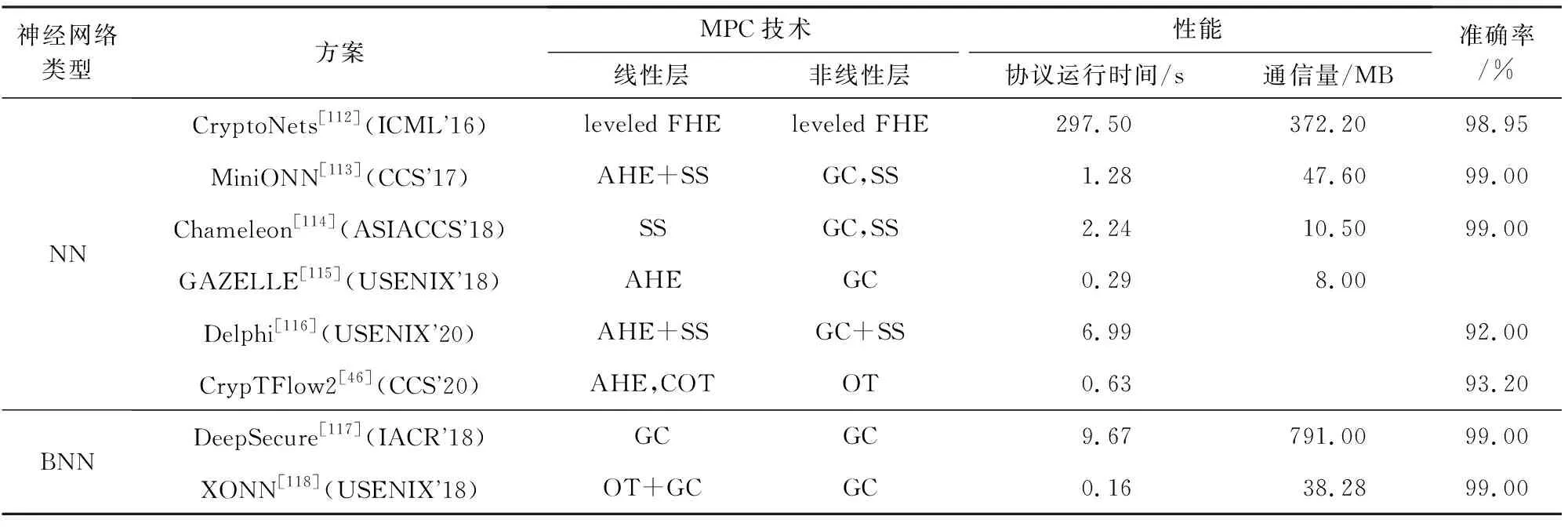
MPC的安全目标包括参与方数据隐私性和计算结果正确性等.进一步,对于参与方获得的计算输出结果,MPC协议能够达到的安全属性由强到弱依次为:保证结果输出(guaranteed output delivery, GOD)、公平性(fairness, FN)、一致中止(unanimious abort, UA)和选择中止(selective abort, SA).假设敌手可以控制t个参与方,诚实方占多数(honest majority)时门限值满足t 混淆电路(GC)技术最初关注两方参与的技术方案,技术发展分别从性能提升和安全性提升2方面展开,安全性主要体现在半诚实安全与恶意安全的区别,在具有同等安全的情况下,提升方案性能是解决GC实用性的重要研究方向.此外,随着MPC实际应用需求的增加,近年多方参与的GC方案研究也逐渐增多.本节将对两方参与的半诚实安全方案、两方参与的恶意安全方案及多方参与的方案分别进行介绍.图1展示了两方参与的GC技术发展脉络图. Fig. 1 Technological development of 2-party garbled circuit图1 两方参与的混淆电路技术发展脉络 2.1.1 半诚实安全两方混淆电路的性能优化 混淆电路是姚期智于1986年提出的一种电路加密技术,参与方混淆器(Garbler)和评估器(Evaluator)对各自的隐私输入计算目标函数,首先需要将目标函数转换成布尔电路的形式,布尔电路由多个二输入单输出的电路门级联而成.GC的构造是从单个电路门开始,先加密一个门再延伸到加密整个电路.GC工作流程如图2所示,以AND门为例,设电路门导线的索引为a,b和c,混淆器拥有导线a的输入值va,评估器拥有导线b的输入值vb.首先,在GC生成阶段,混淆器为所有导线选取随机数作为标签Lw,vw,下标w为导线索引,vw为导线取值,取值为0或1.按照真值表顺序依次使用输入标签加密输出标签得到4个密文,打乱密文排列顺序得到混淆表.然后,双方交互传输信息:混淆器向评估器发送混淆表、混淆器的输入标签La,va;评估器通过和混淆器执行OT获得自己的输入标签Lb,vb.最后,在GC评估阶段,评估器使用输入标签解密混淆表密文获得输出标签,当电路门是输出门时,评估器使用输出标签解密输出门密文得到明文输出.对于每个电路门,混淆器生成6个随机数、使用两重对称加密生成4个密文,评估器依次对4个密文解密直到解密成功为止.在整个过程中,GC的通信量取决于交互阶段双方传输的信息,包括混淆表、混淆器标签和OT传输评估器标签,主要的通信开销是混淆表.GC的计算开销来源于混淆器生成混淆表密文、评估器解密混淆表密文时的计算. Fig. 2 The diagram of garbled circuit图2 混淆电路工作流程 混淆电路提出至今,通信开销一直是其性能瓶颈,半诚实安全模型下的很多方案都致力于通过减少单个门的密文数量来降低通信开销. Beaver等人[7]于1990年提出的BMR方案构造了point-and-permute(p&p)方法,混淆器为输入导线w选取掩码比特λw,对导线真实值vw和掩码比特计算异或得到排列比特pw,vw,即pw,vw=vw⊕λw.混淆器在生成混淆表时,按照2个输入导线的排列比特对密文进行排列,并将排列比特和标签一起发给评估器.评估器解密时无需依次尝试4个密文,只需解密排列比特位置的密文即可获得输出标签,并且由于掩码比特是随机的,评估器不能根据排列比特推测出混淆器的真实输入,混淆电路的隐私性也得到了保证. Naor等人[8]于1999年提出了GRR(garbled row reduction, GRR),将单个电路门的密文数量从4个减少到3个.混淆器生成混淆表时,令混淆表中的第一个密文为0.若评估器要解密第一个密文,则对密文0解密获得输出导线标签.2009年Pinkas等人[10]提出的GRR2,进一步将密文数量降为2个,然而该方案使用多项式插值的方法实现,需要计算模幂运算,导致计算效率低. Kolesnikov等人[9]于2008年提出了Free-XOR,其计算XOR门的通信开销为0个密文,是目前计算XOR门的最优方案.混淆器选取全局随机数R,在生成GC时令每根导线2个标签取值相差固定值R,即Lw,1=Lw,0⊕R.评估器计算XOR门时将两方的输入标签异或得到输出标签,无需计算和传输混淆表,但是计算AND门时仍需要混淆表,因此Free-XOR适用于XOR门较多的运算.Kolesnikov等人[11]于2014年提出了FleXOR,计算AND门的方法与GRR2兼容,只需要2个密文,计算XOR门需要0~2个密文. Zahur等人[12]于2015年提出的半门(Half gates)是目前计算AND门的最优方案,该方案与Free-XOR兼容,计算AND,XOR门的通信开销分别为2,0个密文.Half gates将AND门转换为2个半门的异或,即c=a∧b=a∧(r⊕r⊕b)=(a∧r)⊕(a∧(r⊕b)).混淆器半门计算a∧r,评估器半门计算a∧(r⊕b),其中,混淆器拥有导线a的输入值va,评估器拥有导线b的输入值vb,令r=λb(λb为混淆器已知的掩码比特).在GC生成阶段,混淆器为混淆器半门生成2个密文H(La,0)⊕LGC,0,H(La,1)⊕LGC,0⊕λbR,对2个密文进行p&p和GRR处理后,混淆器半门的密文减少为1个;混淆器为评估器半门生成2个密文H(Lb,λb)⊕LEC,0,H(Lb,λb⊕1)⊕LEC,0⊕La,0,对2个密文做GRR处理后评估器半门的密文减少为1个,该半门无需做p&p处理,因为将评估器输入看作vb⊕λb,那么评估器拥有的vb则为排列比特.评估器获得混淆表和2个半门的输入标签La,va,Lb,vb⊕λb后,分别解密2个密文获得混淆器半门、评估器半门的输出标签LGC,LEC,将2个输出标签异或得到AND门的输出标签. Ball等人[13]于2016年提出Garbled gadgets可用于混淆算术电路和布尔电路.算术电路的实现是将Free-XOR从模2扩展到模m,此时每个导线w具有m个标签且相邻标签之间相差全局值R,该方案实现了无通信开销的模m的加法和常数乘法. 混淆电路的性能优化不仅包括对通信性能的优化,也有一些方案对于计算性能进行优化.早期GC通过对输入标签计算哈希、将哈希结果与输出标签异或来生成混淆表密文.英特尔内核的专用AES-NI指令用硬件加速了AES运算,激励Bellare等人[30]于2013年提出使用固定密钥AES实现的GC方案,比使用哈希算法实现的GC方案快50倍.此后大多数GC,OT方案都使用固定密钥AES实现,然而2020年Guo等人[31]发现很多GC方案在实现时因错误使用固定密钥AES而易受攻击,为此提出了安全使用固定密钥AES的方法并给出安全证明. 2.1.2 恶意安全两方混淆电路的性能优化 半诚实安全模型往往不能满足现实生活中的需求,恶意混淆器会做出发送错误的电路给评估器或通过错误地执行协议来推测评估器的输入等恶意行为.为此,一些抵御恶意敌手的混淆电路方案被提出,包括基于Cut-and-choose的混淆电路、可鉴别的混淆电路(Authenticated-GC)等.基于Cut-and-choose的混淆电路的性能优化目标是在满足特定安全条件时最小化传输电路的数量,通常只支持两方计算.Authenticated-GC将秘密分享技术应用于混淆电路中,并为秘密份额添加消息鉴别码,均衡了通信开销和交互轮数. 1) 基于Cut-and-choose的混淆电路 使用零知识证明技术来保证参与方正确执行协议会带来巨大开销.为了降低开销,Pinkas[14]于2003年首次将Cut-and-choose技术引入到GC中,Lindell等人[15]于2007年提出了第一个具有完整安全性证明的基于Cut-and-choose的恶意安全GC.在基于Cut-and-choose的GC中,混淆器生成σ(σ为复制因子)个GC并发送给评估器,评估器随机选择c个电路作为检测电路,剩余电路作为评估电路,恶意敌手攻击成功的概率为2-ρ(ρ为统计安全参数).评估器要求混淆器提供生成检测电路的随机数,来验证检测电路是否实现约定函数,检测通过后,按正常混淆电路的流程对评估电路进行计算以确定最终计算结果. 在基于Cut-and-choose的GC方案中,需要解决的问题是输入一致性问题(input consistency)和选择失败攻击(selective failure attack)问题.输入一致问题指的是恶意混淆器向评估器提供的σ个混淆电路的输入不一致,影响最终计算结果.选择失败攻击指的是恶意混淆器将电路门混淆表的其中一个密文篡改为错误的密文,如果这个密文刚好是评估器需要解密的密文,评估器在解密时检测到错误会退出,此时混淆器便会知道评估器的排列比特,进一步使用自己拥有的评估器的掩码比特计算出评估器的真实输入. 对于输入一致性问题,早期的工作[15]使用承诺方案来解决,通信开销较高.Shelat等人[16]于2011年提出一致性检测方法,通过传输少量参数代替零知识证明来降低通信开销.Lindell[20]于2016年提出输入恢复(input recovery)技术,当混淆器输入不一致导致评估器得到不同输出结果时,可以惩罚混淆器提供真实输入.Wang等人[21]于2017年提出在输出导线中编码陷门的方法,使得评估器在获得多个输出时可以恢复出混淆器的输入.此外,还有一些方案[17,32-33]也给出了解决输入一致性问题的办法. 对于选择失败攻击问题,文献[15]中评估器将真实输入与多个随机比特的异或值作为OT输入,使得评估器退出时与真实输入无关,混淆器无法通过选择失败攻击推测评估器输入.Shelat等人[34]通过构造探测矩阵降低了使用OT的数量,然而导致异或运算次数为评估器输入大小的平方,Wang等人[21]通过将评估器的输入分为多个块并构造更小的探测矩阵来减少计算开销. 基于Cut-and-choose的GC性能提升问题也受到广泛关注.Yan等人[18]于2014年提出了批处理(Batched)Cut-and-choose,两方对同一函数f(不同输入数据)进行N次安全计算时,批处理Cut-and-choose方案中的混淆器生成Nρ+c个电路,评估器随机选择c个电路作为检测电路,将剩余的电路随机分配到N个bucket中,每个bucket中包含计算一次f所需的电路,减少了每次计算的摊销成本.Lindell等人进一步对该技术进行了改进和实现[19,35].先前单一Cut-and-choose的复制因子为O(ρ),而批处理Cut-and-choose的复制因子为2+O(ρ/logN),可见其极大地降低了开销. 由于将Cut-and-choose应用于整个电路开销很大,于是Nielsen等人[22]2009年首次提出应用于电路门的Cut-and-choose方案LEGO,该方案中混淆器构造大量NAND门,双方对这些电路门执行批处理Cut-and-choose,评估器随机选择部分电路打开检测正确性,将剩余门随机分配给bucket并集成到混淆电路中.评估器在评估电路时,取出bucket中大多数输出作为该门的输出.LEGO使用了Pederson同态承诺,导致效率较低,Frederiksen等人[23]于2013年提出的MiniLEGO采用基于OT的异或同态承诺协议,Frederiksen等人[24]于2015年提出的TinyLEGO通过优化bucket的构造来提高通信效率.Kolesnikov等人[25]于2017年提出的DUPLO可以对任意电路组件进行Cut-and-choose,电路组件的大小范围可以是单个电路门到整个电路.Zhu等人[26]于2017年提出的JIMU通过使用异或同态哈希来代替先前的异或同态承诺. 公开可验证(PVC)安全最早于2012年提出,阿里巴巴[36]于2019年首次实现了公开可验证的混淆电路,该方案使用Cut-and-choose的方法来实现,混淆器发送多个电路给评估器,评估器选择一个电路用于评估,剩余电路用于检测.每个参与方的所有行为都自动带有类似签名的机制以供其他参与方存证,当发现恶意行为时将其签名公开,令恶意参与方承受名誉损失,以此来威慑理性的参与方正确执行协议. 2) 可鉴别的混淆电路 先前的方案均存在一定局限性:对整个电路实施Cut-and-choose的通信、计算开销大;对电路门实施Cut-and-choose的运行时间长;恶意安全秘密分享协议的交互轮数多等.针对现有协议的不足,Wang等人[27]于2017年提出恒定轮数的可鉴别混淆电路Authenticated-GC.为了解决选择失败攻击问题,该方案引入预处理程序将导线掩码比特拆分为2个份额,将其分别分发给混淆器和评估器,然而掩码比特拆分后导致混淆器无法独立地生成混淆表,需要混淆器和评估器这2个参与方分布式地生成混淆表.由于混淆器可能构造错误的混淆表份额影响最终计算结果,该方案引入BDOZ型MAC[37]使得双方可鉴别对方混淆表份额的正确性. Authenticated-GC方案中混淆器和评估器协同生成混淆电路,预处理程序包括“与计算函数无关的预处理”和“与计算函数有关的预处理”.“与计算函数无关的预处理”为混淆器和评估器生成全局密钥、输入导线掩码比特的份额及对应的MAC,混淆器和评估器可以在本地计算出XOR门的输出导线掩码比特及MAC.然而计算AND门时,需要“与计算函数有关的预处理”生成AND三元组,即预处理程序根据从混淆器和评估器收到的输入导线掩码比特计算输出导线的掩码比特,并返回给混淆器和评估器,然后两方使用各自的份额生成混淆表份额.在数据输入阶段双方对彼此的掩码比特鉴别通过后再执行OT传输标签,在电路评估阶段评估器逐层使用输入导线标签计算输出导线标签及鉴别信息,在电路输出阶段评估器鉴别输出导线MAC正确后使用标签解密GC获得结果. Katz等人[28]于2018年提出安全两方计算场景下Authenticated-GC的优化方案,通过设计与半门方案兼容的可鉴别混淆电路、避免每次混淆都发送MAC以及优化AND门的三元组来提高计算和通信效率. 2.1.3 多方参与的混淆电路 1) 基于BMR的多方混淆电路 为了能够让多个参与方协同地生成混淆电路,Beaver等人[7]于1990年提出BMR协议,将姚氏混淆电路扩展到多方场景,各参与方为每条导线生成加密值,对所有参与方生成的同一导线的加密值计算异或,得到该导线最终的加密值. 原始BMR方案只能抵御半诚实行为敌手,但与其他安全计算技术(SPDZ,SHE和OT)合用可以抵御恶意行为敌手.最初BMR使用零知识证明技术来证明生成导线加密值时正确使用了伪随机函数(pseudo random function, PRF),计算开销较大.SPDZ-BMR[38],SHE-BMR[39]和OT-BMR[40]对PRF的证明和检查有所不同:SPDZ-BMR在评估电路时使用SPDZ型MAC来检查PRF值和密钥;SHE-BMR使用SHE来验证PRF值的正确性;OT-BMR使用COT来对PRF值进行一致性检查.SPDZ-BMR,SHE-BMR和OT-BMR中每个门的通信开销依次为O(n4κ),O(n3κ),O(n2B2κ),其中B=O(1+ρ/log|C|).可见2017年提出的OT-BMR为这几个方案中性能最优的方案. 2017年Wang等人[41]将可鉴别混淆电路方案与BMR技术结合,设计了多方混淆电路方案,通信开销为O(n2Bκ).Yang等人[29]于2020年进一步提出优化方案,针对文献[27]中“与计算函数有关的预处理”进行改进,优化了AND三元组生成方式,并首次提出将半门方案应用于多方场景,其中三方计算“与计算函数有关的预处理”的通信效率提高了35%. 2) 三方混淆电路 实际应用中也存在少数参与方计算混淆电路的场景,例如只有3个参与方.安全三方计算通过秘密分享实现的方案较多,混淆电路也有少量专门支持3个参与方的方案,通常包含2个混淆器以及1个评估器,评估器通过2个混淆器生成的电路一致性来判断是否有恶意行为.CKM+14[42]将Cut-and-choose应用于三方混淆电路,评估器P3的输入通过XOR拆分为多个份额,混淆器P1,P2基于BMR协作生成GC,评估器P3分别和P1,P2通过Cut-and-choose的方式验证双方生成GC的正确性.MRZ15[43]需要2个混淆器协商一致的随机数来生成混淆电路,能够容忍一个恶意混淆器,评估器采用秘密分享拆分其输入并从2个混淆器得到输入份额的标签,进一步恢复出真实输入的标签,该方案仅使用对称加密而无需使用OT,从而提高了计算效率.MRZ15之后被应用于混合计算框架ABY3,可以与三方秘密分享技术进行转换. 不经意传输(OT)是密码学的基本协议原语之一,由Rabin于1981年提出.OT技术主要包括OT,OT扩展以及相关不经意传输(COT).OT在MPC场景中有广泛的应用:OT自身可实现多项式计算[44-45]和比较大小[46];OT作为重要的MPC安全组件可与其他MPC技术结合应用,例如OT在混淆电路中承担着传输标签的任务;COT能够为秘密分享方案生成相关随机数[47]、消息鉴别码等. Fig. 3 The technic of oblivious transfer图3 OT技术原理 Even等人[48]于1982年提出1-out-of-2 OT的概念,如图3(a)所示.发送方Alice输入2个消息m0,m1,接收方Bob输入选择比特b,OT向Bob输出mb,协议执行过程中Alice不能获知选择比特b且Bob不能获知m1-b.OT可以由基于不同安全假设的公钥加密算法来实现,包括基于DDH实现的NP01[49]、基于LWE实现的BD18[50]和MR19[51]等. 然而使用非对称密码算法生成大量的OT会带来很大的计算开销,并且Impagliazzo等人[52]于1989年证明无法在不使用公钥密码的情况下实现OT.为了降低计算开销,研究者们提出了OT扩展技术,使用混合加密方式来生成OT,即先使用少量的公钥算法生成对称密钥,再进一步使用对称加密来完成消息的不经意传输. 1) OT扩展 Beaver[53]于1996年首次提出OT扩展,使用κ(κ为计算安全参数)个基础OT(base OT)可以生成κ的多项式个OT,但是该方案需要使用GC计算复杂的伪随机数发生器导致效率很低. 在基础OT阶段,Bob复制κ份选择向量r得到m×κ维矩阵R,然后选取m×κ维随机矩阵T并计算T′=T⊕R.Alice和Bob互换原本的发送方和接收方身份提供输入:Bob作为发送方输入矩阵T,T′,Alice作为接收方输入长度为κ位的随机比特串s.基础OT执行结束后Alice获得输出矩阵Q,该矩阵第i列(1≤i≤κ)满足Qi=(si·r)⊕Ti,第j行(1≤j≤m)满足Qj=(rj·s)⊕Tj. 恶意接收方Bob可以在基础OT阶段使用不同的选择向量来同时获得发送方Alice的2个消息,因此需要对接收方的输入进行一致性检测来发现恶意行为.IKNP03在半诚实协议的基础上,引入了Cut-and-choose技术来在OT扩展阶段检测Bob输入的一致性,这种检测方式带来了很大的开销. 研究者们提出了一系列半诚实模型下OT扩展的性能优化方案.Asharov等人[55]于2013年提出的方案ALSZ13分别设计了相关不经意传输(COT)扩展和随机不经意传输(Random OT, ROT)扩展.COT中发送方拥有的输入消息是相关的,例如Free-XOR的标签传输;ROT中发送方拥有的消息不相关的.Kolesnikov等人[56]于2013年提出的方案KK13适用于传输短秘密值,该应用场景包括GMW的AND运算等.KK13改变了IKNP03中选择向量r的重复编码方式,Bob对r采用随机编码后可在OT扩展阶段获得1-out-of-nOT.当传输的短消息长度为1位时KK13比IKNP03的通信效率提高O(logκ)倍.由于KK13方案里n取值上限为256,Kolesnikov等人[57]提出方案KKRT16对其进行改进,Bob通过使用PRF对r编码,实现了1-out-of-∞ OT扩展.Boyle等人[58]于2019年提出的方案BCG+19b基于伪随机关系随机数生成器(pseudorandom correlation generator, PCG)实现了静默OT扩展,使用PCG实现静默预处理时,参与方之间只需要少量通信来生成随机数种子,然后在本地对短随机数种子进行扩展来生成具有关系的长随机数.BCG+19b中生成一个OT平均只需要0~3位的通信开销,极大地降低了OT扩展的通信量,但是其轮数复杂度高,适用于通信带宽资源受限的场景. 此外,还有一些方案用来提高恶意安全模型下OT扩展的效率.由于基于Cut-and-choose实现的一致性检测方案[59-60]性能太差,Nielsen等人[61]于2012年提出另一种一致性检测的方法NNOB12,使用哈希函数在基础OT阶段对Bob的选择向量r进行一致性检测,实现该方案需要2.7κ个基础OT.ALSZ15[62]在NNOB12的基础上进行改进,将基础OT数量减少为κ+ρ.KOS15[63]在IKNP03半诚实安全方案的基础上改进协议,在OT扩展阶段对接收方输入向量进行一致性检测.在KOS15中,Alice和Bob协商一个行数索引集C,接收方Bob计算T*=⊕j∈CTj和R*=⊕j∈CRj并发送给发送方Alice,然后Alice计算T*⊕(R*·s)并检查Q*=T*⊕(R*·s)是否成立,若不成立则退出协议.KOS15仅需κ个基础OT,与IKNP03半诚实安全方案相比并未引入额外的开销.3个方案NNOB12,ALSZ15和KOS15都实现了恶意安全的1-out-of-2的OT扩展,OOS16[64]方案在KK13的基础上加入与KOS15类似的一致性检测获得恶意安全的1-out-of-nOT扩展(n≤276),该协议只需要κ个基础OT,运行时间比KK13增长约20%. 2) 相关不经意传输 相关不经意传输(COT)最早在ALSZ13中提出,其功能是生成相关的随机数.COT的流程如图3(c)所示,发送方的输入为r,r⊕Δ,接收方的输入索引为b,COT向接收方输出r⊕Δb.向量不经意线性评估(vector oblivious linear-function evaluation, VOLE)是COT的广义定义,接收方可以获得发送方所持有信息的线性组合. KOS15提出可以使用COT来实现OT扩展中的基础OT协议.Boyle等人[65]于2018年提出的方案BCGI18基于LPN假设构造了半诚实安全的VOLE,通过PCG在本地生成关系向量.Boyle等人[66]于2019年提出的BCG+19a生成分布式密钥时使用可穿孔的伪随机函数(puncturable pseudorandom function, PPRF)代替BCGI18中的分布式点函数(distributed point function, DPF),并且通过安全设置PPRF密钥将协议的安全性提升为恶意安全性,该方案的通信开销比IKNP03减少1 000倍,计算效率只提高了6倍.Schoppmann等人[67]的并行工作SGRR19基于primal-LPN实现了半诚实安全的VOLE协议,通信效率只比IKNP03提高20倍,计算效率高于BCG+19a.Ferret20[68]基于SGRR19改进了VOLE方案,实现的半诚实安全方案将通信开销减少15倍.在半诚实方案的基础上引入一致性检测实现恶意安全性,平均每个COT的运行时间比半诚实安全方案慢1~3 ns. 以上COT方案中,BCG+19a和Ferret基于VOLE实现了OT扩展,而SGRR19没有实现OT扩展. 表1对OT扩展方案从安全模型、轮数、通信量和运行时间等方面进行对比.其中,κ取值为128,N为比特向量位数,通信量、运行时间为生成1个OT时的平均通信量、平均运行时间.通过对比得出BCG+19a为目前通信效率最好的方案,Ferret20为目前计算效率最好的方案. Table 1 Comparison of OT Extension Schemes表1 OT扩展技术性能对比 传统的秘密分享方案中,秘密分发者将秘密拆分为份额并分发给参与方,只有足够数量的秘密份额组合在一起才能够恢复出秘密信息.基于秘密分享的安全多方计算(secret sharing-secure multiparty computation, SS-MPC)指的是参与方对不同秘密数据的份额进行运算,得到计算结果的份额,足够数量的结果份额组合在一起能够恢复出计算结果.本节围绕SS-MPC来展开介绍,而不关注SS技术本身. SS-MPC根据秘密的生成方式可以分为基于多项式插值的秘密分享和加性秘密分享.基于多项式插值的SS-MPC容易实现任意门限,但是需要模幂运算,导致其计算效率低.加性秘密分享根据秘密数据形式可以分为算术秘密分享和布尔秘密分享,在计算线性运算时通常需要使用算术秘密分享,在计算非线性运算时通常需要使用布尔秘密分享.加性秘密分享的优势是计算效率高,其门限方案的实现需要参与方持有冗余份额.目前SS-MPC在实际中应用最广泛,能够高效地实现线性运算和非线性运算. 2.3.1 SS-MPC计算线性运算 SS-MPC根据系统中敌手控制的参与方数量,可分为诚实方占多数的SS-MPC和不诚实方占多数的SS-MPC. 1) 诚实方占多数 SS-MPC在早期有一些经典方案.GMW方案[69]于1987年被提出,能够支持多个参与方进行布尔运算,秘密数据以异或的形式拆分,计算XOR运算可在本地完成,计算AND运算需要参与方两两之间执行1-out-of-4 OT,导致交互轮数较多.BGW方案[70]于1988年被提出,是基于Shamir秘密分享实现的SS-MPC方案,但其计算乘法要用到随机化和降阶处理,导致开销较大.Beaver三元组[71](Beaver triples)于1991年被提出,是SS-MPC中最常用的乘法组件.该方案在预处理阶段选取随机数a,b和c,满足c=ab,并为其生成加性份额ai,bi和ci(1≤i≤n).在线阶段,参与方Pi拥有秘密数据x,y的加性份额xi,yi,Pi在本地计算xi-ai,yi-bi并广播;收到其他参与方广播的份额后Pi将份额相加得到x-a,y-b,然后对已有数据计算得到积的份额zi=(x-a)bi+(y-b)ai+ci.秘密恢复阶段,每个参与方提供zi,对zi求和再与(x-a)(y-b)相加便能恢复出xy. 近年来由于机器学习等应用场景的需要,涌现出基于SS-MPC实现的PPML方案,包括ABY3和SecureNN等.这些方案的底层协议是加法、乘法和比较等基本算子的SS-MPC协议,高层协议实现了机器学习模块的隐私保护,本节主要关注这些方案的底层协议.由于加法运算在本地对份额相加即可,乘法运算的流程相对复杂,因此主要对乘法运算进行分析. SS-MPC最初提出时交互轮数多、通信量也较大,大多数SS-MPC方案都是对这2个指标进行优化.优化方法主要包括引入相关随机数、将计算前移到预处理阶段以及增加计算方的数量等.为了解决计算方的单点失效问题,一些方案构造了门限秘密分享来提高系统容错能力. 2008年提出的Sharemind[72]设计了半诚实安全的三方SS-MPC方案.秘密分享的过程为:数据拥有方对数据x,y计算加性份额xi,yi(i=1,2,3)并分发给计算方Pi.计算乘法的过程为:Pi在本地计算xiyi,3个计算方交互计算得到交叉项xiyj(i,j=1,2,3).例如计算交叉项x1y2,P3选取随机数a1,a2并分别分发给P1,P2,然后计算w3=a1a2作为自己的份额;P1和P2分别计算x1+a1,y2+a2并发送给对方,然后P1,P2通过计算分别得到份额w1=-a1(y2+a2),w2=y2(x1+a1).至此,每个Pi分别得到交叉项x1y2的份额wi,满足w1+w2+w3=x1y2,其他交叉项的计算同理.最终Pi将自己的本地份额与交叉项份额相加得到xy的份额. 为了降低Sharemind的轮数和通信量,2016年Araki等人提出的方案AFL+16[73]引入相关随机数,并通过设置冗余秘密份额构造了半诚实安全的2-out-of-3 SS-MPC方案.该方案设计了算术、布尔2种秘密分享方案,以算术秘密分享为例,秘密分享的过程为:数据拥有方选取3个和为0的l位长随机串a1,a2,a3,满足a1+a2+a3=0,然后计算秘密数据x的加性份额xi=ai-1-x(i=1,2,3),令i=1时i-1=3,同理可计算秘密数据y的加性份额.数据拥有方向计算方Pi分发份额(ai,xi),(bi,yi).计算乘法的过程为:Pi选取随机数αi,计算ri=(xiyi-aibi+αi)/3并将ri发给Pi+1,其中α1+α2+α3=0;收到其他参与方的信息后,Pi计算积的份额(ci,zi):ci=-ri-1-ri,zi=-2ri-1-ri.秘密恢复时任意2个计算方可以恢复出xy. 2018年提出的ABY3[74]受到AFL+16设置冗余份额的启发,基于此设计了新的2-out-of-3 SS-MPC方案,进一步通过份额校验实现了恶意安全方案.秘密分享的过程为:数据拥有方计算长度为l位的秘密数据x,y的加性份额xi,yi(i=1,2,3),并向3个计算方Pi分发份额(xi,xi+1),(yi,yi+1).计算乘法的过程为:Pi在本地计算得到积的份额zi=xiyi+xiyi+1+xi+1yi+αi并将其发给Pi-1,其中α1+α2+α3=0.在秘密恢复阶段,任意2个计算方可以恢复出xy.ABY3通过使用Beaver三元组来完成份额校验,实现的恶意安全方案最多能够容忍一个恶意参与方. 为了降低ABY3在线阶段的通信量和交互轮数,2019年提出的ASTRA[75]将一个计算方的运算前移到预处理阶段进行.秘密分享的过程为:在离线阶段数据拥有方P0同时也是计算方,分别与计算方P1,P2使用PRF生成2个随机数rx,1,rx,2,在线阶段P0计算秘密数据x的份额mx=x+rx并发送给P1,P2,其中rx=rx,1+rx,2,P1,P2分别设置x的份额为(mx,rx,1),(mx,rx,2),秘密y的份额同理可得.计算乘法的过程为:离线阶段P0和P1生成随机数rz,1,rxy,1,P0和P2生成随机数rz,2,rxy,2,满足rxy,1+rxy,2=rxry.在线阶段的计算过程中,2个计算方Pi(i=1,2)分别计算mz,i=(i-1)×mxmy-mxry,i-myrx,i+rz,i+rxy,i,双方交换份额相加得到mz=xy+rz,1+rz,2,设置份额为(mz,rz,i).在秘密恢复阶段,任意2个计算方可以恢复出xy=mz-rz,1-rz,2.ASTRA的恶意安全方案在半诚实安全方案的基础上加入一致性检测,在输入和输出阶段通过对比份额的哈希值来检查份额一致性,在计算阶段使用Beaver三元组验证正确性. 2020年提出的BLAZE[76]对ASTRA中一致性检测的预处理过程进行改进,将其通信量减少1/7.同年,TRIDENT[77]用另一种思路来提升ASTRA的性能,设计了四方秘密分享方案,在线阶段需要3个参与方两两之间会生成积的份额及其哈希值,并发给另一方检验一致性. SecureNN[78]是2019年提出的半诚实安全三方及四方SS-MPC方案.数据拥有方生成m×n维秘密矩阵x,n×v维秘密矩阵y的加性份额xi,yi(i=1,2),并分发给计算方P1,P2,矩阵元素是长度为l位的比特串.三方秘密分享方案中计算乘法时采用Beaver三元组的思想,P0作为辅助节点来生成Beaver三元组以及其他随机数,P1和P2是计算节点.四方秘密分享方案中P1,P2是计算节点,P3,P4是辅助计算节点.计算乘法运算时首先P1,P2分别在本地计算x1y1,x2y2;然后,P1分别把x1,y1发给P3,P4,P2分别把y2,x2发给P3,P4;收到份额后,P3,P4分别计算交叉项x1y2,x2y1并发送给P1,P2.在秘密恢复阶段,将P1和P2拥有的份额相加即可恢复出矩阵xy. 2) 不诚实方占多数 在恶意安全的SS-MPC方案中,可以通过向秘密份额添加消息鉴别码,来检测计算过程中计算方是否存在篡改行为.这类方案主要包括BDOZ和SPDZ等,能够用于不诚实方占多数的场景,达到了中止安全性,即发现参与方恶意行为时中止协议. Bendlin等人[35]于2011年提出了BDOZ消息鉴别码,在2个参与方的场景下,P1,P2分别拥有全局密钥Δ1,Δ2,以及秘密x的加性份额x1,x2.秘密x的BDOZ份额用[x]来表示,P1拥有[x]1=(x1,M1,K1),P2拥有[x]2=(x2,M2,K2).其中K1,K2是MAC密钥,M1,M2是MAC值,满足关系M1=K2+Δ2x1,M2=K1+Δ1x2.鉴别P1的份额x1时,P1向P2提供(x1,M1),P2使用(K2,Δ2)验证等式M1=K2+Δ2x1是否成立,若等式成立则鉴别通过,鉴别P2的份额同理.BDOZ可以扩展到n个参与方的场景,但是每个参与方都需要对其他n-1个参与方的MAC密钥分别生成一个MAC,存储开销和参与方的数量成线性关系. 为了解决BDOZ中的存储开销问题,Damgård等人[79]于2012年提出另一种消息鉴别码SPDZ,每个参与方只存储恒定数量的MAC.SPDZ型MAC表示为M(x)=α×x,其中α为MAC全局密钥、x为秘密数据.在SPDZ方案中,每个参与方Pi(1≤i≤n)持有密钥α的加性秘密份额αi,x的加性秘密份额xi和MAC值M(x)的加性秘密份额M(x)i.验证MAC时需要先恢复出x,α和M(x)再检查等式M(x)=α×x是否成立.SPDZ型MAC满足加法、常数乘法的同态性,计算乘法时需Beaver三元组协助来验证份额.具体实现时,SPDZ在预处理阶段使用FHE生成Beaver三元组和MAC,并使用零知识证明保证FHE密文的正确性. Damgård等人于2013年提出SPDZ的改进方案[80],该方案在验证MAC时无需恢复MAC密钥,因此可以继续对还未验证的秘密数据进行计算.验证MAC时各参与方首先广播xi,收到广播的份额后计算得到x,然后各参与方分别计算Mi-xαi,对n个参与方的Mi-xαi求和,若求和的结果为0则验证通过. Keller等人[47]于2016年提出MASCOT,保持SPDZ的在线阶段不变,在预处理阶段使用COT生成Beaver三元组.Keller等人[81]于2018年提出方案KPD2018,使用BGV的加法同态代替原始方案中的FHE来生成Beaver三元组,获得了比MASCOT更好的性能. Cramer等人[82]于2018年提出了有限环上的方案SPDZ2K,环上的计算更接近于CPU计算单元的实际计算情况,有限环上的安全计算具备很高的实际意义,该方案的效率和有限域上的方案基本一致. 2.3.2 SS-MPC计算非线性运算 SS-MPC实现的非线性运算包括比较运算和最高有效位(most significant bit,MSB)运算. SecureNN实现的比较运算可以比较秘密值和常数值的大小,参与方拥有p上秘密值x的比特份额和明文比特串r,秘密值和常数值长度均为l位.从低位到高位依次为第1,2,…,l个比特计算比较运算时,对x和r的第i位从高位到低位依次计算由于r[i]-x[i]+1≥0,所以只要存在ci=0则说明同时满足和r[i]-x[i]=-1,即x和r的第i+1位至l位都相等且第i位x[i]>r[i],由此可得x>r;若不存在ci=0则x 表2对SS-MPC方案的安全模型和性能进行了对比.我们对乘法、比较(或最高有效位)运算的通信量和交互轮数2个方面进行比较,其中l为秘密比特串长度,p为有限域的大小.通过对比发现,ASTRA是半诚实安全模型下性能最好的方案,TRIDENT和BLAZE在恶意安全模型下实现的乘法运算具有较好的性能,但是在计算最高有效位时TRIDENT的性能更好.SecureNN的乘法性能为矩阵乘法运算的性能,其他方案是单个数据乘法运算的性能. Table 2 Comparison of SS-MPC Schemes表2 SS-MPC安全模型和性能比较 同态加密支持对多个数据的密文进行运算,解密得到的结果与数据明文运算结果一致.即明文与密文的运算满足同态性质: Dec(Enc(x+y))=Dec(Enc(x)⊕Enc(y)), 其中,+和⊕分别是明文和密文空间上的运算. 早在1978年Rivest等人就提出了隐私同态(privacy homomorphism)的概念,但这个概念一直被认为是一个开放性的问题,直到2009年Gentry提出首个全同态加密方案,证明了在加密数据上计算任何函数的可行性. 同态加密可以划分为部分同态加密(partial homomorphic encryption, PHE)、浅同态加密(somewhat homomorphic encryption, SHE)和全同态加密(fully homomorphic encryption, FHE).部分同态加密仅支持单一类型的密文同态运算,主要包括加法同态(additive homomorphic encryption, AHE)和乘法同态(multiplicative homomorphic encryption, MHE),代表方案分别为Paillier[83]和ElGamal[84].浅同态加密支持低次多项式运算.全同态加密的构造均遵循Gentry的思想蓝图,利用自举(bootstrapping)技术将浅同态加密方案转换为全同态加密方案,即通过同态地执行解密电路以更新密文、约减噪音,从而支持进一步的同态运算.目前主流的FHE方案大多基于格上的困难问题(主要是LWE,RLWE)构造,代表方案包括BGV[85],BFV[86-87],GSW[88],CGGI[89],CKKS[90]等. 基于(R)LWE构造的同态方案中,密钥切换(key switching)技术和模切换(modulus switching)技术分别用于解决同态乘法运算导致的密文维数和噪音量级增长问题.为了降低自举导致的性能开销,BGV方案利用密钥切换和模切换技术实现了一种不需要自举就能构造的层次全同态加密(leveled fully homomorphic encryption, leveled FHE)方案.层次全同态加密根据方案预期计算的电路深度设置参数,能够计算任意多项式深度的电路,已经可以满足多数应用场景下的计算需求.BFV方案中提出了一种新的张量技术,构造了一个标量不变的leveled FHE方案.GSW方案是基于近似特征向量法建立的简单全同态加密方案,消除了密钥切换过程,使得同态加法和乘法在很大程度上就是矩阵的加法和乘法.CGGI方案通过在环面上构造RGSW和RLWE的外部积,对加密比特进行门自举,在运行时间和可用性上具有优势.CKKS方案构造类似于BGV方案,支持定点数的近似运算. 根据明文空间的不同,同态加密方案可以进一步分为逐字同态加密(word-wise HE)和逐比特同态加密(bit-wise HE)两类.逐字运算的HE方案例如BGV,BFV和CKKS等,优点是支持打包技术,可以将多个明文打包为单个密文并以单指令多数据方式对明文进行操作,提高了运算效率;早期的逐字运算方案只支持加法及乘法等多项式计算,难以有效支持除法、根号等非多项式运算,2020年Cheon等人[91]提出通过复合多项式近似符号函数使用CKKS来实现同态比较.逐比特运算的HE方案包括TFHE,FHEW[92]等,优点是可以支持非多项式运算,但是由于不能使用打包技术导致性能显著低于逐字运算方案.阿里巴巴于2020年提出的全同态加密技术PEGASUS有效桥接逐字运算方案CKKS和逐比特运算方案FHEW两类全同态加密技术,使用CKKS密文有效计算线性函数,转换为FHEW密文形式后可通过查表来计算非线性运算. 单密钥同态方案只能对同一个密钥加密的密文进行运算,而多密钥全同态加密(Multikey-FHE, MKHE)支持对不同密钥加密的密文进行同态运算,但需要参与方联合解密密文.2012年首个NTRU型的MKHE方案提出[93],此后MKHE技术迅速发展,相继提出GSW型的MKHE[94-97]、BGV型的MKHE[98-99]和TFHE型的MKHE[100].MKHE方案的构造和实现上仍需进一步的优化,主要关注多跳功能(允许运算过程中有新的参与方加入)的实现、密钥(参与方)数量上限、密文增长、密钥切换优化等多个方面. 全同态加密可用于机器学习中的隐私保护并保持非交互性,比如PEGASUS[101]可以使用2种同态技术实现机器学习中的线性和非线性运算.文献[100]中数据拥有方和模型拥有方分别使用自己的公钥加密数据,并将其发送给服务器,服务器能够对2种密钥加密的密文进行运算. 本节对混淆电路、秘密分享和同态加密3类MPC基础技术的计算方数量、计算量、通信量和交互轮数进行分析对比,如表3所示: Table 3 Comparison of MPC Fundamental Schemes表3 不同MPC基础技术对比 GC-MPC由于实现了底层的基本逻辑运算符,因此具有通用性,可面向不同的应用逻辑.GC-MPC一般有2个计算方,若是基于BMR实现的协议则可以支持多个计算方.混淆电路的计算开销主要是对称加密或哈希函数的计算,计算开销较小;混淆电路交互轮数是恒定的2轮,通信量与电路门的数量成正比.GC-MPC在计算简单逻辑运算时具有优势,如比较运算和加法运算,但是在计算复杂运算时会产生庞大的电路从而导致通信量很大、性能降低.目前没有出现针对大数据量复杂计算的GC-MPC处理平台,GC-MPC只在一些小数据量、简单计算场景中有具体应用,比如拍卖、薪水公平性调研等. SS-MPC的计算方数量一般大于2,SS-MPC计算方的运算都是简单的加法和乘法运算,不涉及模幂运算,因此计算开销小.SS-MPC的轮数和电路深度成线性关系,导致计算方端到端通信会有较长时延.近年来随着算法优化和网络带宽不断提升,SS-MPC的性能优势不断凸显,逐渐成为目前应用最广的MPC技术.SS-MPC不仅能高效计算加法和乘法等线性运算,还能够计算比较大小、最高有效位和除法等非线性运算.目前SS-MPC的实际应用有Sharemind MPC等通用计算平台,以及CrypTFlow等PPML开源实现. HE-MPC通常支持两方运算,多密钥HE支持多方运算.HE-MPC的轮数恒定、通信量比前2种MPC技术小.但是HE-MPC的计算开销很大,其中同态加法和标量乘法(明文和同态密文相乘)计算开销相对较小,然而同态乘法无论是自举,还是leveled FHE都需要对密文进行降维和降噪从而产生大量计算开销.此外,一些HE方案密钥和密文空间复杂度高,需要较大的存储开销.对于一些具有深度较大的布尔或算术电路,同态加密计算效率难以被实际应用接受. 在实际应用中,计算函数一般是线性运算和非线性运算的组合,由于GC,SS和HE适用于不同场景,将多种MPC技术结合的混合技术能够获得更好的性能.表4中对现有MPC的实现进行总结. Table 4 The Implementations of MPC Schemes表4 MPC方案方现 机器学习广泛应用于计算机视觉、语音识别和自然语言处理等领域.图4为机器学习层次结构图,第1层为机器学习典型算法,第2层为机器学习组成模块,第3层为机器学习基本算子. Fig. 4 The hierarchy of machine learning图4 机器学习层次结构图 机器学习算法主要包括神经网络(neural networks, NN)、线性回归(linear regression)和逻辑回归(logistic regression)等.神经网络是机器学习应用最广泛的算法,由输入层、隐藏层和输出层构成,其中隐藏层包括卷积层(convolutional layer, CONV)、全连接层(fully connected layers, FC)和池化层(pooling layer).卷积层的运算是过滤器矩阵和数据特征向量的内积运算;全连接层的运算是先计算神经元向量与权重矩阵的内积再与偏移向量相加;池化层是计算过滤器窗口内元素的最大值或平均值,分别称为最大池化层和平均池化层.神经网络隐藏层和输出层都要使用激活函数(activation function)为神经元引入非线性因素,使得神经网络可以逼近任何非线性函数,隐藏层常用的激活函数有ReLU,Sigmoid和tanh.线性回归和逻辑回归算法相对简单,都可以看作是单层神经网络,其中逻辑回归使用了Sigmoid激活函数. 从机器学习底层的基本算子来看,卷积层、全连接层和平均池化层可以使用加法和乘法2种线性运算实现.最大池化层可以使用比较大小或最高有效位等非线性运算来实现.激活函数在PPML方案中通常被转换为线性运算和非线性运算的组合,例如将ReLU表示为ReLU(x)=max(0,x)=(MSB(x)⊕1)×x,文献[111]中提出可以使用多项式来近似激活函数Sigmoid(x)=1/(1+e-x): 将激活函数转换为加法、乘法和比较等基本算子组合函数的方法,可以更好地使用MPC来进行运算. 神经网络模型训练最常用的优化算法是梯度下降优化(gradient descent optimization)算法,包括正向传播和反向传播2个过程:正向传播是输入信息通过输入层经隐藏层逐层处理并传向输出层,然后对输出值计算损失函数;反向传播是依据微积分中的链式法则沿着输出层到输入层计算中间变量和参数的梯度,并更新参数;训练模型需要重复正向传播和反向传播多次直到模型收敛.神经网络推理的运算是一次正向传播的过程.在机器学习的计算过程中,用户数据和模型参数是浮点数的形式,而MPC只能对整数类型的数据做运算,因此在使用MPC完成PPML时,要将浮点数转换为固定点数(固定精度的整数),并且在计算乘法后要计算截断运算. 机器学习分为3种明文架构,在客户端-服务器架构中,客户端向服务器发送明文数据,服务器计算推理结果并返回给客户端.在外包计算架构中,数据拥有方(模型拥有方)将其数据(模型)发送给一组外包服务器,服务器得到运算结果后将其返回给数据拥有方.在联邦学习架构中,客户端在本地使用私有数据训练得到局部模型并将其上传到中央服务器,服务器聚合得到更新的模型. 针对明文的机器学习架构无法保证用户私有数据和服务商模型参数的隐私性,在明文架构中引入MPC技术能够实现隐私保护,得到3种基于MPC的PPML架构,分别为安全客户端-服务器架构(secure client server, S-CS)、安全外包计算(secure outsourced computation, S-OC)、安全联邦学习(secure federated learning, S-FL),如图5所示: Fig. 5 The construction of PPLM based MPC图5 基于MPC的PPML架构图 基于S-CS架构的PPML方案用于做神经网络推理,允许客户端在不向服务器透露其私有数据的情况下获得神经网络推理结果,同时保护服务器模型参数的隐私.该架构有时需要客户端和服务器协同计算,由于服务器拥有更强的算力,在设计算法时倾向于为服务器分配相对复杂的运算.与明文CS架构相比,S-CS架构中客户端通常需要参与运算. 基于S-OC架构的PPML方案支持神经网络的训练和推理.数据拥有方对私有数据计算份额后发送给一组不会合谋的服务器.在神经网络推理时,模型参数拥有方以秘密分享的方式将其机器学习模型托管到一组服务器上,客户端将私有数据秘密分享给这组服务器,每个服务器对私有数据份额、模型参数份额进行模型推理的协同计算,每个服务器将得到的推理结果份额返回给客户端,客户端对其进行秘密恢复后可得到完整的推理结果.在神经网络训练时,多个数据拥有方以秘密分享的方式将数据集托管到一组服务器上,服务器在联合数据集上训练机器学习模型.与明文OC架构不同,S-OC架构的计算服务器彼此之间不能合谋. 基于S-FL架构的PPML方案可以防止中央服务器执行模型逆向攻击(model inversion attack)来推测出用户的私有训练集,与明文FL架构不同,S-FL架构客户端在本地得到局部模型参数后,需要对其加密后再上传至中央服务器. 从MPC技术、性能和准确率3个方面对基于S-CS架构的PPML进行总结,如表5所示.表5中的方案都实现了多个基准工作的评估,本节选取部分评估实验来对比性能.其中Delphi和CrypTFlow2使用深度神经网络ResNet-32对CIFAR-100数据集进行推理,其余方案只在浅层神经网络实现了对MNIST数据集的推理. Table 5 The PPML Schemes based on S-CS Architecture表5 基于S-CS架构的PPML方案 从实现S-CS的MPC技术来看,CryptoNets,DeepSecure分别是基于单一技术HE和GC设计的方案,分别产生了较大的计算开销和通信开销.之后的PPML方案考虑线性层和非线性层的不同计算特性,组合多种MPC技术实现安全运算,对此类方案分析为: 1) S-CS架构的线性层实现.主要使用AHE和SS技术,标量乘法可以转换为AHE运算.MiniONN,GAZELLE和Delphi都使用AHE实现了线性层.GAZELLE与MiniONN相比,减少了同态运算次数、客户端和服务器的交互次数,并且设计了适用于机器学习的同态线性代数核.Delphi与GAZELLE相比,将在线阶段繁重的同态运算前移到预处理运算,降低了在线阶段的计算开销.Chameleon和CrypTFlow2分别使用SS,COT来实现线性层的运算.此外,DeepSecure和XONN都是应用于模型参数为二进制数的网络,因此使用GC来实现线性运算. 2) S-CS架构的非线性层实现.主要使用SS,GC和OT技术,使用SS来执行非线性层的运算.通常先对非线性运算进行多项式近似,然后再使用SS来执行运算,近似运算会导致准确率降低.使用GC来执行非线性层的运算虽然可以提高准确率,但是会增加通信开销,例如GAZELLE.CrypTFlow2使用OT来执行非线性运算,能够同时保证准确率和通信效率,获得了优于GC约7倍的通信效率.此外,也有一些方案为了同时获得可观的准确率和通信效率,分别使用GC和SS各完成一部分非线性运算,例如MiniONN,Chameleon和Delphi. 3) S-CS架构的MPC技术演进分析.通用神经网络(不包括BNN)线性层的实现只包含HE和SS技术,最早使用leveled FHE的方法来实现,其巨大的计算开销严重影响了方案的可用性.此后提出的AHE实现的优化包括算法层面的优化,即构造适用于S-CS场景的同态线性代数核;以及协议层面的优化,即将繁重的HE运算前移到预处理阶段,同时结合SS来完成线性运算,降低在线阶段的计算开销.通用神经网络非线性层技术是影响整个方案性能开销、准确率的关键,GC和SS分别只能满足高准确率和高性能,而无法同时达到最优效果.2020年提出的CrypTFlow2使用OT计算非线性运算,在保证准确率的前提下极大地提高了计算、通信效率. CryptoNets[112]是Microsoft提出的第一个使用同态加密实现隐私保护机器学习的方案,该方案的缺点是使用LHE友好的激活函数(例如平方函数)代替常用的ReLU和Sigmoid,影响了结果准确性,并且在牺牲准确性的前提下,计算成本依然非常大.CryptoNets每小时可完成59 000次推理. MiniONN[113]的线性层结合加性秘密分享和同态加密2种技术实现,客户端将私有数据拆分为2份并将其中一份发给服务器,服务器计算模型参数的同态密文并发给客户端,客户端对该密文和自己的数据份额计算乘法并将结果发给服务器,服务器结合这些信息可以计算出线性层的输出.对于非线性层,使用GC来计算激活函数ReLU,使用SS来计算激活函数Sigmoid和Tanh的多项式近似函数. Chameleon[114]的线性层使用秘密分享方案Beaver三元组来计算,引入可信第三方在离线阶段生成相关随机数.非线性层使用GMW或GC计算,由于GMW的轮数和电路深度有关,因此当电路深度较深时使用GC计算非线性层,其余情况使用GMW计算非线性层.Chameleon的运行时间比MiniONN快4.2倍. GAZELLE方案[115]设计了同态线性代数核来优化同态运算,并使用优化的AHE方案计算线性层,使用GC来计算ReLU所需的比较运算,并通过加性秘密分享技术在LHE和GC之间有效切换.计算线性层时,客户端计算输入数据x的密文Enc(x)并发送给服务器,服务器对Enc(x)和自己拥有的模型明文参数计算标量乘法得到线性层输出的密文Enc(y).由于密文Enc(y)不能直接作为GC的输入,并且如果将Enc(y)发给客户端解密可能会泄露模型参数.使用秘密分享可以解决这个问题:服务器选取随机数作为份额-ys,并计算Enc(y)+Enc(ys)=Enc(y+ys)发送给客户端,客户端解密获得份额yc=y+ys,将yc和-ys作为GC的输入便能计算非线性函数.GAZELLE方案在线阶段的运行时间比Chameleon快20倍. Delphi[116]将GAZELLE线性层繁重的同态加密运算前移到预处理阶段,客户端私有数据为x,服务器拥有模型参数M.在线性层的预处理阶段,客户端选取随机数r,对其计算同态密文Enc(r)并发给服务器;服务器选取随机数s作为线性层份额并计 算Enc(Mr-s)并发给客户端;客户端解密得到Mr-s并将其作为线性层份额.在线性层的在线阶段,客户端计算x-r并发送给服务器,服务器设置线性层份额为M(x-r)+s,可见双方的份额之和等于线性计算结果Mx.对非线性层的改进是使用多项式近似激活函数并用Beaver三元组来计算,这种方法在减小开销的同时也会导致准确率降低,考虑到效率和准确率的折中,在保证准确率满足阈值的前提下最大化近似计算激活函数的数量,并分别使用GC和SS计算2部分激活函数.Delphi获得的准确率与明文模型准确率相差不到0.04%,运行时间比GAZELLE快22倍、通信效率提升9倍. 先前工作在实现ReLU时存在通信开销大或准确率低等问题,CrypTFlow2使用OT实现的比较大小运算避免了先前方案的弊端.参与方P0,P1在比较长度为l位的私有数据x和y时,可以将其拆分为高位、低位比特串的拼接x=x1‖x0,y=y1‖y0,使用式1{x DeepSecure[117]和XONN适用于二进制神经网络的安全推理.DeepSecure对GC组件进行优化并引入了降低开销的预处理技术,运行时间优于CryptoNets,但同时也带来了更大的通信开销.XONN[118]将神经网络中线性层的运算转换为向量点乘运算,神经网络第一层客户端输入数据是整数、神经网络权重是二进制,使用OT计算整数和二进制数的向量点乘;神经网络中间层运算数据都是二进制值0和1,使用同或(XNOR)和加法来计算二进制点乘运算,由于可用XOR代替XNOR运算,且GC已经实现Free-XOR,因此整个方案的开销较小,性能优于GAZELLE方案7倍. 从参与方数量、机器学习功能、安全模型和MPC技术等方面对现有基于S-OC架构的PPML方案进行总结,如表6所示: Table 6 The PPLM Schemes Based on S-OC Architecture表6 基于S-OC架构的PPML方案 1) S-OC架构的MPC技术.基于S-OC架构的方案主要使用秘密分享技术,通常需要2~4个计算方协同计算.ABY3等方案通过设置冗余的加性秘密份额实现了门限的效果,可以容忍一个参与方的单点失效,增强了系统的容错能力,其中ABY3实现了中止安全性,ASTRA等实现了安全性更强的公平性. 2) S-OC架构的安全模型.部分方案只设计了单一安全模型下的方案,例如半诚实安全模型下的SecureML、恶意安全模型下的BLAZE,还有一些方案分别构造了半诚实和恶意2种安全模型下的方案,例如ASTRA等. 3) S-OC架构支持的机器学习功能.表6中所有方案都能支持神经网络推理,除ASTRA和CrypTFlow以外其他方案都能支持神经网络训练. 4) S-OC架构与S-CS架构的对比.S-CS架构中应用了多种MPC技术,包括AHE,OT,GC,SS等.而在S-OC架构中主要使用单一的SS技术,因为机器学习在训练模型时需要迭代计算多次,SS是计算开销最小的MPC技术,能够有效降低模型训练时间.现有的HE和OT方案无法有效支持S-OC架构下的安全多方计算. SecureML是半诚实安全模型下的两方计算方案.整个训练过程分为离线和在线2个阶段,离线阶段利用HE或者OT生成Beaver三元组;在线阶段计算线性层运算时使用秘密分享技术,计算激活函数时使用平方函数做近似并通过GC来计算,然而近似运算导致精度降低,只获得了93.4%的准确率. 与SecureML结构类似,QUOTIENT[119]也是半诚实安全模型下的两方计算方案.该方案将模型参数表示为三元值{-1,0,1}、私有数据表示为整数形式,因此计算方需要对算术份额和布尔份额进行运算,使用COT来完成乘法运算,使用GC来完成非线性运算.QUOTIENT的模型推理采用S-CS架构,而其他S-OC方案的模型推理依然是外包给计算方来完成.QUOTIENT对ResNet32模型进行训练,准确率与明文模型相比只降低了0.1%~2.17%,与SecureML相比运行效率提高了13倍. ABY3是首个三方计算场景下的混合协议,由算术秘密分享、布尔秘密分享和姚氏电路3种MPC技术构成.三方的设置无法使用传统的两方混淆电路方案,只能使用专门为三方设计的混淆电路.该方案还设计了不同MPC技术的高效切换协议.ABY3使用MNIST数据集训练得到的模型准确性为93%~99%,神经网络、线性回归的训练时间比SecureML快80~55 000倍. ASTRA对ABY3线性计算的改进是将一部分在线阶段的运算前移到预处理阶段,对非线性运算的改进是使用秘密分享代替并行前缀加法器,获得了恒定轮数的效果.ASTRA只实现了线性回归、逻辑回归等模型的安全推理,而未实现模型训练.BLAZE与ASTRA相比的改进是提供对神经网络模型的支持,并且增加模型训练的功能.TRIDENT在ABY3的基础上,将线性层的截断计算和乘法计算合并来避免额外的通信开销,并且优化了ASTRA的最高有效位计算方法. SecureNN仅使用秘密分享技术构造了神经网络中的线性层和非线性层,四方设置比三方设置获得更好的性能,其对MNIIST数据集进行模型训练和推理,获得93.4%~99.15%的准确率,比明文模型训练开销增加17~33倍. SecureNN等方案在实现时都需要手动在MPC友好的低级语言或开发库上实现PPML模型,这种方式对ML开发者不够友好.CrypTFlow[120]编译器能够自动将TensorFlow的推理代码转换为多种MPC协议,在实现编译器后端MPC协议时对SecureNN三方计算方案的通信效率进行改进,更便于开发者使用.SecureNN将矩阵x和y的卷积计算转换为更大的矩阵x′和y′的乘法,然后使用Beaver三元组来计算x′和y′的积来获得卷积结果,其中变形矩阵x′有冗余参数会增大通信开销.CrypTFlow的改进是先使用Beaver三元组计算原始矩阵x和y的积,得到中间结果的份额后,参与方在本地对矩阵进行转换,避免交互过程中传输冗余的信息.CrypTFlow对SecureNN非线性层的改进是消除辅助节点向2个计算方发送份额的过程,将ReLU和最大池化层的通信开销降低了1/4.最后,CrypTFlow使用SGX技术将MPC协议从半诚实安全转换为恶意安全.CrypTFlow目前只实现了神经网络推理,准确性与明文推理相近,半诚实安全方案和恶意安全方案的运行时间分别为30 s和2 min. 此外,国内提出的方案PrivPy[121]由语言前端和计算引擎后端组成,前端提供编程接口和代码优化,后端执行基于秘密分享的隐私保护计算.PrivPy支持3种后端:PrivPy设计的2-out-of-4秘密分享协议后端、SPDZ和ABY3.PrivPy设计的后端需要采用二次秘密分享技术,前2个参与方获得私有数据份额后,再计算新的份额发送给后2个计算方,通过冗余份额的设置,在秘密恢复阶段只要有2个参与方即可恢复出计算结果.PrivPy实现的模型训练和推理的性能均优于ABY3. 联邦学习(FL)是为了解决数据孤岛问题而提出的机器学习算法,由一个中央服务器和多个客户端组成.客户端在本地使用私有数据训练模型,将模型梯度发送至中央服务器.服务器整合多个客户端的模型梯度得到全局模型.FL架构仅需要传输模型梯度,客户端的私有数据自始至终没有离开本地,即便如此,研究表明中央服务器可以通过对模型逆向攻击来推测出客户端数据. 为了保护用户数据隐私,Shokri等人[122]于2015年提出的方案在模型准确性和隐私保护之间进行折中,提出将模型梯度的1%~10%上传到云服务器的方法.Aono等人[123]于2017年证明攻击者从部分梯度中也能推测出有用信息,并使用密码学来解决隐私泄露的问题:客户端在本地使用加法同态算法对局部模型梯度加密并将密文上传至中央服务器,服务器对各参与方的密文计算同态加法并将结果返回给客户端,客户端解密后得到更新的模型梯度.谷歌[124]于2017年提出了基于秘密分享实现的联邦学习安全聚合方案,参与方使用秘密分享计算掩码向量,使用掩码向量对局部梯度计算异或加密并上传至服务器.服务器先对收到的数据求和,然后使用秘密恢复技术计算出掩码向量,并将其从求和值中消去,得到全局模型.该方案利用Shamir的门限特性,只要用户数量满足门限就消去掩码,解决了实际应用中可能存在的用户中途退出问题.谷歌将该方案应用于GBoard输入法中来进行单词预测. 目前已有一些基于MPC实现的联邦学习框架投入使用.FATE项目最初使用加法同态加密技术来构建联邦学习底层安全计算协议,在之后的版本上增加了SPDZ秘密分享协议,提供更多样化的MPC协议支持.此外,2019年发布的PySyft是用于隐私保护深度学习的开源库,将SPDZ等MPC技术和差分隐私集成到联邦学习框架并向用户提供应用程序接口. 安全多方计算提出的前20年一直停留在理论层面的研究,没有应用于实际生活中的方案和系统.2000年以来,各种MPC基础技术在实践中都有了相应的系统实现,例如Fairplay,Sharemind MPC和SEAL等.在大数据应用的推动下,MPC基础理论的迭代更新和工程实践的广泛应用体现了其学术和实用价值,MPC在未来的发展中有巨大的潜力和广阔的发展前景. PPML是当前最受关注的MPC应用领域,近年来在可用性和准确性等方面取得了很大的进步,但是仍然有许多问题需要解决,未来工作可围绕以下3个方面展开. 1) 进一步提升准确率与系统性能.MPC实现的PPML方案开销依然远大于明文模型的运算,准确率与明文模型相比还是会有一定的损失.PPML方案非线性层的实现方式会为准确率带来很大的影响,相对而言GC精度较高但性能开销大,SS性能较好但无法达到GC的精度,现有PPML方案都在效率和准确率之间进行折中.最新提出的使用OT实现非线性运算的方案同时获得了性能和准确率的保证,仅适用于两方参与的场景.因此MPC基础技术的优化将对PPML技术的性能优化起到重要作用.此外,在PPML使用混合技术方案中降低不同技术的转换开销也将进一步提升PPML技术的可用性. 2) 提升系统安全性.现有的很多方案都只满足半诚实安全模型,未来需要进一步加强对恶意敌手的防御.另一方面,早期的恶意安全方案实现了中止安全性,2019年之后的方案都达到了更强的安全属性-公平性,提升系统的安全属性也是今后研究的一个重要方向,未来要实现的安全目标是能够保证结果输出(GOD),并且在性能开销也需要控制在可接受范围内. 3) 降低模型隐私泄露风险.现有的部分S-CS架构下的方案会向客户端泄露过滤器的大小、卷积的步长以及神经网络隐藏层的种类等模型信息.未来仍需进一步探索对模型参数信息更有效的保护方案.2 MPC技术发展
2.1 混淆电路


2.2 不经意传输


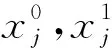

2.3 秘密分享
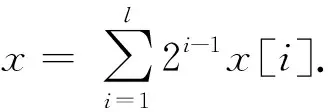


2.4 同态加密
3 MPC基础技术的比较
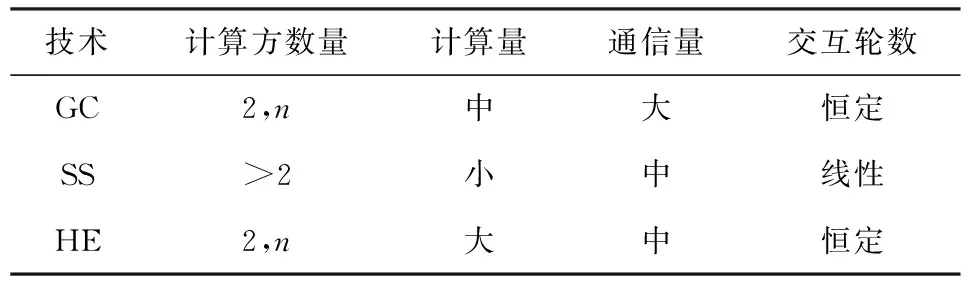
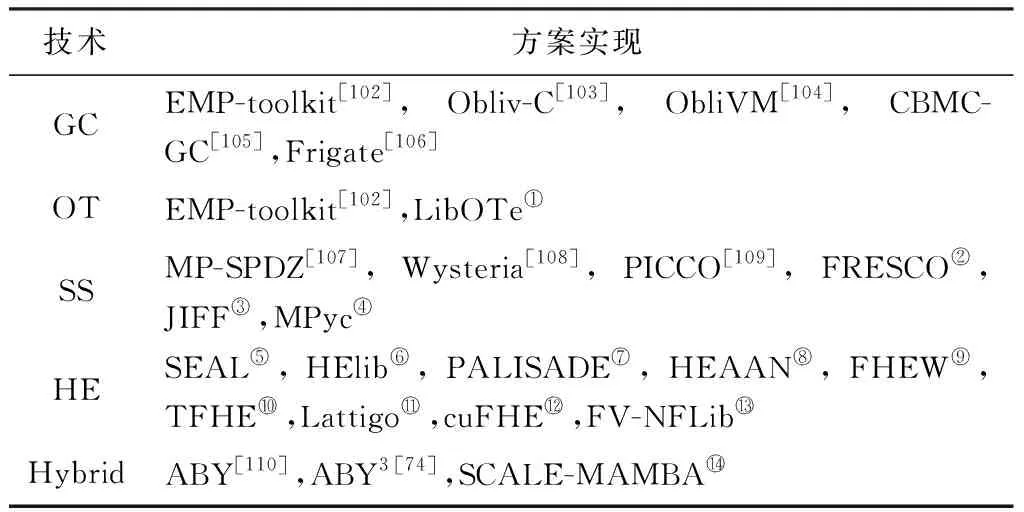
4 隐私保护机器学习
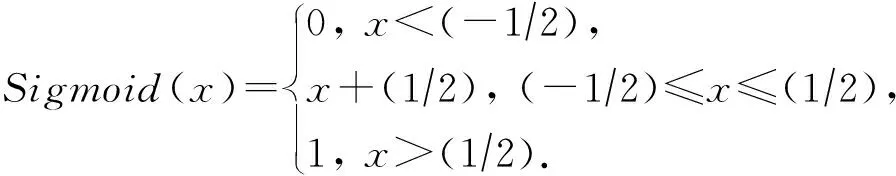
4.1 基于S-CS架构的PPML
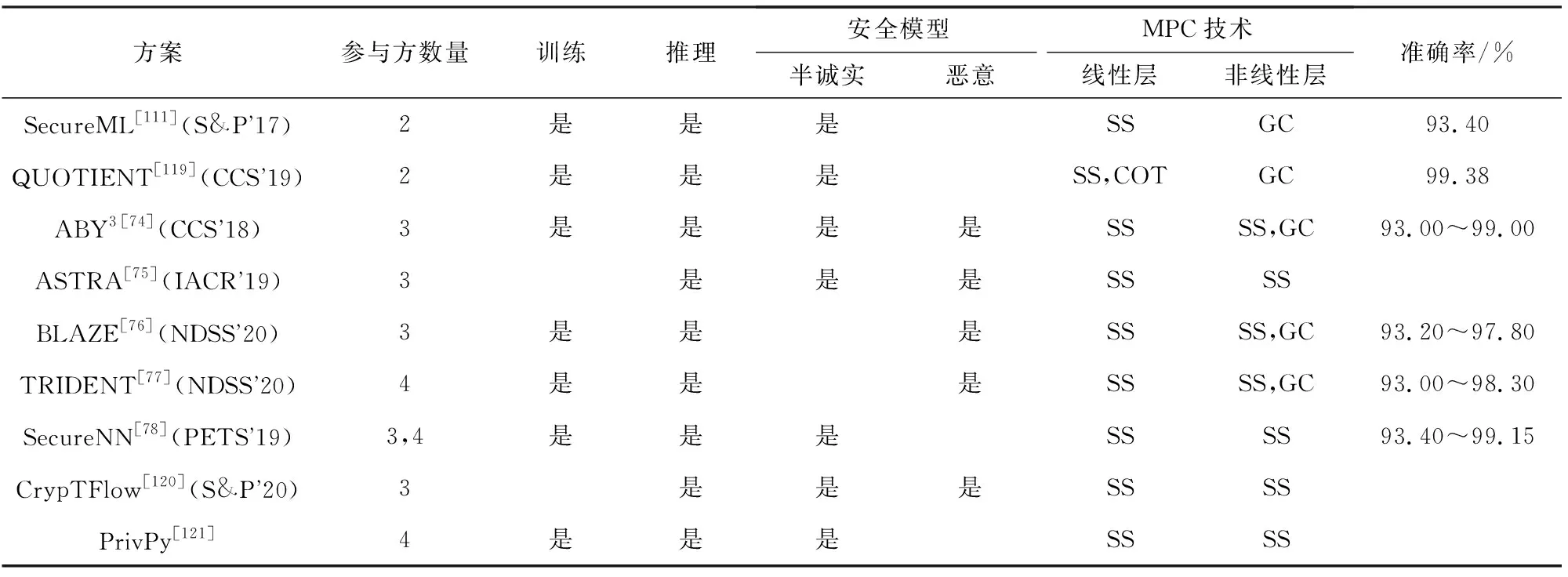
4.2 基于S-OC架构的PPML
4.3 基于S-FL架构的PPML
5 总结与展望

