标准模型下的灵活细粒度授权密文一致性检测方案

邓翔天 钱海峰

(华东师范大学软件工程学院 上海 200062)

密文一致性检测公钥加密方案(public key encryption with equality test, PKEET)最初由Yang等人提出[1]，其允许用户在不持有对应私钥的情况下检测一组密文解密所得明文的一致性，受检测的密文对加密时所用的公钥不必相同.

然而，Yang等人提出的PKEET方案允许任意用户对密文进行一致性检测.为了避免这一特性带来的安全风险，Tang[2]提出了全有或全无密文一致性检测方案(all-or-nothing PKEET, AoN-PKEET，在该方案中，私钥持有者通过选择性地发放由私钥生成的令牌，自主授权“代理”执行密文一致性检测操作.令牌机制在隐私保护方面起到关键作用，因而被大量相关工作借鉴沿用[2-7](1)多项已有工作将AoN-PKEET方案视作一种特殊的PKEET方案，并直接称呼其为PKEET方案，本文将沿用这一做法..

后续工作中，细粒度授权密文一致性检测公钥加密方案(fine-grained PKEET, FG-PKEET)[3]允许一对用户通过交互生成令牌并将其发送至代理.该令牌只可被用于检测2个用户公钥加密所得任意密文的一致性.

由Ma等人[4]提出的灵活授权密文一致性检测公钥加密方案(PKEET with flexible authorization, PKEET-FA)则将授权客体从用户层次扩展至密文层次：其在PKEET方案的基础上添加多类令牌，分别用于检测2个指定密文的一致性，即密文-密文级别令牌，或是检测一指定密文和另一指定用户的任意密文的一致性，即密文-用户级别令牌.

到目前为止，相关工作中提及的FG-PKEET，PKEET-FA方案在功能性方面互不包含，并且拥有各自适用的应用场景.FG-PKEET方案的授权客体类型局限于用户类型.同时，以具体的PKEET-FA方案[4]为例，尽管该方案中，密文-密文级别、密文-用户级别的令牌的授权客体可以为指定某一密文，但是该方案未能实现FG-PKEET方案中的令牌功能，即能够检测指定2位特定用户的任意密文一致性的用户-用户级别令牌.此外，目前提出的FG-PKEET，PKEET-FA方案的安全性证明均建立于随机预言机模型之上，需要在安全证明中设立随机预言机扮演方案中的Hash函数.

针对现状，我们的FG-PKEET方案具备2个创新点：

1) 我们所提出的FG-PKEET方案在功能性上兼顾了FG-PKEET方案与PKEET-FA方案的特性，拥有更细的令牌授权粒度，并且具备对应的安全性质.

2) 在实际应用场景中，使用具体的Hash函数来代替随机预言机存在安全隐患[8].我们所提出方案的安全性则建立于标准模型之上，在安全性方面更加可靠.

1 预备知识

本节我们将对文中所用符号与密码学原语的定义进行简要解释；汇总并介绍相关工作成果；对本方案安全性质所依赖的密码学假设进行介绍.

1.1 符号定义与密码学原语介绍

1) 符号定义

对于一个有限集合S，我们使用公式s←rS来指代从有限集合S中均匀随机采样得一个随机元素S这一过程.

我们声称函数f关于λ是可忽略的，当且仅当不等式f(λ)≤1/p(λ)对于所有的多项式p(·)和足够大的λ成立.

2) Hash函数

在我们所提出的方案中使用的Hash函数，应具备2个性质：

关于λ是可忽略的.

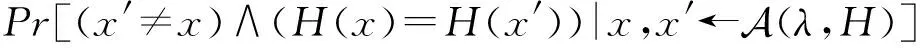
关于λ是可忽略的.

3) 双线性映射

令q是一个素数，G1和G2是2个阶为q的群，G1到G2的双线性映射e:G1×G2→GT应满足3个性质：

① 双线性.对任意P,Q∈G1,R,S∈G2和a,b∈q，满足e(aP,bR)=e(P,R)ab,e(PQ,R)=e(P,R)×e(Q,R)和e(P,RS)=e(P,R)×e(P,S).

② 非退化性.映射不会把G1×G2中的任何元素映射到GT中的单位元.

③ 可计算性.对于任意的P∈G1,Q∈G2，存在一个有效算法计算e(P,Q).

同时，双线性映射可根据G1,G2所具备的性质进一步分类[9]，在一类双线性映射中G1=G2；在3类双线性映射中，G1≠G2且G1,G2间不存在可高效计算的同构关系.

1.2 相关工作介绍

FG-PKEET方案由Tang首次提出[3].在FG-PKEET方案中，一对用户需进行交互以生成令牌.该令牌只可被用于检测该2名用户的公钥加密所得密文的一致性.与PKEET方案相比较，FG-PKEET方案之中用户需消耗更多的时间消耗令牌，但是能够获得更细粒度的授权机制.

PKEET-FA方案由Ma等人首次提出[4].在该方案中，授权客体类别包括用户类和密文类.

以Ma的具体方案为例，它总共包含4类令牌：1)一类令牌，用户级别令牌，其定义与PKEET方案中令牌的定义一致；2)二类令牌，密文级别令牌，如果一名代理接收到2个密文对应的二类令牌，那么他能够检测该2个密文的一致性；3)三类令牌，密文-密文级别令牌，其授权客体为2个指定密文，即该令牌只能够被用于检测这2个指定密文的一致性；4)四类令牌，密文-用户级别令牌，该令牌的授权客体是一个密文和一名用户.接收到该令牌的代理能够使用其检测指定密文和指定用户公钥加密所得的密文的一致性.

在安全性方面，文献[10]指出在标准模型下设计可证明安全的密码学方案是一项重要的研究课题.近来，已有多种具备标准模型安全性的PKEET方案被提出.其中Zhang等人[5]提出的方案基于特定的数论假设，其在具体设计思路上借鉴了由Lai等人提出的公钥加密方案[11]；其余2种PKEET方案分别由Lee等人提出[6]和Zeng等人[7]提出，前者在设计方案中使用了密码学原语基于身份加密方案(identity-based encryption, IBE)和一次性签名方案(one-time signature scheme)，而后者使用Hash证明系统(Hash proof system, HPS)，因此这2种方案均为可灵活选择所依赖的具体数论假设的通用方案.

1.3 数论假设介绍

1) 判定性双线性Diffie-Hellman(decisional bilinear Diffie-Hellman, DBDH)假设

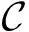
G,GT上的DBDH假设声称对于任意PPT敌手，其在上述游戏中的优势对于安全参数λ是可忽略的.

2) 外部判定性Diffie-Hellman(external decisional bilinear Diffie-Hellman, Ex-DDH)假设

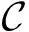
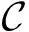
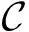
G1,G2,GT上的Ex-DDH假设声称对于任意PPT敌手，其在游戏中的优势对于安全参数λ是可忽略的.

3) 外部判定性双线性Diffie-Hellman假设(external decisional bilinear Diffie-Hellman assumption, Ex-DBDH)

该假设在FG-PKEET方案[3]中首次被提出，并被用于方案安全性的归约证明.

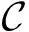
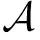
G1,G2,GT上的Ex-DBDH假设声称对于任意PPT敌手，其在上述游戏中的优势对于安全参数λ是可忽略的.

2 细粒度密文一致性检测方案定义

本节我们将对所设计的细粒度密文一致性检测方案进行介绍，包括方案模型定义、合理性定义、方案安全模型定义以及方案安全性质定义.

本节会提及多个特定用户的密文元组/密钥对，本文将使用下标区分它们.

2.1 方案模型定义及合理性定义

1) 方案各函数定义

KeyGen(λ):该非确定性算法接收一个安全参数作为输入，输出公私钥对(PK,SK).

Enc(m,PK):该非确定性算法接收一个取自消息空间M的明文消息m以及一个公钥作为输入，输出密文C.

Dec(C,SK):该确定性算法接收一个密文、一个私钥作为输入，其输出解密所得的消息m，或输出⊥表示解密失败.

Aut(SKi,SKj):该非确定性算法需要用户Ui,Uj以及一名代理交互执行.2名用户使用他们各自的私钥作为输入、输出令牌Ti,j.

Com(Ci,Cj,Ti,j):该确定性算法接收由用户公钥PKi,PKj分别加密所得的密文Ci,Cj和对应的令牌Ti,j作为输入.该算法输出⊥表示拒绝验证，如果Ci,Cj解密后对应的明文Mi,Mj相同则输出1，否则输出0.

Aut1(SKi,Ci,SKj):该非确定性算法需要Ui,Uj以及一名代理交互执行，使用Ui,Uj各自的私钥作为输入，此外，其中一名用户将其公钥加密得到的密文作为输入，在此不妨令该密文为使用Ui的公钥PKi加密得到的Ci，该算法输出令牌Ti,j,Ci作为结果，或者输出⊥表示拒绝生成.

Com1(Ci,Ti,j,Ci,Cj):该确定性算法接收一类令牌Ti,j,Ci和另一用户Uj公钥加密所得密文Cj作为输入.该算法输出⊥表示拒绝验证，如果Ci,Cj解密后对应的明文Mi,Mj相同则输出1，否则输出0.

Aut2(SKi,Ci,SKj,Cj):该非确定性算法需要Ui,Uj以及一名代理交互执行，使用2名用户各自的私钥和各自公钥加密所得的密文作为输入，输出二类令牌Ti,j,Ci,Cj，或⊥表示拒绝生成.由于代理可直接通过接收到的令牌检测Ci,Cj的一致性，因此不给出Com2的定义.

2) 方案合理性(Soundness)定义

细粒度密文一致性检测方案具备合理性，当且仅当加解密正确性、一致性检测正确性这2个性质对任意2名用户，和任意一对明文m,m′∈M成立.令用户为Ut,Uw，对应的公私钥对为(pkt,skt),(pkw,skw).

加解密正确性表达式定义为

Dec(Enc(m,pkt),skt)=m,Dec(Enc(m′,pkw),skw)=m′.

一致性检测正确性的具体表述为：

当m=m′时，Com算法的输出必定为1.反之，Com输出1的概率是可忽略的.

Com(Enc(m,pkt),Enc(m′,pkw),Aut(skt,skw)).

当m=m′时，Com1算法的输出必定为1.反之，Com1输出1的概率是可忽略的.

Com1(Enc(m′,pkw),Aut1(skt,skw,Enc(m,pkt))).

接收Aut2算法执行生成的令牌后，当m=m′时，代理必定判定2组密文代理必定判定2组密文经对应私钥解密所得的明文是相同的，即这对密文具备一致性.反之，代理误判一致性的概率是可忽略的.

Aut2(SKt,Enc(m,pkt),SKw,Enc(m′,pkw)).

2.2 方案安全模型定义

首先，为了简化模型，我们需对模型中各类用户的行为进行假设:

1) 所有用户诚实地生成他们的公私钥对，执行Aut,Aut1,Aut2算法，并且Aut,Aut1,Aut2算法的交互过程是在可信信道中完成的.

2) 代理是半诚信的，并且能够被授权检测多对用户的密文的一致性.

3) 普通用户集合与代理集合不存在交集.

PKEET的功能性使得基于不可区分的安全性质能够被拥有特定令牌的敌手轻易攻破.为此我们参考Tang提出的建模方法[3]，将敌手分为2类：

1) 一类敌手.该类敌手为半诚信的，经Ut,Uw授权的代理.

2) 二类敌手.该类敌手指代的潜在敌手包括除Ut,Uw以外的普通用户，以及未被Ut授权的代理.

对于不同种类的敌手，灵活细粒度密文一致性检测方案能够保证相应级别的安全性质，在此不妨令受攻击的用户为Ut,Uw：

针对一类敌手，灵活细粒度密文一致性检测方案应满足2个性质：

1) 适应性选择密文攻击下的密文单向性(one-wayness adaptive chosen ciphertext attack, OW-CCA2).OW-CCA2安全性保证一名敌手无法从挑战密文中恢复对应明文，即使他能够在特定限制下访问解密预言机.

2) 细粒度授权性(fine-grained authorization, FG-Auth).如果2名用户没有授权一名代理对他们的密文进行一致性检测，FG-Auth性质保证该代理无法越权检测2名用户密文的一致性.

针对二类敌手，细粒度一致性检测方案应满足性质为：

适应性选择密文攻击下的密文不可区分性(indistinguishability adaptive chosen ciphertext attack, IND-CCA2).IND-CCA2性质保证敌手无法从挑战密文中恢复明文，即使他能够指定一对明文并要求挑战者只能选择其中一个生成挑战密文.CCA2性质允许敌手带有限制地访问解密预言机，同时，根据对于二类敌手的定义，其能够以普通用户的身份参与令牌的生成过程.

2.3 安全性质定义

为便于后文描述，我们将查询阶段中序号为i的Dec请求称为关于用户Ui的解密请求.

OW-CCA2游戏的具体定义为：

1) 初始化.敌手声明一个序号t∈[1,N]作为其攻击对象.挑战者执行KeyGen函数，生成若干生成公私钥对(PKi,SKi)，其中1≤i≤N.

2) 查询阶段-1.在该阶段中敌手被允许向挑战者提交3个请求：

①Dec.提交密文C和序号i作为输入，挑战者返回Dec(C,SKi)

②Aut.提交2个序号i,j作为输入，挑战者执行Aut算法，敌手在算法中扮演“代理”角色.

③Aut1,Aut2.提交序号i,j和密文ci(密文ci,cj)作为输入，挑战者执行Aut1,Aut2算法，敌手在算法中扮演“代理”角色.

5) 敌手输出他对于挑战消息的猜测,游戏结束.

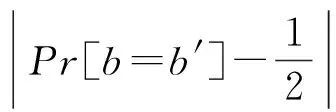
FG-Auth游戏的具体定义为：

1) 初始化.敌手声明2个不同的序号t,w∈[1,N]作为其攻击对象.挑战者执行KeyGen函数，为1≤i≤N生成公私钥对(PKi,SKi).

2) 查询阶段-1.在该阶段中敌手被允许向挑战者提交3个请求：

①Dec.提交密文C和序号i作为输入，挑战者返回Dec(C,SKi).

②Aut.提交2个序号i,j作为输入，挑战者执行Aut算法，敌手在算法中扮演“代理”角色.限制是i,j不能同时为t,w.

③Aut1,Aut2.提交序号i,j和密文Ci(密文Ci,密文Cj)作为输入，挑战者执行Aut1,Aut2算法，敌手在算法中扮演“代理”角色.

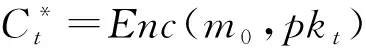
5) 敌手输出他对于挑战消息的猜测b′，游戏结束.

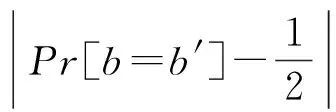
IND-CCA2游戏的具体定义为：

1) 初始化.敌手声明特定序号t∈[1,n]作为其攻击对象.挑战者执行KeyGen函数，为1≤i≤N生成公私钥对(PKi,SKi).

2) 查询阶段-1.在该阶段中敌手被允许向挑战者提交4个请求：

①KeyRetrieve.提交序号i作为输入，挑战者返回SKi，敌手不可使用t作为参数.

②Dec.提交密文C和序号i作为输入，挑战者返回Dec(C,SKi).

③Aut.提交2个序号t,j作为输入，其中j≠t，挑战者执行Aut算法，敌手在算法中扮演Uj角色.

④Aut1(Aut2).提交序号t,j和密文c1(密文c1,c2)作为输入，其中j≠t.挑战者执行Aut1(Aut2)算法，敌手在算法中扮演Uj角色.

敌手选择2个消息m0,m1并发送至挑战者，进入下一阶段.

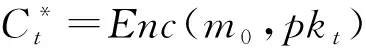
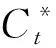
5) 敌手输出他对于挑战消息的猜测b′，游戏结束.

3 细粒度密文一致性检测方案构造

3.1 细粒度密文一致性检测方案描述

1) 公共参数定义

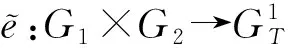
2) 函数定义

KeyGen(λ)：该算法随机选取α,x,y,z∈p,g2∈G,θ∈q，并赋值g1=gα,u=gx,v=gy,d=gz.最终生成的公钥元组为(Z=e(g1,g2),u,v,d,)，私钥元组为(,x,y,z,θ).

Enc(m,pk)→(C0,C1,C2,C3,C4,C5)：该算法需执行运算：

s,r←rC1=gs;C2=(utvrd)s;t=H1(C0‖C1‖C3‖C4).

在加密算法和解密算法中，我们需要一个公共的编码/解码函数，其在二元组m,ω与GT间映射.为简洁起见，我们在后面的公式中省略“encode”,“decode”下标.该公共函数使得|p|,|q|间存在隐含关系：令消息明文空间为q，那么不等式|q|2≤|p|必须成立.

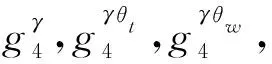
① 用户Ut,Uw各自随机选取γt,γw←r并将发送给彼此.

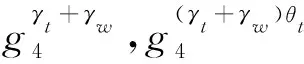
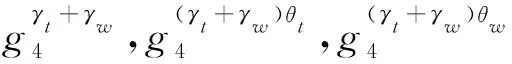
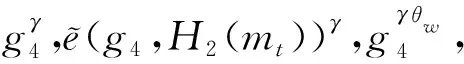
具体过程为：

① 用户Ut,Uw各自随机选取γt,γw←r分别将和发送至对方.

② 用户Ut使用私钥解密Ct，如果解密结果为⊥，那么整个过程中止并输出⊥.这一解密行为可视作对密文Ct的校验操作，输出⊥表示校验失败，反之则校验成功.

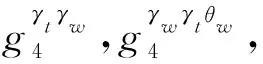
④ 代理令算法Aut1(Ct,skt,skw)产生的令牌(tkr,tkt,tkw)为

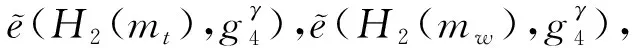
具体过程为：

① 用户Ut使用私钥解密Ct，如果解密结果为⊥，那么整个过程中止并输出⊥，用户Uw执行类似的步骤.解密行为可对应视作为对密文Ct,Cw的校验操作，输出⊥表示校验失败，反之则校验成功.

②Uw随机选择γw←r并发送至Ut；Ut随机选取γt←并发送至Uw.

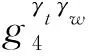
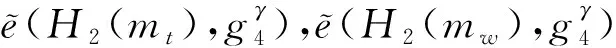
显然，代理可通过判断tkt与tkw是否相等以检测对应密文的一致性.过程步骤②中用户间传递的值被称为Aut2中产生的中间值.

Com(Ct,Cw,tokent,w)作为参数所提交的密文，代理计算t=H1(C0,C1,C3,C4)，并判断等式e(C1,g)=e(utvC5w,C2)是否成立，如果不成立，则输出⊥并中止.该算法的输出结果：

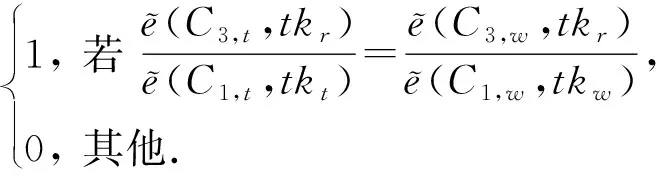
Com1(Cw,tokent,w,Ct)作为参数所提交的密文，代理计算使用Com中述及的方法对密文进行校验，如果不成立，则输出⊥并中止.该算法的输出结果：

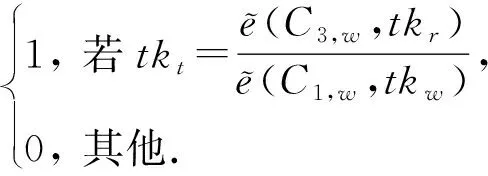
3.2 细粒度密文一致性检测方案合理性证明

1) 加解密正确性

以用户Ut的私钥skt和使用pkt诚实生成的密文C为例，正确性证明的推导为

等式对应提取明文信息m与组件ω一步.

该等式对应从C4中提取Hash值一步.

2) 一致性检测正确性

在算法Com中，给定2个诚实生成的密文Ct,Cw和相应的令牌，Ct,tkt,tkr对应的计算过程为

将Cw,tkw,tkr带入式中，在mt=mw的情况下，将得到相同的结果，因此算法必定能够判定2组密文保持一致性.反之，当且仅当发生Hash碰撞时，该函数会输出错误判断.根据前文中Hash函数的定义，该事件的发生概率是可忽略的.

对于Com1算法以及Aut2算法的一致性检测正确性证明与该证明过程类似，故此省略.

4 细粒度密文一致性检测方案安全性证明

4.1 IND-CCA2安全性

定理1.在G1上的XDH假设、G上的DBDH假设成立的前提下，3.1节构造的FG-PKEET方案在标准模型下具备针对二类敌手的IND-CCA2安全性.

证明. 为证明该方案具备相关安全性质，可以第2节中定义的IND-CCA2游戏为基础，构建一系列游戏，最终使敌手在最后一个游戏中的优势是可忽略的，且敌手无法将其与原游戏区分.

游戏0. 与定义3中的IND-CCA2游戏描述一致.

游戏1.挑战者对挑战密文进行改动:

我们将通过引理1，证明当DBDH假设成立时，PPT敌手区分游戏0和游戏1的概率是可忽略的.

引理1.如果G上的DBDH假设成立，则以不可忽略概率区分Game0,Game1的PPT敌手不存在.

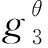
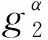
2) 查询阶段-1.

e(C1,utvrd)=e(g,C2).

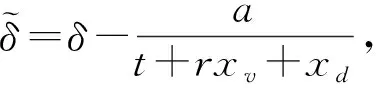
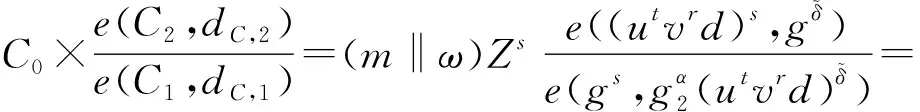
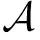
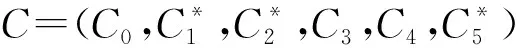
(m*‖ω*)T=(m*‖ω*)×e(g1,g2)s×e(g1,g2)z-s= ((m*‖ω*)×e(g1,g2)z-s)×e(g1,g2)s.

由于(m*‖ω*)×e(g1,g2)z-s与(Invalidm ω)属于同一分布，该结论成立.

εdbdh+PrAbort≤εdbdh+ADVCR+query/p,

引理1证毕.

游戏2.在游戏1的基础上，挑战者对挑战密文进行改动为

引理2将证明敌手视角下，游戏1与游戏2具备不可区分性.

引理2.如果G1上的XDH假设成立，则以不可忽略概率区分Game1,Game2的PPT敌手不存在.

2) 查询阶段1.

4) 查询阶段2.解密预言机添加额外限制：当C*和用户序号t作为参数被一起提交时，解密预言机输出⊥.

引理2证毕.

εIND-CCA2=Advdistinguish0,1+Advdistinguish1,2+εGame2≤εdbdh+ADVCR+query/p+εxdh+0,

其中εxdh为敌手在XDH问题中的优势.易见在定理1中述及的相关假设成立的前提下，εIND-CCA2是可忽略的.

定理1证毕.

4.2 OW-CCA2安全性

定理2.在G上的DBDH假设及H2函数的抗碰撞性成立的前提下，3.1节中提出的FG-PKEET方案对于1类敌手具备OW-CCA2安全性.

证明.为了简化证明过程，首先需模拟令牌生成的整个过程.OW-CCA2游戏中设立的令牌预言机生成token(t,i)：

类似地，一类令牌预言机生成token(t,i,Ct)的过程为

其中，m是由PKt加密所得密文Ct解密所得的明文.

二类令牌预言机以如下结构生成二类令牌token(t,i,Ct,Ci)：

其中，γ←r分别为Ct,Ci解密所得的明文.

挑战密文其他组件的生成方式与原方案描述一致.

我们将在引理3中证明游戏0和游戏1的不可区分性.

引理3.如果G上的DBDH假设成立，则以不可忽略概率区分Game0,Game1的PPT敌手不存在.

2) 查询阶段-1.

① 解密预言机.与引理1中的描述相同；

Advdistinguish0,1≤εdbdh+Prabortion≤εdbdh+AdvCR+query/p.

显而易见，在引理3中述及的相关假设成立的前提下，Advdistinguish0,1是可忽略的.

引理3证毕.

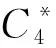
综上所述，一类敌手在OW-CCA2游戏中的优势为

AdvOW-CCA2=Advdistinguish0,1+AdvGame1≤εdbdh+AdvCR+query/p+AdvPR，

其中，AdvPR指代Hash函数H2的原像性被攻破的概率.易见敌手在OW-CCA2游戏中的优势是可忽略的.

定理2证毕.

4.3 FG-AUTH安全性

定理3.在G1,G2上的Ex-DBDH假设、G上的DBDH假设成立的前提下，3.1节构造的FG-PKEET方案在标准模型下具备针对一类敌手的FG-Auth安全性质.

证明.为证明3.1节所提及方案具备FG-Auth性质，我们需要构建一系列游戏：

游戏0.挑战者的行为与定义2的FG-Auth游戏中所描述一致.

游戏1.在该游戏中，生成关于用户Ut或Uw令牌的方法被改变，挑战者秘密地选取随机值ht,hw←rq.

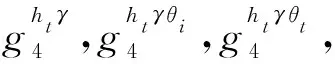
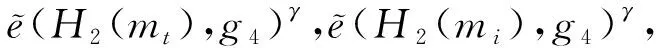
在该过程中，均需按照原方案所述，对密文进行校验.

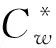
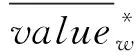
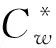
为证明游戏1和游戏2的不可区分性，我们沿用引理1的方法证明引理4.

引理4.如果G上的DBDH假设成立，以不可忽略概率区分游戏1和游戏2的PPT敌手不存在.

当b=1时，显然游戏1与游戏2对于敌手而言是不可区分的，下文中我们将证明如果当b=0时，敌手无法区分游戏1和游戏2.

2) 查询阶段-1.

② 令牌预言机：与游戏1中所述行为一致.

4) 查询阶段-2.

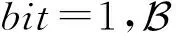
类似引理1中得出的结论，游戏1与游戏2的区分优势的上界为

Prdistinguish1,2≤query/p+ADVCR+εdbdh.

引理4证毕.

为了将FG-Auth游戏的困难性最终归约至Ex-DBDH假设，我们需要构建一系列游戏，并用与引理4相似的方法证明游戏之间的不可区分性，其原理类似于混合参数(hybrid argument).

游戏3.对比游戏2，挑战密文改动为

我们将用引理5证明游戏2与游戏3的不可区分性：

引理5.如果G上的DBDH假设成立，则不存在能够以不可忽略概率区分游戏2与游戏3的PPT敌手.

2) 查询阶段-1.

② 令牌预言机.与游戏1中所述的行为一致.

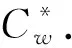
4) 查询阶段-2.

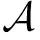
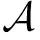
Advdistinguish2,3≤query/p+ADVCR+εdbdh.

对于PPT敌手而言其概率是可忽略的.

引理5证毕.

游戏4.挑战密文如以下方式生成，其与游戏5中挑战密文的唯一区别在于mb的赋值：

其中m#←rM.

引理6将用于证明游戏3与游戏4对于PPT敌手的不可区分性.

引理6.如果G上的DBDH假设成立，则以不可忽略概率区分游戏3与游戏4的PPT敌手不存在.

2) 查询阶段-1.

② 令牌预言机.与游戏1中所述的行为一致.

4) 查询阶段-2.

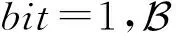
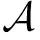
Advdistinguish3,4≤query/p+ADVCR+εdbdh.

最终，我们构建游戏5，其与游戏4统计不可区分.

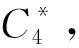
挑战密文对生成：

其中，若挑战者随机生成的比特值b=0，则赋值X=α，否则，X←rG1.

显然，游戏4与游戏5不可区分.我们将证明如果G1,G2上的Ex-DBDH假设成立，则敌手在游戏5中的优势是可忽略的.

B设置相应的密钥参数为

其余公私钥参数则根据3.1节中述及的方法正常生成.

2) 查询阶段-1.

3) 挑战阶段.与游戏5中的描述一致.

4) 查询阶段-2.

其中,γt←rq.

引理6证毕.

最终，敌手攻破方案3.1的FG-Auth性质的优势上界可表示为

AdvFG-SEC=Advdistinguish1,2+Advdistinguish2,3+Advdistinguish3,4+AdvGame5= 3×(εdbdh+AdvCR+query/p)+εex-dbdh.

显而易见，如果相应假设成立，则敌手的优势是可忽略的.

定理3证毕.

5 方案特性比对与效率比较

表1对各个PKEET方案的特性进行了描述和汇总，其中方案[1]不具备令牌机制，因而不具备针对二类敌手的IND-CCA2性质，在安全性方面逊于其余PKEET方案.由表1可见，我们所提出的方案是唯一集成了FG-PKEET与PKEET-FA方案功能性，与此同时，安全性基于标准模型的密文一致性检测公钥加密方案.

Table 1 Property Comparison of PKEET Schemes表1 PKEET方案特性对比

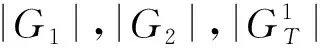
Table 2 Efficiency Comparison on Encryption/Decryption of PKEET Schemes表2 PKEET方案加解密效率对比

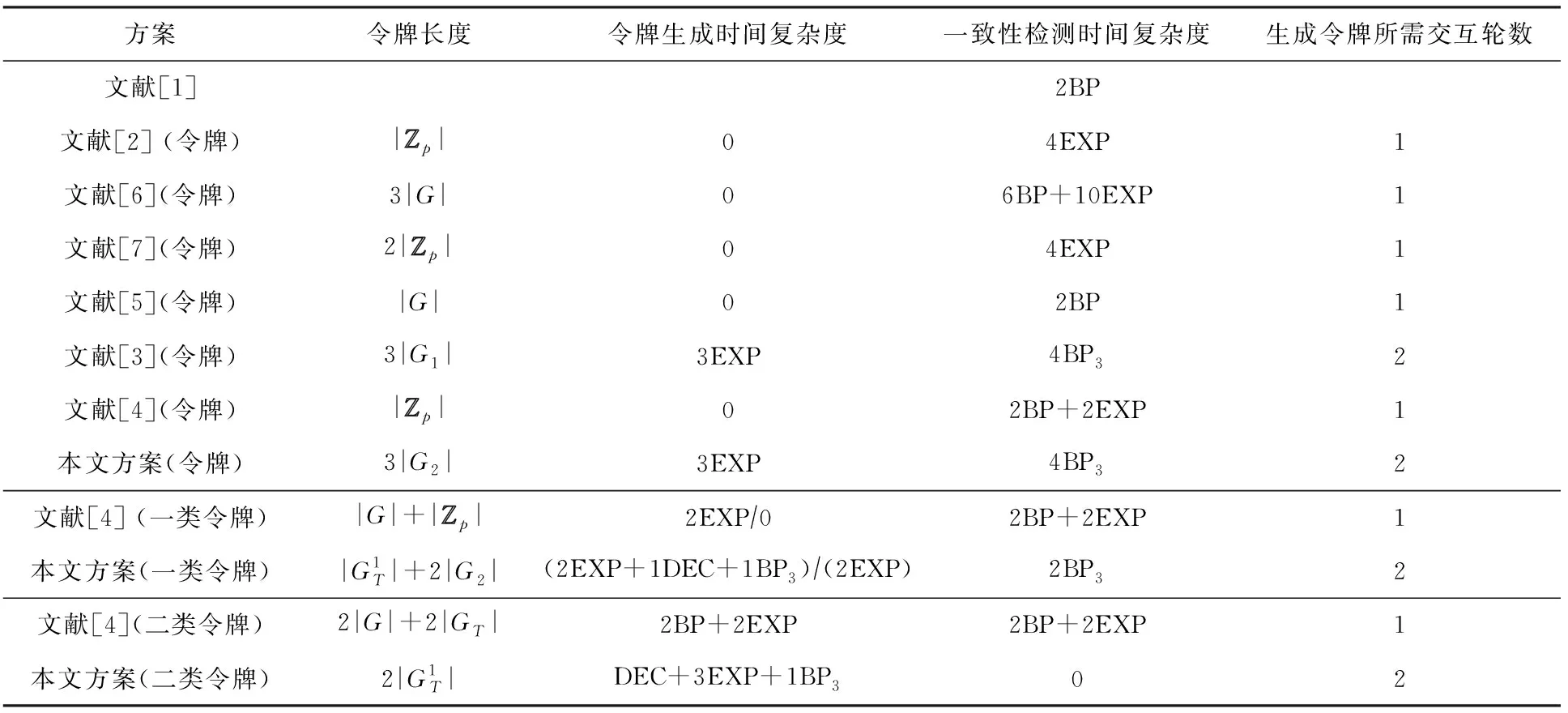
Table 3 Efficiency Comparison on Token-Related Operation of PKEET Schemes表3 PKEET方案令牌操作效率对比

由于生成一类令牌时双方用户授权客体不同，即一方授权特定一条密文信息，另一方对自己公钥加密所得的所有密文进行授权，因此在令牌生成时间上有所区别，并用符号“/”划分.

某些场合下某些方案的令牌生成时间为0，这是由于在这些情况中，令牌在公私钥对生成过程中一并生成，只需被重复地分发给代理即可完成授权.

由于Lee等人的方案[6]、Zeng等人的方案[7]均为通用型方案，因此在进行效率计算时，我们特别声明文献[6]方案采用的一次性签名方案和IBE方案分别为文献[13]方案、文献[14]方案.文献[7]方案所基于的难题为离散对数难题.

在我们的方案中，当某个用户需生成关于同一密文的多个一次、二次令牌时，只需执行一次Dec操作.由表2、表3可见，相比已有方案，我们方案在计算效率与存储开销方面相当.

6 结 论

针对当前PKEET方案在令牌授权机制方面无法兼顾弹性授权机制特性与细粒度授权机制特性的问题，本文提出了一种新的PKEET方案，该方案具备细粒度特性，即允许发放一致性检测令牌的用户能够对参与检测的另一客体进行约束.同时，该方案具备弹性授权机制，允许令牌授权的客体可在用户级别及密文级别间进行选择，结合上文提及的细粒度特性，方案的令牌类别总共可分为用户-用户令牌、密文-密文令牌及密文-用户令牌共计3类令牌，使该方案能够在令牌授权机制方面为用户提供了更细粒度的控制手段.

方案安全性方面，本文所提及方案在功能性层面的延展使我们需对方案的安全性质定义做出修改及补充，并最终证明了我们所设计方案具备适应性选择密文攻击安全性及授权细粒度安全性.相比于此前拥有细粒度特性或弹性授权机制的方案，本文所提出方案的安全性首次建立于标准模型之上在安全性方面更加具有可靠性.