挖掘数学文化 践行学科育人
王洋洋


[摘 要]基于核心素养的学科育人,必须抓住课堂主阵地,从课堂设计的细节入手,关注知识的由来,讲透问题的本质,才能实现从知识本身到学生思维方式的转化,真正达到学科育人。文章通过对一节示范课的片段呈现和点评来阐述学科育人的教学策略。
[关键词]学科育人;核心素养;数学文化;数系扩充;复数概念
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)30-0031-02
《普通高中數学课程标准(2017年版)》指出,要强调数学与生活以及其他学科的联系,提升学生运用数学知识解决实际问题的能力,同时注重数学文化的渗透,不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值。 当核心素养明确与“必备品格”和“关键能力”联系在一起时,那就意味着学科育人已经不只是德育的专利,而应该更多地以课堂学科教育这个主阵地为契机。其中,数学作为初高中教育的基础学科,数学教师也应该主动承担起提升学生智力、渗透文化、培养学生素养的责任,润物细无声地达到学科育人的目的。
复数的出现对于力学、电学和其他学科起到极大的推动作用,知识上它可以与平面向量、三角函数密切联系。更多意义上,它的应用并不像实数系一样跟我们的日常生活息息相关、触目可及。复数系更多抽象地存在于科学研究中,可以说它的出现是人类理性思维在数系扩充中的充分体现,是利用实数系中的类比进行抽象、推理而得来的数系。
如何能够上好《数系的扩充和复数的引入》这堂课,实现学科育人的目标呢?本人有幸参加了南宁三中特级教师黄河清老师召开的高中数学学科育人研究课暨成果总结会,听到了陈华曲老师关于《数系地扩充和复数的引入》的示范课,现截取几个片段,做以下思考。
[片段一]概念引入由情景导入,精准把握数学史料的“广度”和“深度”
由于复数系本身的抽象性,一些“重结论、轻来由”的教师可能会单刀直入讲复数的概念形式[z=a+bi] 及复数加减乘除计算,忽略了对虚数单位[ i]的引出,导致有的学生对于虚数系突兀地出现感到莫名其妙,一头雾水。可以说这样的做法错过了一次非常好的让学生了解数学发展史的机会,委实可惜。因为学科育人育的对象是学生,育的目的是培养学生的数学学习能力,这能力的培养中就应该包括对数学学科历史的认识。知史以明鉴,查古以至今,学生学习数学前辈攻坚克难的品质,才能勇敢地踏上征程,推动人类数学研究的巨轮继续前行。
关于“数系发展”的数学史资料非常丰富,如果教师讲得太多,一来影响教学进度,二来喧宾夺主,易脱离课堂主题。陈老师并没有采用一个个故事串联的方式进行讲解,而是收放自如地在浩瀚的数学史料中取其所用。陈老师结合PPT展示数的发展史,利用图片展示来讲解数系的扩充历程。板书内容:自然数集N→整数集Z→有理数集Q→实数集R。考虑到有的学生理解虚数有困难,陈老师力图创造构建新概念的心智条件,使学生先形成对新数系的感性认识。学生通过PPT的展示可以得到结论,当数的发展不能满足人类的使用需求时,就到了要扩充数系的时候。正如恩格斯所说:“数学像所有别的科学一样,起因于人们的需要。”数系发展的历程体现了人类探索世界、认识世界的历程。陈老师水到渠成地讲明白了数系扩充的必要性。
当我们在实数系内无法找到[x2+1=0 ]根时,该如何解决这个数学问题呢?陈老师适时抛出这个问题,引导学生像数学家一样去思考,此时竟然出现了实数系内不能解决的问题,学生自然有兴趣去探究新知。
引入新事物——虚数单位[i],规定[i2+1=0]。
对于虚数单位[i],值得一提的是,为何要用[i]这个字母,而不用其他的字母?陈老师在课堂上讲述了这个史料。莱布尼茨曾经说过:“虚数是神灵遁迹的精微而奇异的隐蔽所,它大概是存在和虚妄两界中的两栖物。”正由于它没有实体存在,所以有个有趣的简称,用“imagine”(想象)的首字母[i]表示,所以虚数可以说是“幻想之数”。学生听后恍然大悟,会心一笑。学生亲身体会到数的“发现”与“发明”过程,整个授课过程不拖沓烦冗,陈老师精准地把握了史料的“广度”和“深度”。
[片段二]数系扩充中“规则”意识的强调必不可少
如果没有运算,那么数只是孤立的符号。在讲授复数概念后,陈老师开始引导学生去探求数系扩充中的“规则”。她提问:“数系扩充后,在运算上遵循什么规则?”所谓的规则,其实就是大学《近世代数》中提到的数系对加减运算各种算子的封闭。找出“规则”是本节课的难点。学生对于规则的归纳用了较长的时间,本人听课时觉得陈老师在此处的提问有些抽象,可能可以更具体地引导学生。
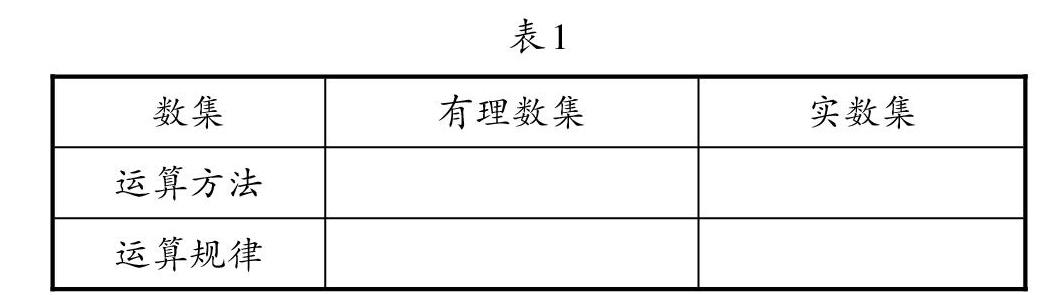
比如,以有理数集在引入无理数之后扩充到实数集为例。可以引导学生小组学习填写表1。
有了表1的指向性,在该教学环节中学生得出如下表2的答案就不太困难。
陈老师引导学生得到结论:数系扩充后,在新数集中规定的加减乘除运算与原数集中规定的加减乘除运算协调一致,并且加法和乘法都满足交换律和结合律,乘法对加法满足分配律。
在“规则”的指导下,学生也考虑到使得方程[x2+1=0]有解,从而可以像实数一样进行加减乘除,成功地将实数系添入虚数之后扩充为复数系。在寻找这个“规则”时,循循善诱的提问和启迪过程让学生体会类比的数学思想,培养了学生的逻辑推理和抽象概况能力。
在教学过程中让课堂变成学生勇于“尝试”的课堂,通过学习“活动”让学生感受知识的奥秘,这就是黄河清老师“三环耦合”的育人模式通过“思维育人、史料育人、审美育人、活动育人”四个维度加强学科育人的集中体现。
如何让核心素养落地生根,让学科育人落实到课堂?本人认为,只有这种精雕细琢的课堂设计,教师把握好授课的各个环节、各个维度才能真正实现学科育人,否则核心素养的培养很容易落为空谈。
[片段三]条理清晰地对数系归类
有了虛数单位后,陈老师引导学生自己根据“规则”自由地举例子。学生利用“规则”指引,大胆发言,给出了如下多个复数的例子。
实数:5、2、1、0
新数:[i ]
利用“规则”自由组合得到的复数:[5+2i]、 [2+5i]、[5i]、[i]、0
观察多个复数例子,陈老师提问:能否将这些复数写为一个统一的形式?这是对学生数学抽象概括能力的考查。核心素养是教育界的热门话题,但是如何判断学生是否具备高中数学的六大核心素养呢?比如六大核心素养中的“抽象概括”素养,它具隐性且不易衡量,如果学生能够用语言表达概括出复数的代数形式可以统一写为[z=a+bi],并能够给出合理解释时,我们就有充分理由相信学生具备这一素养。
“如何根据形式特点对数系归类?”陈老师又抓住契机提出了新问题。
学生陷入思考,不一会儿,陈老师展示了学生画的venn图,并解释自己的分类标准,如图1所示。
该生的表现非常精彩,赢得在场老师的啧啧称赞。数学语言、文字语言、图形语言的转化该生运用得游刃有余,非常熟练。
然后师生合作,填写分类结果。
复数[z=a+bi实数b=0虚数b≠0纯虚数(a=0,b≠0)非纯虚数a≠0,b≠0]
最后,陈老师让学生试着从知识、方法、数学思想、经验等方面谈谈本节课有哪些收获。除了知识层面外,学生还谈到数学家也曾有不易解答的难题。小小的[ i] 经过了两个世纪的努力才被世人所接受。我们只有跳出原有的旧框架,勇敢地“更新观念”,才会发现更为广阔的数学天地。
整个课堂中,陈老师都让学生感受到数学家就在自己的身边。从发现i,到在“规则”的指导下顺利扩充数系,并对数系进行归类整理,体验与数学家一起“发现问题→思考问题→解决问题”的过程。
总之,教师只有专注教材的每个细节,立足课堂,精准把握学生的起点、困难和需求,给予正确的指导和帮助,敢于放手、善于引导,让学生自由表达,并对学生耐心启发,浸润、激励和引导学生,才能真正地以本学科的特质为载体来达到学科育人的目的,实现学生的自我成长。
(责任编辑 黄诺依)

