基于关节刚度辨识的机器人加工过程姿态优化

段现银，张 樵，朱泽润，张 灿，李澜涛，蒋国璋

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.深圳市汇川技术股份有限公司研发管理部技术中心，广东 深圳，518109)

随着工业自动化的发展，工业机器人加工精度和稳定性能不断提升，其有望代替价格昂贵的机床，广泛应用于加工制造、自动化控制等领域[1-2]。凭借灵活性好、智能化程度高、工作空间大、设备成本相对较低等诸多优势，工业机器人的应用范围从早期的搬运、装配和扫描等非加工操作扩展到焊接、抛光和铣削等加工操作，成为制造强国战略中的核心装备[3-4]。相对于稳定性较高的机床，工业机器人多关节串联结构使其具有典型的弱刚度特性[5]，其末端在负载作用下产生较大力致变形使得待加工面在法矢方向产生较大误差，其最终影响加工精度，因此，有必要对机器人刚度进行研究，优化机器人刚度性能，提高其稳定加工能力。研究人员对机器人刚度的研究主要集中于刚度性能分析、刚度建模和关节刚度辨识[6]。

工业机器人笛卡尔刚度随着其构型的变化而改变，故可建立相关指标评估机器人刚度，优化机器人构型以增强刚度性能。Guo等[7]提出基于柔度椭球体积的刚度性能评价指标，研究了冗余轴相关的刚度值变化规律，用于优化机器人姿态。Xiong等[8]针对机器人冗余问题，设计了进给方向刚度性能评价指标，优化加工系统沿进给方向的刚度性能，得到最优构型。Ling等[9]根据机器人运动学性能和形变评估指标，绘制加工性能图进行钻孔姿态优化。Liao等[10]划分加工曲面区域，以曲面法向和切向柔度系数为性能指标，分区域优化机器人冗余度和刀具进给方向，提高机器人铣削加工精度。

工业机器人的刚度建模以及刚度参数识别在其加工制造过程中起着重要作用[11]。Dumas等[12]分析机器人灵巧性对刚度建模的影响，通过实验辨识的关节柔度系数获得关节刚度矩阵。曲巍崴等[13]基于传统刚度映射模型，通过激光跟踪仪测量不同压脚压力和机器人姿态下末端变形，获得钻孔机器人关节刚度。芮平等[14]建立关节刚度误差模型，并在机器人几何参数标定的基础上利用改进遗传算法实现关节刚度参数辨识。郭英杰等[15]建立了考虑压脚与工件间摩擦力的钻孔机器人刚度模型，并基于L-M算法辨识出关节刚度。

上述研究在机器人关节刚度参数辨识和刚度建模上取得了较多进展，但均限于机器人静态工况下进行刚度参数识别，且辨识实验中所使用的激光跟踪仪价格昂贵，而在实际的工业机器人应用中，机器人末端力致变形通常会随机器人姿态变化而改变，因此，有必要在加工过程中对关节刚度进行辨识，以符合机器人实际应用工况，工业机器人的广泛应用也使得采用激光跟踪仪进行刚度辨识存在明显的实际条件限制，有必要考虑兼具测量精度和推广意义的辨识方法，并将其应用于机器人加工过程优化。为此，本文针对工业机器人末端因其弱刚性在负载作用下产生较大力致变形问题，首先构建ABB IRB1410六自由度工业机器人正运动学模型、末端柔度与力致变形模型，再应用工业机器人加工运动过程中基于多位移传感器的关节刚度辨识方法，以法向刚度性能指标作为优化目标建立机器人姿态优化模型，设计模型求解方法优化机器人姿态，并通过重力负载实验获取机器人关节刚度值以及验证该方法在优化机器人姿态、提高其末端刚度性能方面的有效性，以期为降低工业机器人末端力致变形、提高其加工精度提供参考。

1 机器人运动学建模

机器人运动学建模是后续建立机器人柔度模型以及优化机器人刚度性能的基础。本文研究对象是六自由度工业机器人，型号为ABB IRB1410-5/1.45，根据此机器人的结构参数，运用D-H方法建立机器人的运动学模型，如图1所示。在图1(b)中，OB为机器人基坐标系原点；Oi为对应于关节i(i=1, 2, …, 6)的坐标系原点；ai为臂杆长度；di为臂杆偏置距离。

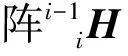
(1)

式中，αi-1为机器人臂杆角度；qi为i关节的关节角。

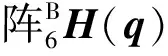
(2)

式中，每个元素均为关节角q= [q1,q2,q3,q4,q5,q6]T的函数且由机器人D-H参数(见表1)确定。

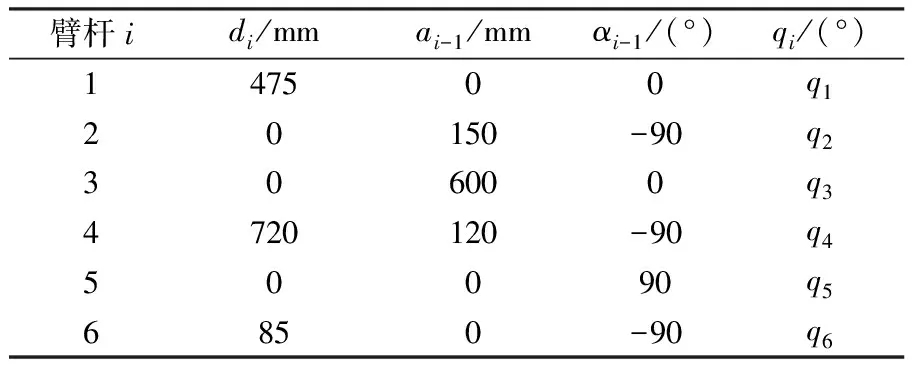
表1 ABB IRB1410机器人D-H参数

2 机器人关节刚度辨识

2.1 机器人柔度及力致变形建模

机器人刚度反映其在外力作用下抵抗变形的能力，当机器人臂杆和末端执行器具有较好刚度特性时，其刚度模型为K=J-TKqJ-1。因柔度矩阵C为刚度矩阵K的逆矩阵，采用柔度矩阵C代替刚度矩阵K可避免求解雅可比矩阵J的逆矩阵，本文基于此进行机器人柔度建模。

机器人的柔度矩阵C、雅可比矩阵J和关节刚度矩阵Kq为6×6矩阵，按照矩阵元素的物理意义，可将其分为四个3×3的子矩阵，具体为：

(3)

式中，Ctt为平移柔度子矩阵；Crr为旋转柔度子矩阵；Ctr为耦合柔度子矩阵；雅可比矩阵J由D-H参数计算得到；对角矩阵Kq为机器人的关节刚度；雅可比矩阵J和对角矩阵Kq的矩阵描述分别为：

(4)

基于柔度矩阵C，可得机器人末端变形ΔX与其作用力F之间的关系为：

(5)

式中，ΔX为机器人末端上的平移(mm)和旋转位移(rad)；F为作用在机器人末端上的广义力，包括力(N)和力矩(N·m)。矩阵描述为：

(6)

假设作用在机器人末端执行器上力矩很小，对平移变形的贡献微小，可忽略作用力矩及其引起的旋转变形，将公式(5)转换为：

(7)

式中，ΔXt=[dxdydz]T为ΔX中的平移位移部分，即为机器人末端力致变形；Ff=[F1F2F3]T为F中作用力部分。

将公式(3)代入公式(7)，得到力致变形ΔXt为：

(8)

2.2 关节刚度辨识方法

由机器人力致变形模型可知，机器人末端力致变形ΔXt与关节刚度子矩阵K11和K22、雅克比子矩阵J11和J21以及作用力Ff相关联。在机器人加工过程中，雅克比子矩阵K11和K22随机器人构型变化发生改变，在获取机器人姿态q下可根据D-H参数计算得到；机器人力致变形ΔXt和末端作用力Ff的数据可通过激光位移传感器和测力仪获取。基于此，建立机器人加工过程关节刚度辨识系统，如图2所示，通过该系统获取机器人关节刚度矩阵Kq。在图2中，关节刚度辨识系统主要由工业机器人、激光位移传感器测头、传感器控制器、传感器对应的参考平面、测力仪、固定夹具、滑轨滑块装置和PC等组成。激光位移传感器射出激光打在对应参考平面上，其测量距离因机器人末端力致变形发生变化，故可通过传感器1、传感器2和传感器3分别测量加工过程中机器人末端力致变形在XB、YB和ZB轴方向的分量。假定XB轴方向为末端执行器进给方向，为获取该方向上传感器的测量数据，则参考平面1需与机器人同步运动(参考平面2和3为静态参考面)，将其安装在滑轨滑块装置上，根据机器人示教器上进给速度，保持电机驱动滑块速度与之相同，使传感器1和参考平面1的距离保持在测量范围内。

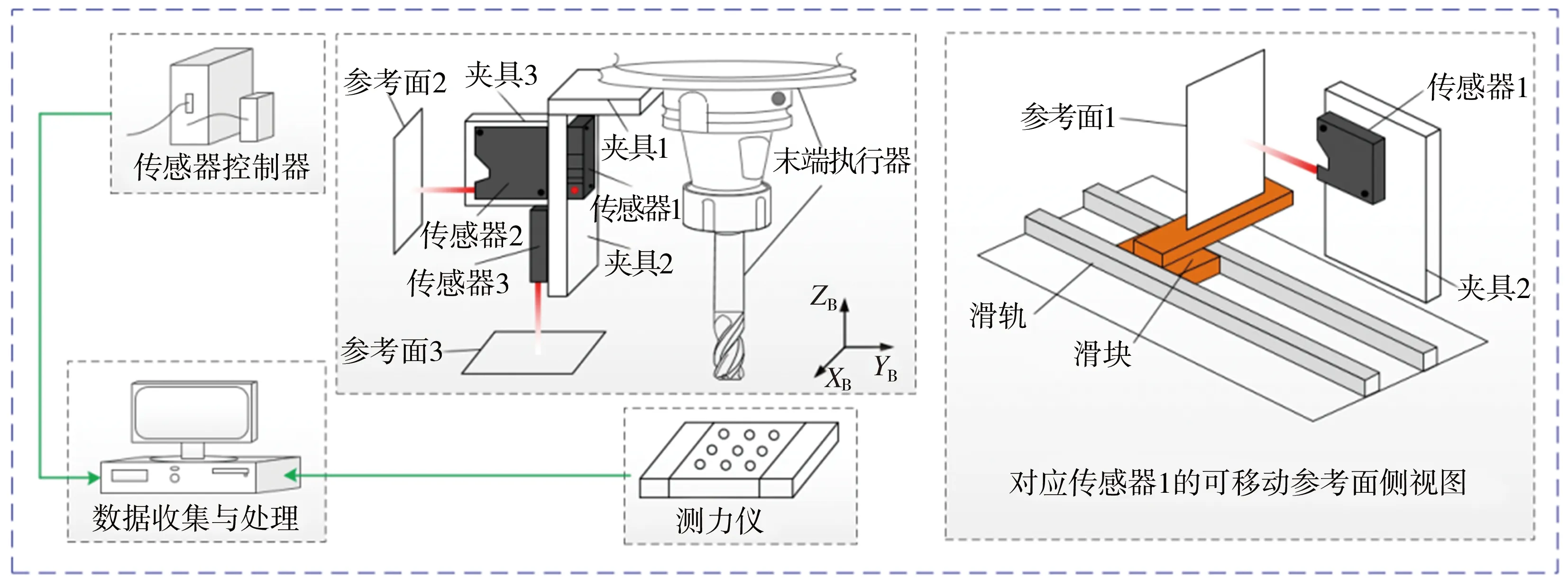
图2 机器人加工过程关节刚度辨识系统

在关节刚度辨识系统中获取机器人力致变形ΔXt和末端作用力Ff后，将公式(8)中关节刚度分离出来，则可展开得到：

=Ac

(9)

式中，矩阵c为各关节柔度值组成的单列矩阵；矩阵A为机器人雅可比矩阵J和作用力Ff确定的矩阵，分别描述如下：

(10)

(11)

从公式(9)中可以看出求解关节刚度辨识矩阵方程组Ac=ΔXt可获取关节刚度Kq。因方程组的系数矩阵A为3×6的矩阵，则最少需获取2组A和ΔXt数据使方程组为超定方程，并根据最小二乘法得到矩阵方程组的解向量c应满足最小化误差：

f(c)=min‖Ac-ΔXt‖2

(12)

当f(c0) = 0时，c0=AIΔXt为方程组的解，即Ac0=ΔXt，AI为A的广义逆矩阵。

2.3 关节刚度辨识实验

图3为机器人关节刚度辨识实验现场，考虑机器人末端负载范围(0～5 kg)以及传感器安装位置，设计专用传感器夹具安装于法兰盘上，且材料均为铝合金。本文以重物作为负载模拟机器人加工过程末端受力，避免了对测力仪数据的处理，利于简化辨识实验。实验中使用超高速激光位移检测仪测量机器人末端力致变形，其传感器测头型号分别为Keyence LK-H020(传感器测头1和传感器测头2)和Keyence LJ-V7080(传感器测头3)。

图3 关节刚度辨识实验现场

实验前，操作机器人移动到合适位置使关节6的Z6轴保持水平，并编程滑轨电机速度与示教器中写入的机器人进给速度相同。考虑工业机器人可达性和参考平面的设置范围，本实验共选取5组不同的机器人初始姿态，各姿态下机器人关节角度如表2所示。在每组初始姿态下，机器人沿XB轴方向线性运动，其进给速度和运动行程分别为20 mm/s和400 mm，并且在运动行程中选取4个位置的机器人末端力致变形作为实验数据。为避免系统误差及安装误差等影响，如传感器测头发射激光倾斜所引入的误差及参考面的平面度误差，分别采集其末端施加负载前后机器人在相同路径上力致变形，两次采集数据差值作为公式(12)中的ΔXt值。

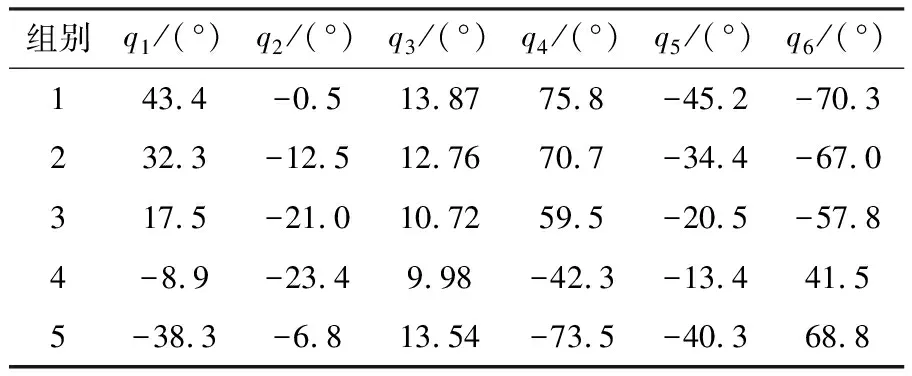
表2 5组不同初始姿态机器人的关节角度

由上述关节刚度实验共获取20组实验数据，故关节刚度辨识矩阵方程的系数矩阵A为60×6的矩阵，基于前文中关节刚度辨识方法，计算得到ABB IRB1410工业机器人各关节刚度Kq1、Kq2、Kq3、Kq4、Kq5和Kq6分别为5.34×108、3.60×108、1.58×108、5.96×107、2.27×107和3.43×106N·mm/rad。

3 机器人刚度性能优化

3.1 基于刚度性能指标的优化建模

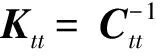
机器人末端力致变形在加工时会映射到工件表面产生力致误差，且工件表面法向上的变形最终影响其加工精度，因此，文献[6]中提出了机器人末端法向刚度指标Kn为：

(13)

式中，np为工件表面法向矢量，且np=(nx,ny,nz)T。

通过该法向刚度指标可评估和分析机器人末端刚度，基于此进行加工过程规划可减小机器人末端力致变形。

机器人末端坐标系及冗余角示意图如图4所示。六自由度工业机器人在加工中仅通过五个自由度即可确定末端执行器位姿，其导致机器人存在一个冗余自由度，使得图4中重物负载在相同位姿下可绕ZC轴旋转不同角度。不同冗余角θ导致不同机器人姿态，故可分析机器人姿态与冗余角关系，通过优化机器人冗余角来改善机器人构型。根据机器人末端点P处位姿和冗余角θ，确定机器人执行器末端到机器人基坐标的位姿变换矩阵为：

(14)

式中，(u,v,w)为点P处坐标系OC-XCYCZC相对基坐标系OB-XBYBZB的姿态矩阵，且u=(ux,uy,uz)T，v=(vx,vy,vz)T，w=(wx,wy,wz)T；(Px,Py,Pz)T为OC原点相对基坐标OB-XBYBZB的位置矢量。

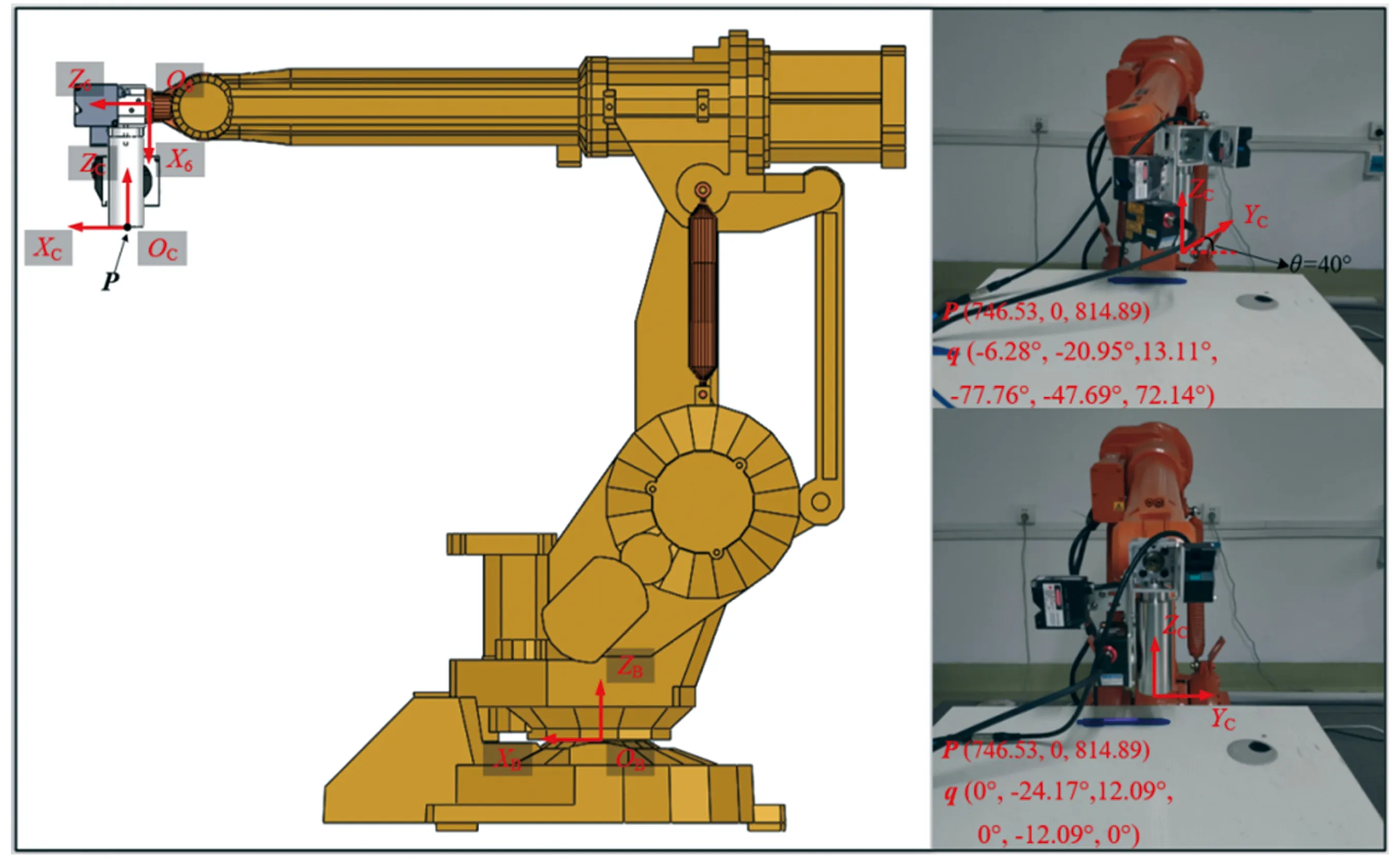
(a)机器人末端坐标系 (b)不同冗余角对应相同P点处位姿

机器人执行器末端到法兰盘的位姿变换矩阵由设计的夹具位姿决定，根据夹具设计数据和实际安装情况，具体为：

(15)

由式(2)、(14)和式(15)得到机器人姿态与末端点P的坐标值以及冗余角θ的关系如下：

(16)

式中，f[·]-1定义为逆解运算，应用pieper准则计算机器人关节角q。

综上所述，以法向刚度指标Kn作为优化目标，以冗余角θ作为优化变量，以机器人关节运动范围作为约束条件，建立机器人姿态优化模型，通过最大化法向刚度指标Kn，获取更好机器人姿态，以提高机器人刚度性能，减小其末端力致变形。机器人姿态优化模型为：

(17)

式中，Aq为关节角q的范围集合。

3.2 优化模型求解及实验验证

(18)

优化模型的求解流程如图5所示。在优化模型中，不同冗余角θ所对应的机器人关节角q以及该姿态下法向刚度指标Kn均不相同，可通过遍历θ的所有值(-180°≤θ≤180°，间隔1°)，运用公式(13)、(16)和(18)来计算重物负载绕ZC轴完整旋转内所有法向刚度指标值Kn。搜索法向刚度指标的最大值Knmax，以输出最优机器人冗余角θopt。

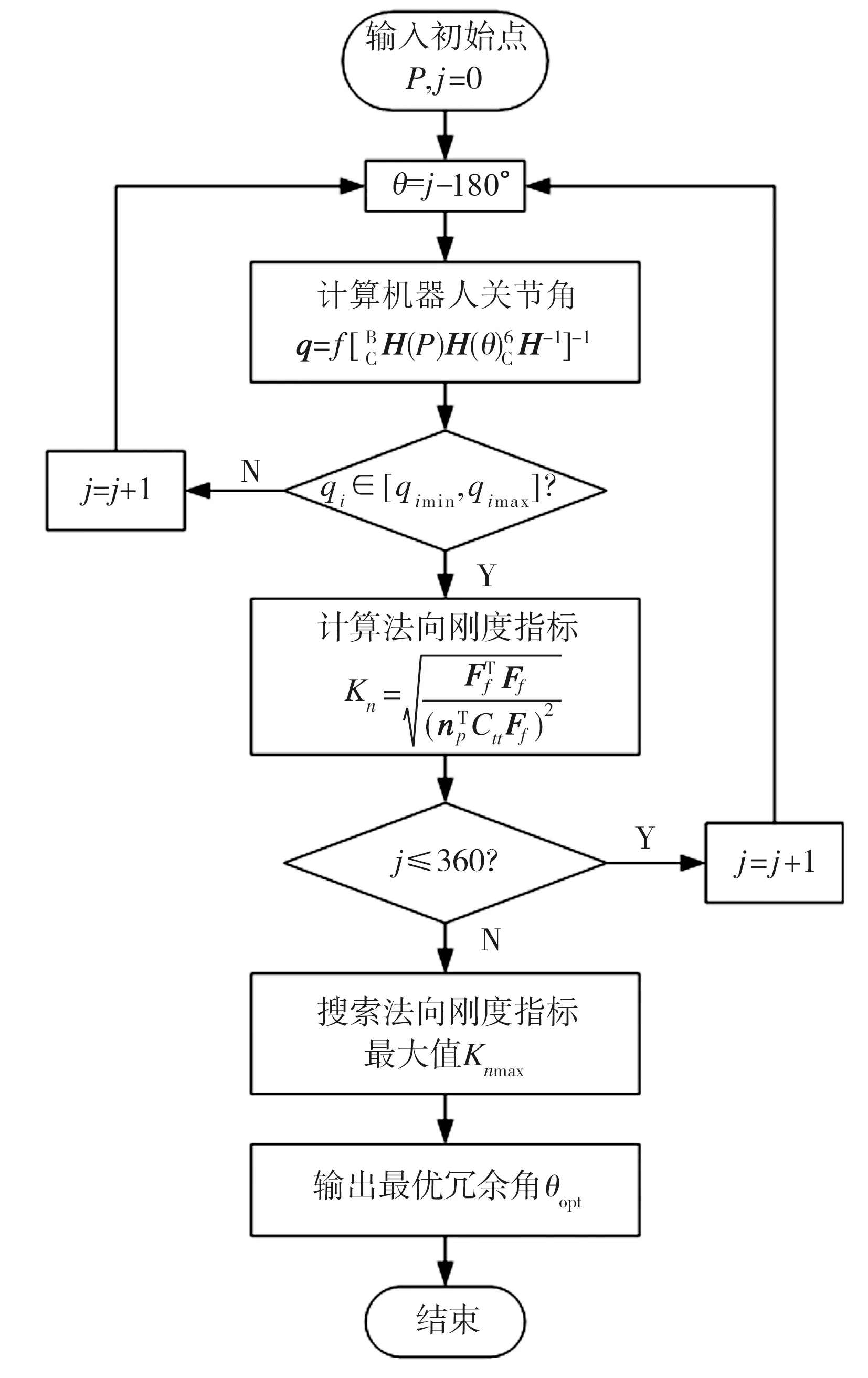
图5 优化模型求解流程

为了对所提出的优化模型进行验证，在ABB IRB1410工业机器人加工平台上设置了检测实验，图6为优化模型验证实验现场。实验中，机器人沿XB轴方向线性运动，所用传感器测头(Keyence LJ-V7080)固定于传感器3所在位置(见图6(a))，其激光点射在工作台面上，分别采集机器人末端施加负载前后其在相同路径上力致变形，两次采集数据的差值在工件表面法向的投影即为法向力致变形。

为实验简便，文中假设工件加工面为平面，则在机器人基坐标系下工件表面法向矢量np为(0, 0, 1)T，并以重力负载作为沿加工面法向上的力，主要考虑沿加工面法向上的力对机器人末端法向刚度指标的影响。在实际加工中，一般选择冗余角为0°的机器人姿态( 见图6(b))进行加工，通过优化模型求解方法选取冗余角为75°的机器人姿态(见图 6(c))进行试验，并与冗余角为0°时的试验进行对比，以此分析冗余角优化效果。冗余角优化前后机器人初始姿态和法向刚度指标如表3所示。从表3中可以看出，冗余角为75°较冗余角为0°的机器人姿态下计算得到的法向刚度指标要大。

(a)传感器测头安装位置 (b)冗余角θ为0°时实验 (c)冗余角θ为75°时实验

表3 冗余角优化前后机器人初始姿态和法向刚度指标

图 7和图 8分别为冗余角优化前后机器人末端法向刚度指标和法向力致变形。从图 7和图 8中可以看出，优化后的机器人法向刚度指标整体高于优化前的法向刚度指标，优化后的机器人末端法向力致变形整体小于优化前的机器人末端法向力致变形，这是由于在相同的加工环境下，机器人刚度是其变形改变的主要影响因素，机器人法向刚度指标越大，表明其末端在该方向的刚度性能越好，故法向力致变形越小，由此表明，机器人的末端法向力致变形与法向刚度指标紧密相关，机器人的法向刚度指标越大，其末端法向力致变形则越小。从图 7和图 8中还可以看出，随着机器人末端沿XB轴正向运动，优化前的法向刚度指标先增大后减小，而法向力致变形先减小后增大；优化后的法向刚度指标逐渐减小，而法向力致变形逐渐增加，这是因为，优化后的机器人在运动过程中其臂杆向前伸展，降低了机器人末端刚度，故其末端法向刚度指标逐渐减小，导致法向力致变形逐渐增大。从图7中还可以看出，在零采样点处，优化前后机器人法向刚度指标变化最大，优化前和优化后的机器人法向刚度指标分别为213.6、275.7 N/mm，其优化后的法向刚度较优化前提高了29.1%。从图8中可以得到，优化前和优化后机器人末端法向力致变形平均值分别为0.149、0.087 mm，其优化后的法向力致变形平均值减小了0.062 mm，减小率高达41.6%。由此可见，通过改变机器人冗余角优化机器人姿态，能够提高机器人刚度，从而可显著降低机器人末端法向力致变形，验证了该优化模型的有效性。

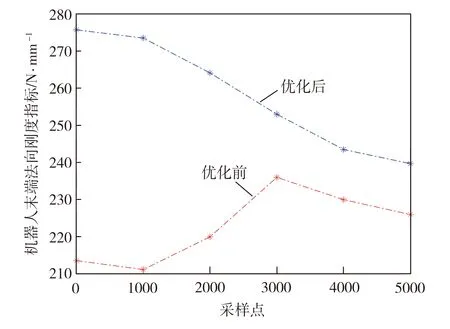
图7 冗余角优化前后机器人末端法向刚度指标

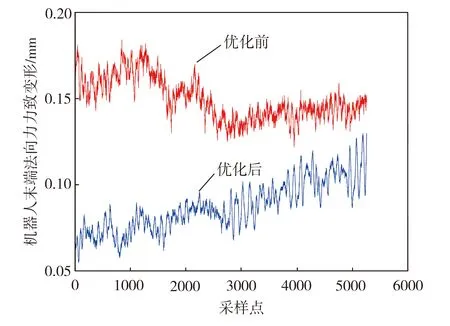
图8 冗余角优化前后机器人末端法向力致变形

4 结论

(1)以机器人冗余角为优化变量、法向刚度性能指标作为优化目标建立机器人姿态优化模型，设计模型求解方法优化机器人姿态，该优化方法能够有效提高机器人刚度性能指标和控制机器人末端的力致变形，有利于提高工业机器人的加工精度。

(2)与机器人加工运动过程姿态优化前比较，优化后机器人末端的法向力致变形减小41.6%，法向刚度最大增加29.1%。