基于半刚性结点梁单元的石墨烯振动特性分析

黄立新，叶太智，吴 宇，余 朋

(1. 广西大学土木建筑工程学院, 广西 南宁，530004；2. 广西大学工程防灾与结构安全教育部重点实验室, 广西 南宁，530004)

Novoselov等[1]利用机械剥离法于2004年首次将石墨烯从石墨中成功分离，石墨烯因具有优异的力学、光学、电学性质而受到广泛关注。石墨烯强度超高，Lee等[2]通过实验测得其杨氏模量约为1.0 TPa，理论强度约为130 GPa，此外，它还具有极高的振动频率，常被用于制造纳米级谐振器和传感器[3-4]。

因石墨烯尺寸为纳米级，实验操作难度极大，故而常借助原子模拟方法来研究其力学行为[5-7]。原子模拟方法如密度泛函(DFT)法和分子动力学(MD)法都具有很高的精度，但相应的计算量也很大，并且使用MD法不能直接求解石墨烯振动特性之类的特征值问题。相比原子模拟方法，分子结构力学方法计算效率更高，经常用于研究具有较大尺寸的石墨烯。该方法主要基于原子势能和梁应变能等效的原理，将石墨烯中的碳碳键等效为梁单元，建立刚性结点杆件模型来分析其力学性能并已获得了较好效果[8-11]，然而刚性结点杆件模型不能模拟键角变化，导致模拟结果精度不足，而半刚性结点杆件模型中的梁单元在结点处可发生相对转动来模拟键角变化，与真实石墨烯晶格受力变形基本一致，因此，考虑到石墨烯分子结构中键角变化的特点，本文提出利用半刚性结点杆件有限元模型来研究石墨烯振动特性，并借助ABAQUS平台用户自定义子程序(UEL)研究了手性、边界条件、尺寸等因素对石墨烯固有频率的影响。

1 半刚性结点杆件的有限元模型

1.1 石墨烯的杆件模型

单层石墨烯呈二维蜂窝状结构(见图1)，每个碳原子和周边3个碳原子通过σ键连接，σ键平衡键长r为0.1421 nm[12-13]，σ键夹角θ为120°。3个σ键确定1个σ平面，在σ平面法线方向上形成π键，由σ键和π键决定的平面称为π平面。

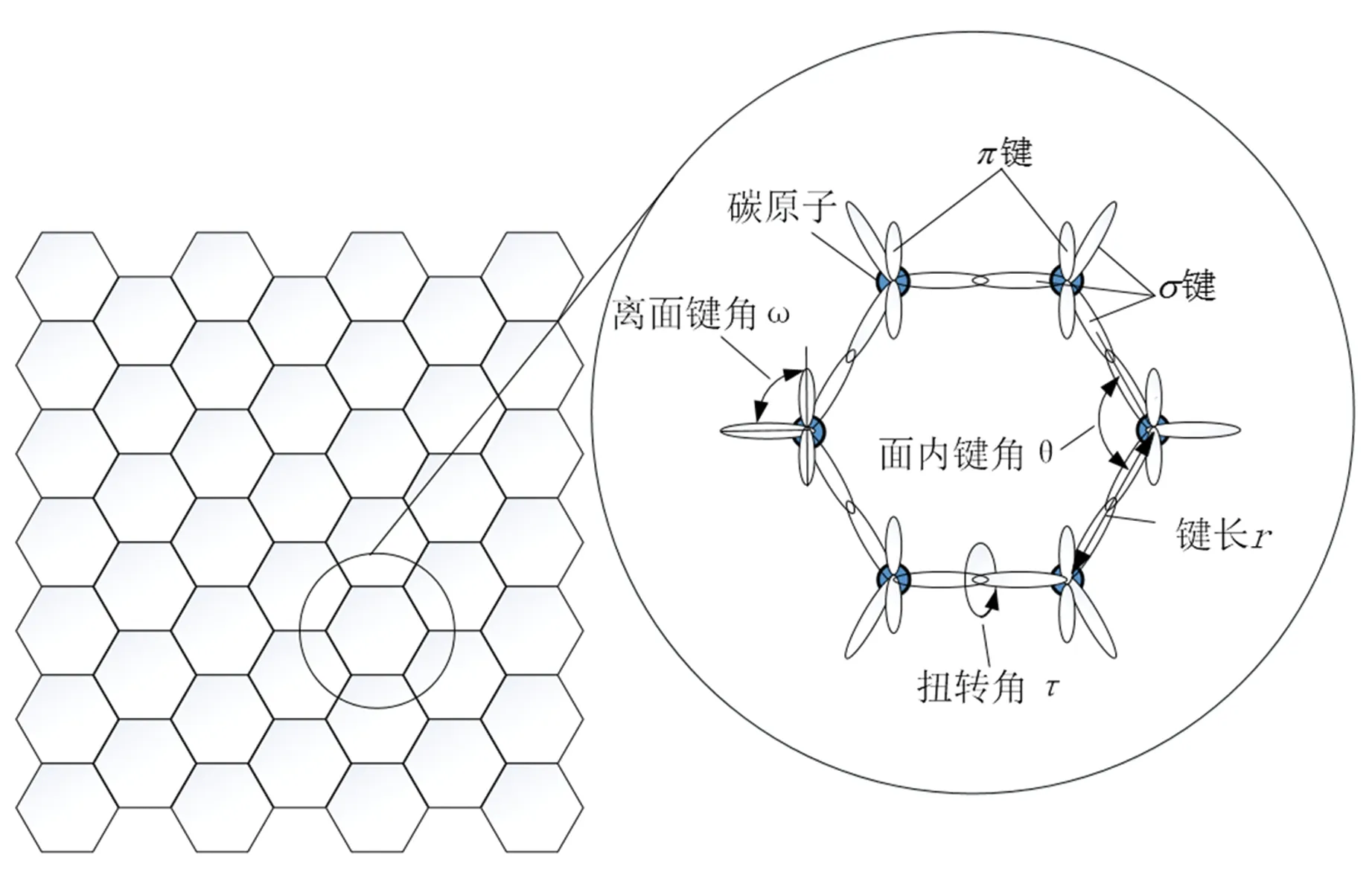
图1 石墨烯分子结构

将碳原子作为杆件之间的连接点，建立石墨烯分子结构杆件系统模型如图2所示。可利用该模型模拟石墨烯分子结构中碳碳共价键的拉伸、压缩、面内键角以及离面键角的变化，从而反映出石墨烯的受力变形情况。

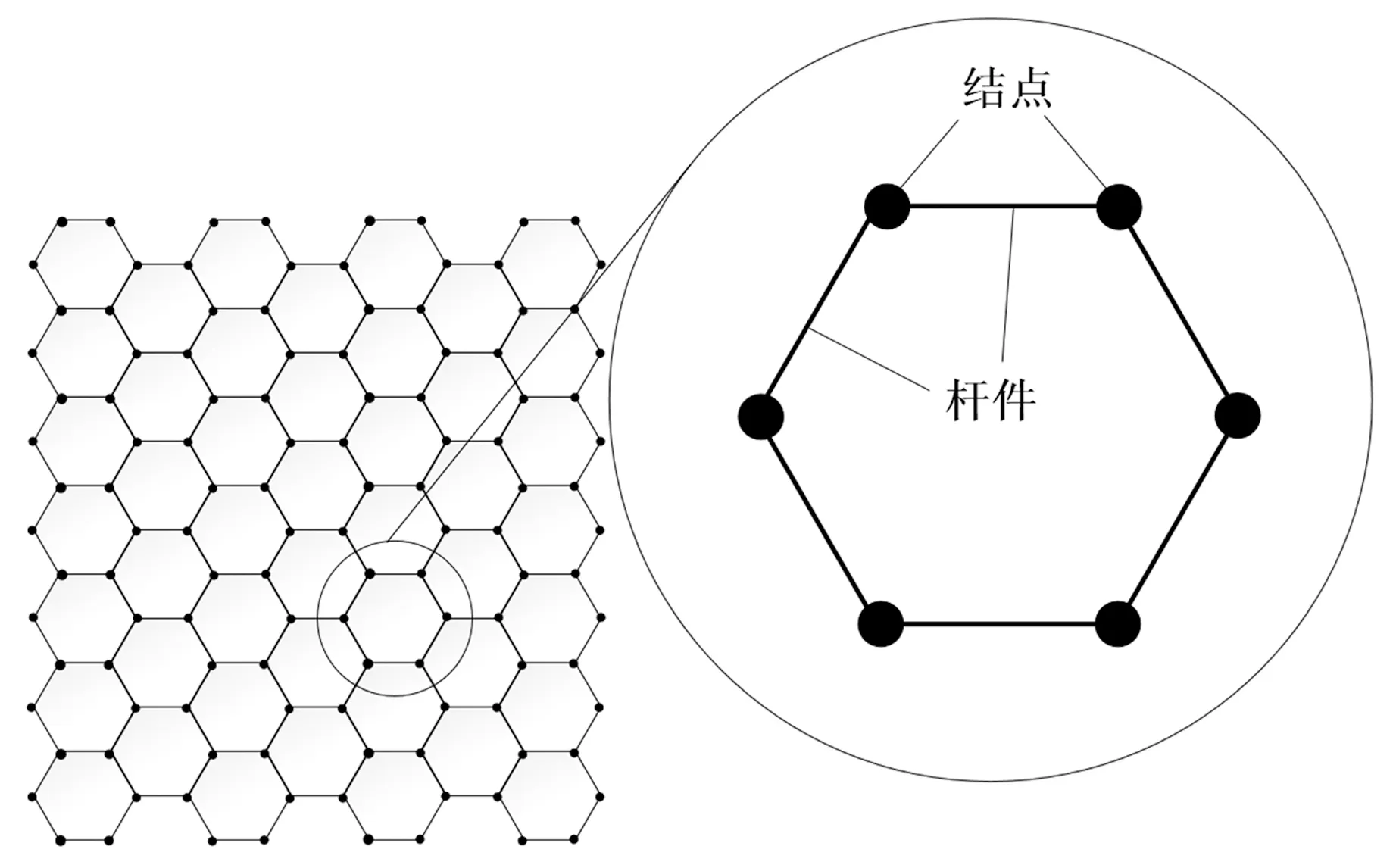
图2 石墨烯杆件结构

1.2 分子力学的势能表达式

在忽略范德华力及静电力作用的情况下，石墨烯碳碳键的总势能Utotal为：

Utotal=Ur+Uθ+Uω+Uτ

(1)

式中，Ur为碳碳键的拉伸势能，Uθ为面内键角变化势能，Uω为离面键角变化势能，Uτ为二面角扭转势能，其中Ur和Uθ的表达式分别为：

(2)

(3)

考虑到在小变形情况下谐和势函数足以描述原子势能，为简单起见，将Uω与Uτ合并，有：

(4)

式(2)～式(4)中，dri表示第i号键的伸长量，dθi表示第i号键的面内键角增量，dφi表示第i号键的二面角扭转增量；kr、kθ、kτ均是分子力学常数[14]，相应值分别为6.52×10-7N·nm-1及8.76×10-10、2.78×10-10N·nm·rad-2。

1.3 半刚性结点梁单元参数与石墨烯分子力学常数的关系

通过观察式(2)～式(4)可知，相应的谐和势函数分别是关于键增量dr、dθ和dφ的二次函数，这在函数形式上与梁分别在纯拉伸、纯弯曲及纯扭转情况下的应变能表达式相同，因此可以根据能量等效原理将碳碳键等效为梁结构来模拟碳碳键的力学行为。采用半刚性结点梁单元等效碳碳键建立半刚性结点杆件模型，结点圆截面梁单元如图3所示。该梁单元长度为L，由2个广义弹簧和中间杆件梁单元串联而成，广义弹簧是一种抽象弹簧，具有拉伸刚度k1、弯曲刚度k2及扭转刚度k3。因本文仅考虑碳碳键的键角变化，故设广义弹簧k1和k3均为无穷大且其长度忽略不计。

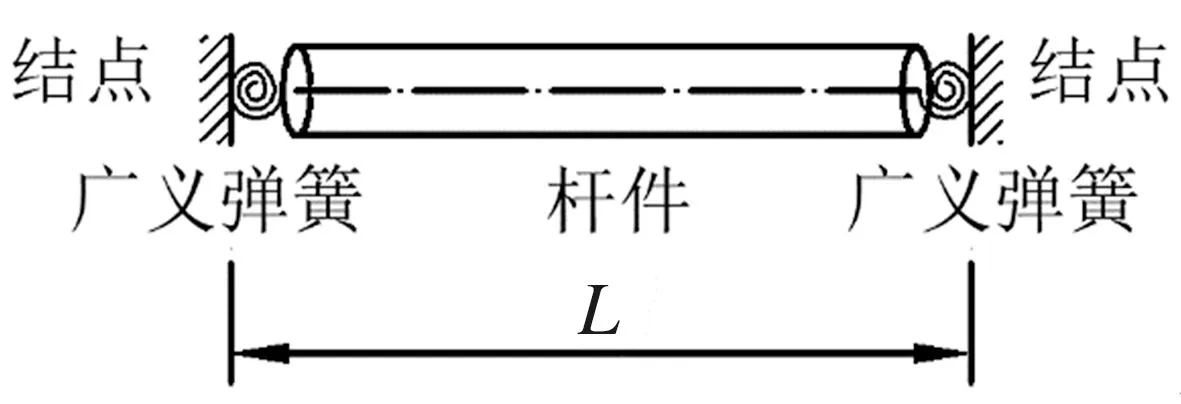
图3 等效半刚性结点梁单元

假设半刚性结点梁单元与碳碳键变形量相同，即其单轴拉伸伸长量、纯弯曲转角、纯扭转转角分别为dr、dθ及dφ，该梁单元的纯拉伸、纯弯曲及纯扭转工况如图4所示，其中F、M和T分别为梁单元所受的拉伸作用力、弯矩及扭矩，dθ为梁单元结点的相对转角，dθ1和dθ2分别为中间杆件的相对转角及单个弹簧的转角。

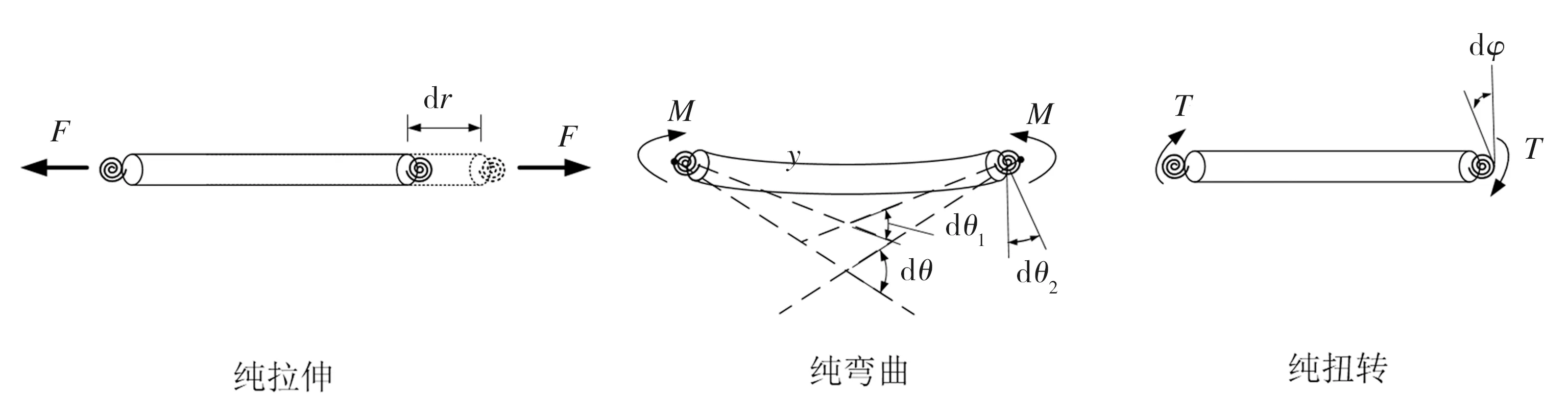
图4 半刚性结点梁单元的单轴拉伸、纯弯曲、纯扭转工况

基于原子势能和半刚性结点梁单元应变能的等价关系来推导等效梁单元的参数。碳碳键的键长变化势能Ur、键扭转变化势能Uτ、键角变化势能Uθ分别为：

(5)

(6)

(7)

半刚性结点梁单元的伸长应变能UA与纯扭转应变能UT分别为：

(8)

(9)

式(8)～式(9)中，E为杨氏模量，A为截面面积，G为切变模量，J为截面极惯性矩。因半刚性结点梁单元的UA、UT与刚性结点梁单元相应值一致，故令UA=Ur、UT=Uτ，则有：

(10)

(11)

在图4所示的半刚性结点梁单元纯弯曲工况中，两端弹簧和中间杆件为串联连接，弹簧所受弯矩与杆件所受弯矩相同，皆为M，为了简化相关公式形式，令：

(12)

式中，I为截面惯性矩,则dθ1、dθ2与弯矩M的关系分别为：

(13)

(14)

梁单元结点的相对转角dθ与dθ1和dθ2的关系为：

dθ=dθ1+2dθ2

(15)

联立式(13)～式(15)可得：

(16)

中间杆件的应变能UM1为：

(17)

将式(16)代入式(17)可得

(18)

两端弹簧的总应变能UM2为：

(19)

将式(16)代入式(19)可得：

(20)

半刚性结点梁单元应变能UM与中间杆件应变能UM1及两端弹簧应变能UM2的关系为：

UM=UM1+UM2

(21)

将式(18)、式(20)代入式(21)可得：

(22)

令Uθ=UM，联立式(7)和式(22)可得：

(23)

为便于讨论，定义半刚性系数λ为弹簧弯曲刚度与中间杆件弯曲刚度的比值，则有：

(24)

将式(24)代入式(23)可得：

(25)

再将式(25)代入式(24)，获得弹簧弯曲刚度k2与半刚性系数的关系为：

(26)

1.4 半刚性结点梁单元的刚度矩阵

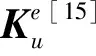
(27)

将式(10)代入式(27)可得：

(28)

(29)

将式(11)代入式(29)可得：

(30)

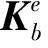
(31)

将式(24)与式(26)代入式(31)可得：

(32)

将以上推导所得半刚性结点梁单元的拉伸刚度矩阵(式(28))、扭转刚度矩阵(式(30))及弯曲刚度矩阵(式(32))合并，即可获得该梁单元的单元刚度矩阵。

2 石墨烯动力特性方程

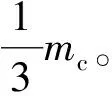
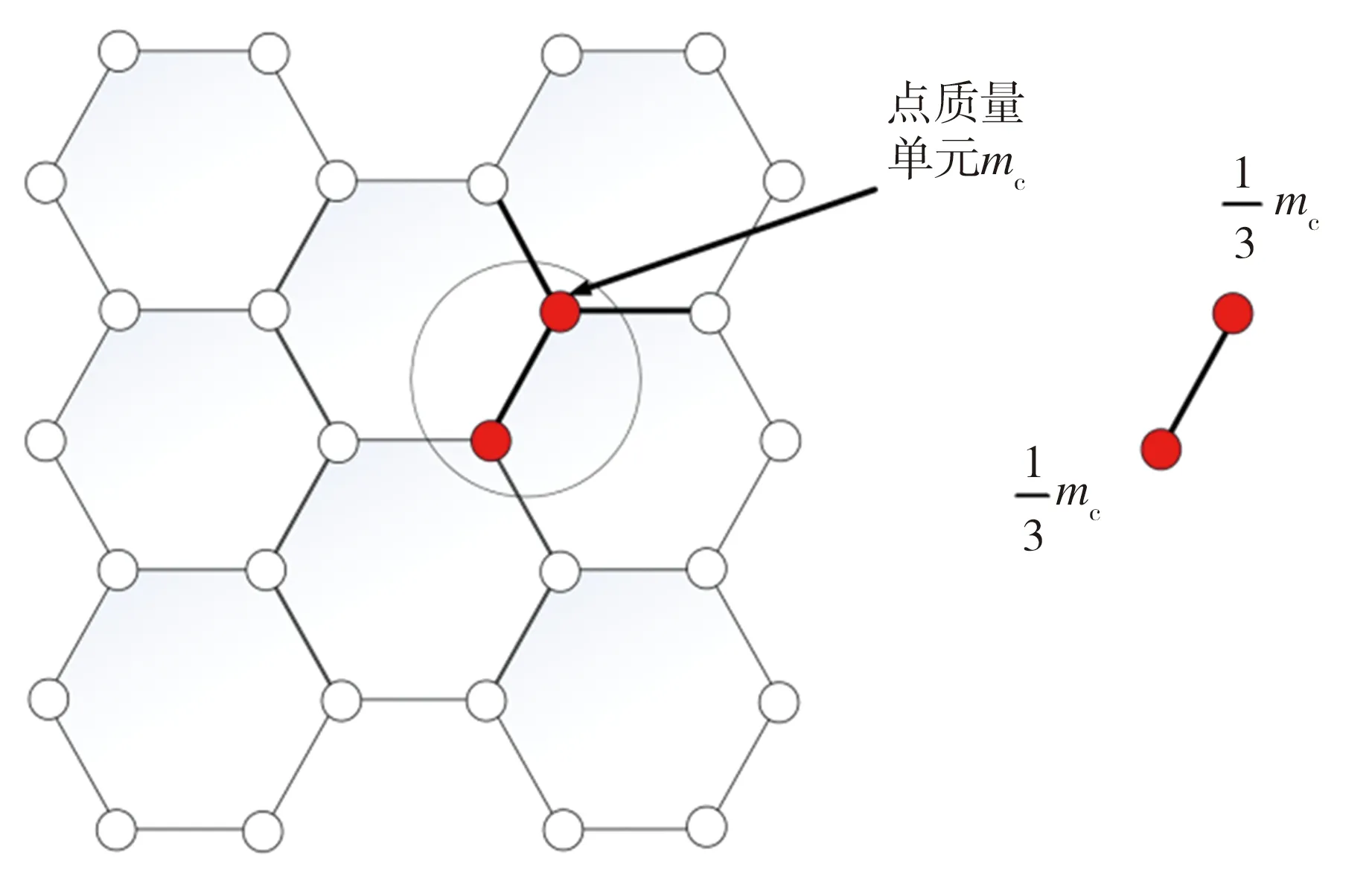
图5 点质量分配示意图

单元质量矩阵为集中质量矩阵，其分块矩阵形式为：

(33)

式中，M为单元质量矩阵Me集成所得整体质量矩阵，M11、M22为：

(34)

对石墨烯杆件结构模型进行模态分析，该结构自由振动方程[15]为：

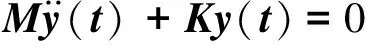
(35)

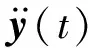
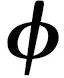
(36)

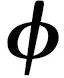
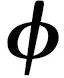
(37)

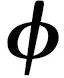
3 石墨烯动力特性分析

为了方便建模，在本文算例的石墨烯有限元模型中均将1个碳碳键划分为1个梁单元，边界条件皆设置为固支以模拟碳原子被固定。根据半刚性结点梁单元刚度矩阵和单元质量矩阵编写用户单元子程序UEL，基于ABAQUS平台运行子程序来计算石墨烯杆件模型的固有频率及受力变形，在有限元计算中所用有关参数见表1。

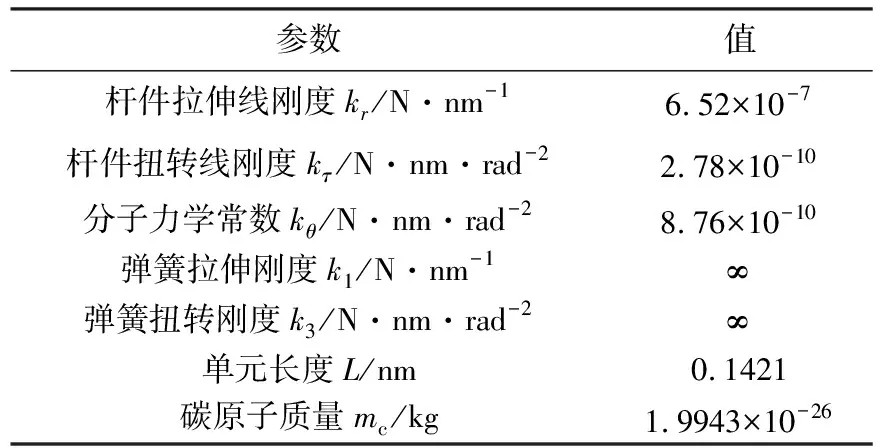
表1 有限元计算的力学参数

3.1 半刚性系数λ的确定

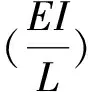
选取的石墨烯尺寸为10 nm×10 nm，其单向拉伸示意如图6所示,手性为扶手椅型，在y轴方向上的一组对边中，约束其中一个边界的y轴方向位移，而另一个边界则施加沿y轴正方向的位移0.1 nm，使其对应的拉应变ε为0.01。提取约束端所有结点的支座反力合力RF后利用胡克公式计算杨氏模量，胡克公式为：

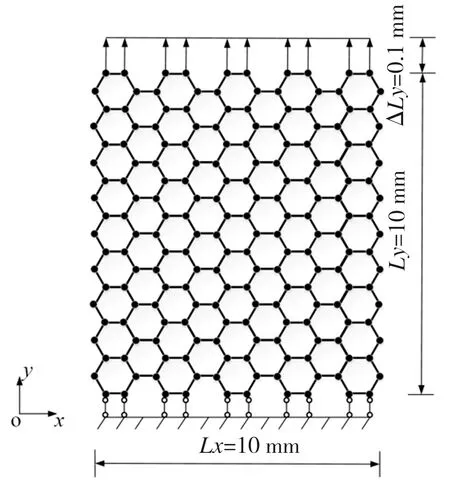
图6 石墨烯单向拉伸

(38)

式中，σ表示应力，ε表示应变，二者的计算公式分别为：

(39)

(40)

式(39)～式(40)中，Lx表示石墨烯x方向的尺寸，Ly表示石墨烯y方向的尺寸，ΔL表示边界端位移，h表示石墨烯的厚度，取0.34 nm。

首先将λ在0到∞之间取值，然后通过ABAQUS得到有限元计算结果，再代入式(38)～式(40)求解出石墨烯的杨氏模量，结果见表2。

表2 λ对杨氏模量计算结果的影响

表3所列为已有文献所报道的石墨烯杨氏模量值。由表3可见，理想石墨烯的杨氏模量实验值及模拟值均在1.0 TPa左右，而本研究利用半刚性结点杆件模型在λ取值为50时计算所得石墨烯杨氏模量值为1012 GPa(表2)，比较接近理想石墨烯的实验值和模拟值，因此后文算例中半刚性结点杆件模型的半刚性系数λ取值皆为50。

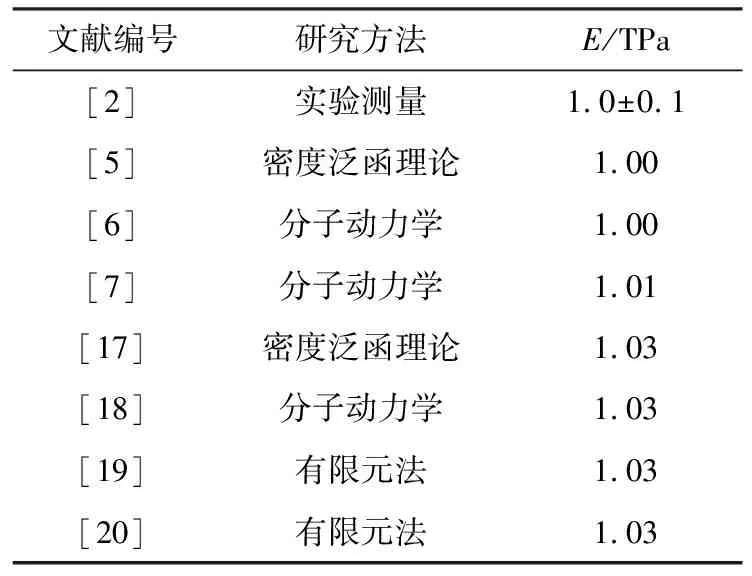
表3 石墨烯杨氏模量

3.2 手性的影响

为了研究手性对石墨烯固有频率的影响，选取相同尺寸、相同边界的扶手椅型和锯齿型两种手性石墨烯(见图(7))进行研究。石墨烯尺寸为10 nm×10 nm，边界条件皆为两边固定。

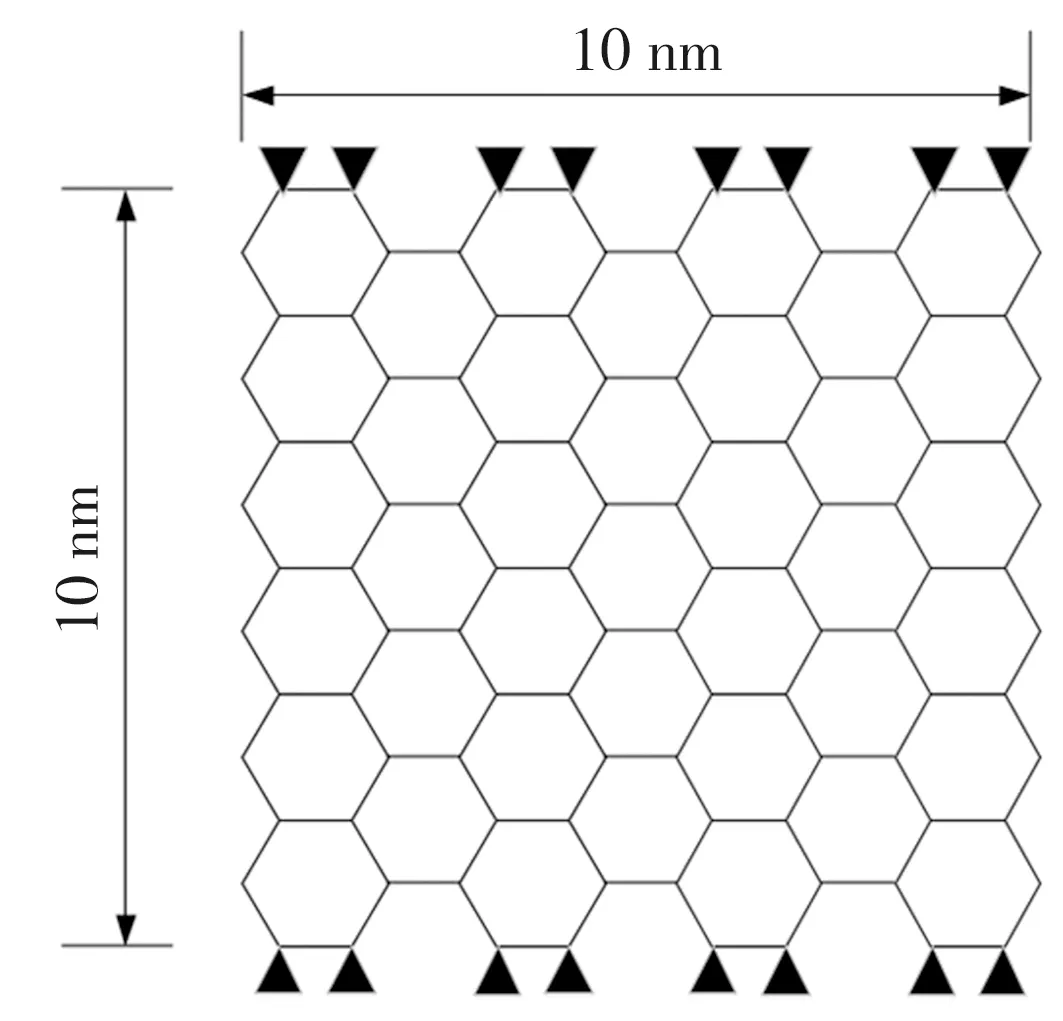
(a)扶手椅型石墨烯

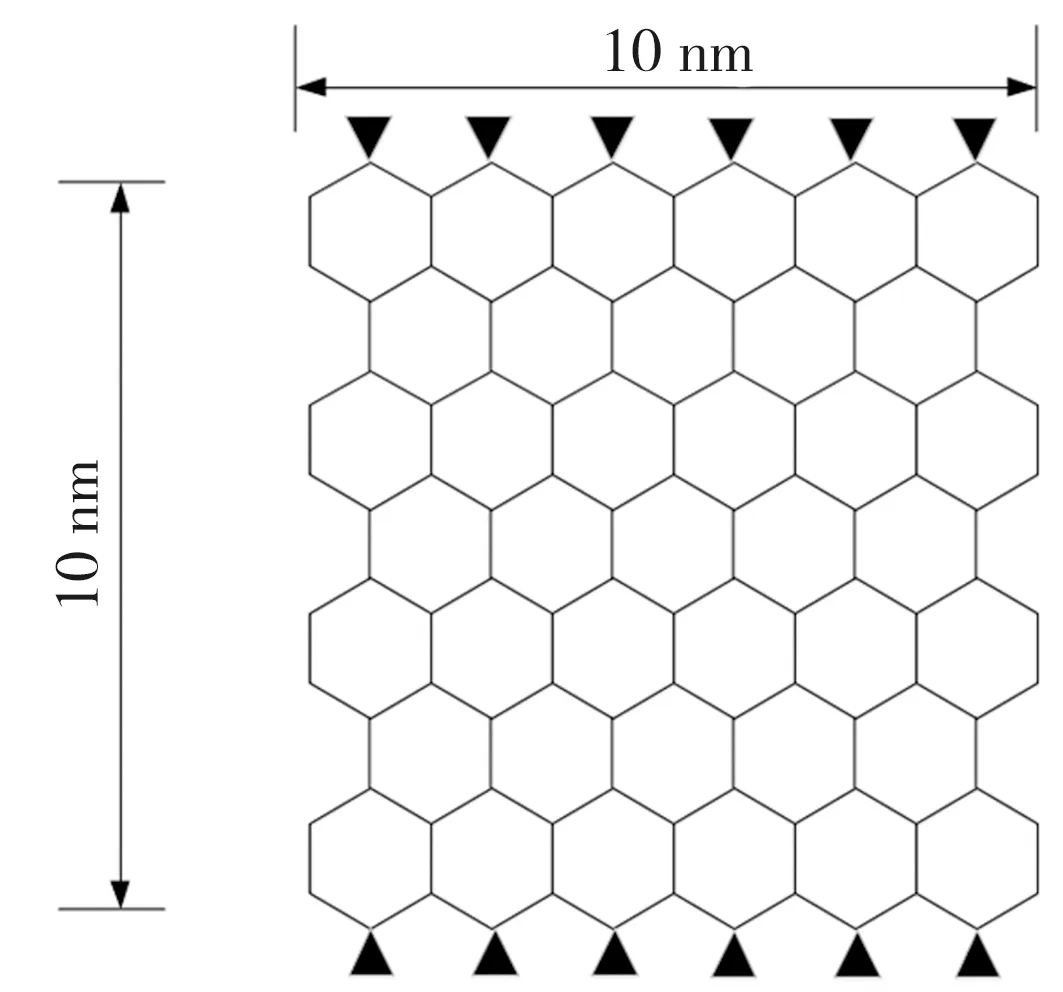
(b)锯齿型石墨烯

定义扶手椅型石墨烯与锯齿型石墨烯固有频率的偏差Δωa-ωz为：

(41)

式中，ωa表示扶手椅型石墨烯的固有频率，ωz表示锯齿型石墨烯的固有频率。通过计算获得不同手性石墨烯固有频率随固有频率阶数变化的曲线如图8所示，前5阶固有频率以及相应偏差的具体计算结果列于表4。结合图8和表4可以看出，扶手椅型与锯齿型石墨烯的固有频率曲线变化曲线几乎重合，二者前5阶固有频率值相差不大但扶手椅型石墨烯相应值略高，两种手性石墨烯的固有频率在第5阶的偏差最大，不过该偏差最大值也仅为 0.73%，这表明当石墨烯尺寸较大时，手性对石墨烯固有频率的影响不明显。

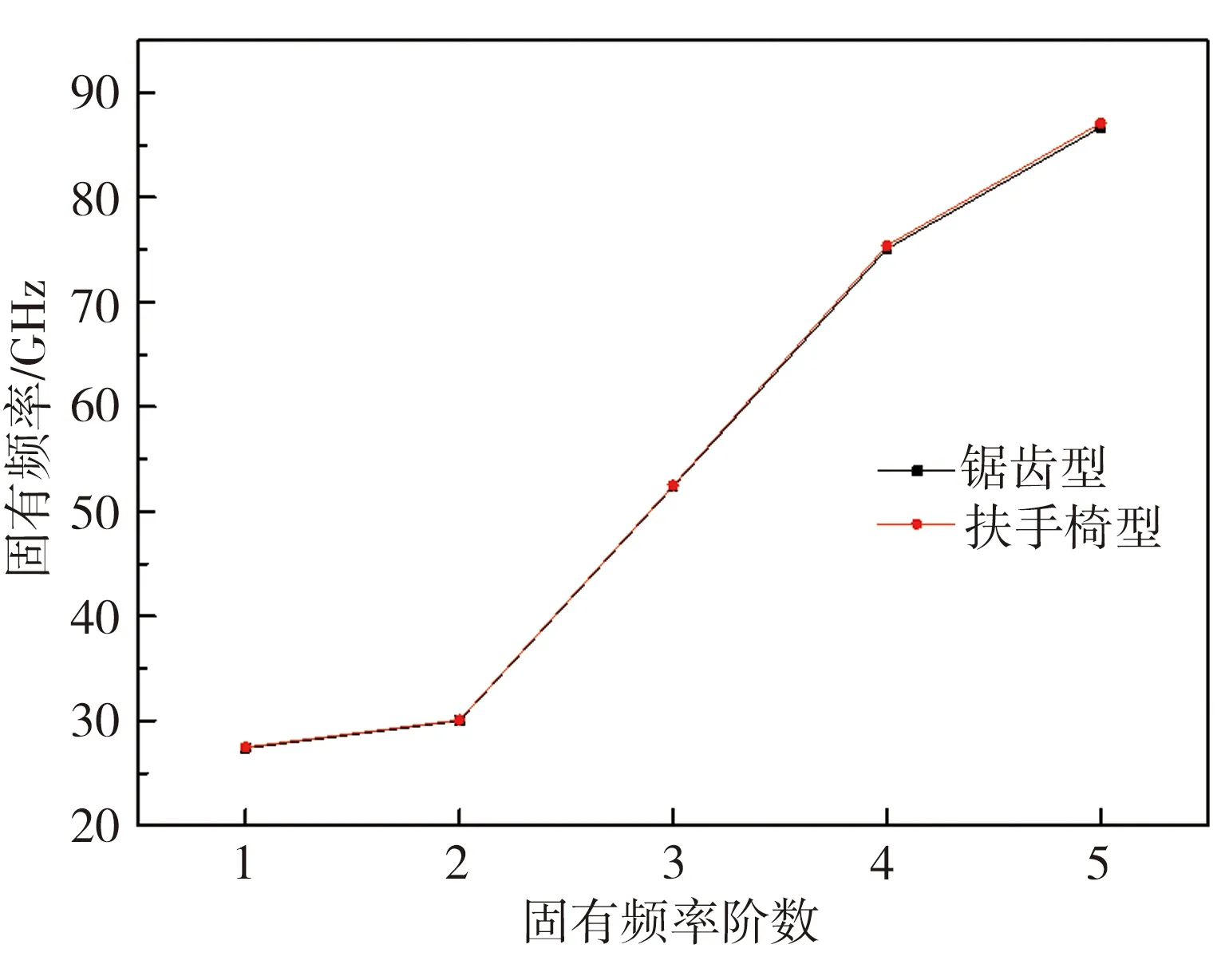
图8 固有频率变化曲线

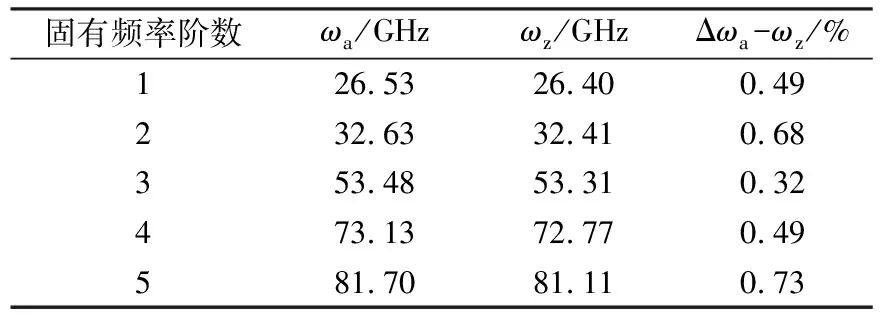
表4 不同手性石墨烯的前5阶固有频率

3.3 边界条件的影响

由3.2节可知手性对石墨烯前5阶固有频率几乎没有影响，故本文以尺寸相同、边界条件不同的扶手椅型石墨烯(见图(9))为考察对象来研究边界条件对石墨烯固有频率的影响。经计算，石墨烯前5阶固有频率随其固支边界数目的变化情况如图10所示。由图10可知，对于同一阶频率，石墨烯固有频率随固支边界数量的增多而增大。

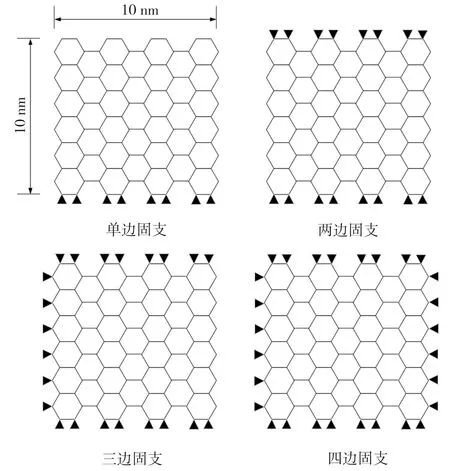
图9 不同边界条件下的扶手椅型石墨烯

为了进一步分析边界条件对石墨烯固有频率的影响，定义不同边界条件下石墨烯的频率增量为：

(42)

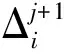
经计算所得不同边界条件下石墨烯前5阶固有频率以及同阶频率随边界约束数目增加而逐级变化的增量分别列于表5和表6。由表5和表6可知，当边界条件从单边固支变成两边固支(对边固支)时，石墨烯的前5阶固有频率均有明显增大，其中以第1阶固有频率的增量为最大，相应增幅高达539.28%，以第3阶固有频率增量为最小，相应增幅为105.81%；当边界条件从两边固支变成三边固支时，石墨烯的前5阶固有频率仍继续增大，但增幅相比其边界条件由单边固支变为两边固支时的相应值明显减小，此时以第2阶固有频率的增幅为最大(48.24%)，以第1阶固有频率的增幅为最小(9.01%)；当边界条件从三边固支变成四边固支时，石墨烯的前5阶固有频率又均有较明显的增大，其中第2阶固有频率的增幅最大(79.10%)，第3阶固有频率增幅最小(14.41%)。这表明将石墨烯的边界条件由单边固支变成两边固支时，能显著提升约束能力，因此石墨烯固有频率大幅增加，继续增加一条边界约束(三边固支)时，约束能力的提升程度受限，相应固有频率增幅明显减小，当边界条件为四边固支时，其约束能力又有较大的提升，此时固有频率增幅也相应增大。

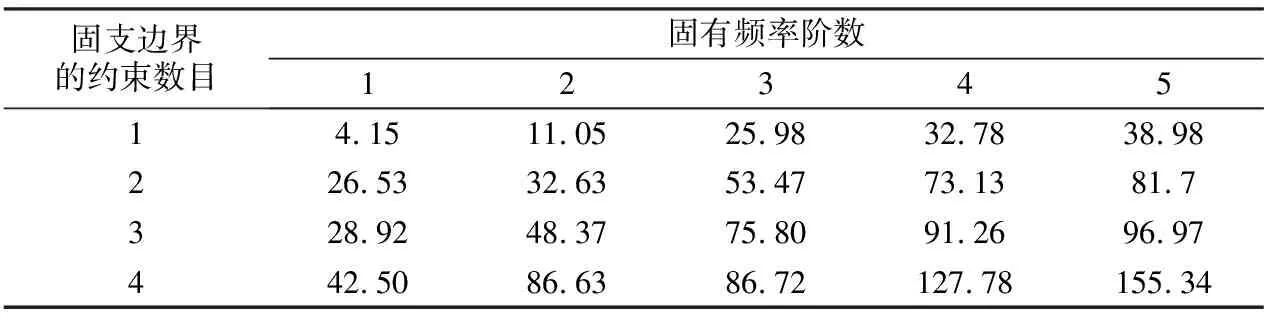
表5 不同边界条件下的固有频率(单位：GHz)

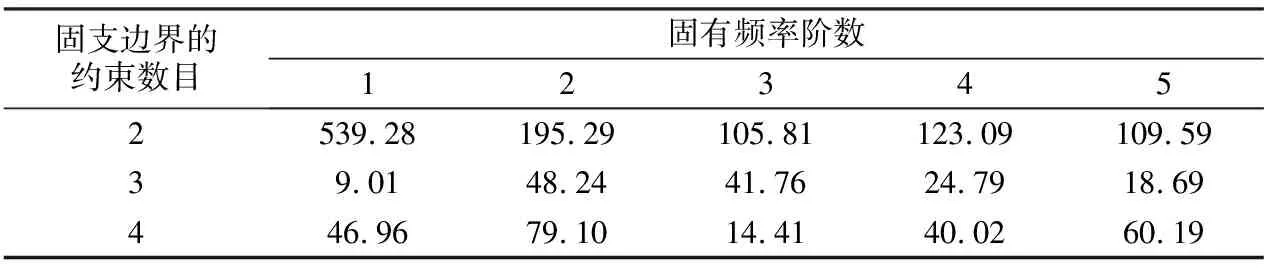
表6 不同边界条件下的频率增量(单位：%)

3.4 尺寸影响

以边界条件为两边固支的正方形扶手椅型石墨烯(见图(11))为考察对象来研究其边长l对其固有频率的影响，其中设定l分别为1、2、3、4、5、6、7、8、9、10、15、20、30、40、60、80 nm等16种工况。经计算，石墨烯各阶频率随l的变化如图12所示，具体计算结果列于表7。从图12中可以看出，石墨烯第1阶到第5阶的固有频率随尺寸l变化的规律基本一致，即随着石墨烯尺寸的增大，其各阶固有频率迅速减小。由表7可见，小尺寸石墨烯固有频率非常高，其中当l为1 nm时，相应石墨烯第1～5阶的固有频率依次达到2817.12、3311.82、4641.45、6857.53、7247.72 GHz；相比之下，大尺寸石墨烯的固有频率非常低，当l为80 nm时，相应石墨烯第1～5阶固有频率依次仅为0.42、0.52、0.85、1.16、1.29 GHz。此外，当l由1 nm增加至2 nm以及由2 nm继续增至3 nm时，石墨烯各阶固有频率在相应阶段均急剧减小，降幅显著，这表明石墨烯尺寸对其固有频率影响较大，存在明显的尺寸效应。

图11 正方形石墨烯

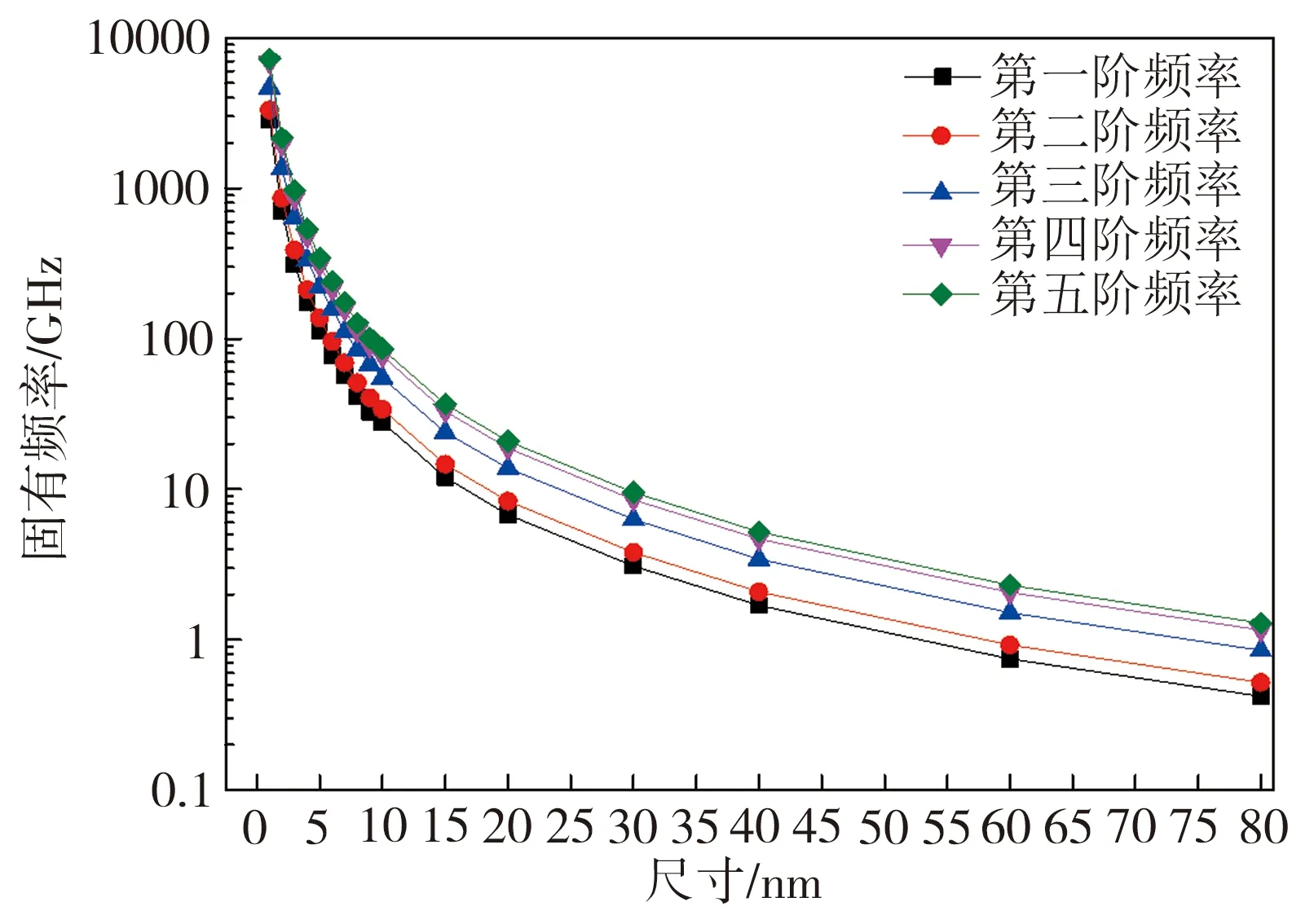
图12 尺寸对石墨烯固有频率的影响

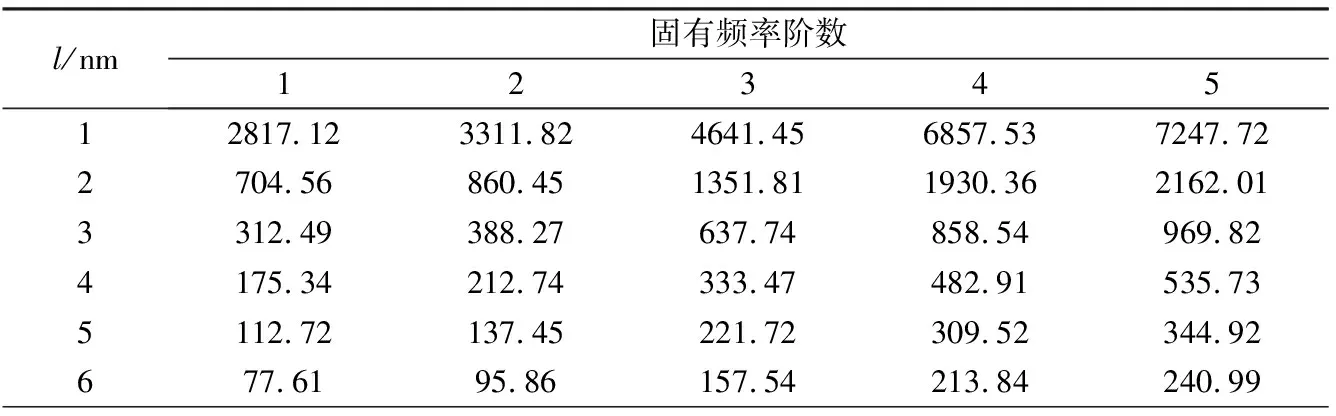
表7 不同尺寸石墨烯的前5阶固有频率(单位：GHz)

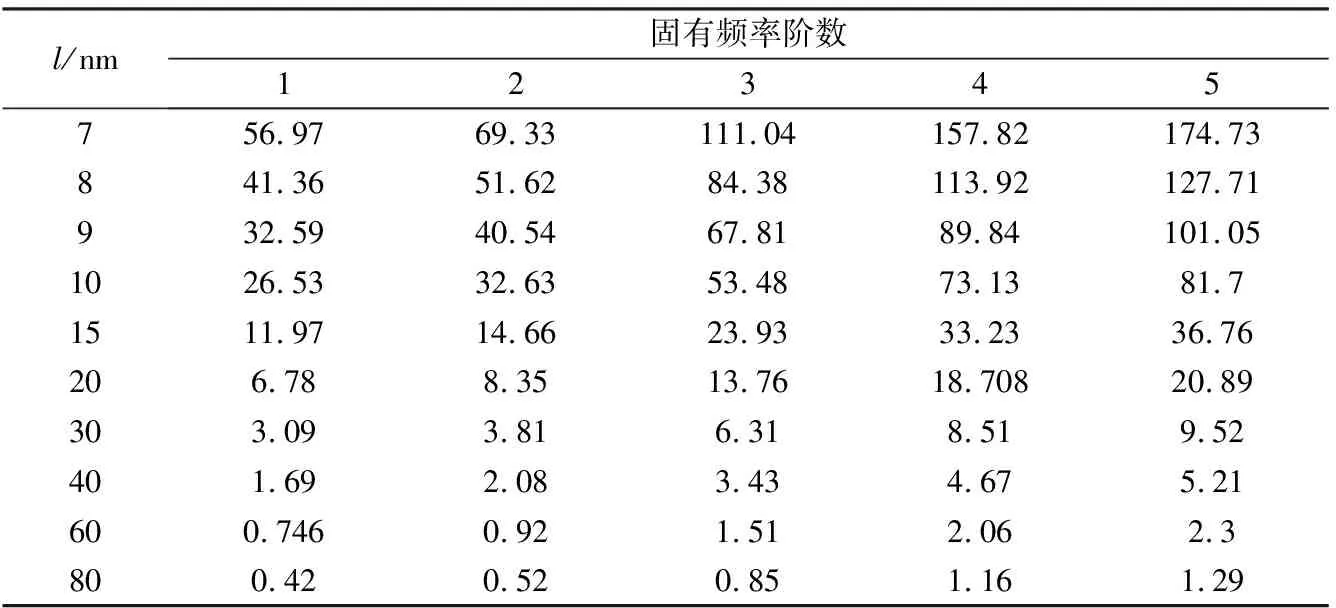
续表7

4 结语

本文针对石墨烯分子结构受力变形导致键角发生变化的现象，提出利用半刚性结点杆件模型来研究石墨烯的振动特性。首先以石墨烯的碳碳共价键为梁单元、碳原子为连接梁单元的半刚性结点，构建了模拟石墨烯结构的半刚性结点杆件有限元模型；然后采用分子力学的势能与半刚性结点梁单元应变能等效的方法获得半刚性结点梁单元参数与石墨烯分子力学常数的关系，并基于结构力学原理给出单元刚度矩阵，推导出石墨烯振动特性的求解方程；最后根据半刚性结点梁单元刚度矩阵及单元质量矩阵编写用户自定义子程序并借助ABAQUS平台运行子程序来研究石墨烯的振动特性，重点研究了石墨烯手性、边界条件以及尺寸大小对其固有频率的影响。数值算例表明，手性对石墨烯固有频率影响很小，边界约束数目的增多会显著提高石墨烯固有频率，而石墨烯的固有频率又随其尺寸的增大而减小。