考虑序列相关调整时间的多目标置换流水车间调度算法
姚 康,唐秋华,张子凯,蒙 凯
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
置换流水车间调度问题可描述为:n个工件在m台机器上顺序加工,各机器上的工件加工顺序恒定不变且每个工件在每台机器上只加工一次,目标是确定每台机器上工件的加工顺序及开工时间,使得特定的性能指标最优。这是一类经典的NP-hard问题[1],对该问题通常做如下假设:①一个工件在同一时刻只能在一台机器上加工;②在同一时刻,一台机器只能加工一个工件;③工件一旦在某台机器上进行加工就不能停止;④每台机器上工件的加工顺序相同。
传统研究认为,一台机器上相邻两个工件间的调整时间是可以忽略不计的,或者可与加工时间一起考虑。但是在印刷、纺织、化工和金属轧制等特定行业中,调整时间与加工序列相关且时间很长,必须单独考虑,以减少总调整时间,提高车间作业效率,因此对考虑序列相关调整时间的置换流水车间调度问题进行研究十分必要。
针对置换流水车间调度问题,张源等[2]以最大完工时间为目标,提出了一种改进粒子群算法,并引入NEH初始化方法和Metropolis准则;何启巍等[3]提出一种融合变邻域搜索的混合粒子群优化算法,同时优化最大完工时间和总流经时间,并验证了算法的有效性;汤可宗等[4]将中心引力优化算法和粒子群算法相结合,提出一种多策略粒子群优化算法,同时引入一种可引导粒子群体跳出局部最优解区域的集合变异方式,用来增强粒子群的全局搜索能力;陈可嘉等[5]针对最大完工时间和总延迟时间两个目标函数,设计了改进食物链算法,并将非支配排序融入其中,但是该算法并未考虑序列相关调整时间。针对考虑调整时间的置换流水车间调度问题,王建军等[6]提出一种改进的文化基因算法,并引入了干扰时间这一概念;Peng等[7]将变邻域搜索和遗传算法相结合,用以优化最大完工时间;Sioud等[8]提出一种改进的候鸟算法,并引入邻域搜索、禁忌搜索和重启机制。这几种方法在求解考虑调整时间的单目标置换流水车间调度问题时均取得较好的效果,但是不能直接用于相应的多目标置换流水车间的调度优化。
为此,针对考虑序列相关调整时间的多目标置换流水车间调度问题,本文设计一种基于非支配排序、带重启机制的多目标迭代贪婪(restarted multi-objective iterated greedy, RMIG)算法,用于同时优化最大完工时间(makespan)和总加权延迟(total weighted tardiness, TWT)[9]两个目标。该算法主要创新如下:①设计一种混合多种策略的启发式初始化方法,使得在算法初始阶段获得较优的初始外部归档集;②将非支配排序和贪婪操作相结合,以实现迭代贪婪算法从单目标向多目标的拓展;③设计一种适应问题规模和非支配解在解空间分布特点的重启机制,能够在算法进化到一定程度时扩展搜索广度。
1 问题模型
为便于对所求解的问题进行准确描述,引入如表1所示参数和变量。
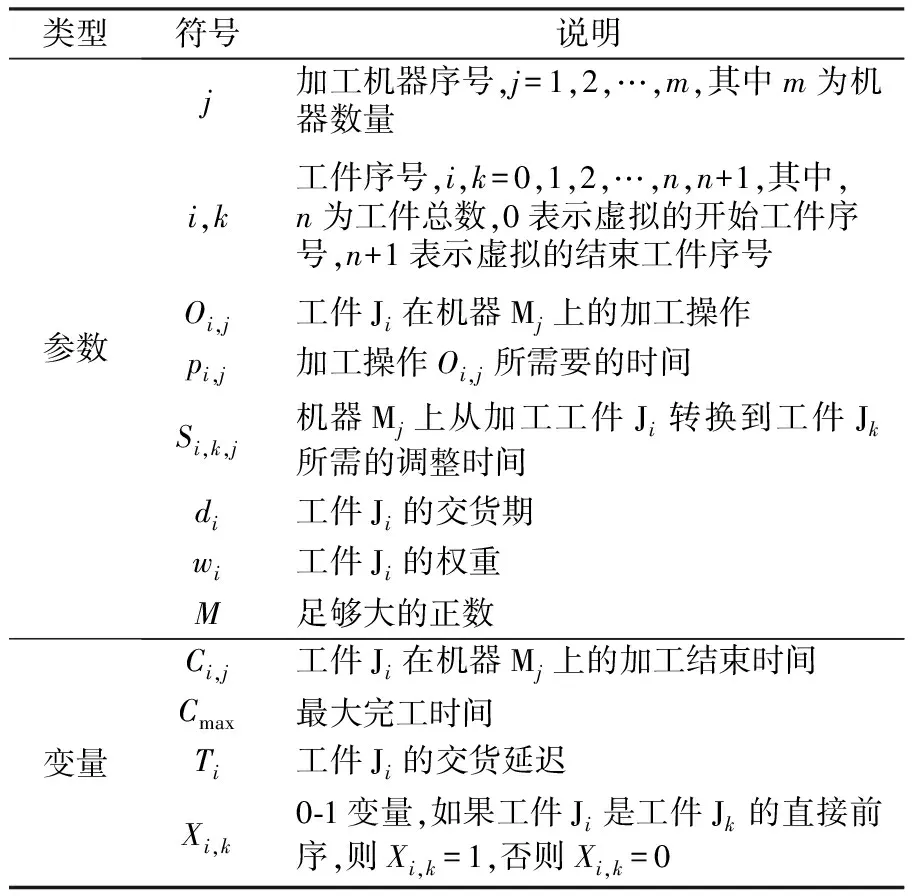
表1 符号及其说明
所求问题的数学模型为:
minf1=Cmax
(1)
(2)
(3)
(4)
Ck,j≥Ci,j+pk,j+Si,k,j-(1-Xi,k)M,
∀i,k,j,i≠k
(5)
Ck,j≥Ck,j-1+pk,j-(1-Xi,k)M,
∀i,k,i≠k,∀j∈{2,3,…,n}
(6)
Ck,1≥Ci,1+pk,1+Si,k,1+(Xi,k-1)M,
∀i,k
(7)
C0,j=0,∀j
(8)
Cmax≥Cn+1,m
(9)
Ti=max(Ci,m-di,0),∀i
(10)
Ci,j≥0,∀i,j
(11)
Xi,k∈{0,1},∀i,k,i≠k
(12)
式(1)~式(2)表示目标函数分别为最小化最大完工时间和最小化总加权延迟;式(3)保证除虚拟开始工件之外,每个工件有且只有一个直接前序,且虚拟结束工件不能作为直接前序;式(4)保证除虚拟结束工件之外,每个工件有且仅有一个直接后序;式(5)表示每道工序的加工结束时间要不早于其直接前序的加工结束时间加上该工序的操作时间和调整时间;式(6)~式(7)表示在同一台机器上,只有前一工件加工完成且进行机器切换后,才能加工后一工件;式(8)表示虚拟工件0的加工结束时间为0,因虚拟工件的加工操作所需时间为0,则其加工开始时间也为0;式(9)~式(10)定义了两个目标函数值的确定方法;式(11)定义了工件加工结束时间的取值范围;式(12)定义了二元决策变量。
2 带重启机制的多目标迭代贪婪算法
Ruiz等[10]最早将迭代贪婪算法应用于置换流水车间调度问题,取得了良好的效果。Minella等[11]又对该算法做出了改进,使其适用于多目标问题,但并未考虑序列相关调整时间。迭代贪婪算法主要分为初始化、破坏和重建三个部分,其算法思想为:通过NEH初始化得到一个初始解[12],从中随机截取d个单元,并得到一个部分序列;依次将截取出的每个单元插回到使得部分序列的目标函数值最小的位置中,重复d次后得到一个新解;重复上述破坏、重建过程,直至满足终止条件。考虑到所研究问题的多目标属性,本文在原始迭代贪婪算法的基础上引入一种混合多种策略的初始化方法,同时将重建和非支配排序相融合,最后设计出一种考虑解的分布性的重启机制。
2.1 混合三种策略的启发式初始化
算法设计时若仅采用针对某一个目标函数的初始化方法,会导致算法在初始阶段偏向于对该单一目标函数的优化。若采用基于多种策略的启发式初始化方法,可以在初始阶段生成一个分布性较好的外部归档集,在后续迭代过程中利用选择策略从归档集中挑选个体进行优化迭代。
为了在生成归档集时能够考虑到所有目标函数,同时又能够具有一定的互补性,本文采用了三种不同的启发式初始化方法:NEH、Rajendran等[13]提出的启发式方法(后文简称为“Ra”)以及融合NEH与最早交货期优先准则(earliest due date,EDD)的启发式方法(NEH_EDD)。NEH和Ra是分别针对最大完工时间和总延迟的两种经典初始化方法。NEH_EDD基于NEH的思想,同时考虑到工件交货期和相应的权重,具体步骤如下,其中TWTb表示当前最小总加权延迟。

Input工件集合J,工件交货期dj,权值wj,s=Ø根据dj/wj的值对工件进行升序排列,得到J=(J1, J2,…,Jn)for i=1 to n TWTb=∞ for k=1 to i 将工件Ji插入到s的第k个位置上; 计算每一个部分解s的TWTk; if TWTk 如果基于初始解直接构造外部归档集,某些初始解可能会在算法进化前期就已从归档集中被剔除。初始解的丢失会影响解空间的拓展,导致在某一个目标函数对应方向上的搜索力度不足。因此在采用NEH、NEH_EDD和Ra方法生成三个不同的解之后,再对这些初始解进行贪婪操作,用生成的非支配解集作为初始归档集。 在传统的迭代贪婪算法中,破坏过程会对一个完整可行解依次随机截取d个单元,重建过程每次也只保留当前最优解。对于多目标问题,非支配排序是判别个体之间优劣关系的重要手段。非支配排序的概念是:对于两个可行解s1和s2,若一部分目标k满足fk(s1)≤fk(s2),且∃k使得fk(s1) 第一步:破坏阶段。从一个长度为n的完整可行解中随机取出d个连续工件,得到一个长度为n-d的部分序列sp; 第二步:重建阶段。将取出的d个工件逐个重新插入sp中。第i次进行重组时会得到n-d+i个部分序列,保留这些序列中的非支配个体进行后续的重建。重复插入过程d次,直至得到完整可行解。 贪婪操作的具体示例如下: 图1 贪婪操作示例 相比于传统的迭代贪婪算法,RMIG在破坏阶段和重建阶段都做出了改进。在破坏阶段,RMIG取长度为d的连续工件集,不再是逐个取出。对于归档集中一个性能较好的非支配解,有些工件的紧前或紧后工件可能存在着相对较好的组合,尤其是加工时长较大的工件和加工时长较小的工件组合固定搭配时,能够保证解的质量在不断迭代过程中不会发生较大程度的劣化。破坏阶段随机选取d个连续的工件,能够在一定程度上避免这种劣化,同时还能加快算法的运行速度。在重建阶段,RMIG和非支配排序相融合,每次保留非支配部分序列进行后续的重建。新的重建方式既保留了迭代贪婪算法的核心思想,又很好地迎合了多目标问题的特性。 为了使归档集中的非支配解在解空间中有更好的分布,在归档集连续经过δ次迭代却没有更新的时候,对算法进行重启。设定参数δ=n/2,随着问题规模的增大,该迭代次数也将增加,可实现重启次数与问题规模之间的折衷。 传统的重启方式多为随机生成一个新的可行解来代替当前解,但是当算法运行一定时间后,随机生成的个体很难更新归档集。为了更好地发挥重启机制的作用,从归档集中选取距离之和d(si)最大的个体来代替当前个体进行迭代,以改善非支配解在解空间的分布性。 综上,本文在传统迭代贪婪算法的基础上进行改进,设计了一种启发式多目标迭代贪婪算法,其中,非支配排序起到了至关重要的作用,最主要的目的是舍弃受支配的个体,保留非支配解进行后续迭代,从而保持了算法的高效性,同时又能保证搜索不会向着个体劣化的方向进行。RMIG算法的具体流程如下: 输入: d, ND=Ø,δ输出: 非支配解集NDND初始化归档集(NEH, NEH_EDD, Ra)Counter=0while不满足终止条件 while Counter ≤δ s1选择(ND) sp,sR破坏(s1) s2重建(sp,sR) 融合非支配排序 ND_temp非支配排序(s3∪ND) if ND_temp∪ND-ND= Ø then Counter←Counter+1 else Counter=0 end if ND←ND_temp end while s1重启, Counter=0end while 对RMIG算法性能进行测试,并与已有文献中的部分经典算法进行比较,对比算法包括异质种群多目标遗传算法(multi-objective genetic algorithm with heterogeneous populations,hMGA)、多目标模拟退火算法(multi-objective simulated-annealing algorithm, MOSA)、改进食物链算法(improved food chain algorithm, IFCA)和帕累托迭代贪婪算法(iterated Pareto greedy, IPG)[10]。测试案例源于文献[10],工件数×机器数的组合为{20,50}×{5,20}以及{50,100}×{10},每个组合中包含5个案例,共30个算例。 所有算法均使用MATLAB语言编写,并在CPU为Intel(R) Core(TM) i5-4440 3.10 GHz的计算机上进行测试。算法的停止准则为最大运行时间T=m·n·150 ms。每个算例独立运行10次,取评价指标的平均值作为实验结果。 使用Hypervolume(记为IH)[15]和Unary Epsilon(记为Iε)[9]这两种常用指标对解的质量进行评估。对于两个目标函数最小化问题,IH为每个非支配解所独立支配区域的面积之和,计算时要先对目标函数值进行标准化处理,即将其映射到区间[0,1],初始参照点选取(1.2,1.2),因此IH极限值为1.44。IH指标是对解的分布性的综合评估,与非支配解集对帕累托真实前沿的接近程度成正相关,指标值越大表明解的分布性越好。Iε用来衡量已经获得的帕累托前沿和真实帕累托前沿的最小距离,该指标的计算方式如下: (13) 式中:P为帕累托真实前沿或某个参照集合;S为算法求得的非劣解集;χ1和χ2分别为解集S和P中的非支配可行解。Iε指标值一般介于1和2 之间,Iε越趋近于1,表明所获得的帕累托前沿与真实前沿越接近。 RMIG算法有两个参数需要确定,分别为破坏数d和重启参数δ,本文采用田口实验进行参数校验。d取3个水平值(5,10,15);δ取3个水平值(n/2,n,2n)。采用IH来比较所获得的解,在信噪比上选择望大特性,根据实验结果(见图2),确定d和δ分别取5和n/2。 图2 RMIG参数的信噪比主效应图 其他对比算法的参数校验同样采用田口实验方法,具体结果如表2所示,其中MOSA算法中x的取值决定了算法在本次迭代过程中优化哪一个目标函数。 表2 参数校验结果 本文算法主要的改进措施包括混合多种策略的启发式初始化方法和考虑解的分布性的重启机制。为了验证改进算子的有效性,将不加入改进算子、只加入启发式初始化方法、同时加入启发式初始化方法及重启机制的3种多目标迭代贪婪算法(分别命名为IG、IG+initial、IG+initial+restart)进行比较,采用IH和Iε两个指标来衡量算法性能。对前述30个算例各独立运行10次的指标均值进行统计,得到如图3所示95%置信区间。 实验结果显示,两种改进算子对算法性能均有提升,且考虑分布性的重启机制的改进效果更为明显。采用混合多种策略的启发式初始化方法,在算法进化初期能够保证优化方向不是偏向某一个目标函数,而是在两个不同的目标函数之间取得平衡。考虑分布性的重启机制能够大幅提升算法性能的原因在于:①重启参数与问题规模相适应,重启机制能够根据问题的不同规模在适当的时机发挥作用,使得算法在同一块解空间搜索过度时转换搜索方向;②重启机制与选择机制互补,选择机制偏向于选择归档集中距离和最小的个体进行下一次迭代,而重启机制则选取归档集中距离和最大的个体进行下一次迭代,这无疑扩大了算法搜索的广度。 (a) IH均值的95%置信区间 (b)Iε均值的95%置信区间 为了测试算法整体性能,运用本文算法和对比算法求解前述30个算例,每个算例运行10次得到的指标均值见表3,其中较好的结果用粗体显示。 表3中的实验结果显示,从IH指标来看,RMIG在所有算例上都展现出最优性能;从Iε指标来看,RMIG也在大多数算例上有最好的表现; 表3 不同算法的运行结果对比 续表3 同时,当问题规模越大时,RMIG的性能优势越明显。综上所述,本文提出的RMIG算法在整体性能上要优于4种对比算法。 本文针对实际生产中经常出现的带有调整时间的多目标置换流水车间调度问题,提出了一种基于非支配排序的迭代贪婪算法RMIG。针对多目标问题设计了有效的启发式初始化方法,根据非支配解在解空间中的分布特点设计了具有互补性的选择和重启机制。采用多个不同规模的标准案例对提出的改进算子进行了有效性验证,同时证明了本文算法在性能上优于对比算法。未来可考虑将该算法应用到类似于分布式置换流水车间调度这样更加切合实际的工程问题中。2.2 选择
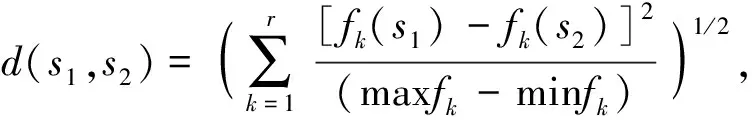
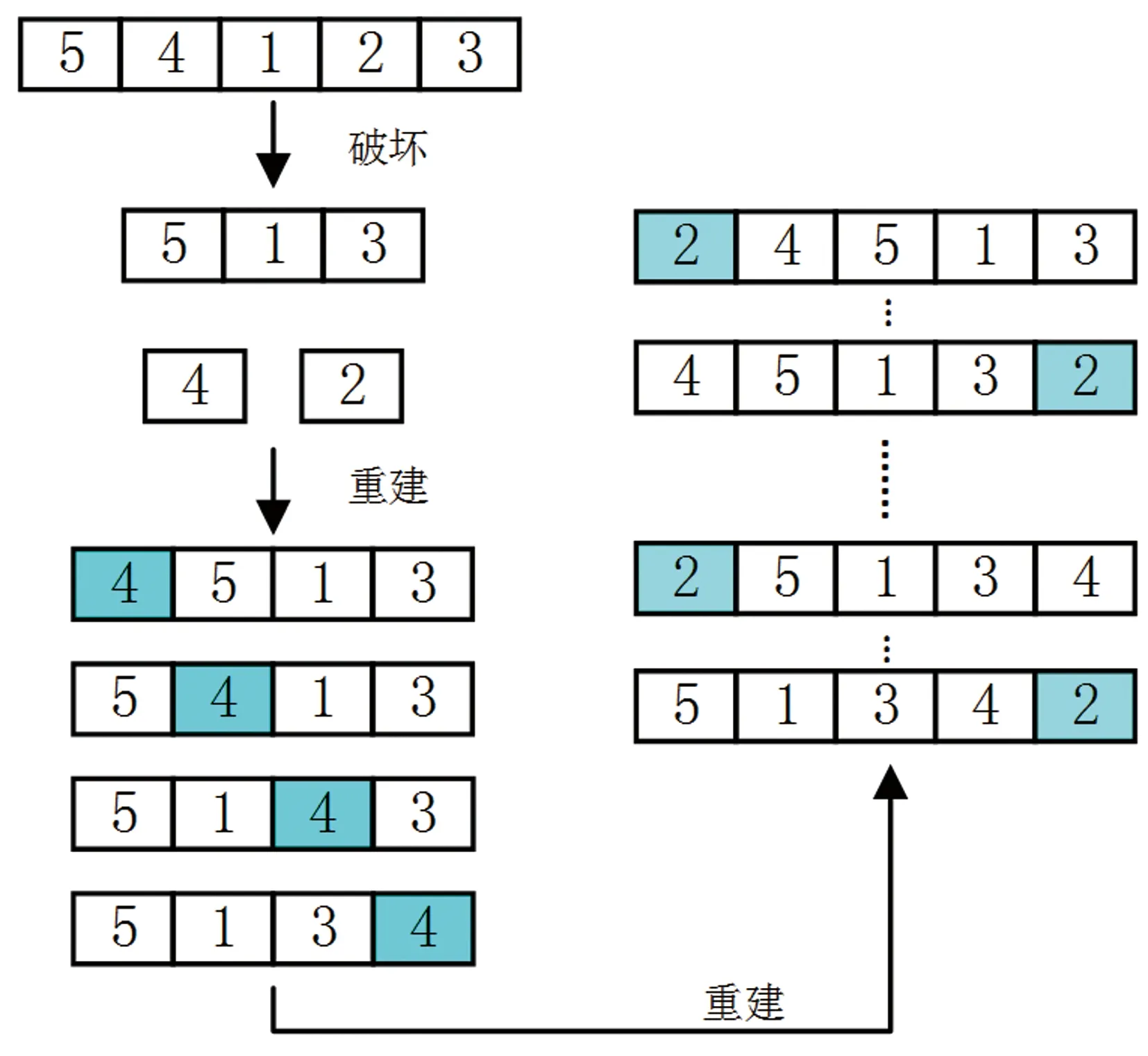
2.3 基于非支配排序的贪婪操作
2.4 考虑解的分布性的重启机制
2.5 RMIG算法流程

3 实验结果和分析
3.1 评价指标
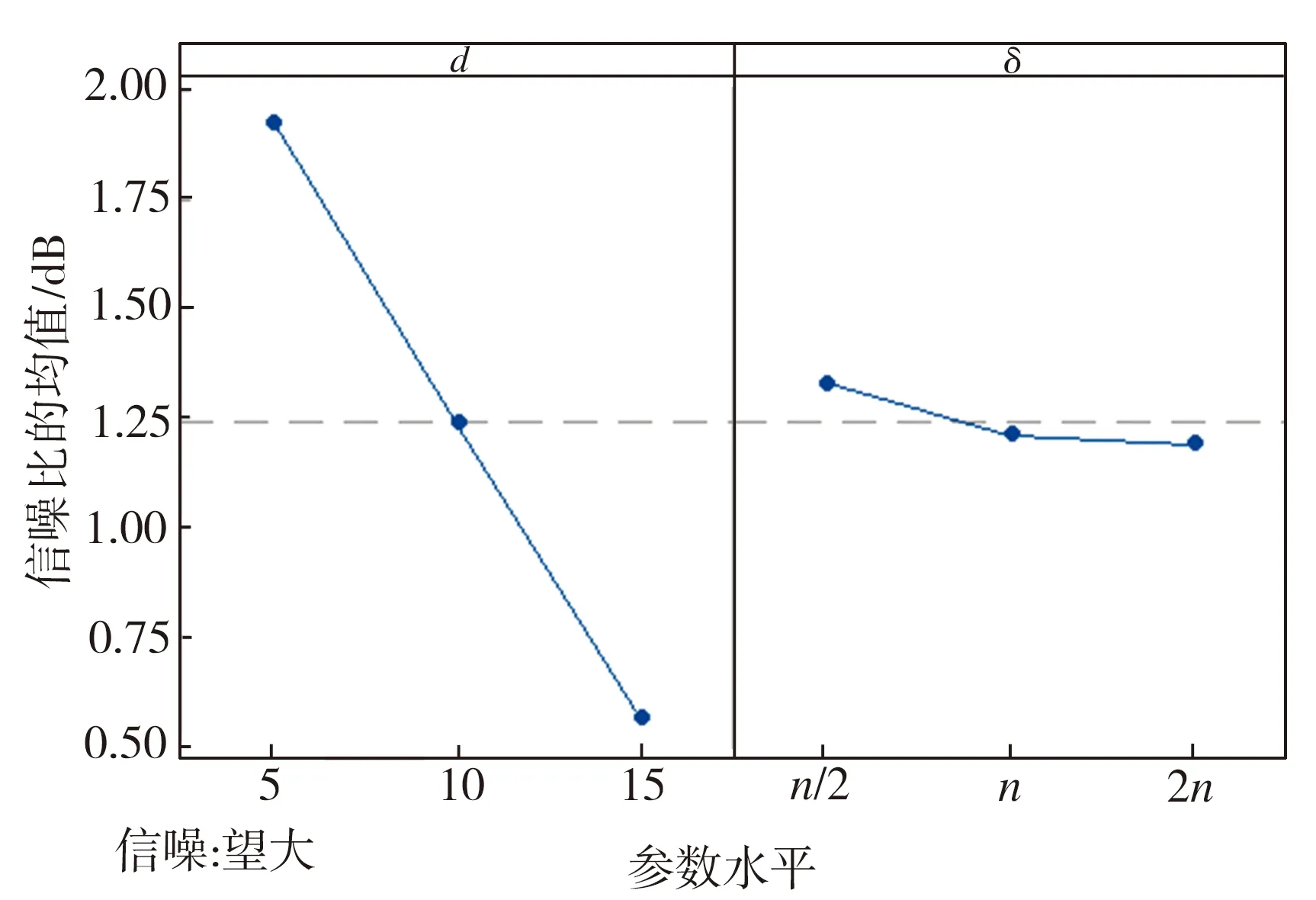
3.2 参数校验
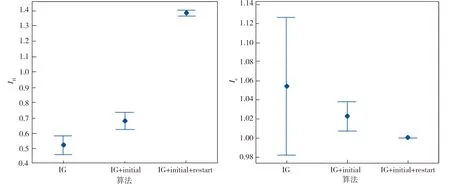
3.3 改进措施效果分析
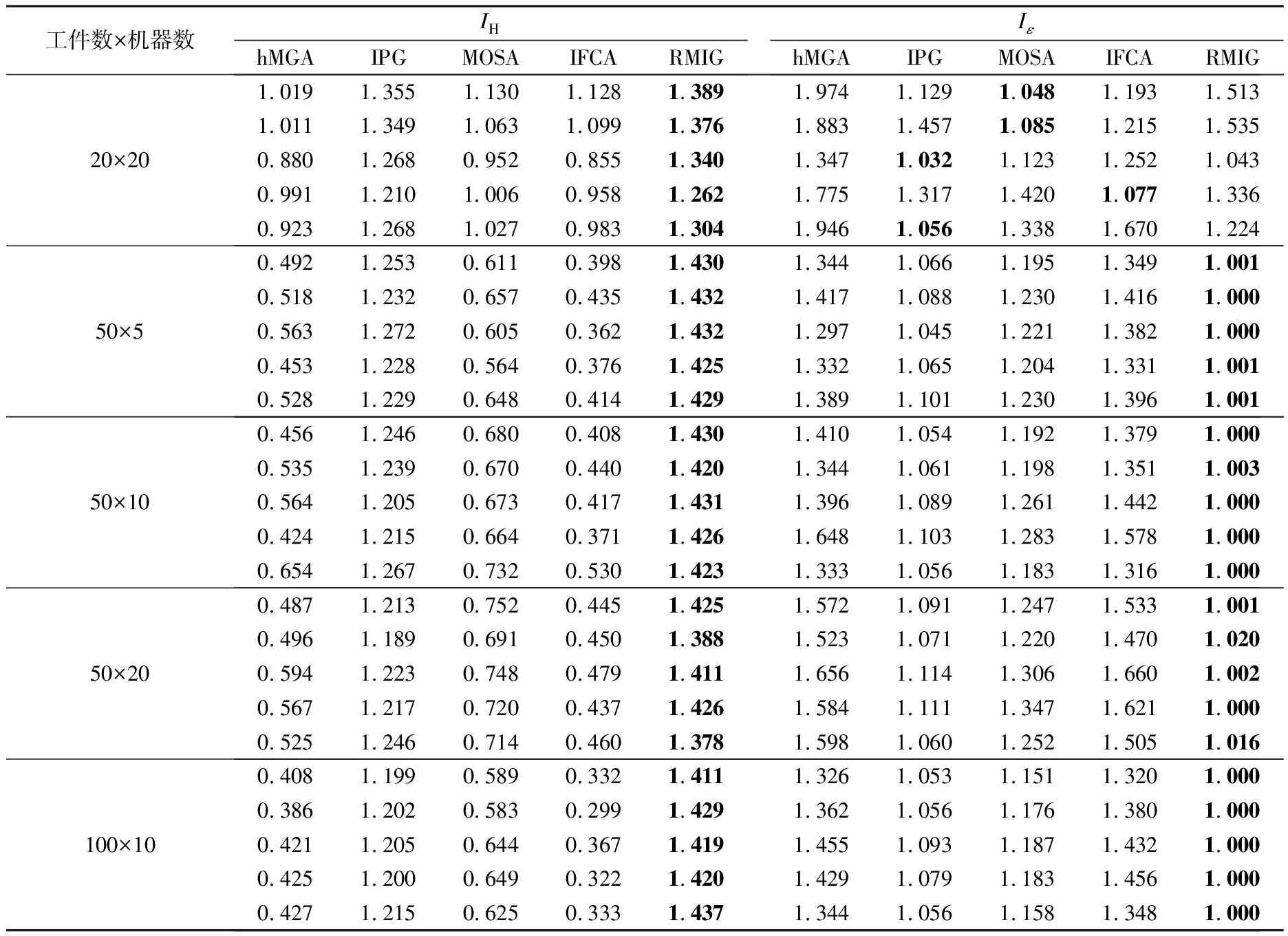
3.4 算法对比

4 结语

