一种自适应共振解调方法及其在铁路轴承故障诊断中的应用

刘文朋，杨绍普，李 强，刘永强，顾晓辉

（1.北京交通大学 机械与电子控制工程学院，北京 100044；2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043）

为了自适应地识别共振频带，Antoni[4]创造性地提出了谱峭度理论和快速峭度图方法，受到了广泛的关注。之后，基于谱峭度原理[5-6]，众多学者相继提出了一系列的改进方法用来确定最佳的共振频带。一方面，为了提高分解效果，开发了更精确的带通滤波器（如小波包[7-8]、双树小波[9-10]、Morlet小波[11]、动态贝叶斯小波变换[12]等）；另一方面，采用更稳健的指标来衡量滤波信号的脉冲性（如平滑指数[13]、基尼系数[14]、L2/L1准则[15-16]、负熵[17]等）。以上方法虽然取得了一定的效果，但对通带内的噪声却无能为力，当故障处于早期或者通带内噪声水平较高，将会对上述方法产生极大地干扰。针对带内噪声干扰问题，文献[18-19]通过利用流形学习方法进一步对轴承微弱故障特征增强，均取得了不错的效果。近期，Moshrefzadeh等[20]提出了一种共振解调的新方法，该方法充分利用了轴承故障信号的二阶循环平稳性，计算了解调信号的平方包络的无偏自相关，而非解调信号的峭度，取得了良好的效果。该方法的主要优点是，通过对每个解调频带的自相关处理进一步增强了故障冲击的强度，从而降低了非周期脉冲和噪声对解调频带的影响，提高了算法的检测能力。然而，随着研究的深入，发现该方法易受到复杂干扰的影响，当测试轴承处于一个相对平稳的工况时，Autogram能够寻找到最优的频带，而随着运行环境的恶化，寻找到的共振频带往往趋向于低频带，该方法的有效性逐渐降低。而在实际的工程中，轴承的运行环境往往比较恶劣，例如高铁轴承会受到变载荷和轮轨激励等复杂工况的影响。因此，发展一种稳定性好，能够适应复杂工况的共振解调方法，更能满足工程实际应用的需要。

本文提出了一种新的自适应的共振解调方法，通过最大重叠离散小波包变换将原始信号分解到不同的尺度，以滤波后平方包络信号自相关谱的峭度值作为度量指标，代替Autogram方法中滤波后平方包络信号的自相关的峭度值，生成一种新的峭度图。在自相关谱中，故障特征频率的周期性得到了更好的保持，抗干扰的能力更强。最后，通过不同工况下的高铁轴承实验信号和铁路货车早期故障轴承实验信号验证了该方法的有效性。

1 基本原理

1.1 最大重叠离散小波包变换[21]

为了更好地介绍最大重叠离散小波包变换（maximal overlap discrete wavelet packet transform，MODWPT），首先简要介绍了最大重叠离散小波变换（maximal overlap discrete wavelet transform，MODWT）。可以看作是离散小波包变换（discrete wavelet transform，DWT）的改进版本，它是一种高冗余非正交小波变换，对样本长度N没有严格的要求。 这里，{gl，l=0，1，…，L-1}和{hl，l=0，1，…，L-1}为DWT的低通滤波器和高通滤波器，L为滤波器的长度。

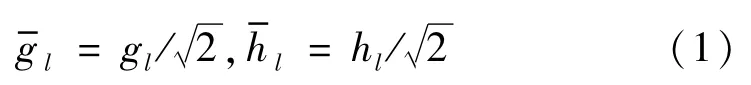
式中，gl和hl满足如下等式约束。

为了克服由于降采样过程造成的信号数据在每一分解层上各半点的缺点，利用MODWT方法在{gl}和{hl}中插入2j-1个零，在不同的第j层上重建了一个新的滤波器。

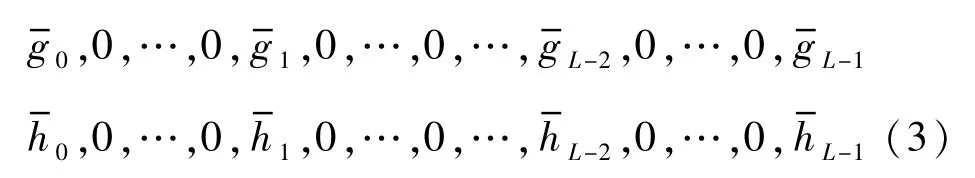
基于Mallat算法，MODWT的第j级尺度变换系数V′j，t和小波变换系数W′j，t分别为

离散小波包变换可以弥补离散小波包变换不能进一步分解高频带的缺点。为了同时对信号的高频段进行分解，类似与由DWT方法导出的DWPT，提出了基于MODWT的MODWPT方法。该MODWPT不仅具有MODWT的所有优点，而且可以分解高频带。MODWPT系数Wj，n可计算为

针对本组PHC患者，采用多因素逐步Cox比例风险回归模型对影响患者生存率的危险因素进行统计分析，变量赋值见表4。结果表明，术前较差的肝功能、较低的组织分化程度、门静脉侵犯、出现淋巴结转移、较高的TNM分期和高表达Pim-1蛋白是影响PHC患者生存时间的独立危险因素；而性别、年龄、肿瘤数目、肿瘤直径和术前血清AFP含量与患者总体生存期无关(表5)。

式中:j为分解层；n为每个层下的频带数。

1.2 无偏自相关

无偏自相关（auto-correlation，AC）定义如式（6）所示

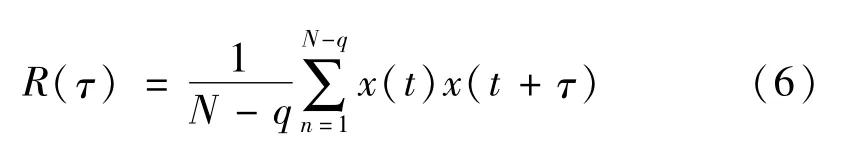
式中:x（t）为时域信号；τ=q/fs为延迟因子，fs为采样频率；q=0，1，2，3，…，N-1。

根据式（6）可知，随着τ的增加，用来计算AC的数据样本数量将会逐渐减少，因此后面得到的结果没有足够的估计方差。因此，只有部分计算的AC被保留用于进一步的计算。

1.3 峭度指标

峭度是度量数据尖峰的一种统计指标，因此可以用来检测与旋转机械相关的信号中的故障冲击信息强弱。峭度的定义为

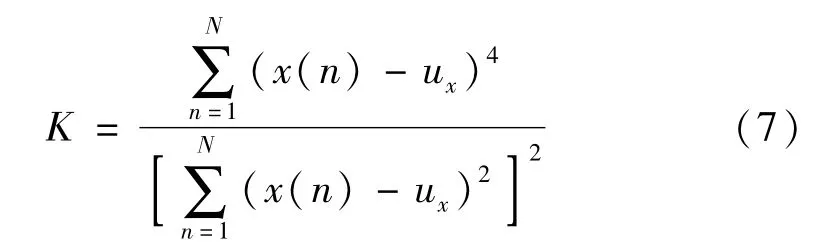
式中:x（n）为时域信号；ux为均值；N为数据的长度。

2 自适应的共振解调方法

传统的峭度图方法，如快速峭度图方法，通过计算滤波信号的包络的峭度表征冲击的强弱，在信噪比较高的情况下，应用快速峭度图方法一般可以准确地找到故障轴承最佳的共振频带，但在故障冲击不明显或信号中存在高峰值的脉冲干扰时，该方法有效性和稳定性大大降低。主要是因为峭度指标，能够很好地刻画故障信号的冲击性而无法表征故障冲击的循环平稳性。Wang等提出的Autogram方法，对滤波信号进行自相关处理，计算了平方包络信号自相关的峭度，进一步降低了带内噪声的干扰，但是当轴承处于复杂工况的时候，即使通过自相关处理，仍然会存在一些较强的干扰成分，影响算法的有效性。然而，在自相关谱中，故障特征频率的周期性得到了更好的保持，抗干扰的能力更强，因此可以通过峭度指标评价自相关谱中故障特征频率的稀疏性，从而识别最佳的共振频带。基于此，提出了一种更为鲁棒的自适应共振解调新方法。具体的操作流程如下所示:

步骤1通过MODWPT将原始信号分解到尺度K，分解为中心频率fc=（i+2-1）*2-k-1和带宽Nw=2-k-1的子带信号Ck，i（n） （k为峭度图的尺度，k=0，1，2，…，K，Ck，i（n）为第i个子带信号），如图1所示。 为了保证频带内拥有足够的故障相关信息，以最底层的带宽不小于3倍的轴承内圈故障特征频率为原则选取最大的尺度K。

图1 当K=3时的峭度图分解方式Fig.1 The kurtogram decomposition mode when K=3

步骤2首先对每个子带滤波信号的平方包络进行自相关处理，然后进行傅里叶变换，得到自相关谱。

步骤3计算每个子带对应自相关谱的峭度，并选取最大峭度对应的频带作为最优频带进行滤波，各频带自相关谱的峭度的计算方式如式（8）所示。

式中，SAC（n）为由步骤2得到的自相关谱信号。

步骤4对步骤3选取的滤波信号进行平方包络谱分析，从而诊断故障类型。

3 高铁轴承故障诊断分析

为了验证该方法的有效性，将其应用于高铁轮对轴承，轴承型号为FAG-80781109。试验轴承外圈有人为加工的局部缺陷，宽度约为1 mm，长度约为5 mm，深度约为0.7 mm。轴承结构参数如表1所示。通过高铁轴承试验台采集了空载、静载和动载三种不同工况下的振动信号。静载工况下，测试轴承径向静载力设为85 kN，轴向设为50 kN。动载荷工况是为了模拟轮对轴承工作过程中的载荷变化，在垂直方向施加随机激励，平均力约为80 kN，频率范围为0.2～20 Hz。在轴向施加频率为0.2～20 Hz，最大为50 kN的随机激励。动载力如图2所示。

表1 轴承参数Tab.1 Bearing parameters

图2 动态加载力Fig.2 Dynamic loading force

基本实验设置如图3所示。实验时，转速设定为2 100 r/min，相对应高铁运行的速度大约350 km/h，采样频率为51 200 Hz，应用振动加速度传感器采集3 s的数据，三种工况下的故障信号时域波形如图4所示，在三种工况下包络谱图中，仅在空载状态下的识别了外圈故障频率三倍频。根据轴承尺寸和转速，计算得到轴承的外圈故障特征频率fo、内圈故障特征频率fi、滚动体故障特征频率fb分别为255.5 Hz，339.5 Hz和119.7 Hz。

图3 试验台及故障轴承Fig.3 Test bench and faulty bearing

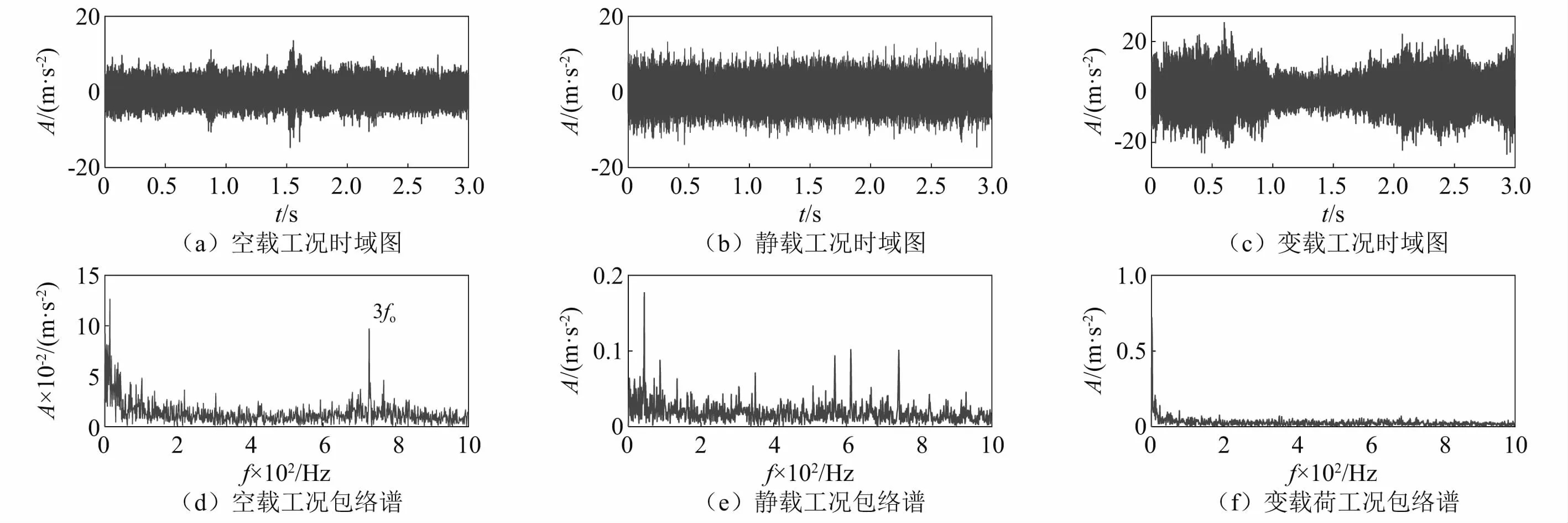
图4 振动信号时域图及其包络谱Fig.4 Time-domain waveform of vibration signal and its envelope spectrum

3.1 空载工况下故障诊断分析

首先，采用本文所提方法对空载工况下采集的振动信号进行分析，并和Autogram方法分析结果对比。两种方法所得的峭度图如图5所示。由图5（a）可知，Autogram确定的共振频带的中心频率为16 000 Hz、带宽为6 400 Hz。由图5（b）可知，本文所提方法确定的共振频带的中心频率为18 000 Hz、带宽为800 Hz。根据Autogram方法确定的共振频带和本文所提方法确定的共振频带，分别进行带通滤波和平方包络谱分析，结果如图6和图7所示。通过对比可知，在图6（a）和图7（a）中均可以观察到比较明显的冲击信息，在图6（b）和图7（b）的平方包络谱中均找到了故障特征频率及其二、三、四倍频，诊断效果相当，证明了本文方法的有效性。

图5 空载工况下峭度图Fig.5 The kurtogram under no-load condition

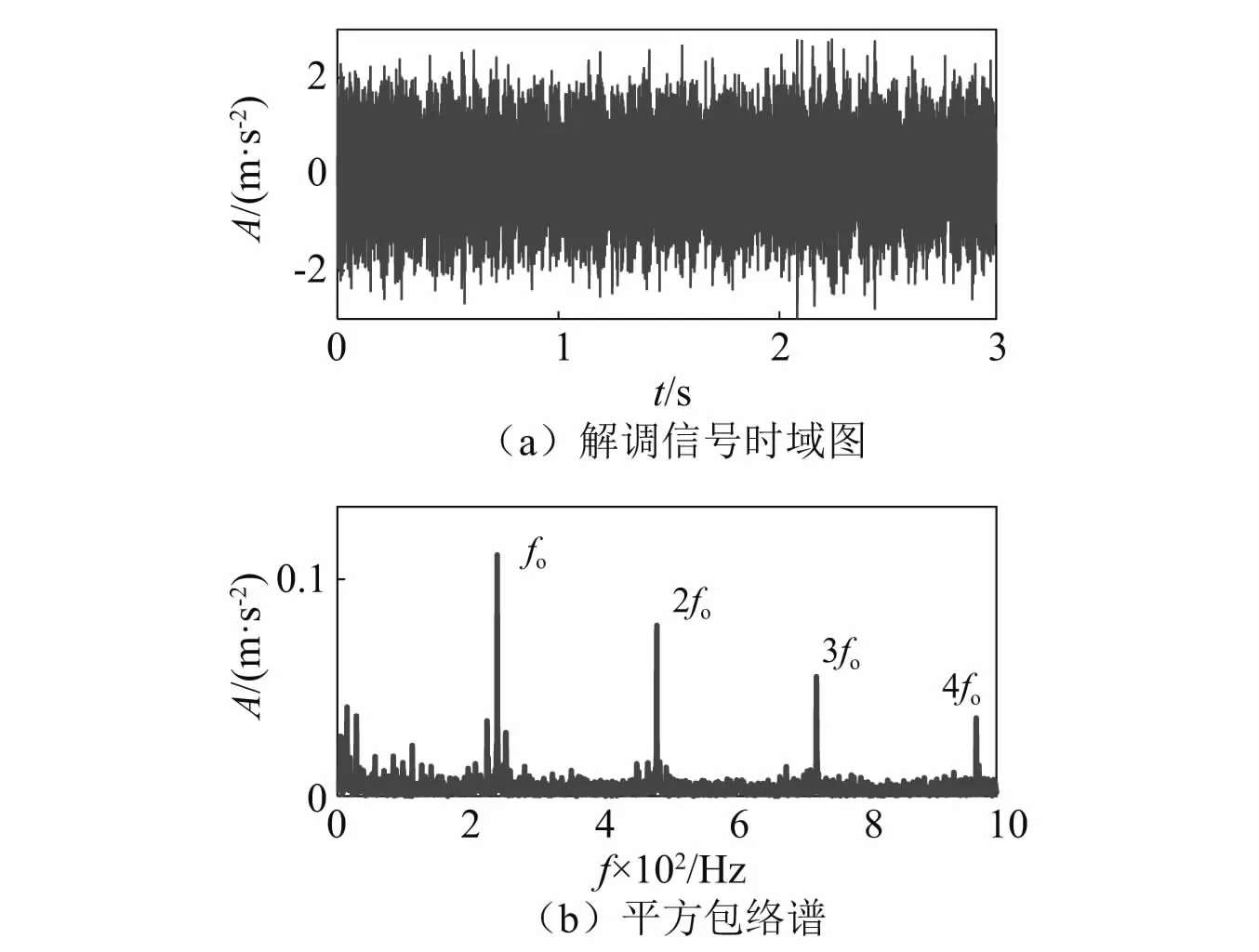
图6 空载工况下Autogram方法分析结果Fig.6 The results of Autogram method in this paper under no-load condition

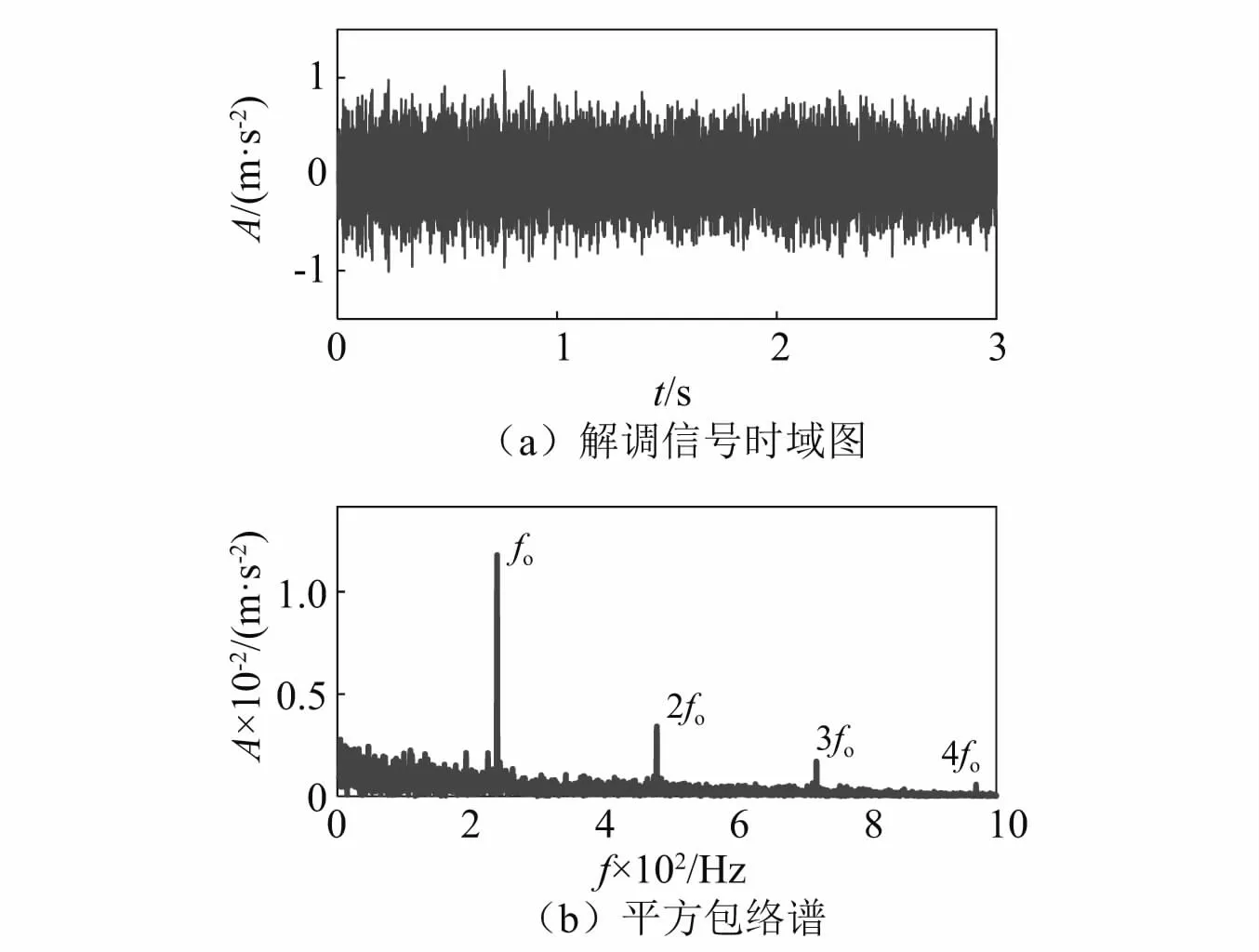
图7 空载工况下本文所提方法分析结果Fig.7 The results of the proposed method in this paper under no-load condition

3.2 静载工况下故障诊断分析

采用本文所提方法对静载工况下采集的振动信号进行分析，并和Autogram方法分析结果对比。两种方法所得的峭度图如图8所示。由图8（a）可知，Autogram确定的共振频带的中心频率为2 800 Hz、带宽为800 Hz。由图8（b）可知，本文所提方法确定的共振频带的中心频率为10 000 Hz、带宽为800 Hz。根据Auto-gram方法确定的共振频带进行带通滤波和平方包络谱分析，结果如图9所示。图9（a）中可发现两个比较明显的大脉冲，图9（b）中观察到了比较明显的故障特征频率，故障频率倍频均被背景噪声频率淹没。根据本文方法所确定的共振频带进行带通滤波和平方包络谱分析，结果如图10所示。图10（a）中故障冲击明显，图10（b）中观察到了比较明显的故障特征频率及其二倍频、三倍频。通过对比可知，两种方法虽然能够诊断轴承发生外圈故障，但本文方法所确定的共振频带包含更多的轴承故障信息，体现了本文方法的优越性。

图8 静载工况下峭度图Fig.8 The kurtogram under static load condition

图9 静载工况下Autogram方法分析结果Fig.9 The results of Autogram method in this paper under static load condition

图10 静载工况下本文所提方法分析结果Fig.10 The results of the proposed method under static-load condition

3.3 变载荷工况下故障诊断分析

采用本文所提方法对静载工况下采集的振动信号进行分析，并和Autogram方法分析结果对比。两种方法所得的峭度图如图11所示。由图11（a）可知，Autogram确定的共振频带的中心频率为400 Hz、带宽为800 Hz，因此在本节例子中Autogram寻找到的共振频带为一个低频带。由图11（b）可知，本文所提方法确定的共振频带的中心频率为15 200 Hz、带宽为1 600 Hz。根据Autogram方法确定的共振频带进行带通滤波和平方包络谱分析，结果如图12所示。图12（a）中可发现滤波信号幅值波动比较剧烈，图12（b）中故障频率几乎被背景噪声频率淹没，难以确定轴承是否发生故障。根据本文方法所确定的共振频带进行带通滤波和平方包络谱分析，结果如图13所示。图13（a）中故障冲击明显并伴有较明显的幅值波动，图13（b）中观察到了比较明显的故障特征频率及其二倍频、三倍频、四倍频和五倍频。通过对比可知，通过本文方法所确定的共振频带能够确定轴承发生外圈故障，而Autogram方法无法识别是否发生故障。

图11 变载工况下峭度图Fig.11 The kurtogram under variable load condition

图12 变载荷工况下Autogram方法分析结果Fig.12 The results of Autogram method under variable load condition

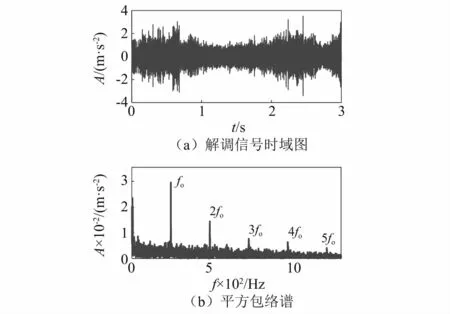
图13 变载荷工况下本文所提方法分析结果Fig.13 The results of the proposed method under variable load condition

4 铁路货车轴承故障诊断分析

为了进一步验证本文方法的有效性，选取了在服役过程中自然产生缺陷的轮对轴承，并采用如图14所示的货车轮对轴承跑合实验台验证了诊断效果。测试轴承型号为197 726，在外圈滚道出现了较轻微的凹坑，轴承参数如表2所示。

图14 轮对轴承跑合实验台及故障轴承Fig.14 The test bench of wheel set bearing and the fault bearin g

表2 轴承参数Tab.2 Bearing parameters

实验时，设定转速为465 r/min，采样频率为25 600 Hz，采集4 s的数据，故障信号的时域波形及包络谱如图15所示。根据轴承参数，可以计算得到轴承的外圈故障特征频率fo、内圈故障特征频率fi、滚动体故障特征频率fb分别为66.7 Hz，88.3 Hz和27.1 Hz。

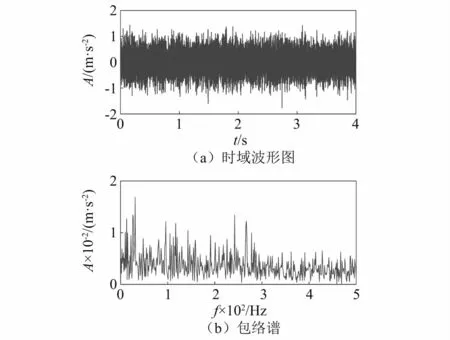
图15 故障轴承振动信号Fig.15 The vibration signal of fault bearing

采用本文所提方法采集的振动信号进行分析，并和Autogram方法分析结果对比。两种方法所得的峭度图如图16所示。由图16（a）可知，Autogram确定的共振频带的中心频率为7 400 Hz、带宽为400 Hz，因此在本节例子中Autogram寻找到的共振频带为一个低频带。由图16（b）可知，本文所提方法确定的共振频带的中心频率为5 200 Hz、带宽为800 Hz。根据Autogram方法确定的共振频带进行带通滤波和平方包络谱分析，结果如图17所示。图17（b）中可以观察到外圈故障特征频率几乎被复杂的干扰频率淹没，难以确定轴承是否发生故障。根据本文方法所确定的共振频带进行带通滤波和平方包络谱分析，结果如图18所示。图18（b）中观察到了比较明显的外圈故障特征频率。通过对比可知，通过本文方法所确定的共振频带包含更多的故障信息。

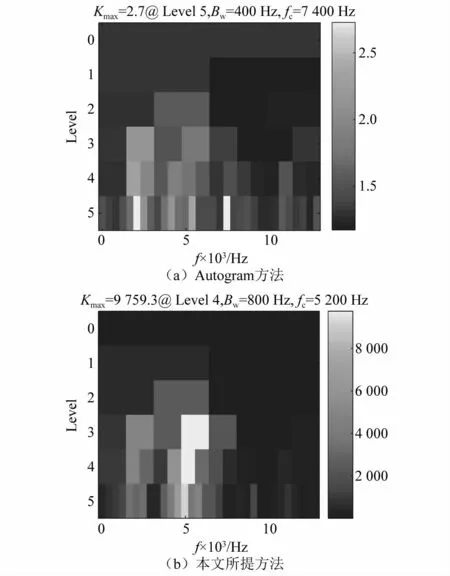
图16 峭度图Fig.16 The kurtogram

图17 Autogram方法分析结果Fig.17 The results of Autogram method

图18 本文所提方法分析结果Fig.18 The results of the proposed method

5 结 论

本文提出了一种基于自相关谱峭度图的自适应共振解调新方法，并通过高铁轴承和铁路货车轴承实验信号证明了该方法的有效性，并与Autogram方法进行了对比。Autogram仅在空载、静载的工况下识别了轴承故障，未能识别变载荷工况下的轴承故障，而本文方法在空载、静载荷和变载荷工况下都能有效识别故障轴承的类型，且在静载和变载荷工况下的结果均优于Autogram方法，从而验证了本方法在复杂的监测环境中对干扰成分具有更高的鲁棒性，能更为精准的识别滚动轴承最优解调频带，具有较高的工程应用价值。