基于VMD-RQA的直线振动筛激振力不平衡故障诊断

范 伟，何越宙，王 寅，陈 华

（1.华侨大学 机电及自动化学院，福建 厦门 361021；2.福建南方路面机械有限公司，福建 泉州 362021）

随着我国工业化的不断进程，振动筛分机械设备已在矿山、建筑、冶金、化工等行业中起到不可或缺的作用。直线振动筛[1]作为一种典型的振动筛分机械设备，由激振器、筛箱、弹簧减振装置、支承底架以及传动装置等组成，筛箱利用激振器所产生的动力在强交变载荷下受迫振动。由于激振器长期的高速旋转和强振动作业，激振器中的零部件会发生故障，例如轴承磨损、偏心快移位等问题。在实际生产中，激振器是封闭的，无法在里面布置传感器得到振动信息，当发生明显的轴承磨损、偏心快移位时，激振器作用力发生变化，筛箱两侧对称点的振幅差不满足生产要求，整个机体在运行过程中表现为左右偏摆的不平衡运动，可利用阈值判断的方法进行诊断，但在早期磨损和移位时，虽有振幅差但满足生产要求，且对称测点的振动信号受到直线振动筛自身的振动和背景噪声的影响，信号中微弱的故障特征被淹没，从而导致早期不平衡故障难以诊断。

Huang等[2]提出了一种自适应非线性、非平稳信号分解方法—经验模态分解（empirical mode decomposition，EMD），将信号分解为一系列具有明确物理意义的本征模态函数（intrinsic mode function，IMF），在故障诊断领域[3-4]得到了广泛的应用，而该方法存在模态混叠问题，有Wu等[5-6]提出了总体经验模态分解（ensemble empirical mode decomposition，EEMD）、自适应噪声的完备经验模态分解（complete ensemble EMD with adaptive noise，CEEMDAN）等改进方法缓解该问题，但还存在计算量大、缺乏数学理论支撑等缺点。对此，Dragomiretskiy等[7]提出了变分模式分解方法（variational mode decomposition，VMD），该方法通过求解频域变分优化问题估计各个信号分量，VMD具有完善的数学理论支撑，且对噪声有较好的鲁棒性。徐元博等[8-9]利用变分模态分解，结合频率加权能量算子在强噪声背景下有效提取出双轴双电机多功能振动筛的轴承故障频率特征，还结合K-L散度应用于振动筛的轴承故障诊断。

此外，针对信号非线性、非平稳特征分析，Eckmann等[10]提出的递归图（recurrence plot，RP）利用相空间重构思想，以达到表征信号系统动力学特征的目的。Webber等[11]进一步对递归图中的细节结构进行描述，从而建立了递归量化分析方法（recurrence quantification analysis，RQA），构建了信号非线性、非平稳性的量化指标。由于该方法摆脱了数据统计分布假设的限制，能够克服传统方法对过程平稳的严格要求，具有广泛的适用性，近年来已先后在大气动力学、生物医学工程、机械故障诊断等领域[12-14]得到应用。

受上述研究启发，考虑直线振动筛原始振动信号的非线性、非平稳性和早期激振力不平衡故障特征的微弱性，将VMD和RQA相结合运用于直线振动筛早期运动不平衡故障故障诊断。对原始振动信号通过VMD分解，得到包含不同频带范围的信号分量，利用递归量化分析提取不同尺度的信号分量的非线性、非平稳特征，构建故障信号的非线性、非平稳性评价特征向量，并结合机器学习分类器，实现故障诊断。试验表明，在满足生产要求下，本文所提出的方法能有效区分偏心块移位引起的各类直线振动筛早期激振力不平衡故障，同时将该方法用于美国凯斯西储大学电气工程实验室的滚动轴承数据，说明了本方法具有一定的通用性和工程应用价值。

1 基本原理简介

1.1 变分模态分解

变分模态分解本质上是一个自适应最优Wiener波器组，它通过求解频域变分优化问题估计各个信号分量，该方法充分考虑了分量的窄带性质，自适应地确定相关频带。它假定原始信号f（t）被分解为K个变分模态分量，每个分量都是集中在各自中心频率附近的窄带信号，根据分量窄带条件建立约束模型

式中:{uk}，{ωk}分别为各变分模态分量和中心频率；δ（t）为狄拉克函数；*为卷积符号。为了求解最优约束模型，引入二次惩罚项α和Lagrange乘子λ，从而自适应地估计信号分量的中心频率以及重构相应分量，该方法实现步骤如下:

步骤1初始化Lagrange乘子、迭代次数n=0。

步骤2迭代次数n=n+1执行优化过程。

步骤3根据式（2）和式（3）更新{uk}和{ωk}。

步骤4根据式（4）更新λ。

步骤5重复步骤1～步骤4，直到满足式（5）迭代停止条件，结束循环，得到各变分模式分量。

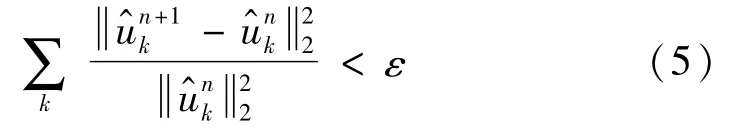
1.2 递归量化分析

递归图是递归量化分析的基础，递归图利用相空间重构思想，将一维时间序列，重构到高维相空间中，通过计算相空间中状态之间的距离计算揭示序列的局部相关信息，以达到表征信号系统动力学特征的目的。递归图的算法描述如下:

（1）对于采样时间间隔为Δt的时间序列uk（k=1，2，…，n），选择合适的嵌入维度m及延迟时间τ重构时间序列，重构后的动力系统为

式中，i=1，2，…，n-（m-1）τ。

（2）计算递归值

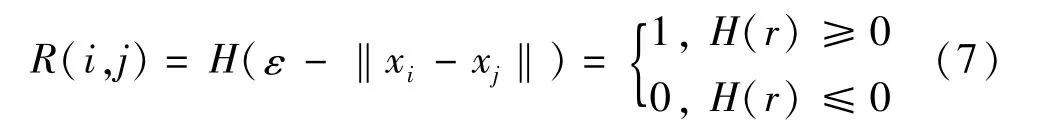
式中:‖xi-xj‖为欧几里得范数；ε为距离阈值；H（r）为Heaviside函数；R（i，j）为非0即1的递归值，以i为横坐标，j为纵坐标，得到一个N×N的状态距离矩阵，N=n-（m-1）τ，将0表示白点，1表示黑点，以二维图形表示，得到递归图。白点表明重构序列xi，xj之间不存在递归关系，黑点表明重构序列xi，xj之间存在递归关系。

对递归图上的各种动力学特征进行直观地分析需要一定的经验，若是一些典型的非线性、非平稳信号的递归图，能够定性确定其中一些特征所包含的意义。可实际信号往往是非典型的，因而需要通过递归量化分析，对递归图上所获得的各种特征进行定量处理。递归量化分析通过统计递归图中点以及线段等的分布特征，定量反映信号的动力学特征，分别有递归率（RR）、对角线平均长度（L）、对角线递归熵（DENTR）、确定率（DET）、捕获时间（TT）、竖直线递归熵（VENTR）、层状度（LAM）等几种量化指标，其参数的定义及计算公式如表1所示。

表1 递归量化指标的定义及计算公式Tab.1 The definition and calculation formula of recursive quantization metrics

2 信号采集及诊断方法设计

2.1 直线振动筛不平衡故障信号采集

以型号GLS10直线振动筛为研究对象，采用NI数据采集卡、PCB压电加速度传感器，工控机和上位机组成直线振动筛信号采集系统。根据工程经验，GLS10直线振动筛发生严重不平衡故障时表现为左右振幅不一致的横摆运动，尤其对比筛箱两侧弹簧底座上的振幅，其有效值差具有明显的不同，因此将传感器测点布置在弹簧底座上。试验平台如图1所示。

图1 试验平台左侧视角Fig.1 Left view of experimental platform

GLS10直线振动筛在额定工作条件下，激振马达工作频率为50 Hz，转速为960 r/min，筛箱固有振动频率为16 Hz，正常平衡状态下两侧振幅有效值在5～8 mm内，左右两侧振幅有效值相差不超过0.5 mm。如图2所示，通过调节左右两个激振器上的偏心块位置，实现直线振动筛的激振力不平衡运动。提取的激振力不平衡状态如表2所示，状态1为正常类型，状态2～状态9左右两侧振幅有效值相差不超过0.5 mm，符合实际生产要求，为早期不平衡运动故障类型。

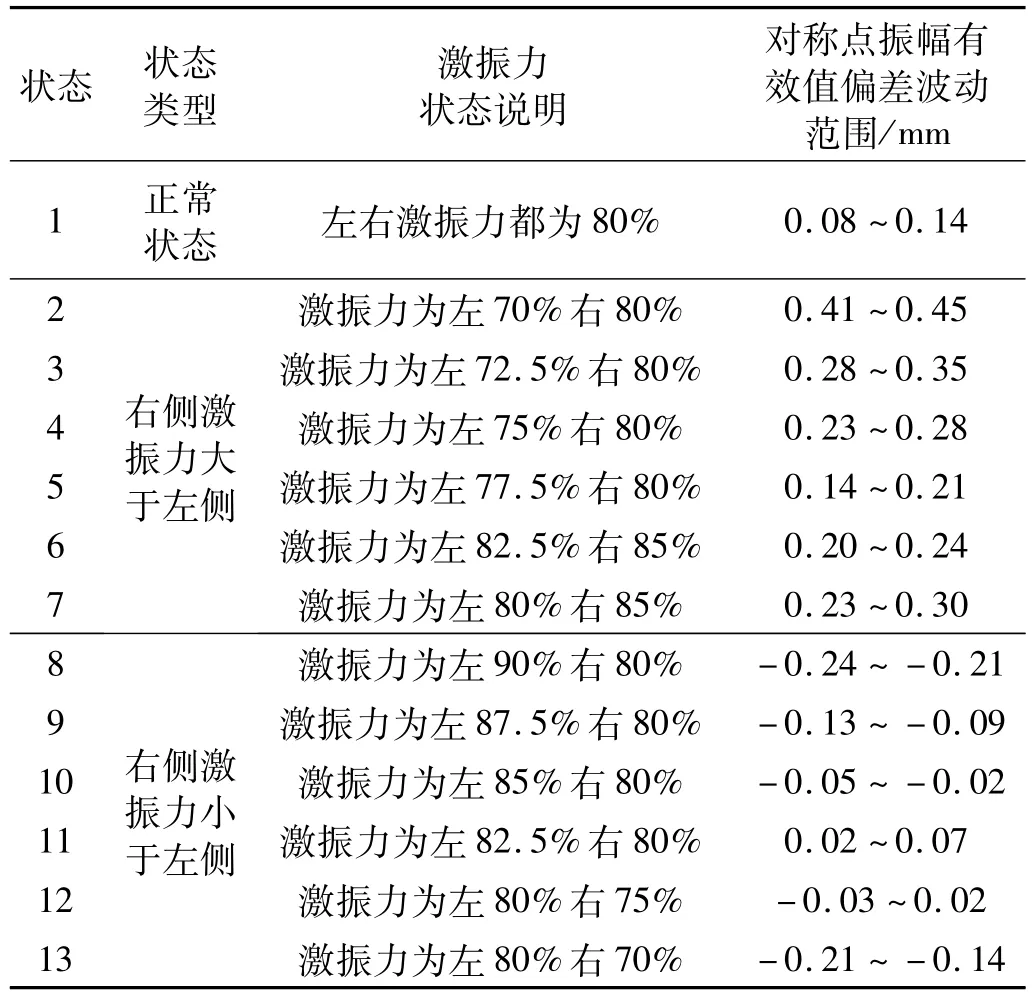
表2 直线振动筛激振力不平衡状态Tab.2 Unbalance state of excitation force of linear vibrating screen

图2 激振器及偏心块Fig.2 Vibration exciter and eccentric block

2.2 基于VMD-RQA的诊断方法设计

在本研究中，基于VMD-RQA的故障诊断流程图如图3所示，具体的应用试验步骤如下:

图3 基于VMD-RQA的故障诊断流程图Fig.3 Fault diagnosis flow chart based on VMD-RQA

步骤1在直线振动筛不同故障状态下，采集得到振动数据样本，选取一个弹簧底座上的传感器采集到的直线振动筛状态信号分别进行VMD分解，得到有限个IMF分量。

步骤2将每个IMF分量转化成递归图，并计算每个递归图中的递归量化参数指标，构成高维特征向量RQA。

步骤3将得到的高维特征向量输入分类模型进行训练，得到诊断模型。

步骤4重复步骤1～步骤3，构建测试样本高维特征向量，输入训练好的诊断模型中，从而区分直线振动筛激振力不平衡故障状态。

3 关键参数选取

3.1 VMD的参数确定

在VMD算法中，模态个数K和惩罚参数α对信号分解结果具有很大的影响。研究发现[15]分解个数较少时，原始信号中一些重要信息将会被滤掉丢失，信号的分解个数较多时，相邻模态之间会产生频率混叠；惩罚参数α越小，得到的各IMF分量带宽越大，反之，α越大各分量带宽越小。通过计算每个模态的中心频率和模态间的相关系数选择合适的模态个数，引入信噪比用来分析惩罚参数对VMD算法分解结果的影响。

选用对称点振幅有效值偏差波动范围最大的工况2进行VMD分解，不同K值下的中心频率分布如表3所示，各模态间的相关系数如表4所示。从表中可以看出，在模态分量个数大于5时，IMF3和IMF4的中心频率分别是958.99 Hz，1 098.14 Hz相距较近，且从表4可以看出IMF3和IMF4的相关系数R23相对较大，有局部的相关性，说明IMF3和IMF4出现模态混叠，因此模态个数选为4较适宜。

表3 不同K值下的中心频率Tab.3 Center frequencies at different values of K

表4 不同K值下的模态之间的相关系数Tab.4 Correlation coefficients between modes at different K

选择不同的惩罚参数做VMD分解，计算得到的信噪比值，如图4所示，从图中可知，随着惩罚参数α的不断增大，信噪比随之降低，并趋于平稳。信噪比指原始信号能量与噪声能量的比值，因此从滤波和消除噪声角度，信噪比不能过大，但重构后的信号需要能真实的还原原始信号，则需要选取较大的信噪比。因此选择惩罚参数α=2 000，以保证VMD分解过程中的去噪能力和细节保留度。对工况2的分解结果如图5所示，IMF1为频率为16 Hz的直线振动筛振动基频，IMF2中包含基频的倍频，IMF3和IMF4中包含着更高的故障或噪声频率。

图4 不同惩罚参数下的信噪比Fig.4 The SNR with different penalty parameter

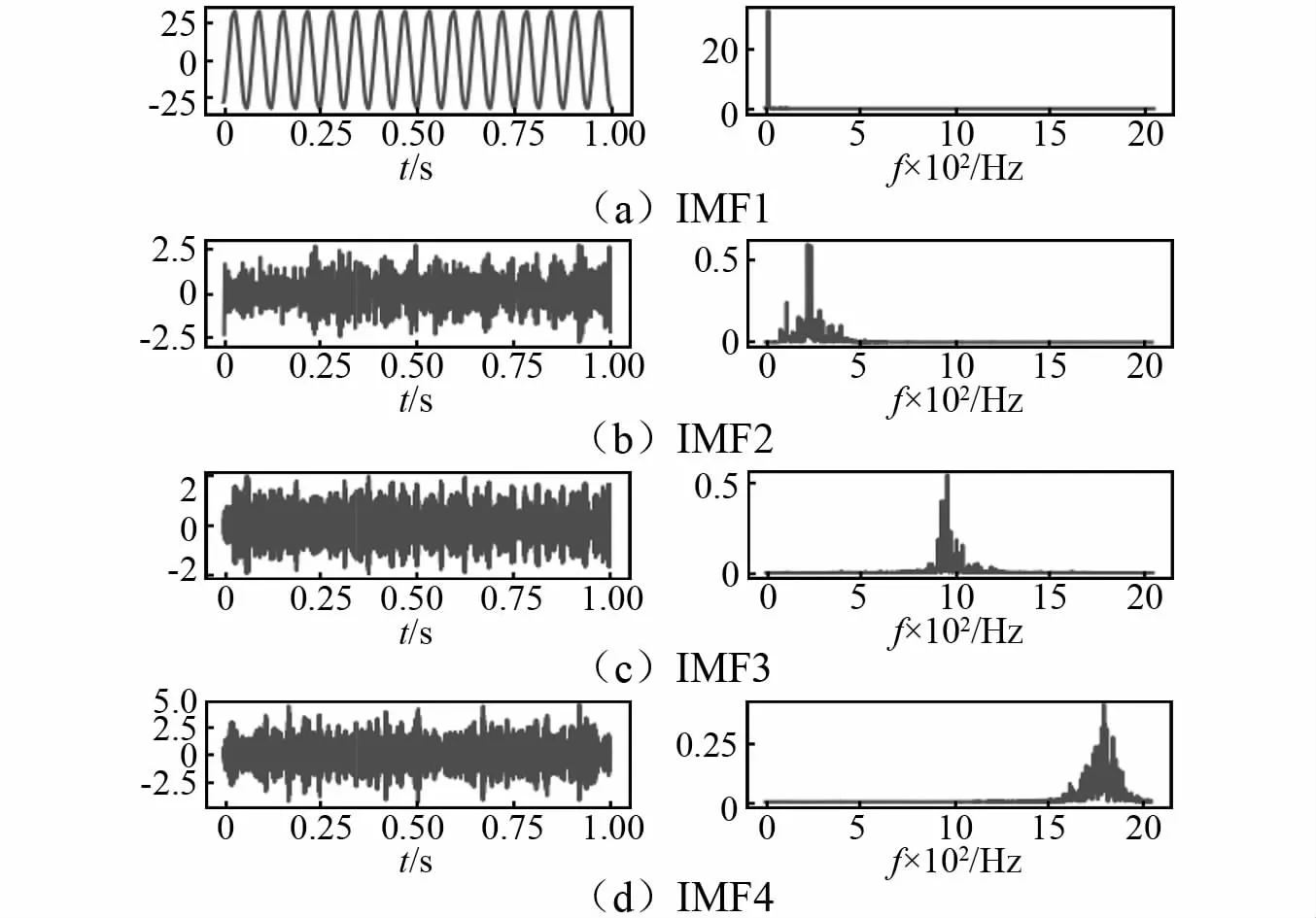
图5 状态2的VMD分解效果Fig.5 VMD decomposition effect of state 2

3.2 递归图和递归分析参数确定

相空间重构是递归图中不可缺少的一部分，因此选取合理的嵌入维度m和延迟时间τ非常关键。Sauer等[16-17]的结果证明了嵌入和延时的存在，但是他们没有告诉我们如何确定τ和m。迄今为止，尚无严格的数学结果提供确定这两个参数的独特途径。在没有这样的证据的情况下，已经提出了许多使用各种启发式考虑的方法来指导信号分析人员如何最佳选择τ和m。

采用Fraser等[18]提出的交互信息法，通过计算交互信息值，观察曲线第一次下降到极小值所对应的τ，确认是最佳延时时间。采用Cao[19]提出的改进的虚假最临近点法，只需要延迟时间τ一个参数，通过计算嵌入维数m～m+1的重构向量之间的平均最大范数之比E1（m）或平均欧氏距离之比E2（m），随着嵌入维数的增加，观察E1（m）和E2（m）曲线接近于1时所对应的m，确认是最佳嵌入维数。经过计算GLS10直线振动筛在以上13种工况下的相空间参数相差甚微，分别稳定在m=10，τ=3状态，限于篇幅，给出正常工况下的参数选取图，如图6所示。

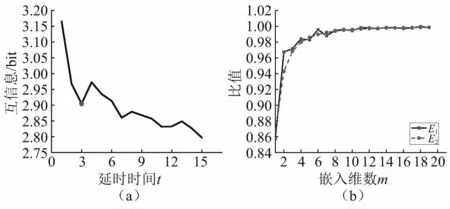
图6 相空间重构参数选择Fig.6 The selection of parameters for phase space reconstruction

距离阈值ε的选择也影响递归图的进一步分析，有一些研究[20]提出了确定最佳ε的方法。可选择‖xi-xj‖范数的最大距离、平均距离、标准差距离的某个百分比，或者全局固定阈值，或者固定递归率。ε的选择与我们希望研究的信号有内在的联系，随着ε的增加，增加了对具有递归关系的局部相关信息的容忍，即在递归图中出现更多的1，这将填充递归图中更细、更短的时间刻度结构。Goswami[21]指出若研究的重点是研究更长的时间尺度的行为，将递归率提高到30%以上是合适的。而本研究的数据采集时间跨度较长，采样点数较多，因此通过大量测试，将距离阈值ε设置为每个信号分量递归范数标准差距离的3倍。以正常状态信号为例，选择不同比例的标准差距离阈值，经VMD分解后，计算得到的各阶信号分量的递归率随着距离阈值变化关系，如图7所示，从图中可以看出当为3倍的标准差距离阈值时，各阶信号分量的递归率都达到30%以上，此时各阶模态分量转化的递归图，如图8所示。

图7 不同距离阈值下的递归率Fig.7 Recurrence rates at different distance thresholds

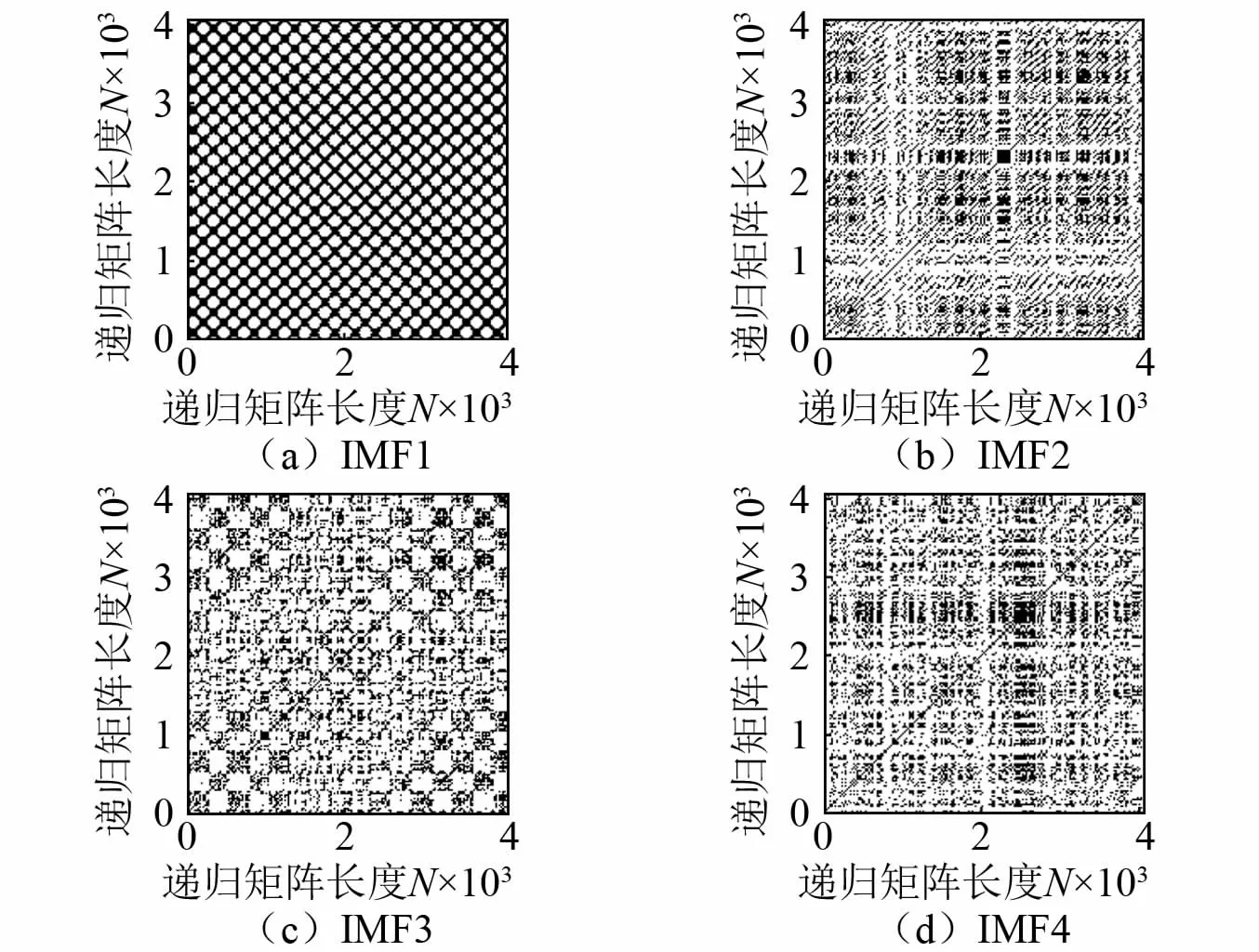
图8 正常工况下各模态的递归图Fig.8 Recurrence plot of various modes under normal conditions

4 试验分析

4.1 早期激振力不平衡故障诊断

对直线振动筛正常运行和早期不平衡故障等13种状态的振动信号，每种状态取500组，共6 500组数据，数据采样频率为4 096 Hz。从样本数据中随机抽取80%的数据，即5 200组数据作为训练样本，将剩下的20%数据作为测试样本。

对训练样本数据进行VMD分解，每个训练样本得到4个模态分量，分别转换为递归图；计算每个递归图的递归率、确定度、黑色对角线递归熵、捕获时间、层状度等7个递归量化指标，每个训练样本共得到4×7个指标，组成特征向量；输入到支持向量机、故障树、随机森林3种机器学习模型中进行训练，以十次交叉验证的结果作为最终的训练精度，从而消除随机因素的影响，建立分类模型。为了体现本方法的优越性，与传统的基于时域特征、基于频域特征的2种识别方法进行对比。故障识别结果对比如图9所示，可以看出，不管采用那种机器学习模型，基于传统时域特征的识别效果一般，而基频域特征和基于VMD-RQA特征的识别都有明显的提升，但识别率最高的是基于VMD-RQA特征的识别方法，相比于其他及其学习分类器，随机森林的诊断效果最佳，综合识别率达到了99.13%，能有效区分偏心块移位引起的各类直线振动筛早期激振力不平衡故障。

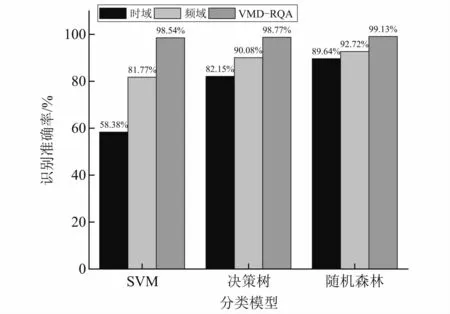
图9 直线振动筛故障识别结果对比Fig.9 Comparison of fault identification results of linear vibrating screen

探究VMD-RQA特征原理，RQA通过提取各模态信号内布局部信息之间的递归关系、分析各模态信号的非线性和非平稳性变化特征。如表5所示为随机森林诊断模型中的VMD-RQA各特征权重分布，可以看出基频IMF1和故障频段IMF3的RQA特征贡献率占了较大的体积质量，说明这两个频率段的RQA量化指标对激振力不平衡故障较为敏感，在发生故障时，IMF1和IMF3分量的非线性和非平稳性，有一定程度上的变化。此外，从表中还可以看出IMF1的递归率RR权重较为突出，对表2中13种工作状态的递归率特征进行对比，如图10所示，虽然各状态之间的递归率差甚微，但各自在一定范围内浮动，且正常状态与故障状态能有效区分，凸显了各工作状态之间的差异性，从图中还可以得出只有故障状态13和故障状态2、故障状态4和故障状态12的递归率特征有个别样本出现了混叠。

表5 随机森林训练特征权重分布Tab.5 Random forest training feature weight distribution

4.2 轴承故障诊断

旋转机械和振动机械在工作方式上，有所不同，因此为了更进一步说明该方法具有一定的通用性和实用价值，利用美国凯斯西储大学轴承数据中心的故障数据对所提方法进行实例验证。采用驱动端SKF6205深沟球轴承轴承数据，轴承转速为1 730 r/min，采样频率为48 kHz。轴承故障处由人工电火花加工制作，尺寸为0.18 mm，故障类型有滚动体故障、内圈故障和外圈故障。

首先，根据第三章所描述方法确定轴承信号进行分析的关键参数，得到模态分解个数K=4，惩罚参数α=2 000，嵌入维度m=6，延时时间τ=4，距离阈值ε为每个信号分量递归范数标准差距离的2.5倍。对正常、内圈故障、外圈故障、滚动体故障4种状态轴承的振动信号，每种状态取200组数据，共800组数据，从轴承样本数据中随机抽取80%的数据作为训练样本，将剩下的20%数据作为测试样本，同样与传统的基于时域特征、基于频域特征的2种识别方法进行对比，这里只使用随机森林训练，识别结果如表6所示。可以看出相比于传统方法，基于VMD-RQA的特征提取方法，综合识别率最高，为99.38%，仅有一个样本没有被准确识别。

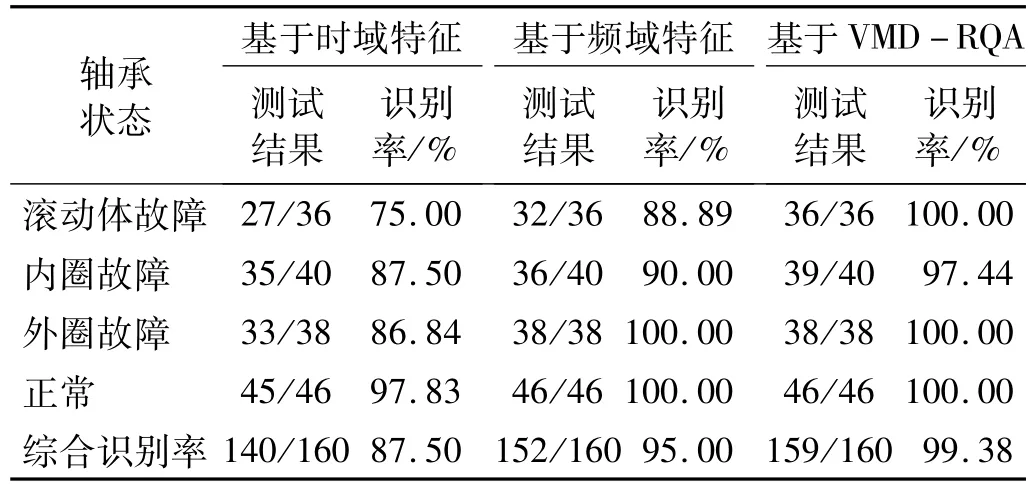
表6 轴承故障识别结果对比Tab.6 Comparison diagram of bearing fault identification results

5 结 论

针对直线振动筛早期激振力不平衡故障难以诊断问题。提出了一种基于VMD-RQA的故障诊断方法。通过现场试验和实例验证，得到以下结论:

（1）将VMD方法应用到直线振动筛早期激振力不平衡故障信号分析中，能有效分解得到直线振动筛自身的基频分量、故障及高频噪声分量。RP和RQA分析摆脱了数据统计分布假设的限制，揭示了信号内部的局部相关信息，及信号的非线性和非平稳的变化程度。

（2）对于偏心块移位引起的各类直线振动筛早期激振力不平衡的诊断，相比于传统诊断方法，基于VMD-RQA的诊断方法，得到了最高的识别精度，综合识别率为99.13%，能有效区分各类故障。

（3）振动机械与旋转机械运行原理不同，因此将该方法用于旋转机械轴承实例，综合识别率为99.38%，说明了本方法具有一定的通用性和工程应用价值。而振动机械中轴承故障作为引起激振力不平衡的另一个重要因素，这将是今后需要进一步研究的方向。