逆滞流迷宫密封气流激振特性研究

王佳蓉， 张万福，2， 姜广政， 杨兴辰， 李 春，2

（1.上海理工大学 能源与动力工程学院，上海 200093；2.上海理工大学 上海市动力工程多相流动与传热重点实验室，上海 200093；3.西安热工研究院有限公司，西安 710054）

非接触式迷宫密封具有结构简单、寿命长、摩擦损耗小等优势，被广泛应用于汽轮机、燃气轮机、航空发动机及压缩机等叶轮机械中，以减小流体由高压向低压部分泄漏[1]。然而，其周向贯通的结构特点易引发流体激振问题，对机组安全与稳定运行形成严峻挑战[2]。特别是随机组参数与容量不断提高，密封引起的失稳问题将愈加突出。因此，提高密封抗气流激振特性亟待解决。

近年，国内外学者对密封引起的失稳问题及流体激振机理展开了大量研究。当压力高点相对滞后于最小密封间隙，腔内气流会形成一个垂直转子位移方向的力，促进转子涡动[3]。引起密封流体激振的因素主要有:①Lomakin效应；②Alford效应[4]；③ 螺旋形流动效应[5]；④ 二次流效应[6]等。理论与试验研究发现，抑制流体周向流动是提高密封系统稳定性的有效手段之一。为此，学者们提出两种方法:① 阻旋栅阻旋；②射流阻旋。

阻旋栅是Benckert等[6]于1980年首次提出。通过在密封进口设置一系列径向分布的栅板来降低进口预旋速度，改善周向流动，提高稳定性。Childs等[7]对比了传统阻旋栅与逆阻旋栅迷宫密封的动力特性，表明逆阻旋栅能更好地抑制转子系统不稳定振动，减小流动损失。Sun等[8]结合数值模拟与试验方法研究阻旋栅密度、长度、压比、转速等对迷宫密封气流激振特性的影响，指出阻旋栅可有效抑制密封不稳定振动。Baldassarre等[9]及Alexandrina等[10]引入阻旋栅有效长度研究迷宫密封动力特性及泄漏特性，得出周向栅距与长度比存在最佳值。

射流阻旋迷宫密封开始被应用到离心压缩机[11]。Soto等[12]通过离心压缩机试验验证进口射流的有效性，指出逆向射流可以获得更大有效阻尼。压比小于0.45时，逆向射流迷宫密封稳定性甚至大于蜂窝密封。Kim等[13]沿迷宫密封周向布置12个逆向射流孔显著降低了交叉刚度，使密封结构涡动频率比提升至阻尼密封的2倍。Kim等[14]结合试验与计算流体力学方法分析迷宫密封轴向射流位置对密封动力特性系数的影响。表明射流位置越靠近高压端，交叉刚度与直接阻尼越小，但有效阻尼变化不显著。

上述两种方法通过抑制周向流动提高系统稳定性，取得良好的效果。但均存在空间利用率低、系统复杂性高等缺点，很大程度限制其推广使用。Zhang等[15]提出一种新型贯通式与间隔式逆滞流迷宫密封，通过在密封齿上布置射流孔，利用射流对密封腔内流动形成被动控制。但逆滞流喷嘴结构参数与位置对密封流体激振的影响还缺乏研究数据。

本文针对逆滞流迷宫密封，在迷宫密封进口第一个齿布置逆滞流喷嘴，研究其抗气流激振机理及影响因素。应用计算流体力学与多频涡动密封动力特性系数识别方法分析腔室周向速度及压力分布规律，研究逆滞流喷嘴结构参数与位置对密封动力特性及泄漏特性的影响。

1 数值计算方法

1.1 密封结构几何模型

Zhang等指出在密封第一个齿布置逆滞流喷嘴效果最佳，其他齿效果较小，且加工难度较大。因此，本文在迷宫密封第一个（#1）齿上布置一系列逆转动方向的微型喷嘴，使部分泄漏流体在进口高压作用下形成高速射流。图1、图2为逆滞流迷宫密封几何结构示意图，表1给出了具体几何参数，共包含10个梯形齿（#1～#10）。

图1 逆滞流迷宫密封二维几何示意图Fig.1 Two-dimensional structure of the anti-stagnant labyrinth seal

图2 密封-转子系统结构示意图Fig.2 The structure diagram of the seal-rotor system

表1 逆滞流迷宫密封几何参数Tab.1 Geometric parameters of the anti-stagnant labyrinth seal

图3为逆滞流喷嘴流域示意图，Ain，Aout为喷嘴进口与出口。在#1齿周向布置20个逆滞流喷嘴，单喷嘴周向扫略角度6°，逆转动方向偏转45°。

图3 逆滞流喷嘴流域示意图Fig.3 Schematic diagram of the anti-stagnant nozzle

1.2 数值模型

采用六面体结构化网格划分流动区域，对喷嘴、密封间隙等局部小尺寸、复杂流域进行单独加密处理。喷嘴扫略路径网格层数为12，端壁第一层网格高度为0.005 mm，Y+值在30～300。表2为网格无关性验证结果，其中Fij指i激励方向时j方向受力。240万网格与400万网格泄漏量相差0.35%。因此，综合考虑计算精度与计算资源，本文采用240万网格，图4为逆滞流迷宫密封网格分布情况。

表2 网格无关性验证Tab.2 Grid independence verification

图4 密封网格示意图Fig.4 Grid distribution of the seal

1.3 边界条件

应用ANSYS-CFX对密封流场进行求解，表3为主要工况参数。工质为空气（理想气体），湍流模型采用标准k-ε模型（5%湍流强度），壁面绝热光滑，近壁面采用壁面函数处理。给定进口总压Pin=500 kPa、总温Tin=298 K及出口静压Pout=100 kPa。以高精度离散格式完成迭代计算，收敛条件为能量、动量、连续性方程残差值均低于10-6，进出口流量差低于0.1%。瞬态计算气流力呈现周期性且相邻计算周期对应受力值相差低于0.001 N。

表3 计算工况Tab.3 Calculation conditions

1.4 动力特性系数识别方法

本文采用多频涡动方法来识别密封动力特性系数[16]，图5为单频下X方向激励（长轴位于X轴）与Y方向激励（长轴位于Y轴）转子涡动轨迹示意图。多频情况下，X，Y激励方向位移:

图5 转子涡动轨迹示意图Fig.5 Schematic diagram of the rotor whirling orbit

X激励方向

Y激励方向

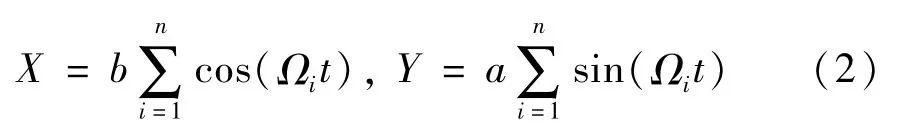
式中:X，Y分别为转子X，Y方向位移；a，b分别为椭圆轨迹长短轴；Ωi为涡动速度。

当转子进行小位移涡动时，忽略质量惯性力，气流激振力（FX，FY）可表示为

将位移、涡动速度等时域信号通过快速傅里叶变换转换为频域信号，X，Y激励方向式（3）化为:X激励方向

Y激励方向

定义阻抗系数Hij=Kij+j（ΩCij），Hii，Hjj为直接阻抗系数，Hij，Hji为交叉阻抗系数。将阻抗系数Hij代入式得

应用计算流体动力学（computational fluid dynamics，CFD）方法得到Fij，Dij，进而通过求解式（6）可得密封动力特性系数

2 计算结果与分析

有效阻尼Ceff是衡量密封系统稳定性的重要[17]

式中:C为平均直接阻尼，C=（CXX+CYY）/2；k为平均交叉刚度，k=（KXY-KYX）/2；Ω为涡动频率。

2.1 有效性验证

本文基于计算流体力学与多频涡动密封动力特性系数识别方法研究逆滞流迷宫密封气流激振特性。为验证其有效性，图6给出了传统迷宫密封有效阻尼系数的CFD计算与试验结果对比。可以看出，CFD计算结果与试验结果在数值和变化趋势上均具有较好的吻合性。

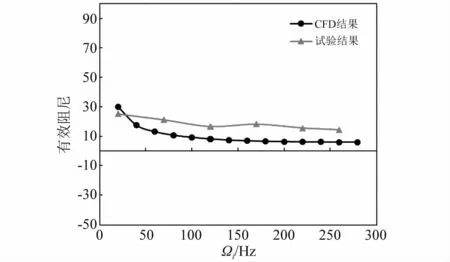
图6 CFD计算与试验结果对比Fig.6 Comparison of CFD calculation and experimental results

2.2 喷嘴进口高度对气流激振特性的影响

喷嘴进口高度不同直接影响进入#1腔射流强度，导致其对周向流动抑制效果改变。为此，计算了hin=1.00 mm，hin=0.34 mm，hin=0.25 mm，hin=0.17 mm下密封动力特性系数、周向速度及压力分布。

2.2.1 动力特性系数

图7～图9分别为不同喷嘴进口高度hin（hc=1.65 mm，hout/hin=0.5）下密封直接阻尼C、交叉刚度k、有效阻尼Ceff随涡动频率的变化情况。可以看出:①不同进口高度hin逆滞流喷嘴均可增大直接阻尼C、减小交叉刚度k、增加有效阻尼Ceff；②随喷嘴进口高度hin增加，直接阻尼C增加，交叉刚度k减小，有效阻尼Ceff增加，均利于提高系统稳定性；③直接阻尼C在各频率下均为正，且在高频下表现出较低频率依赖性；交叉刚度k在各频率下均为负，频率依赖性较低；有效阻尼Ceff在各频率下均为正，低频下随涡动频率增加而减小，高频下趋于定值；在低频下（＜100 Hz），直接阻尼C增幅与交叉刚度k减幅均较大，因此逆滞流喷嘴在低频下效果更显著。

图7 不同喷嘴进口高度下直接阻尼C随涡动频率变化Fig.7 Direct damping vs.whirling frequency for different inlet heights of the nozzle

图8 不同喷嘴进口高度下交叉刚度k随涡动频率变化Fig.8 Cross-coupled stiffness vs.whirling frequency for different inlet heights of the nozzle

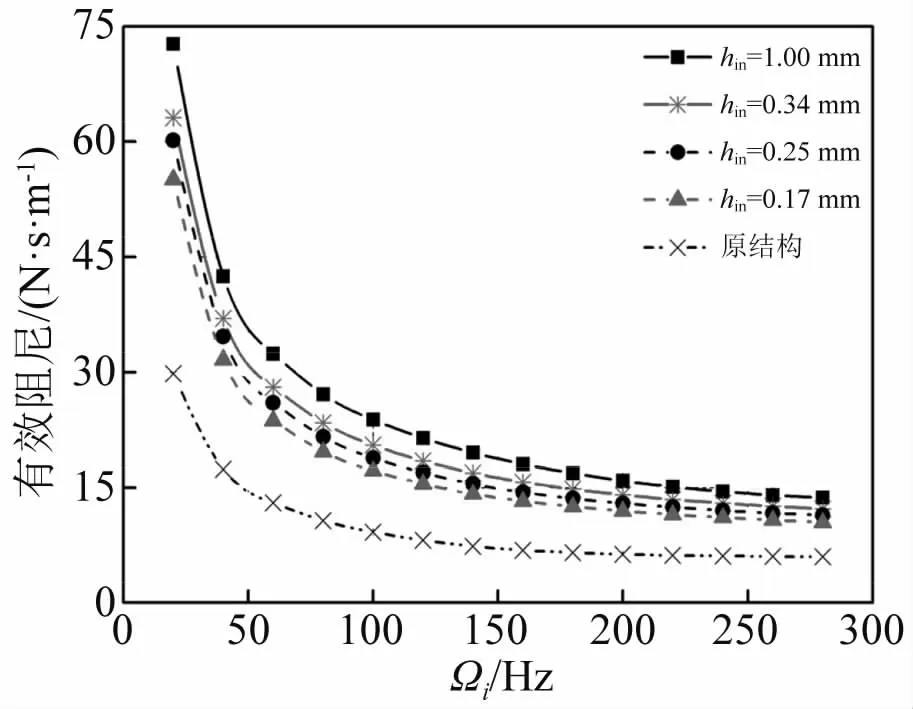
图9 不同喷嘴进口高度下有效阻尼C eff随涡动频率变化Fig.9 Effective damping vs.whirling frequency for different inlet heights of the nozzle

2.2.2 周向流动

图10为不同喷嘴进口高度hin下#1密封腔周向速度沿径向分布，D，U分别对应喷嘴下端与上端。逆滞流有效降低了密封腔周向速度，在远转子壁面处，周向速度反向。hin=1.00 mm，hin=0.34 mm，hin=0.25 mm，hin=0.17 mm对应的平均周向流速分别为-9.53 m/s，-10.21 m/s，-12.01 m/s，-12.72 m/s。 可见，随喷嘴进口高度增加，平均周向速度降低，绝对幅值增大，逆滞流作用效果越显著。在喷嘴附近，逆滞流对周向流动引导作用强，远离喷嘴后周向速度逐渐回升。进口高度较小时（hin=0.17 mm，hin=0.25 mm）喷嘴上下端之间存在明显极大值点，进口高度较大时（hin=0.353 mm，hin=1.000 mm）周向速度沿径向呈驼峰状。

图10 不同喷嘴进口高度下周向速度分布Fig.10 Circumferential velocity distribution for different inlet heights of the nozzle

图11为不同喷嘴进口高度下#1密封腔周向速度及喷嘴型心Ⅰ-Ⅰ处周向剖切面的速度分布，Ⅱ-Ⅱ对应喷嘴出口，z轴为旋转轴。逆滞流喷嘴使局部区域气流发生逆转，喷嘴附近出现一个低速区，周向速度最低达-30.480 m/s，显著抑制了#1腔周向流动。喷嘴进口高度对逆滞流量影响显著，hin=0.17 mm，hin=0.25 mm，hin=0.34 mm对应的逆滞喷嘴流量分别为9.051×10-5kg/s，1.346×10-4kg/s，1.718×10-4kg/s，而对流速影响较小，约107 m/s。随喷嘴进口高度增加，逆滞流量增加，喷嘴作用范围增大。

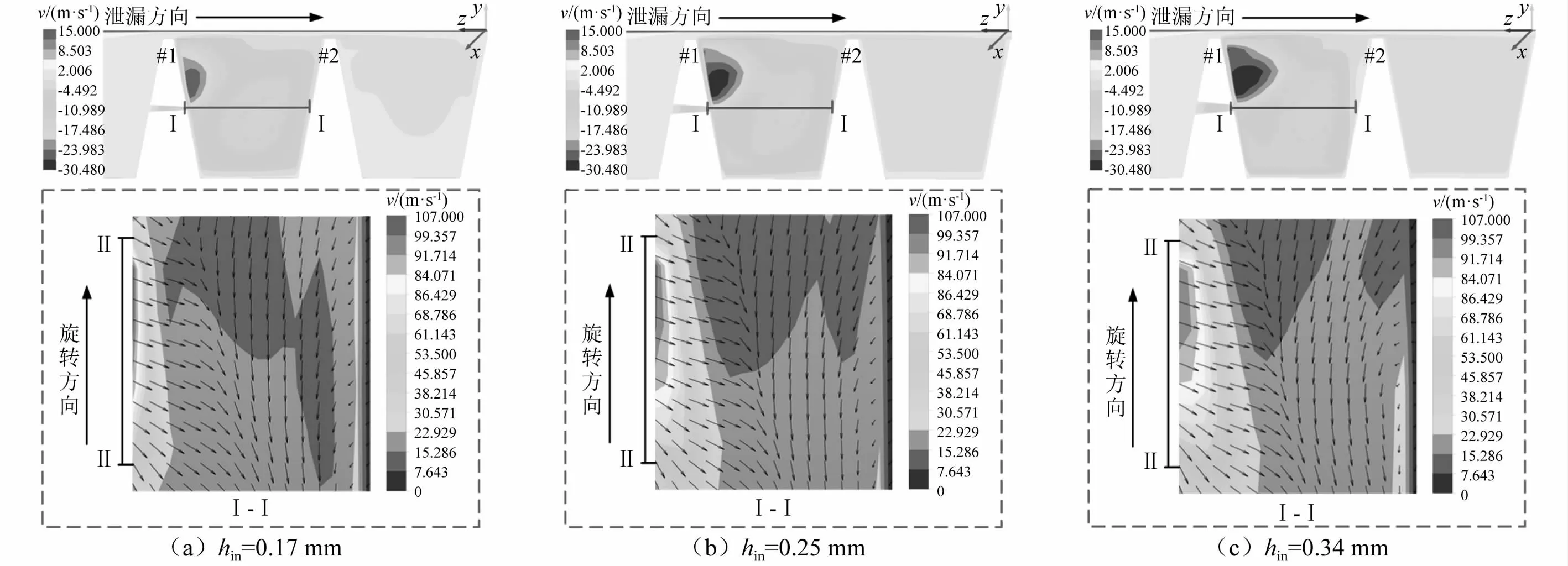
图11 不同喷嘴进出口高度下速度分布Fig.11 Velocity distribution for different inlet heights of the nozzle

图12为不同喷嘴进口高度下（y方向激励，t=0.1 s）#1密封腔平均周向压力。各进口高度下#1腔周向压力均呈正弦分布，且由于喷嘴作用，局部压力出现不同幅值波动。随密封进口高度增加，逆滞流量增加，#1腔压力绝对幅值增大。原密封结构压力高点约171°，设置逆滞流喷嘴后前移至144°～162°，有效减小了压力高点相对于最小密封间隙的偏移。

图12 不同喷嘴进口高度下周向压力分布Fig.12 Circumferential pressure distribution for different inlet heights of the nozzle

2.3 喷嘴进出口比例对气流激振特性的影响

上述结果表明:增加喷嘴进口高度可提高其抑制气流激振效果。下文进一步研究喷嘴进出口比例对气流激振特性的影响，计算分析hout/hin=0.25，hout/hin=0.50，hout/hin=0.75时密封动力特性系数及周向压力与速度分布。

2.3.1 动力特性系数

图13～图15分别为不同喷嘴进出口比例hout/hin（hin=1.00 mm，hc=165 mm）下密封直接阻尼C、交叉刚度k、有效阻尼Ceff随涡动频率的情况。可以看出:①不同进出口比例hout/hin逆滞流喷嘴均使直接阻尼C增加、交叉刚度k减小，有效阻尼Ceff增加；②在各频率下随喷嘴进出口比例hout/hin增加，交叉刚度k增加，有效阻尼Ceff减小，直接阻尼C变化不显著；③直接阻尼C在各进出口比例下均为正，低频下频率依赖性较高；交叉刚度k在各进出口比例下均为负，喷嘴增加了其频率依赖性，随涡动频率增加而增加；有效阻尼Ceff在各进出口比例下均为正，高频下频率依赖性较低；交叉刚度k对有效阻尼Ceff的贡献随涡动频率增加而减小，因此，低频下（＜150 Hz）hout/hin越小，有效阻尼Ceff越大，逆滞流作用越显著。

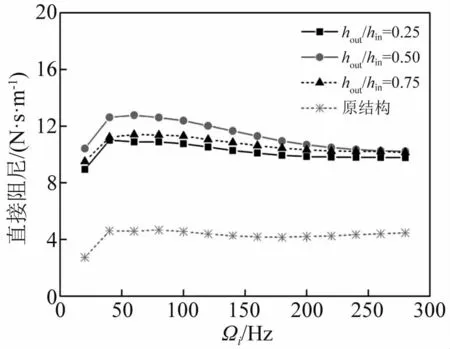
图13 不同进出口比例下直接阻尼C随涡动频率变化Fig.13 Direct damping vs.whirling frequency for different ratios of inlet/outlet height

图14 不同进出口比例下交叉刚度k随涡动频率变化Fig.14 Cross-coupled stiffness vs.whirling frequency for different ratios of inlet/outlet height

图15 不同进出口比例下有效阻尼C eff随涡动频率变化Fig.15 Effective damping vs.whirling frequency for different ratios of inlet/outlet height

2.3.2 周向流动

图16为不同喷嘴进口比例hout/hin下#1密封腔周向速度沿径向分布，D，U分别对应喷嘴下端与上端。逆滞流有效降低了#1腔周向速度，除转子、静子附近周向速度反向。hout/hin=0.25，hout/hin=0.50，hout/hin=0.75对应的平均周向速度分别为-15.08 m/s，-12.72 m/s，-9.24 m/s。可见，随喷嘴进出口比例hout/hin增加，平均周向速度增加，绝对幅值减小。各hout/hin周向速度沿径向呈驼峰状，喷嘴上下端之间存在明显极大值点。hout/hin=0.50周向速度在半径32.0～33.2 mm低于hout/hin=0.25，但hout/hin=0.25除转子附近均为负，对周向流动控制范围更广。

图16 不同进出口比例下周向速度分布Fig.16 Circumferential velocity distribution for different ratios of inlet/outlet height

图17为不同喷嘴进出口比例下#1密封腔周向速度及喷嘴型心Ⅰ-Ⅰ处周向剖切面的速度分布云图，Ⅱ-Ⅱ对应喷嘴出口，z轴为旋转轴。逆滞流能有效抑制#1腔周向流动，使腔内大部分区域气流周向速度反向，腔内出现两个低速区，最低周向速度达-25.613 m/s。进出口比例对逆滞流参数影响显著，hout/hin=0.25，hout/hin=0.50，hout/hin=0.75对应的逆滞流速分别为:47.867 9 m/s，54.894 6 m/s，68.700 6 m/s，流量分别为:2.850×10-4kg/s，4.264×10-4kg/s，5.100×10-4kg/s。

图17 不同进出口比例下速度分布Fig.17 Velocity distribution for different ratios of inlet/outlet height

可见，随进出口比例hout/hin增大，逆滞流量增加，流速减小。据3.1节逆滞流量越大对周向流动抑制效果越佳，但腔内周向流速减小，低速区敛缩。因此，喷嘴进出口比例变化时逆滞流速对腔内周向流动的控制占主导。

图18为不同进出口比例下（y方向激励，t=0.1 s）#1腔平均周向压力。各进出口比例下#1腔周向压力均呈正弦分布，逆滞流汇入使其局部出现不同幅值波动。随进出口比例hout/hin增加，逆滞流量增大、流速减小，增大了#1腔压力绝对幅值，削弱了喷嘴局部作用效果，压力波动弱化。原密封结构压力高点约171°，设置逆滞流喷嘴后前移至135°～153°，有效减小了压力高点相对于最小密封间隙的偏移。

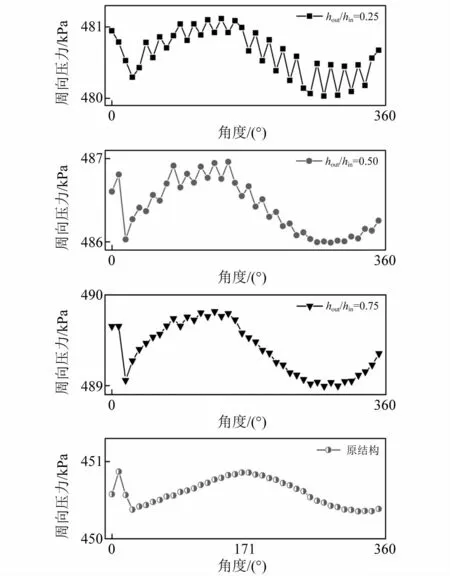
图18 不同进出口比例下周向压力分布Fig.18 Circumferential pressure distribution for different ratios of inlet/outlet height

2.4 喷嘴型心高度对气流激振特性的影响

上述结果表明:减小喷嘴进出口比例hout/hin可提高其抑制气流激振效果。下文将进一步研究喷嘴型心高度对气流激振特性的影响，计算分析hc=0.70 mm，hc=1.65 mm，hc=2.10 mm密封动力特性系数及周向压力与速度分布。

2.4.1 动力特性系数

图19～图21分别为不同喷嘴型心高度hc（hin=1.00 mm，hout/hin=0.25）下密封直接阻尼C、交叉刚度k、有效阻尼Ceff随涡动频率的变化情况。可以看出:①不同型心高度hc逆滞流喷嘴均使直接阻尼C增加，交叉刚度k减小，有效阻尼Ceff增加；②在各频率下喷嘴型心高度hc=1.65 mm（径向中心）时交叉刚度k最小，直接阻尼C相当，有效阻尼Ceff最大；③直接阻尼C在各型心高度下均为正，大于40 Hz频率依赖性较低；交叉刚度k在各型心高度下均为负，设置逆滞流喷嘴增加了其频率赖性，随涡动频率增加而增加；有效阻尼Ceff在各型心高度下均为正，大于150 Hz频率依赖性较低；低频下hc=1.65 mm直接刚度k减幅较大，因此对气流激振抑制效果更显著。

图19 不同型心高度下直接阻尼C随涡动频率变化Fig.19 Direct damping vs.whirling frequency for different centroid heights

图21 不同型心高度下有效阻尼C eff随涡动频率变化Fig.21 Effective damping vs.whirling frequency for different centroid height

2.4.2 周向流动

图22为不同喷嘴型心高度下#1密封腔周向速度沿径向分布。D1，U1，D2，U2，D3，U3分别对应hc=2.10 mm，hc=1.65 mm，hc=0.70 mm喷嘴上端与下端。逆滞流有效改善了#1腔周向流动，除壁面附近周向速度反向。hc=0.70 mm，hc=1.65 mm，hc=2.10 mm对应的平均周向速度分别为-13.11 m/s，-15.08 m/s，-17.55 m/s。可见，随喷嘴型心高度增加，平均周向速度降低，绝对幅值增大。hc=2.10 mm周向速度除转子附近均为负，对周向流动控制范围更广。

图22 不同型心高度下周向速度分布Fig.22 Circumferential velocity distribution for different centroid heights

图20 不同型心高度下交叉刚度k随涡动频率变化Fig.20 Cross-coupled stiffness vs.whirling frequency for different centroid heights

图23为不同喷嘴型心高度下#1密封腔周向速度分布及喷嘴型心Ⅰ-Ⅰ处周向剖切面速度分布云图，Ⅱ-Ⅱ对应流喷嘴出口，z轴为旋转轴。逆滞流喷嘴显著降低了#1腔周向速度，使腔内出现数目不等的低速区。逆滞流参数对型心高度不敏感，三种型心高度下逆滞流量约2.84×10-4kg/s，流速约68.32 m/s。hc=2.10 mm低速区效果最明显，腔内出现两个低速区，最低周向速度达-30.842 m/s。hc=1.65 mm对腔内周向流动控制范围更广，绝大部分区域为周向速度反向。

图23 不同喷嘴型心高度下速度分布Fig.23 Velocity distribution for different centroid heights

图24为喷嘴型心高度下（y方向激励，t=0.1 s）#1密封腔平均周向压力。各型心高度下#1腔周向压力均呈正弦分布，逆滞流汇入使其局部出现不同幅值波动。随喷嘴型心高度增加，#1腔压力绝对幅值下降。原密封结构压力高点约171°，设置逆滞流喷嘴后前移至144°～153°，有效减小了压力高点相对于最小密封间隙的偏移。

图24 不同喷嘴型心高度下周向压力分布Fig.24 Circumferential pressure distribution for different centroid heights

2.5 泄漏量

表4为逆滞流迷宫密封泄漏量对比，相比原结构，逆滞流迷宫密封泄漏量略有上升，增幅小于4%；随喷嘴进口高度hin增大、喷嘴进出口比例hout/hin增大、喷嘴型心高度hc增大，逆滞流迷宫密封泄漏量上升。

表4 逆滞流迷宫密封泄漏量Tab.4 Leakage flowrate of anti-stagnant labyrinth seals

3 结 论

本文针对逆滞流迷宫密封，采用计算流体力学与多频涡动密封动力特性系数识别方法研究喷嘴进口高度、进出口比例、型心高度等参数对密封动静特性的影响，结果表明:

（1）逆滞流喷嘴能有效抑制周向流动，改善腔内压力分布，提高密封抗气流激振特性。较之于传统迷宫密封，逆滞流迷宫密封直接阻尼增加、交叉刚度减小、有效阻尼增加，且低频下效果更显著；逆滞流作用下#1密封腔周向速度大幅降低。

（2）相同结构参数逆滞流喷嘴的径向位置存在最佳值，当型心高度hc=1.65 mm（径向中心）时密封有效阻尼最大；增加逆滞流喷嘴进口高度、减小进出口比例均有利于提高密封稳定性；进口高度hin=1.00 mm、进出口比例hout/hin=0.25、型心高度hc=1.65 mm为计算工况下的最佳结构。

（3）随喷嘴进口高度hin增大、喷嘴进出口比例hout/hin增大、喷嘴型心高度hc增大，逆滞流迷宫密封泄漏量上升。因此，逆滞喷嘴的位置与射流方向还有待进一步研究。