基于谐波小波变换的滑动轴承油膜涡动与振荡故障识别与分析
姚明镜,张春良,,岳夏,朱厚耀
(1.南华大学 机械工程学院,湖南 衡阳 421001;2.广州大学 机械与电气工程学院,广州 510006)
油膜涡动与振荡是导致滑动轴承高振动的常见油膜故障,掌握油膜涡动与振荡的特征,有助于对轴承故障做出准确及时的诊断[1]。长期以来,旋转机械的故障诊断主要采用振动信号频谱分析,通过滤波技术处理振动信号后进行故障分析判断[2]。FIR数字滤波器是数字信号处理系统中最基本的元件,信号通过它不失真的在通带内具有恒定的幅频响应和线形相位特性,其线性相位特性满足了现代信号处理领域对滤波器的高性能要求,成为应用最广泛的数字滤波器。
近年来,也有多种滤波技术应用于振动信号处理,如在信号的截断频带上具有较好信号分辨率的Vondrak滤波[3-4],在时域和频域具有良好局部化特性的小波滤波[5],利用观测向量预测和修正新状态向量的Kalman滤波[6]等。这些滤波在处理线性稳定信号方面都具有各自的优势,但对于油膜涡动与振荡这类非平稳非线性信号,以上滤波方法信号处理效果均不明显[4]。而谐波小波具有频域盒形紧支谱特性及良好的相位定位能力[7],在处理非平稳非线性信号时更有优势。故利用谐波小波滤波对油膜涡动与振荡进行处理分析,并将其与最基本且运用最成熟的FIR滤波进行对比分析,以验证其有效性和准确性[8]。
1 油膜涡动与振荡的原理及特征
1.1 油膜涡动与振荡的原理
油膜涡动与振荡是滑动轴承在高速运行时特有的一种故障[9],其工作原理图如图1所示。
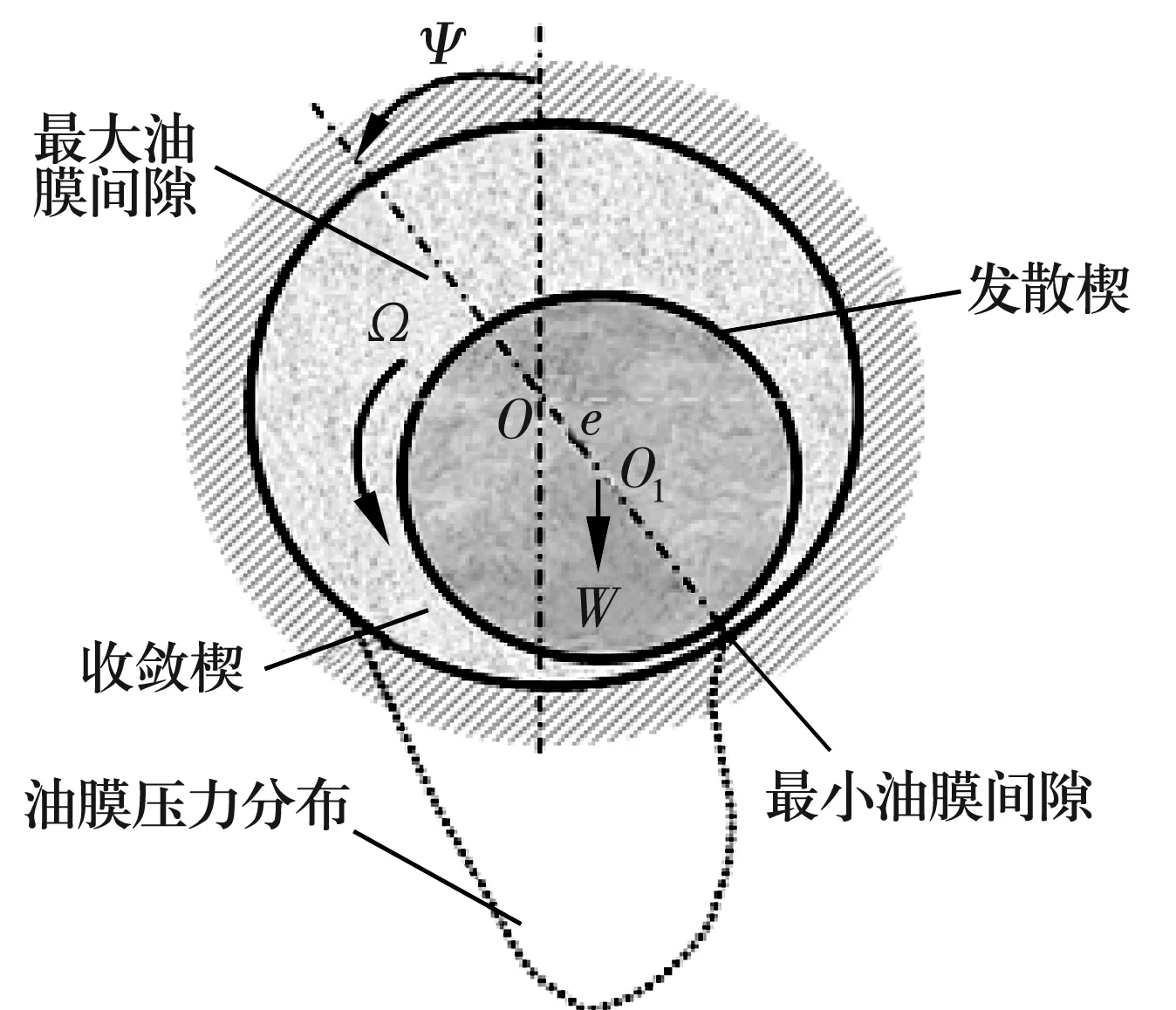
图1 油膜轴承工作原理
转子在正常工作状态时,轴颈与轴承中心不重合,而是存在偏心距e。油膜稳定、载荷固定不变时,偏心距不变,机组运行稳定,油膜压力P与轴颈上的载荷W处于平衡状态;当外界向轴颈施加扰动力,轴心O1位置会偏移Δe从而处于新位置,油膜压力变为P′,与此时的载荷W′不平衡。设轴颈上的载荷与油膜压力的合成力为F,其分力F1推动轴颈回到初始平衡位置O1,分力F2使轴颈既以角速度Ω自转,又绕O1涡动,涡动速度v为角速度Ω的1/2,称之为油膜涡动[10]。
工程中发生油膜涡动时,涡动频率一般为转子速度的0.43~0.48倍。若转子的转速升至一阶临界转速的2倍时,涡动频率等于一阶临界转速,发生机械共振,振幅陡然变大,振动剧烈,轴心轨迹杂乱,形成不规则曲线,基频振幅与半频谐波的振幅非常接近甚至相等。转速如果继续增大,涡动频率与转子一阶临界转速保持一致,而且不再变化,称之为油膜振荡[11]。
1.2 油膜涡动与振荡的特征
油膜涡动与振荡主要通过振动信号的时频信号进行识别分析,振动信号的时域波形、轴心轨迹等在油膜涡动与振荡故障发生时都会产生变化,这些变化反映了油膜涡动与振荡的故障特征[12]:(1)在低速阶段,频谱图上出现半速涡动成分,涡动频率与转速频率之比为0.3~0.5。当转速为2倍一阶临界转速时,发生油膜振荡;(2)出现油膜涡动时的轴心轨迹为“内8”形(即大环套小环),油膜振荡发生时轴心轨迹为混乱无规则的曲线;(3)滑动轴承的这2种特有故障均为正进动,即涡动与旋转的方向相同。
2 谐波小波变换
谐波小波是一种复小波,其伸缩平移构成了L2(R)空间的规范正交基[13]。通过信号的快速Fourier变换及其逆变换实现谐波小波的分解[14-15]。
2.1 谐波小波的定义及正交性
考虑到小波是满足允许条件的函数,一个小波若具有完全盒形的频谱将是非常理想的。故假设有实偶函数ωe(t)和实奇函数ωo(t),其Fourier变换分别为
(1)
(2)
对W(ω)=We(ω)+jWo(ω)有
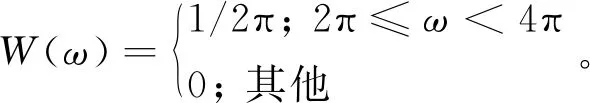
(3)
则ω(t)=ωe(t)+jωo(t)由W(ω)进行Fourier逆变换为
(4)
(4)式定义的函数即为谐波小波,是在频域紧支且具有完全盒形的频谱。以小波为理论基础对谐波小波伸缩、平移,生成谐波小波函数簇为
(5)
式中:i为小波变换尺度。在时间尺度上(5)式是(4)式的变形,即拉伸或压缩变形的结果,而位置则会沿时间轴运动k个新尺度单位1/2i [16-19]。
2.2 谐波小波滤波
谐波小波是一个非常理想的带通滤波器,可定义为
(6)
m,n决定了谐波小波变换的尺度i,且n=2m,当m=0时,n=1。可以用卷积运算表示小波变换的内积运算。对一定尺度的小波μ(t),信号x(t)的小波变换为
(7)
则x(t)相对于尺度i的谐波小波μm,n(t)的小波变换为
(8)
根据Fourier变换的性质,时域中的卷积等于频域中的乘积,则
(9)
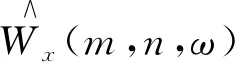
谐波小波的优点是具有明显的数学表达式以及光滑性、盒形谱特性、零相移特性等,在不同尺度下可构造各频段数据点数和采样频率固定不变的算法,最终用于分析转子轴心轨迹[20]。
3 基于虚拟仪器的试验分析
如图2所示,利用Bently模拟转子试验台进行试验[21-22],信号采集卡为NI9234:24位、采集电压±5 V,4路数字输入和输出,支持USB2.0,无需外部供电。带有信号前置适配器、油膜涡动所需的轴承油泵系统和转速控制调节装置。

图2 转子试验台
转轴中部的支架上安装有2个相互垂直的非接触式电涡流传感器,分别测量转子x,y方向的振动信号[23],采样频率为2 000 Hz。
3.1 油膜涡动与振荡的发生过程
调节转子转速,使其由1 000 r/min升至5 000 r/min,并对整个过程进行持续测量。观察转轴x,y方向的信号发现,整个过程中工频幅值先增后减,当转速在3 500 r/min左右时,幅值处于最大值,可知一阶临界转速在3 500 r/min左右浮动。转速在3 200 r/min左右时,开始出现油膜涡动,当转速为4 000和4 500 r/min时,涡动频率分别为32和38 Hz。在转速升高的过程中,油膜涡动频率随之升高,但一直低于一阶临界转速,此时并未发生油膜振荡。
分析转速从3 000 r/min升高到7 200 r/min的过程发现,当转速升至7 000 r/min时,涡动频率为58.4 Hz,达到了一阶临界转速,涡动频率所对应的幅值急剧增大,此时已发生油膜振荡。
3.2 故障信号处理与分析
分别对转子3 400和6 900 r/min时的油膜涡动与振荡信号进行分析。油膜涡动x,y方向的振动信号如图3所示。由图可知,未经滤波的信号有很多干扰信号,很难辨别想要获取的信号。经FIR数字滤波和谐波小波滤波的振动信号分别如图4、图5所示。
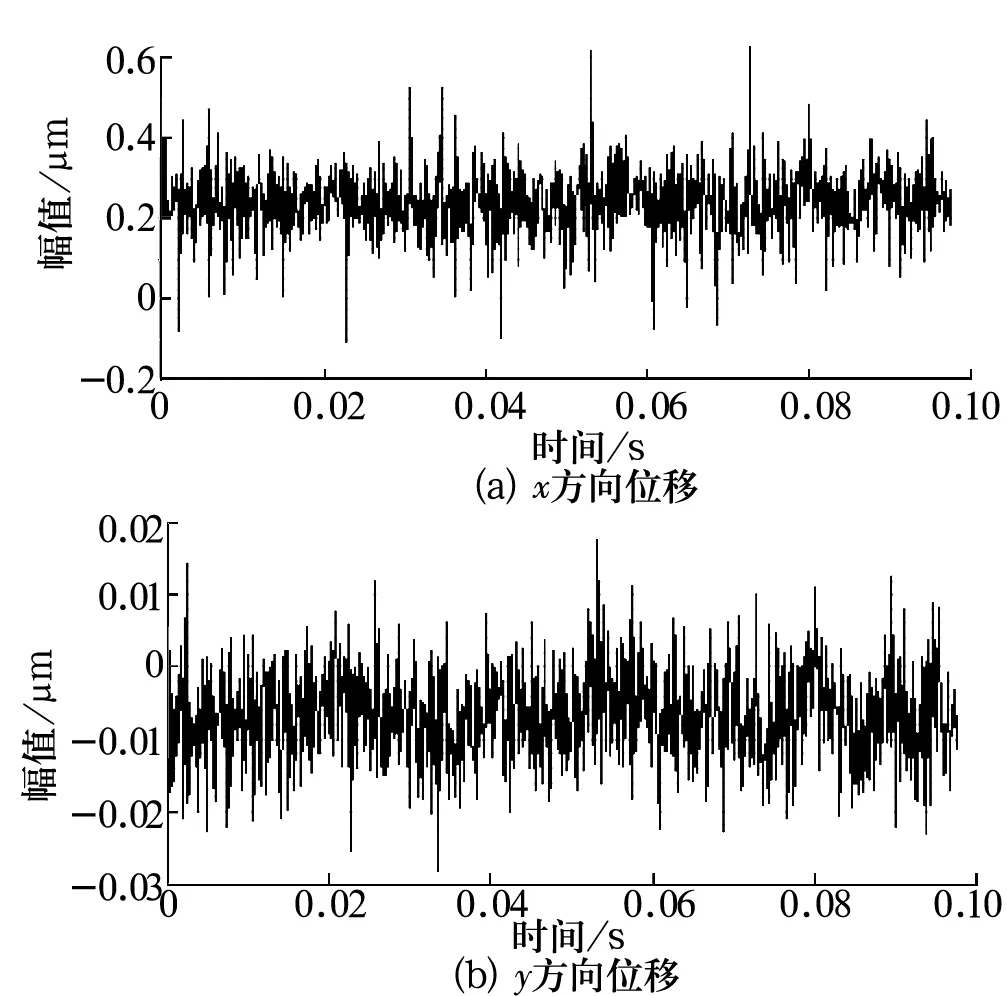
图3 油膜涡动x,y方向振动信号的时域波形
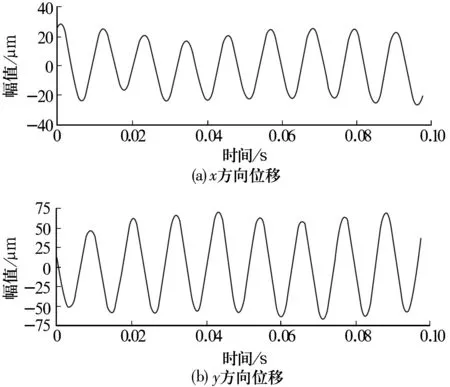
图4 FIR滤波后x,y方向振动信号的时域波形
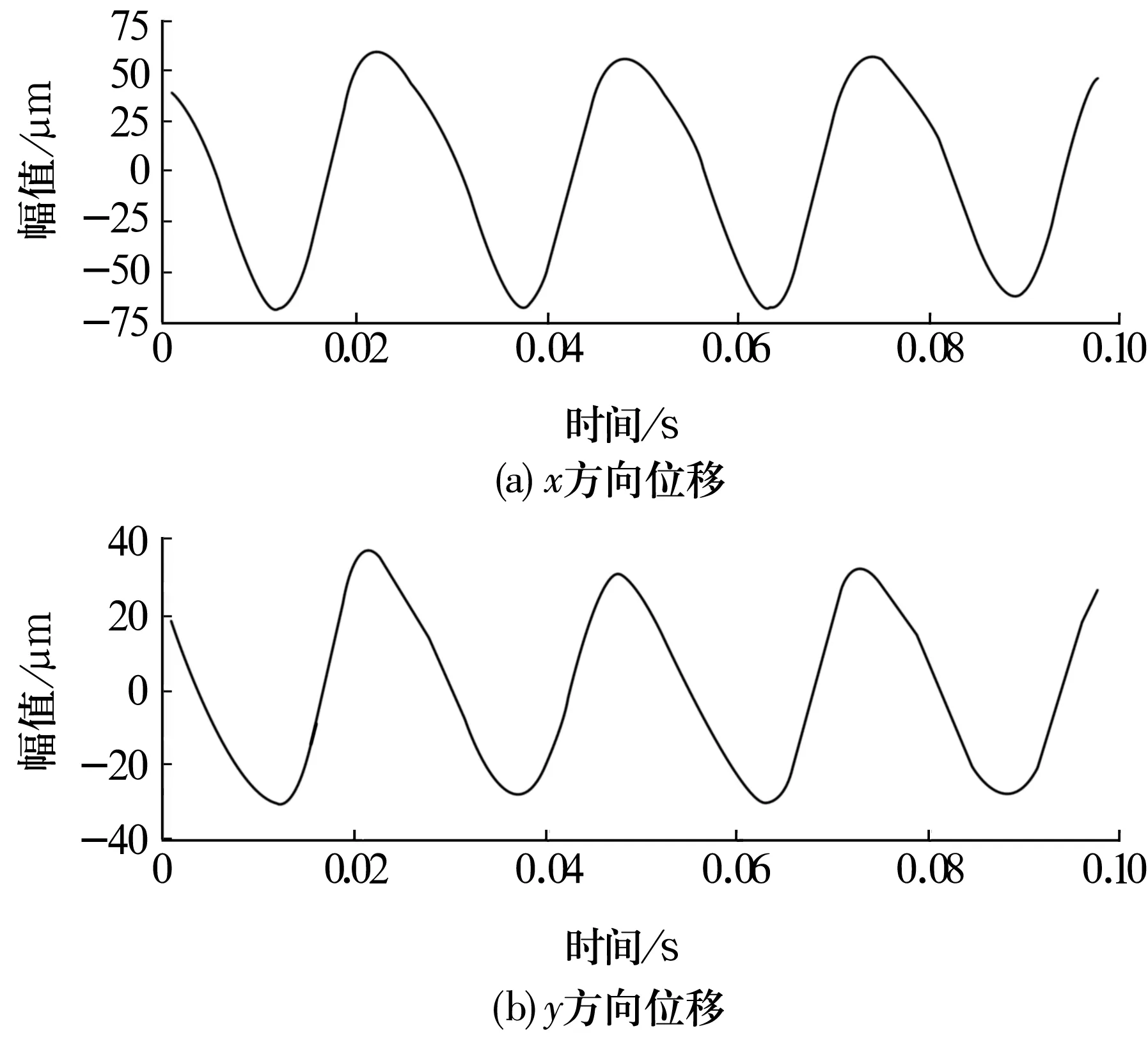
图5 谐波小波滤波后x,y方向振动信号的时域波形
由图可知,油膜涡动的振动信号经滤波后都得到了单一的规律性波形,表现为正弦波形。与设定提取的油膜涡动信号波形一致。但经谐波小波滤波的信号波形更加平稳,几乎是标准的正弦波形,而经FIR滤波的信号高低不平,与标准正弦信号有所不同。因此,对于油膜涡动与振荡这类非平稳轴承故障的信号,谐波小波滤波更具优越性。其过滤了不稳定的晃动信号,同时也提高了信号与背景的对比度,有利于提高后续检测和识别等过程的准确性。
为了识别油膜涡动与振荡发生时的频域特征,对其振动信号进行幅值谱分析,结果如图6、图7所示。
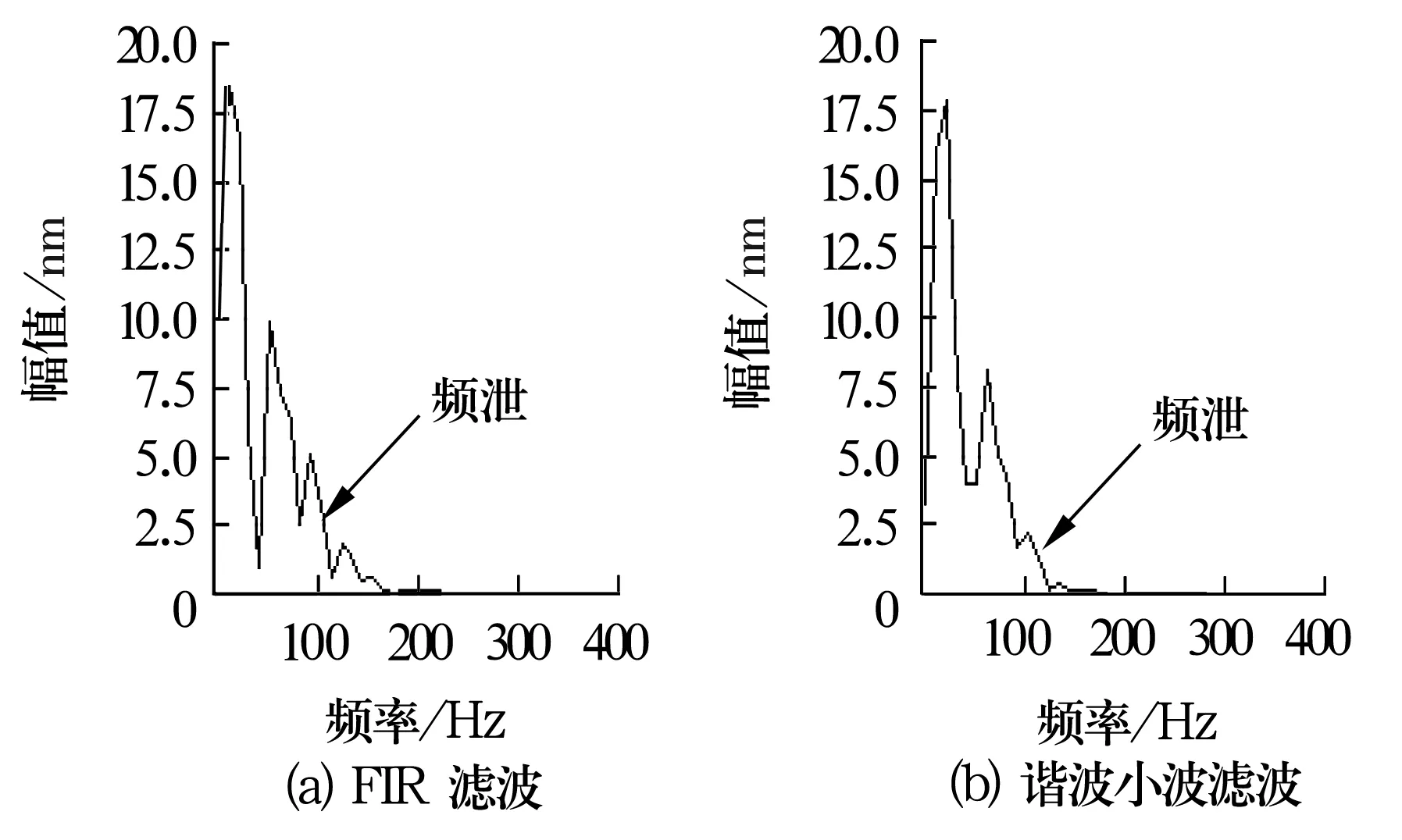
图6 油膜涡动滤波信号幅值谱
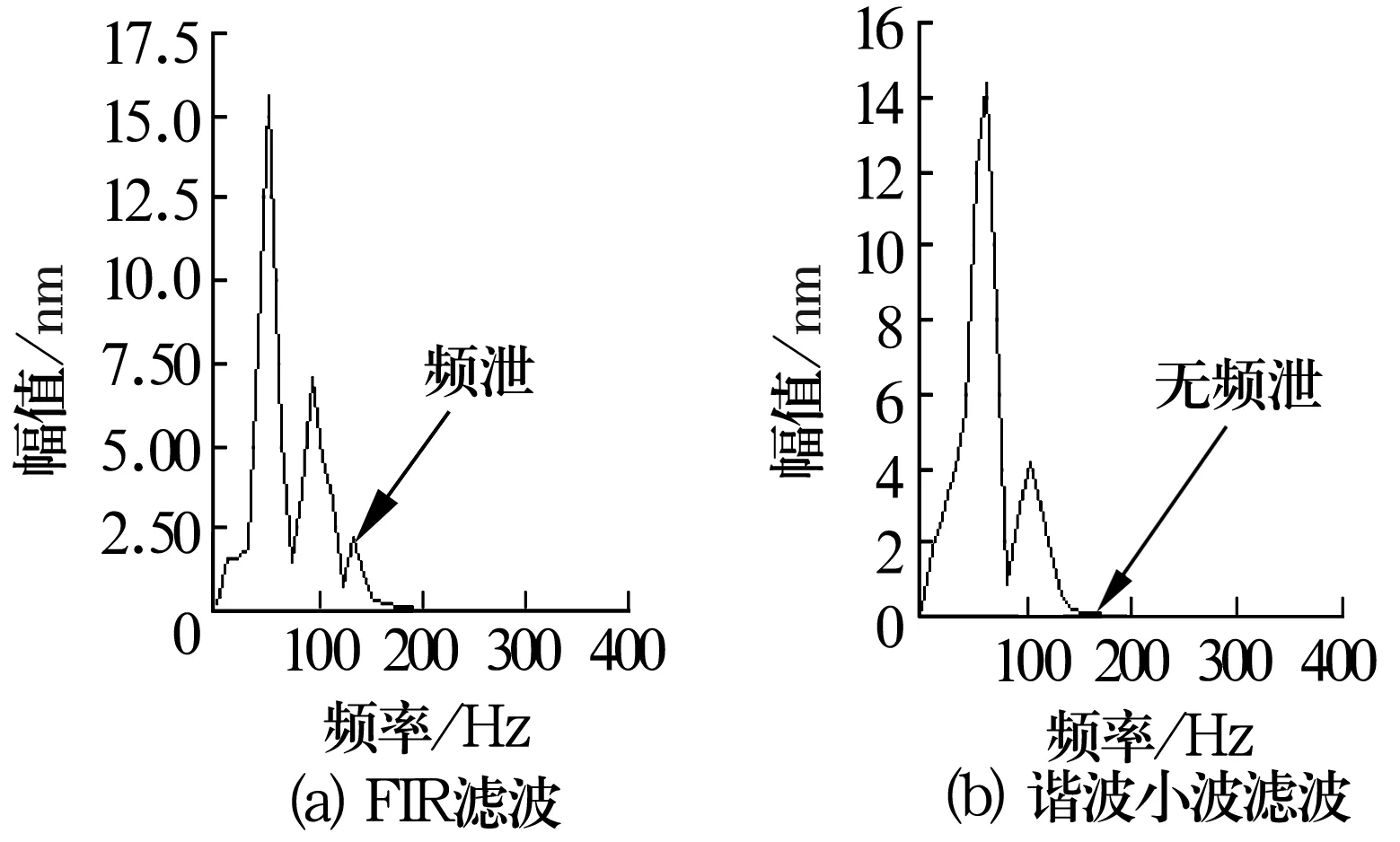
图7 油膜振荡滤波信号幅值谱
由图可知,经谐波滤波后信号的幅值谱光滑度提高,不规则度减小。进一步分析发现,油膜涡动的幅值谱中涡动频率成分出现在27 Hz,而工频成分出现在58 Hz,涡动频率约为工频的0.47倍。油膜振荡的幅值谱中涡动频率成分出现在56 Hz,而工频成分出现在107 Hz,涡动频率近似为转子的一阶临界转速(3 500 r/min),涡动频率对应的幅值高于工频对应幅值的2倍,满足油膜涡动与振荡的理论分析。同时发现,谐波小波滤波比FIR滤波所得频谱图的频泄现象小很多,这是由于谐波小波具有盒形特征,不存在泄漏或泄漏问题比较小,从而可以更加准确地判断油膜涡动与振荡的特征频谱信息。
油膜涡动与振荡发生时,轴心轨迹也是故障特征判断的重要依据。油膜涡动与振荡的轴心轨迹分别如图8、图9所示。
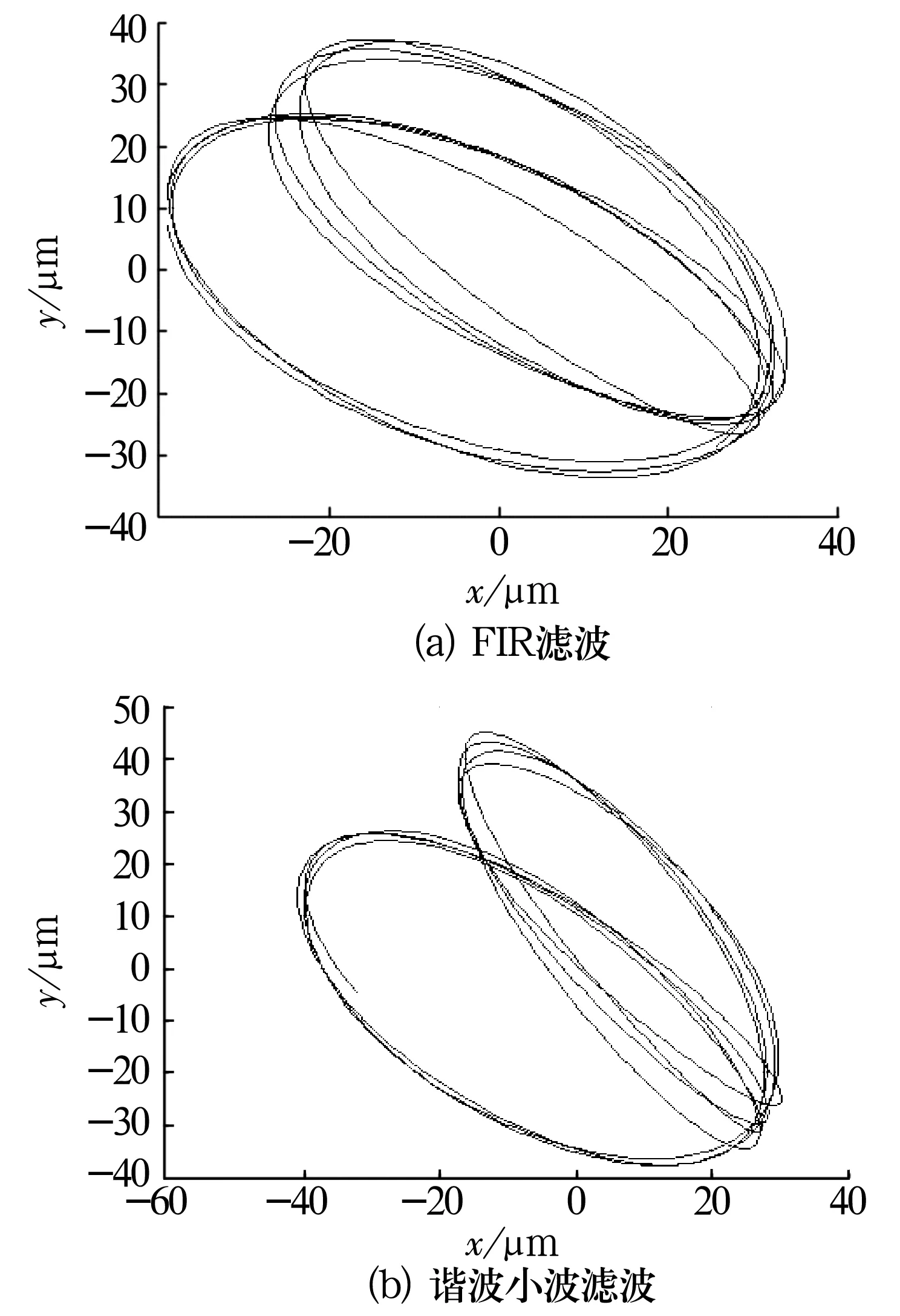
图8 油膜涡动轴心轨迹图
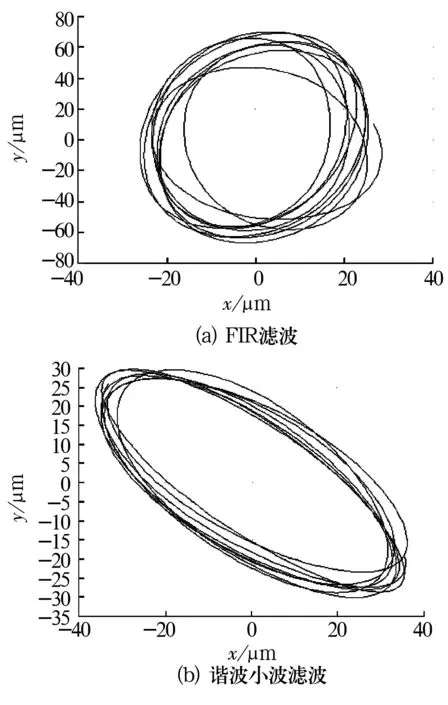
图9 油膜振荡轴心轨迹图
由图可知,当滑动轴承在转动过程中出现油膜涡动时,轴心轨迹会呈现规则的大环套小环特征;发生油膜振荡时,对应的轴心轨则不规则。分析发现,经谐波小波滤波的轴心轨迹比经FIR滤波的轴心轨迹图更加平滑,更符合涡动与振荡的实际轨迹,说明谐波小波滤波在处理非平稳非线性振动信号时比FIR滤波更具优势。
4 结论
利用谐波小波对轴承的油膜涡动与振荡故障信号进行滤波与处理,所得结果更具优势:
(1)从理论算法看,谐波小波是复小波,具有实部和虚部,所以无论信号谐波频率成分的相位如何,经小波变换后均可得到各个谐波频率成分,且存在确定的函数表达式,算法实现更加简单。
(2)谐波小波变换具有良好的时频局部化特性,使其在时频面上的定位更加精确, 同时也提高了信号与背景的对比度。
(3)谐波小波具有良好的频域盒形谱特性,在滤波过程中无频泄现象或频泄较小。能得到更加精确的轴心轨迹,不需要其他提纯处理。
(4)谐波小波同时提供了一些其他小波分析结果所缺少的信息,如对任意频段进行细化分析,而且在各频带中仍然具有与原始信号相同的频率分辨率,这些更加有效地解决了非稳态非线性机械设备的状态监测和诊断问题,弥补了传统滤波方法的不足。故利用谐波小波变换进行油膜涡动与振荡故障识别更加有效、准确。

