无轴承永磁同步电动机径向力模型

李可，孙晓东，杨泽斌

(江苏大学 a.电气信息工程学院；b.汽车工程研究院，江苏 镇江 212013)

无轴承永磁同步电动机(bearingless permanent magnet synchronous motor，BPMSM)具有体积小、重量轻、效率高、功率因数高、控制特性好等优点，还具有磁轴承无摩擦、无磨损、不需润滑、高转速和高精度等优点，因此在航空航天、生物医药、半导体制造等特殊领域具有广泛的应用前景[1-5]。

为了保证BPMSM的稳定悬浮运行，必须对径向力进行实时控制，因此径向力的精确计算是电动机本体设计和控制策略研究的基础。文献[6]对表贴式BPMSM的数学模型进行试验研究，在得到电感系数的前提下，采用虚位移原理确定了BPMSM径向力模型，该方法必须依赖试验数据，因此计算较为复杂，影响径向力模型的准确性。文献[7-8]分别对插入式、埋入式BPMSM的数学模型进行了深入研究，首先得到转矩和悬浮两套绕组交链的磁链方程，在此基础上求得电磁能方程，再根据虚功原理求得径向力方程。文献[6-8]对BPMSM的径向力模型进行研究时并没有对转子偏心情况下的径向力进行深入分析研究，是一种比较理想的径向力方程，但在实际运行过程中，BPMSM定转子之间的偏心是存在的。针对现有模型的不足，结合麦克斯韦张量法及磁路法，建立考虑偏心位移的BPMSM径向力模型，并运用有限元分析对其进行仿真。

1 BPMSM径向力产生原理

BPMSM定子中叠绕着转矩绕组和悬浮力绕组，由于悬浮力绕组产生的磁场打破了原有转矩绕组(包括永磁体，下同)建立的气隙磁场的平衡，从而产生作用在转子侧的径向力。设BPMSM的悬浮力绕组和转矩绕组的极对数分别为PB和PM(下标B，M分别表示悬浮力绕组和转矩绕组的相关参数)，BPMSM要同时实现稳定旋转和悬浮运行，必须满足3个条件：(1)两套绕组的极对数相差1，即PB=PM±1；(2)两套绕组产生的旋转磁场方向相同；(3)通入两套绕组中的电流频率相同[9]。

BPMSM的径向力产生原理如图1所示。图中，PM=1且PB=2；NBa和NBb为悬浮力绕组，NMa和NMb为转矩绕组，两者叠压在BPMSM的定子槽中。悬浮力绕组通电后产生四极气隙磁通Ψ4，原本由永磁体产生的二极磁通Ψ2的平衡被四极气隙磁通Ψ4打破，由于气隙磁通的不均匀分布进而产生径向力。如果BPMSM转子位于中心位置，二极气隙磁通Ψ2主要由BPMSM转子表面的永磁体产生，当BPMSM空载悬浮运转，对应的转矩绕组中的电流很小，由转矩绕组电流产生的磁通可以忽略不计。如果NBa和NBb中不通入电流，二极磁通Ψ2保持平衡，此时径向力为0。当绕组NBa中通正向电流，产生的四极气隙磁通Ψ4使转子右侧气隙1处磁通密度增加，转子左侧气隙3处磁通密度减小，从而产生沿x轴正方向的径向力；当绕组NBa中通反向电流，则会产生沿x轴负方向的径向力。同理，沿y轴方向的径向力可以通过在绕组NBb中通入电流获得。因此，通过控制悬浮力绕组NBa和NBb中的电流就可以控制悬浮力的大小和方向，从而实现转子的稳定悬浮。

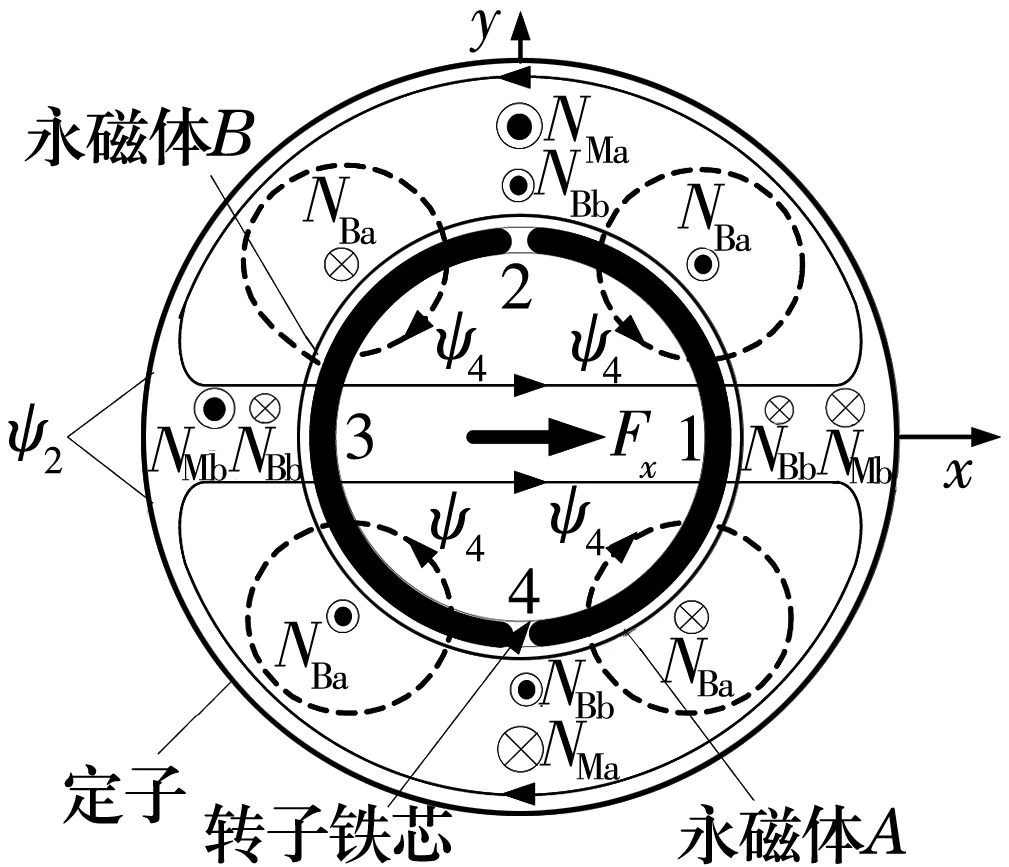
图1 径向力产生原理

2 径向力模型

根据麦克斯韦张量法，BPMSM转子表面dS面积上沿机械角θ受到的法向力和切向力分别为[10]

(1)

bt(θ,t)=-Btcos(ωt-PMθ-γM)，

(2)

式中：bn(θ,t)和bt(θ,t)分别为转矩绕组和悬浮力绕组的合成气隙磁密的法向和切向分量；θ为沿定子内表面逆时针机械角度；μ0为真空磁导率；Bt为切向气隙磁密幅值；γM为PM对极气隙磁动势基波的空间初始相位角；ω为电角频率。

由(1)式可得径向力在α和β方向上的分量为

，(3)

式中：r为转子外半径；l为转子铁芯有效长度。

BPMSM定、转子之间偏心位移如图2所示。图中，O′(α,β)为偏心转子轴心的坐标；g0为BPMSM定、转子之间的平均气隙长度；R为定子的内半径。定、转子之间的气隙长度g(θ)为

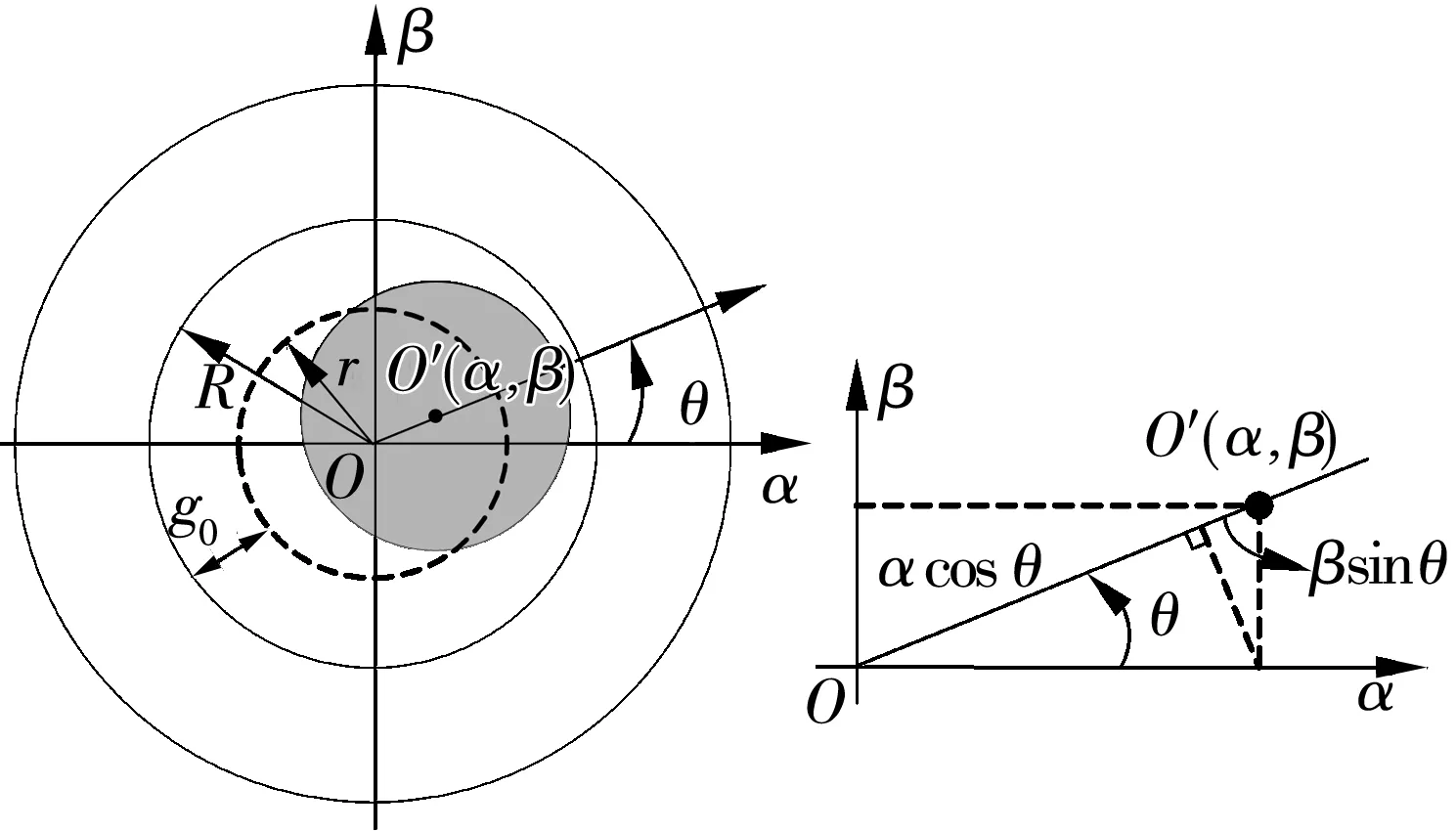
图2 转子偏心位移

g(θ)=g0-g1=g0-(αcosθ+βsinθ)，

(4)

式中：g1为定、转子之间的偏心气隙长度；α和β分别为转子沿α和β方向的径向位移。

由于BPMSM在稳定悬浮工况下运转，定、转子之间的偏心气隙长度g1与平均气隙长度g0相比较小，因此可以忽略，则气隙长度倒数为

(5)

单位面积内的气隙磁导分布函数为

(6)

由BPMSM中PM对极转矩绕组电流与转子永磁体磁场共同建立的合成气隙磁动势的基波分量，以及PB对极悬浮力绕组建立的气隙磁动势的基波分量分别为

(7)

式中：FM，FB分别为PM对极和PB对极气隙磁动势基波幅值；γB为PB对极气隙磁动势基波的空间初始相位角。由两套绕组共同产生的气隙磁通密度分别为

(8)

从而可得BPMSM气隙磁密的法向分量为

bn(θ,t)=bM(θ,t)+bB(θ,t) 。

(9)

假设均匀气隙下PM对极和PB对极气隙磁通密度幅值分别为

(10)

式中：NM，NB分别为转矩绕组和悬浮力绕组每相串联有效匝数；IM，IB分别为转矩绕组励磁电流(包括转子永磁体激励的磁场等效至转矩绕组中的电流部分)和悬浮力绕组电流幅值。

将(2)式和(8)式代入(3)式进行积分，可得α，β方向上转子受到的径向力。考虑到径向位移α和β，以及气隙磁通密度幅值BM的数值较小，故忽略其平方项，可得

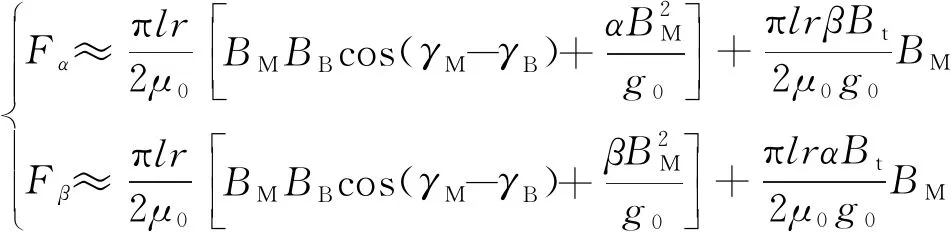
。(11)

转矩绕组每相气隙磁链值为

(12)

又有

ψM=LMIM，

(13)

式中：ΦM为每相气隙磁通值；LM为转矩绕组互感。则(11)式可以化简为

(14)

由(14)式可知，BPMSM的径向力由3部分组成：(1)不计偏心时，由转矩绕组气隙磁场与悬浮力绕组电流相互作用产生的可控径向力(径向力的主要组成部分)；(2)定、转子偏心引起的单边磁拉力；(3)由于气隙磁密沿气隙圆周在转子表面切向分布不均而产生的径向力。

3 仿真与分析

为了验证所建径向力模型的正确性和有效性，采用有限元方法进行仿真分析。有限元分析参数采用试验样机参数：定子外径140 mm，定子内径77 mm，转子外径75 mm，永磁铁厚度2 mm，定子槽数24，气隙1 mm，铁芯长度100 mm，悬浮力绕组匝数80，转矩绕组匝数80，永磁铁剩余磁感应强度1.2 T，矫顽力900 kA/m，转矩绕组极对数2，功率2 kW，电动机气隙2 mm，36槽，电动机转矩绕组电阻3.24 Ω，直轴和交轴电感0.012 H，转动惯量0.015 8 kg·m2，悬浮力绕组极对数3，悬浮力绕组电阻2.32 Ω，辅助机械轴承气隙0.5 mm。

转矩绕组电流为额定值3 A，悬浮力绕组电流分别为1，3和5 A，且定、转子在x轴方向偏心位移为α时，径向力与悬浮力绕组电流的关系如图3所示。

由图3可知，径向力的理论计算值直线的斜率均相同，即当定、转子偏心的变化量相同时，径向力的变化量也相同，说明当转矩绕组和悬浮力绕组中通入的电流大小一定时，由于机械轴承气隙(最大可偏距离)远小于电动机气隙，径向力与定、转子偏心之间的非线性关系不明显，可近似为线性关系。当定、转子在x轴方向偏心时，x方向径向力的变化要比y方向径向力的变化显著，说明x方向的偏心主要影响x方向的径向力。当电流较小(磁路未严重饱和)时，径向力的有限元计算值与理论值非常吻合，随着磁路达到饱和，径向力的有限元计算值虽然开始偏离理论值，但是两者基本吻合，说明考虑定、转子偏心位移的径向力模型能够较为准确地描述BPMSM的径向力。

图3 x方向偏心时径向力与悬浮力绕组电流关系

4 结束语

在对BPMSM径向力进行深入分析的基础上，运用麦克斯韦张量法和磁路法，建立了一种较为精确的BPMSM径向力数学模型。该模型充分考虑了定、转子偏心位移，为BPMSM悬浮运行控制的研究和电动机本体设计提供了可靠的理论依据。利用有限元分析方法验证了该模型的计算精度，为进一步深入研究BPMSM高精度的控制系统打下了基础。