基于改进型GDQ法FGM纳米梁的热-机耦合振动及屈曲特性分析

周凤玺， 蒲 育，2

（1.兰州理工大学 土木工程学院，兰州 730050；2.兰州工业学院 土木工程学院，兰州 730050）

近些年，随着微纳米测试与微机械加工技术的迅猛发展，许多材料力学试验已表明:微/纳米结构的静动态力学特性均表现出显著的尺度效应。Eringen[1]非局部弹性理论含有1个内禀尺度效应参数，很好地解释了尺度效应，从而基于该理论对微/纳结构力学特性分析及应用日益广泛[2]。功能梯度材料（functionally graded material，FGM）微/纳米梁模型以其简单而高效的结构形式，FGM优异的热稳定性、可设计性与智能可控性等，目前常见于微机电系统（micro-electromechanical-systems，MEMS）中的核心组件，诸如微执行器、微传感器、微谐振器等。分析此类微/纳结构的力学特性关乎MEMS核心组件的安全与设计、功能与优化、智能与控制等，这也是复合材料纳米力学优先发展的前沿课题，因而备受学者们关注。

基于Eringen非局部弹性理论，Thai[3]采用一种抛物线型剪切梁理论，应用Navier法分析了简支纳米梁的弯曲、屈曲及自由振动。Ke等[4]基于Timoshenke梁理论（first-order shear deformation beam theory，FSBT），采用微分求积法（differential quadrature method，DQM）研究了压电纳米梁的热-机-电耦合振动特性。文献[5-6]考虑了各向同性材料，均采用Euler-Bernoulli梁理论（classical beam theory，CBT），刘灿昌等研究了纳米梁的非线性振动问题，张大鹏等利用传递函数法分析了黏弹性地基上纳米梁的振动特性。Rahmani等[7]基于FSBT并采用Navier法，首次研究了FGM纳米简支梁的自由振动，其结果表明:尺度效应对FGM纳米梁的固有频率影响显著，纳米尺度因子越大，则频率越低。Ebrahimi等[8-11]考虑了不同温度分布类型下材料物性随温度变化的相关性，采用CBT，FSBT并应用Navier法及微分变换法（differential transform method，DTM），先后研究了FGM纳米梁的挠曲振动、热-机耦合振动、热屈曲问题。最近，文献[12-14]均采用CBT，Ebrahimi等[12]应用DTM数值研究了FGM纳米梁的湿-热-机耦合振动特性；Hosseini等[13]应用Navier法获得了FGM纳米简支曲梁自由振动响应的精确解；Nejad等[14]应用广义微分求积法（generalized differential quadrature，GDQ）数值研究了双向FGM纳米梁的屈曲特性，但未考虑热环境工况。Ansari等[15]基于FSBT考虑了几何非线性，将Newton-Raphson迭代法和GDQ法相结合，数值研究了压电FGM纳米梁在热-机-电耦合作用下的非线性自由振动问题。Ebrahimi等[16]基于Reddy三阶剪切梁理论（third-order shear deformation beam theory，TBT），考虑了微孔隙的影响，应用Navier法研究了弹性地基上压磁/电FGM纳米简支梁的磁-电耦合振动特性。

综上所述，目前针对热-机耦合作用下FGM纳米梁振动与屈曲特性的研究仍十分有限，且这两类问题都需要求解复杂耦合微分方程组的特征值问题，获得解析解十分困难，故大多只限于简支梁而采用Navier法获得精确解。其次，为了将研究问题简化分析，大多学者采用了CBT模型，由于该梁理论忽略了剪切作用的影响，故而由此预测的FGM纳米梁静动态响应其精确性仍有待商榷。此外，已有文献对热-机耦合作用下FGM纳米梁屈曲与振动这两类静动态力学行为耦联性的揭示目前十分少见，仍需进一步研究。

本文采用n阶广义梁理论（generalized beam theory，GBT）[17]，基于非局部线弹性理论，在Hamilton体系下统一建立热-机耦合FGM纳米梁的振动与屈曲控制方程。应用前期研究基础之上提出的一种改进型广义微分求积法（modified generalized differential quadrature，MGDQ）[18-19]求解动态响应，通过屈曲与振动这两类力学行为之间的二元耦联性，编写相应的循环子程序用来求解屈曲静态响应。通过算例刻画了多参数（因素）共同对FGM纳米梁振动及屈曲特性的影响，分析了其影响作用机理。

1 控制微分方程

1.1 材料属性

如图1所示，一长宽高分别为L×b×h的FGM纳米梁，上表面为纯陶瓷，下表面为纯金属。梁受初始轴向机械载荷为N（假设压力为正），考虑温度T沿梁的厚度方向温态分布，材料的物性沿梁厚按Voigt混合幂律呈梯度分布且依赖于温度变化。弹性模E，热膨胀系数α，热传导率κ，泊松比υ，密度ρ等物性参数均是坐标z和温度T的函数，可用统一式表示为

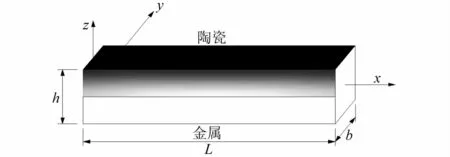
图1 FGM纳米梁的几何尺寸Fig.1 Geometry of a FGM nanobeam

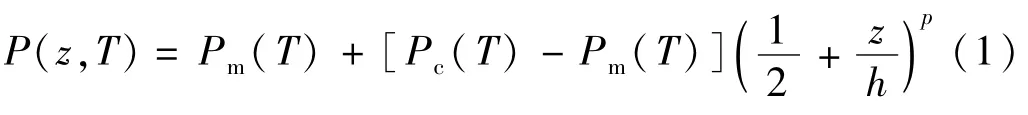
式中:Pm（T）和Pc（T）分别为金属与陶瓷材料与温度相关的某一物性参数；p为FGM纳米梁材料组分的梯度指标。显然，当p=0时，FGM退化为纯陶瓷材料；当p=∞时，退化为纯金属材料。Pm（T）和Pc（T）随温度T的变化可统一表述为

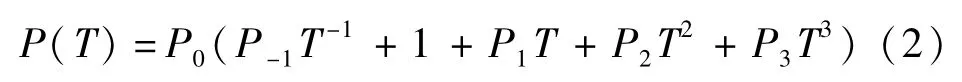
式中，Pi（i=-1，0，1，2，3）为与温度相关的材料系数。表1给出了金属（SUS 304）和陶瓷（Al2O3）这两种材料与温度相关的材料系数[20]。

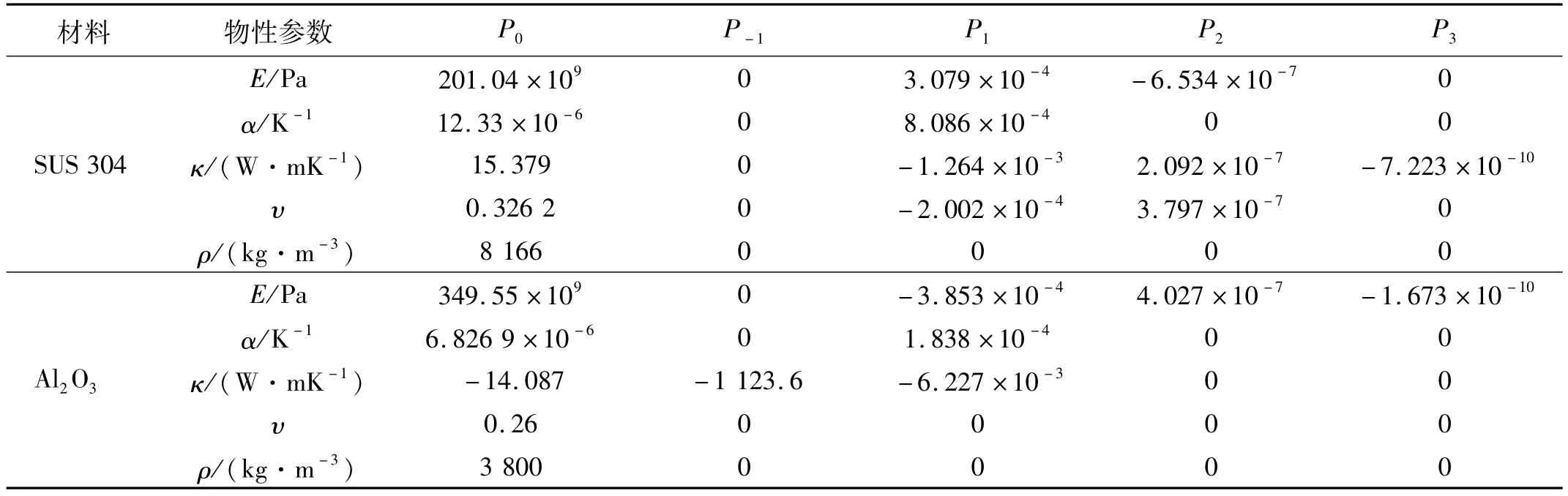
表1 金属（SUS 304）和陶瓷（Al2 O3）两种材料随温度变化的物性系数Tab.1 Temperature-dependent coefficients for metal（SUS304）and ceramic（Al2 O3）

1.2 升温类型

本文考虑以下3种升温类型:

类型1——均匀升温（uniform temperature rise，UTR）

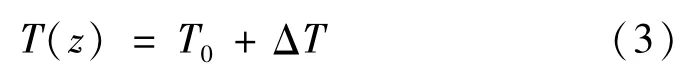
式中:T0为无应力状态时的参考温度，本文取T0=300 K；ΔT为升温值。

类型2——线性升温（linear temperature rise，LTR）

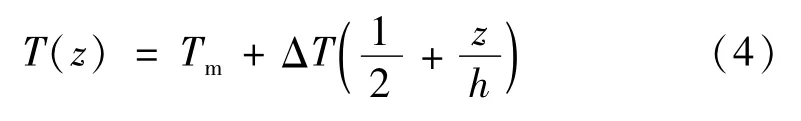
式中，ΔT=Tc-Tm。

类型3——非线性升温（non-linear temperature rise，NLTR）

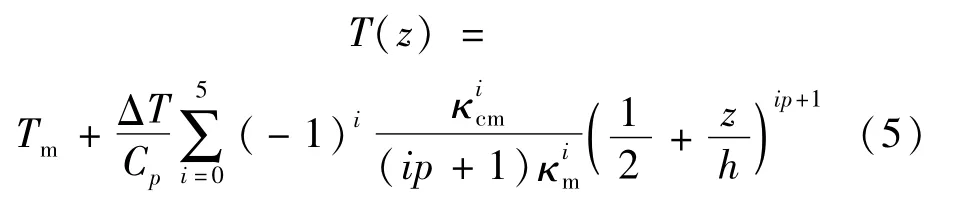
1.3 运动方程

梁内任意一点在t时刻沿x，y，z方向的位移分量可描述为

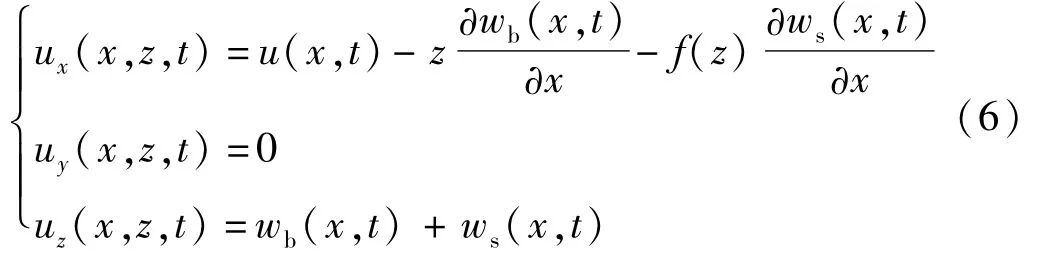
式中:u（x，t），wb（x，t），ws（x，t）分别为梁轴线上一点的轴向位移、弯曲变形项挠度及剪切变形项挠度；f（z）=h（2z/h）n/（2n）为n阶广义梁理论对应的横向切应力形函数。显然，GBT可退化为3种著名的梁理论:当n=1时，退化为CBT；当n=3时，退化为TBT；当n=∞时，退化为FSBT。

由线弹性小变形的几何方程可得非零应变分量

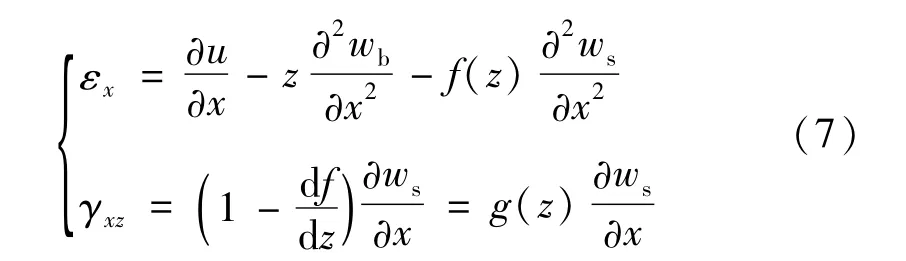
式中，g（z）=1-f′（z）为横向切应变形函数。

由Eringen非局部线弹性理论，本构方程为

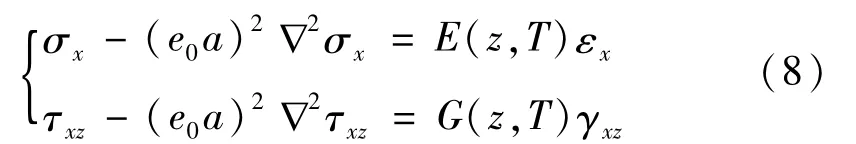
式中:e0为材料的非局部常数；a为内部特征长度；μ=（e0a）2定义为尺度效应非局部参数；L为外部特征长度；G（z，T）为剪切模量；∇2为一维Laplace算子。

结构动能的变分

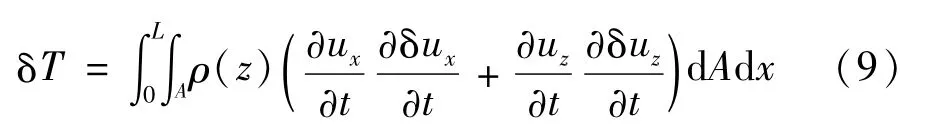
结构应变能的变分

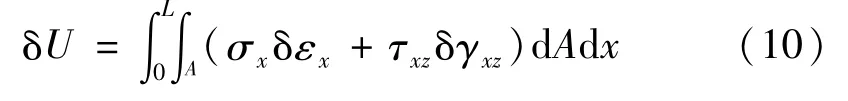
初始轴向机械载和热载荷做功的变分

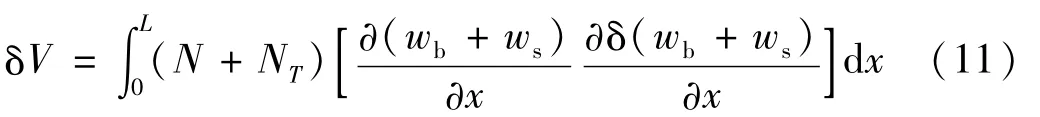
对系统应用Hamilton原理

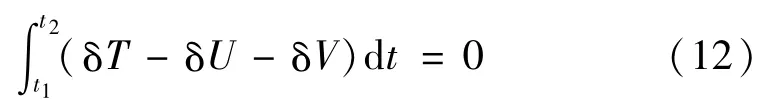
将式（7）～式（11）代入式（12）并作一些变分和积分运算，化简后可得运动方程及边界条件

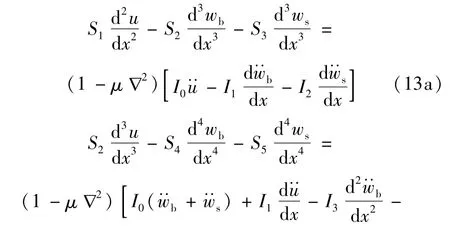
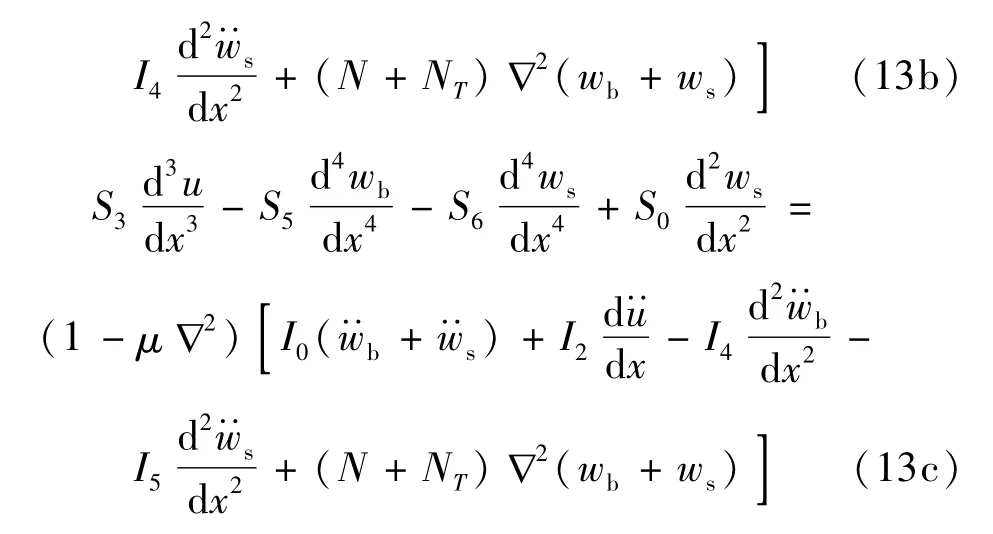
显然，当式（13）中与时间t无关时，则问题退化为FGM纳米梁的热-力耦合屈曲方程。此外，需要指出，严格意义上来讲，Hamilton原理导出的边界条件为尺度效应相关的非局部边界条件，但基于Saint-Venant原理，可略去梁左右两端小边界处尺度效应相关的高阶微量，进而经简化并化简后，考虑以下3种梁边界:

（i）左端固支-右端固支（C-C）

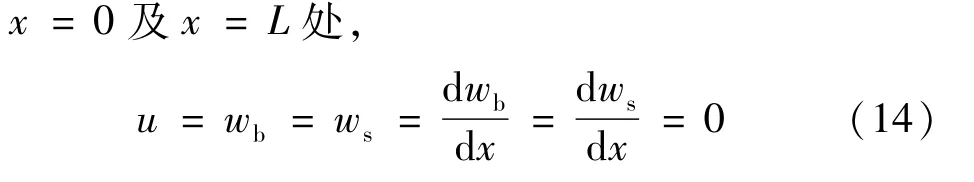
（ii）左端简支-右端简支（S-S）

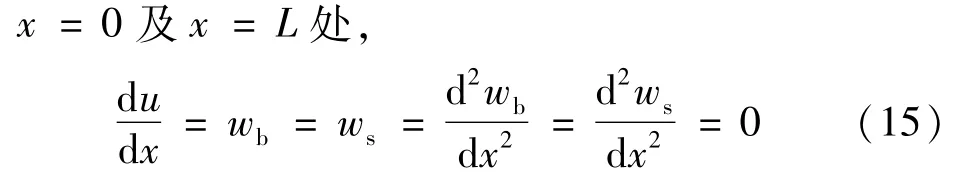
（iii）左端固支-右端简支（C-S）

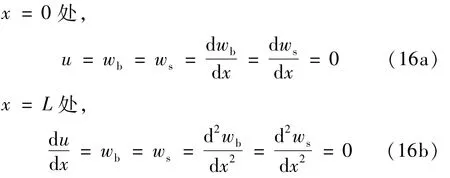
1.4 振动控制微分方程

自由振动为简谐运动，位移分量可设为

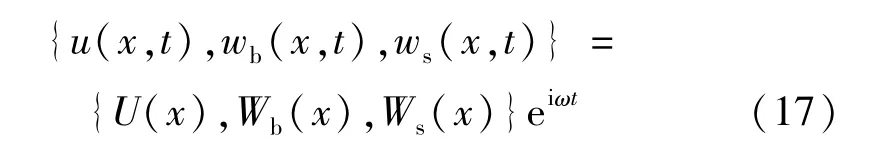
式中:U（x），Wb（x），Ws（x）为振型函数；ω为振动频率；i为虚数单位。

将式（17）代入运动方程式（13）可得FGM纳米梁热-机耦合振动的控制微分方程

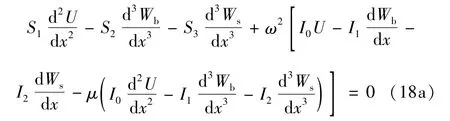
2 MGDQ法与特征值问题

首先，GDQ实施离散化前，不失一般性，各参数采用如下的无量纲化

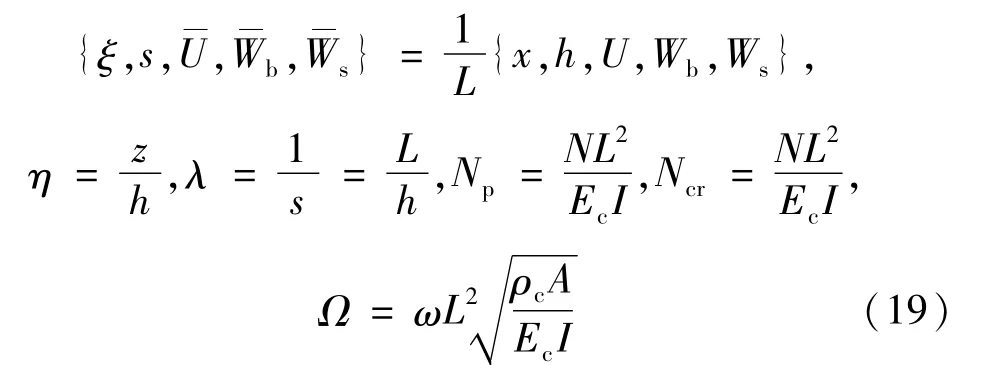
式中:λ为梁的跨厚比；I为惯性矩；Np和Ncr分别为无量纲初始轴向机械载荷和临界屈曲载荷；Ω为无量纲频率。

2.1 引入边界控制参数

通过引入边界控制参数，可实施C-C，C-S，S-S这3种边界FGM纳米梁动态响应MGDQ法求解的MATLAB统一化编程，达到优化数值方法的目的。首先，基于GDQ法，位移振型函数在离散节点ξ=ξi处的k阶导数可表示为

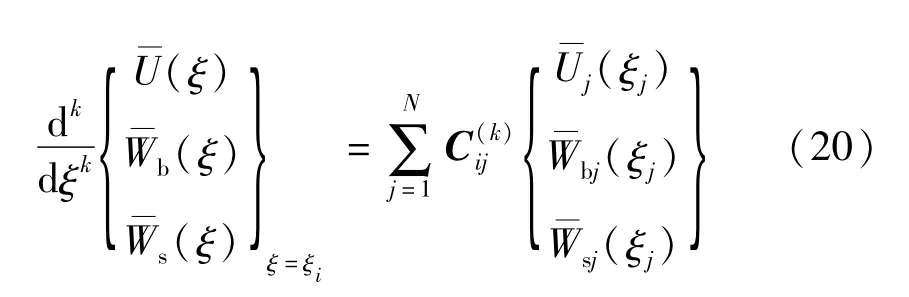
其次，可定义ξ=0及ξ=1处任意未知函数0阶导数的权系数

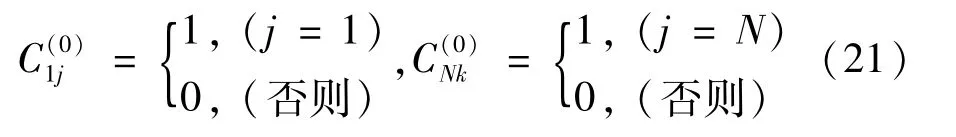
据此定义，纳米梁的3种边界条件方程式（14）～式（16）可由GDQ统一离散化为

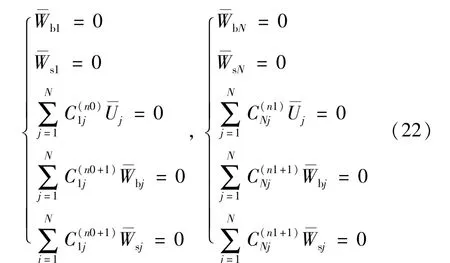
式中:n0=0或1；n1=0或1；n0和n1为边界条件控制参数；n0=0，n1=0为C-C梁；n0=0，n1=1为CS梁；n0=1，n1=1为S-S梁。

2.2 MGDQ法的无量纲离散方程

考虑到应用传统的GDQ离散控制方程与边界方程后，方程总数和节点振型位移未知量的数目不相等，不能直接将振动问题转化为特征值问题求解其动态响应。因此本文在前期研究基础之上，采用一种改进型GDQ法进行求解。即从离散边界条件方程式（22）出发，消去边界点处的6个节点位移，同时解出内点处的这4个节点位移，使控制方程离散数目与振型位移独立未知量的数目相等。其改进型权系数矩阵具体推导可参考蒲育等的研究。

将无量纲式（19）代入控制方程式（18）并应用MGDQ法离散后可得3种边界下FGM纳米梁热-机耦合振动的统一化无量纲离散线性方程组

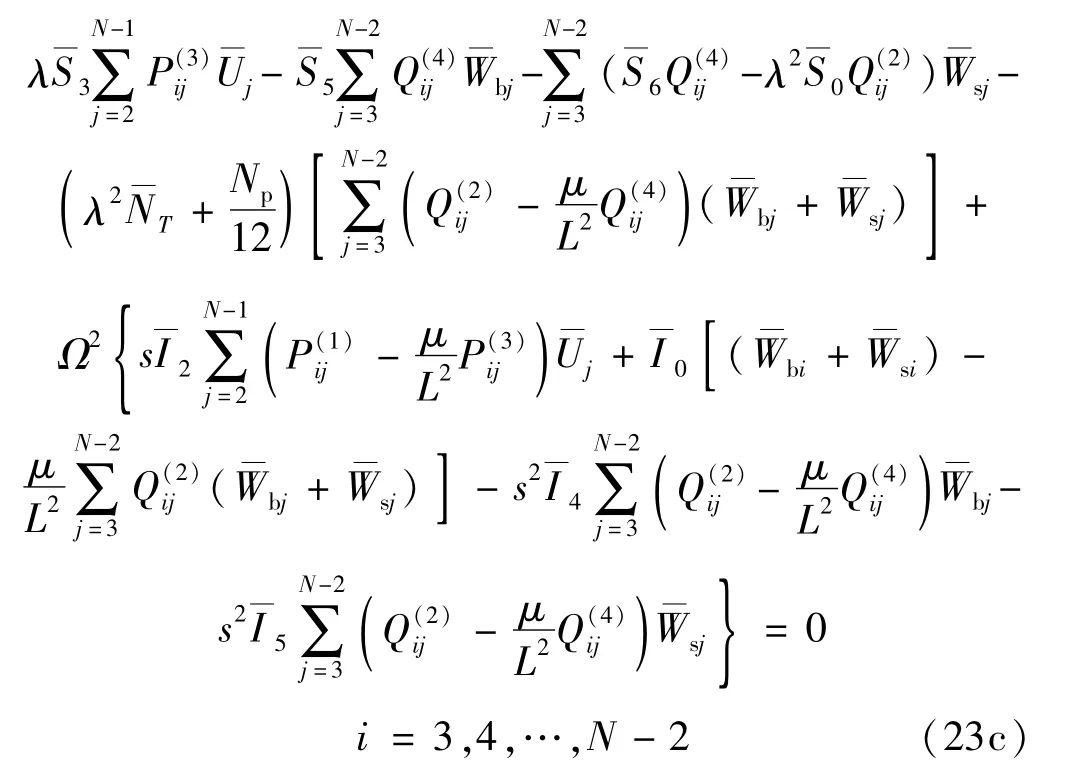
2.3 振动与屈曲两类问题的特征值

线性代数方程式（23）可用分块矩阵表示为

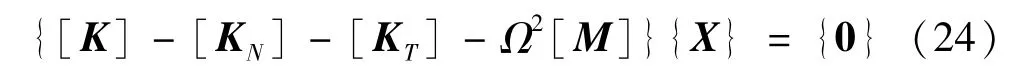
式中:[K]与[M]分别为弹性刚度矩阵与质量矩阵，且均为（3N-10）阶方阵；[KN]与[KT]分别为轴向机械载荷及热载荷作用对应引起的子刚度矩阵；{X}为独立节点振型位移列向量，其表达式为

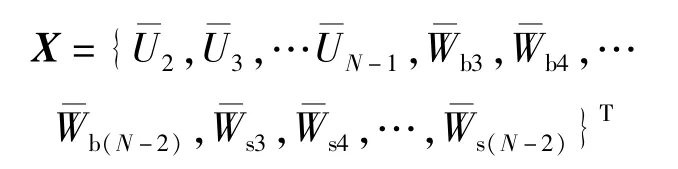
显然，求解线性方程式（24）的特征值问题可获得FGM纳米梁热-机耦合振动的频率和相应的振型。通过振动与屈曲的二元耦联性，编写MATLAB循环子程序可求解得出临界屈曲载荷、热屈曲及热-力耦合屈曲临界升温值、临界跨厚比等重要参数指标。

3 算例分析与讨论

3.1 GBT阶数n值的探讨及结果的有效性

本文取离散节点个数N=17，纳米梁的长宽尺寸分别为L=104nm，b=103nm，非局部参数采用 μ×10-6（nm）2的形式表示量级和量纲。本节主要探讨不同梁理论对FGM纳米梁预测频率的影响并对数值结果的有效性进行验证。

表2给出了均匀升温（UTR）热载荷作用下C-C，C-S及S-S这3种边界FGM纳米梁（λ=20，μ=1，ΔT=20 K）的前三阶无量纲频率Ω并与文献[9]的结果进行了比较。本文采用TBT（n=3），而文献[9]为了简化分析采用了CBT（n=1）。不难看出:两者预测的基频结果比较吻合。注意到算例中跨厚比λ=20为细长梁，故而两种梁理论预测的基频结果比较接近。但随着振型阶数的增加，对三阶无量纲频率Ω3值而言，文献[9]的结果明显偏高。这是由于CBT忽略了剪切变形作用的影响而高估了梁的整体刚度。换言之，即使对于纳米尺度细长梁而言，CBT比TBT预测的高阶频率值也明显偏高。此外，由表2可见:约束越强，相应的频率值越大；梯度指标p越大，频率值越小。

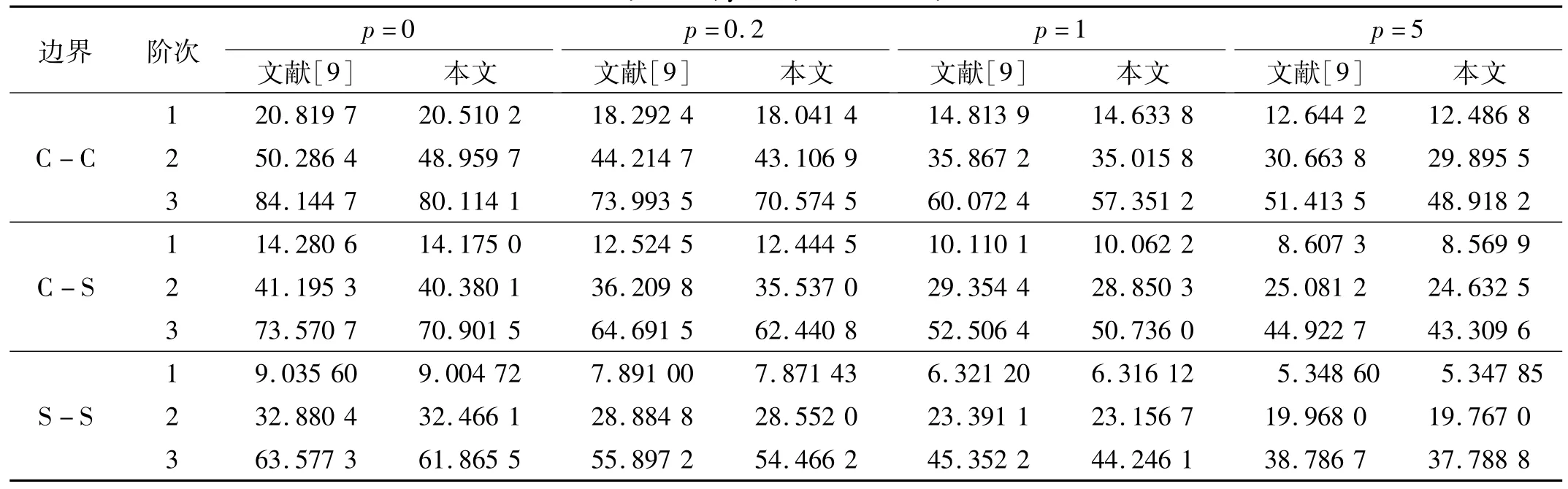
表2 不同边界FGM纳米梁均匀升温下的前三阶无量纲频率（λ=20，μ=1，ΔT=20 K）Tab.2 First three dimensionless frequencies of FGM nanobeams under the UTR for different boundary conditions（λ=20，μ=1，ΔT=20 K）

图2主要用于验证并探讨GBT阶数n的理想取值。考虑了UTR热载荷作用，图2（a）～图2（c）分别给出了FGM纳米固支梁（p=1，μ=1，λ=20，ΔT=40 K）的前三阶无量纲频率Ω随GBT阶数n变化的关系曲线:总的来看，各阶频率Ω都随n的变化波动很小，n取偶数略微高于n取奇数（除n=1外）时预测的频率，随着n的增加，各阶Ω值趋于稳定，将趋于FSBT预测的频率值。n=2时各Ω值为最大，n=3时（TBT）各 Ω值为最小，n=1（CBT）预测的频率值介于期间。需要指出，取n=1实施计算过程中，结果显示刚度矩阵奇异，此时可取n≈1代替（如取n=1.001），将此作为退化的CBT。与文献[9]CBT预测的相应频率值Ω1=14.513 1，Ω2=35.406 4，Ω3=59.492 1进行比较:由图2可见，本文退化的CBT预测各阶频率值均偏低，且更为接近高阶剪切梁理论TBT的预测值。

图2 UTR升温下FGM纳米固支梁的前三阶无量纲频率Ω与GBT阶数n的关系曲线Fig.2 First three dimensionless frequencies of a C-C FGM nanobeam under the UTR versus orders of n for the GBT

综上所述，本文所采用的MGDQ法切实可行，行之有效。另一方面，即使对于纳米尺度细长梁而言，CBT比TBT预测的高阶频率值也明显偏高。因此，为使在高频振动中获得精确的输出响应、同时也便于工程中使用，建议GBT的阶数取n≥3的奇数为宜。

3.2 FGM纳米梁的耦合振动及耦合屈曲特性

本节采用TBT，主要探讨FGM纳米梁的热-机耦合振动及屈曲特性。图3（a）～图3（c）分别刻画了C-C，C-S，S-S这3种边界FGM纳米梁（p=1，λ=20）的Ω1-Np关系曲线:无量纲基频Ω1都随无量纲轴向机械压力Np的增加而单调减小，直至达到各自临界屈曲载荷Np=Ncr时而发生失稳，此时Ω1=0。换言之，由Ω1-Np曲线与横轴交点的坐标值可确定Ncr值。这是由于轴向机械压力削弱了梁结构的整体刚度，当Np=Ncr时，FGM纳米梁达到屈曲状态而发生临界失稳，由于临界失稳为静平衡状态，故而Ω1=0。这也反映了FGM纳米梁屈曲和振动这两类静动态力学行为之间的转化和二元耦联性。本文基于该二元耦联性，通过编写相应的MATLAB循环子程序用以求解FGM纳米梁屈曲静态响应，这样可避免屈曲问题求解的二次解耦，二次提高计算效率。此外，由图3可见:对μ=0，μ=1，μ=2，μ=3，μ=4这5种取值而言，非局部参数μ值越大，基频Ω1和临界载荷Ncr越小。这是由于μ值越大，则尺度效应越显著，纳米梁的整体刚度将明显弱化的缘故。比较图3（a）～图3（c）可见:取相同的参数值，约束越强，频率和临界载荷值越大，则纳米梁越不易失稳。这与宏观尺度（μ=0）FGM梁类似，边界约束强，梁抵抗变形的能力就强，进而抗失稳能力也就提高了。

图3 不同边界下FGM纳米梁的无量纲基频Ω1与无量纲初始轴向压力N p的关系曲线Fig.3 Curves of dimensionless fundamental frequencyΩ1 of FGM nanobeams versus dimensionless initial axial compressive force N p for different boundary conditions

为了便于下文分析不同升温类型对FGM纳米梁频率和临界载荷的影响及作用机理，考虑了UTR，LTR，NLTR这3种升温类型，图4给出了FGM纳米梁（p=1）的拉/压弹性模量系数S1随升温ΔT的变化关系:各S1值均随ΔT的增加而单调减小。取相同的ΔT值，UTR使S1减小最为显著，LTR次之，NLTR最为不明显。其余弹性模量系数Si与之类似，这里不再一一验证。换言之，由于本文考虑了材料物性与温度的相关性，对这3种温度分布升温类型而言，梁结构的弹性刚度均随升温ΔT的增加而降低了，且UTR使其减小最为明显，NLTR使其减小最为缓和，进而UTR使频率和临界载荷减小最为显著。

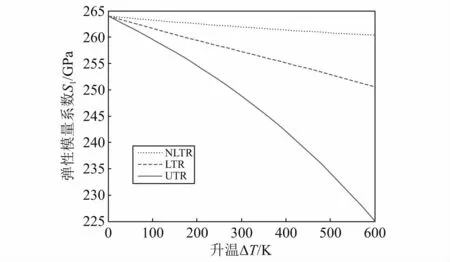
图4 不同升温类型下弹性系数S1与升温ΔT关系曲线Fig.4 Curves of elastic coefficient S1 versus different types of temperature riseΔT

图5（a）、图5（b）分别给出了UTR和LTR升温下3种边界FGM纳米梁（p=1，μ=1，λ=20）的Ω1-ΔT和Ncr-ΔT关系曲线:各基频Ω1和临界载荷Ncr曲线值均随升温ΔT的增加而单调减小，直至达到各自的临界升温值ΔTcr时发生热屈曲而失稳，此时Ω1=0，Ncr=0，两类曲线与横轴交点的坐标值几乎相同，该值即为相应的ΔTcr。这是由于随着ΔT的增加，各弹性系数减小了，进而结构的弹性刚度降低了；另一方面，增大的热轴力为压轴力，这也愈加削弱了梁结构的整体刚度，当ΔT=ΔTcr达到热屈曲状态时，临界失稳载荷完全由热轴力提供，不需要额外的轴向机械压力，故而Ncr=0，且热屈曲为临界平衡状态，从而Ω1=0。这也再次表明了FGM纳米梁两类静动态力学行为之间的二元耦联性。此外，取相同的ΔT值时，同一边界下UTR比LTR使Ω1和Ncr值减小更为明显，进而UTR更易使FGM纳米梁达到热屈曲而失稳；同一升温类型下，边界约束较强，则频率、临界载荷及临界升温值均越大。其作用影响机理前文已有分析，这里不再赘述。

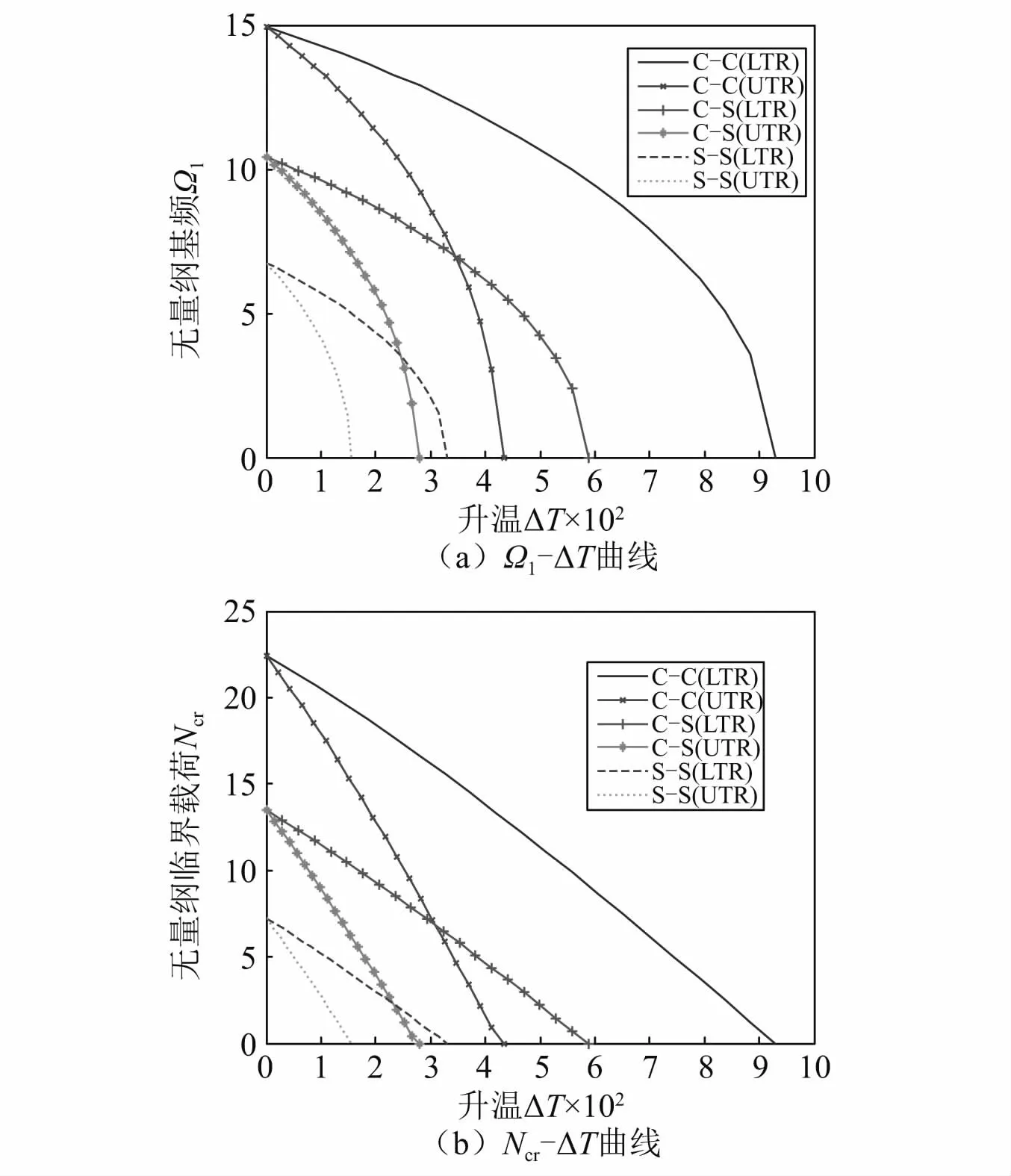
图5 FGM纳米梁的无量纲基频Ω1及无量纲临界屈曲载荷N cr随升温ΔT变化关系曲线Fig.5 Curves of dimensionless fundamental frequencyΩ1 and dimensionless critical buckling load N cr of FGM nanobeams versus temperature riseΔT

图6考虑了Np=-5，Np=-2，Np=0，Np=2，Np=5这5种取值，刻画了FGM纳米梁（p=1，μ=1，λ=20）在热-机耦合作用下FGM C-S纳米梁的Ω1-ΔT关系曲线:各Ω1曲线值都随线性升温ΔT的增加而单调减小，当ΔT=ΔTcr时，纳米梁发生热-机耦合屈曲而失稳。此外，取相同的ΔT值，由Np=2和Np=5对应的这2条基频曲线来看:初始轴向机械压力越大，则Ω1和ΔTcr值越小；由Np=-2和Np=-5对应的2条基频Ω1曲线来看:初始轴向机械拉力越大，则Ω1和ΔTcr值也越大。这是由于初始轴向机械拉力提高了纳米梁抗弯曲变形的能力。

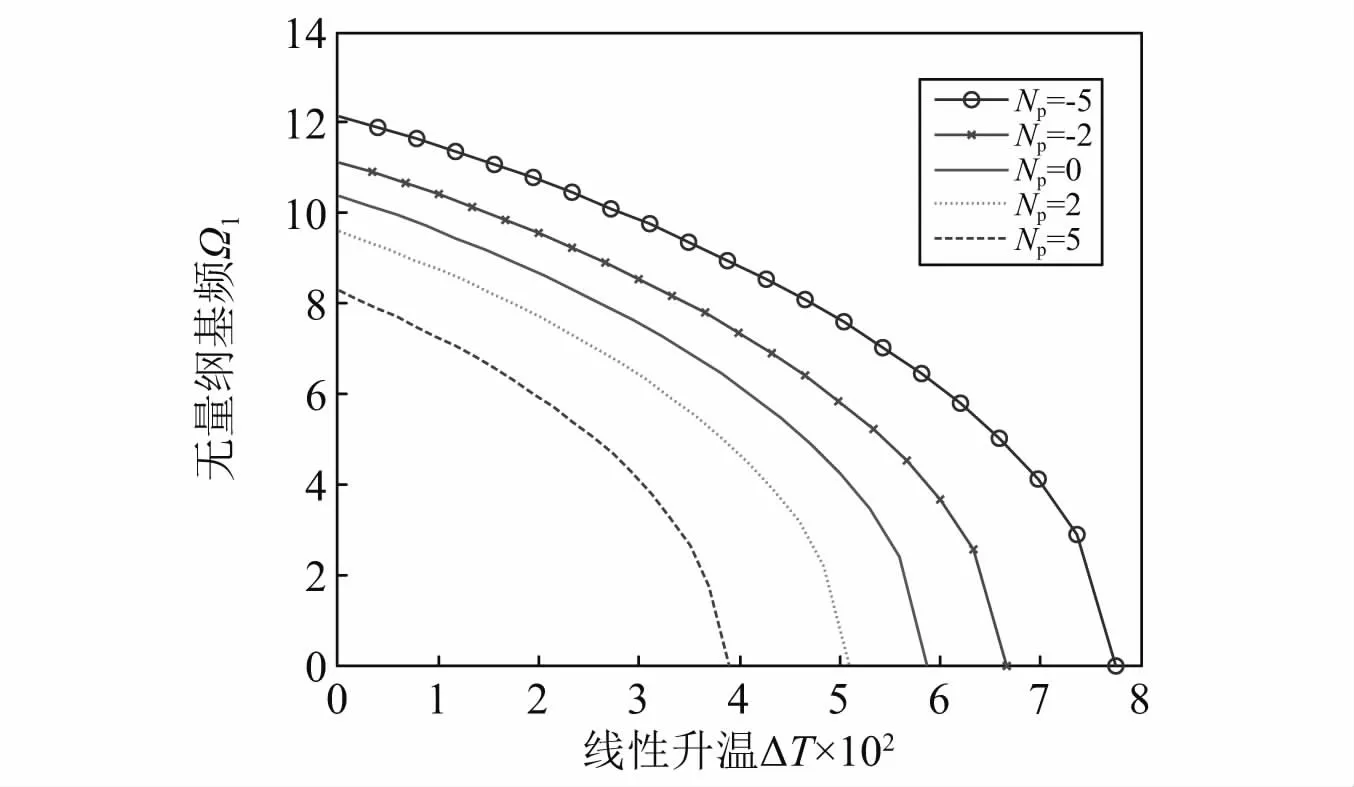
图6 C-S边界FGM纳米梁的无量纲基频Ω1随线性升温ΔT变化关系曲线Fig.6 Curves of dimensionless fundamental frequencyΩ1 of C-SFGM nanobeam versus linear temperature riseΔT

图7反映了NLTR升温ΔT=200 K及5种非局部参数μ=0，μ=1，μ=2，μ=3，μ=4取值时FGM纳米简支梁（p=1，Np=5）热-机耦合振动的Ω1-λ关系曲线:随着跨厚比λ的增大，各基频曲线Ω1值均先增大，随后单调减小，达到各自临界跨厚比λcr时，发生热-机耦合屈曲而失稳，此时Ω1=0。这是由于热载荷、机械载荷及跨厚比多因素共同作用引起的，此时FGM纳米梁的力学行为表现出复杂的耦合特性。此外，取相同的跨厚比λ，非局部参数μ值越大，基频Ω1越小，纳米梁达到热-机耦合屈曲时，λcr值也越小。即尺度效应越显著，频率和临界跨厚比越小，FGM纳米梁也更易失稳。

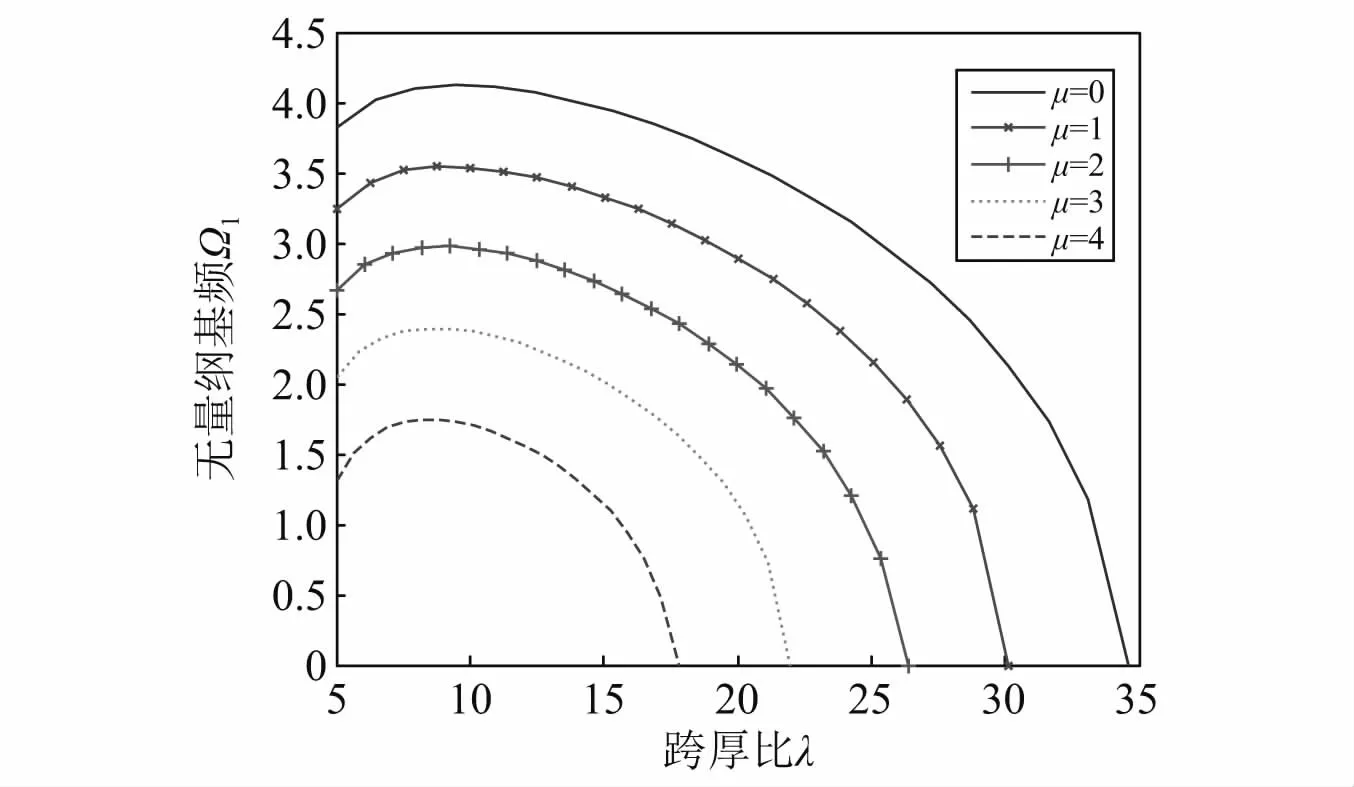
图7 FGM纳米简支梁热-机耦合振动的无量纲基频Ω1随跨厚比λ变化关系曲线Fig.7 Curves of dimensionless fundamental frequency Ω1 of S-SFGM nanobeam subjected to thermal-mechanical loads versus slenderness ratiosλ

图8反映了3种边界FGM纳米梁（μ=1，λ=20，Np=5，ΔT=100 K）热-机耦合振动的Ω1-p关系曲线:各基频曲线Ω1值先随材料组分梯度指标p的增加而显著减小，随后减小趋于缓慢。这是由于p增加的初始阶段，陶瓷成份Al2O3骤减，FGM纳米梁的整体刚度迅速降低而导致的。

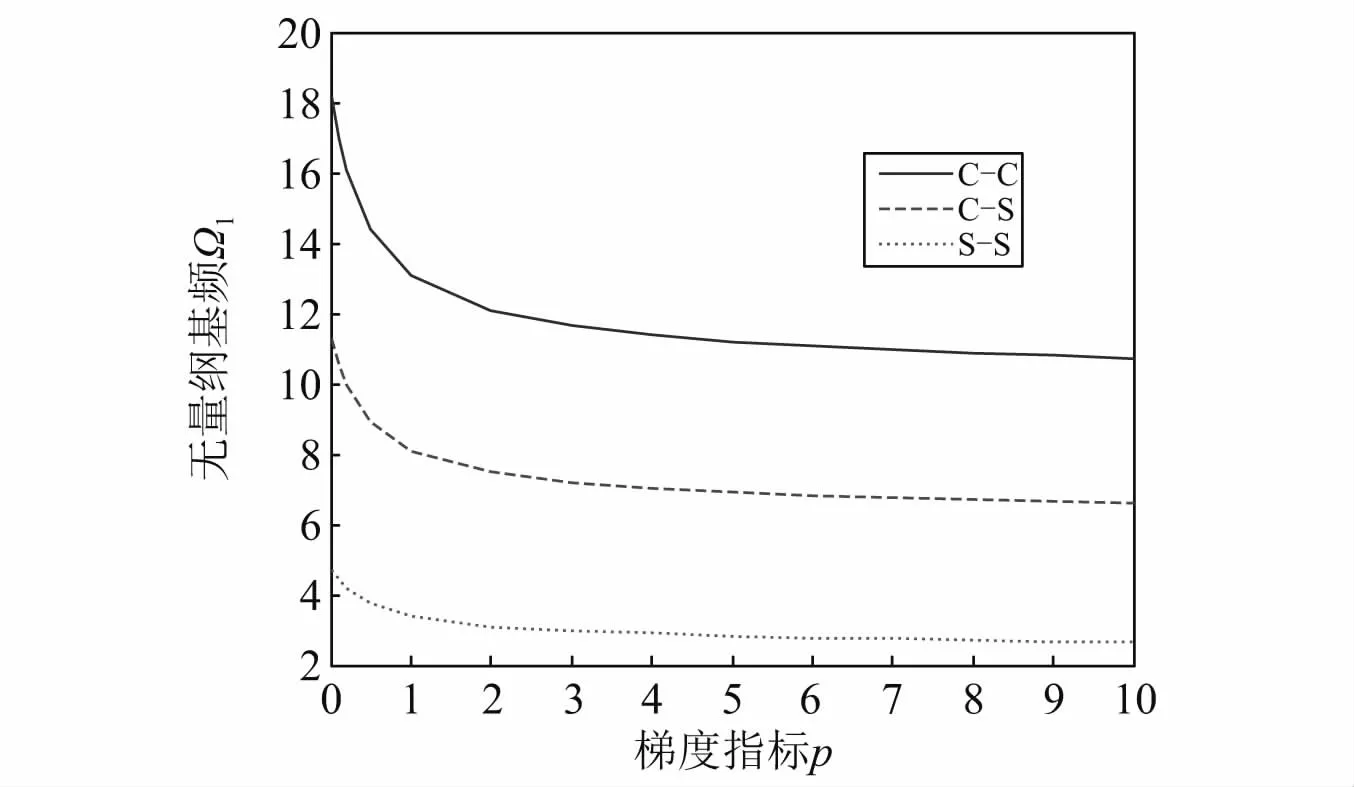
图8 热-机耦合作用下FGM纳米梁的无量纲基频Ω1随梯度指标p变化关系曲线Fig.8 Curves of dimensionless fundamentalΩ1 of FGM nanobeams subjected to thermal-mechanical loads versus material graded index p

4 结 论

通过引入边界条件控制参数，采用MGDQ法实施了3种边界FGM纳米梁动态响应求解的MATLAB统一化编程，初次优化了数值分析方法。基于静动态响应之间的二元耦联性实施解耦，通过循环子程序获得屈曲静态响应，二次优化了MGDQ法并提高了计算效率，为FGM微/纳结构的力学行为研究提供了一种切实可行、行之有效的分析方法。且研究结果表明:

（1）即使对于纳米尺度细长梁而言，随着阶次的增加，CBT仍明显高估纳米梁的高阶频率。而GBT具有重要的理论和工程应用价值，建议推广使用。

（2）FGM纳米梁的热-机耦合振动频率、临界载荷、临界升温值均随尺度效应非局部参数、轴向机械压力、升温、梯度指标的增加而减小。温度分布不同，其影响有显著差异。即UTR使FGM纳米梁频率减小最快，更易使梁失稳、LTR次之、NLTR则最为缓和。

（3）随着跨厚比的增加，FGM纳米梁热-机耦合振动的基频先增加，随后减小，达到临界跨厚比时发生热-机耦合屈曲而失稳，此时基频减小为零；微/纳尺度效应越明显，临界跨厚比则越小，FGM纳米梁此时更易失稳。