基于子模型收敛性评价的混合建模方法研究

白英君，张悦，田庆，罗代强

（1.华北电力大学控制与计算机工程学院，河北 保定 071000；2.华北电力大学河北省发电过程仿真与优化控制工程技术研究中心，河北 保定 071000；3.黔西中水发电有限公司，贵州 毕节 551700）

0 引言

根据机理模型与数据驱动模型的排列组合的顺序不同，混合模型基本形成了串联和并联两大结构，在并联型结构中，两种模型是可以互换顺序的，但是，串联型结构中则不然［1-2］。并联型结构是以机理模型为混合结构的核心，用于反映过程内部的动态行为，被控对象的复杂特性导致模型精度受到限制。数据驱动子模型预测机理模型与实际数据之间的残差［3］。该结构就是将两个子模型进行叠加，以提高混合模型整体的精度。Henricus J.L.van Ca［4］提出了并联型混合建模法，对混合模型与数据驱动模型从精度、外推能力等方面进行对比，说明了混合模型的优势。李景轩［2］运用机理与反向传播算法（Back Propagation，BP）神经网络并联混合建模方法建立了燃气机模型。姚源朝［5］采用机理与广义回归神经网络(General Regression Neural Network，GRNN)并联型混合模型建立了气流床气化炉模型。陈鸿伟［6］提出了一种结合机理建模和支持向量机的并联型混合模型用于蒸汽管道的参数计算方法。徐端［7］提出了多元线性回归和机理模型并联混合的炼钢连铸能耗模型。现在研究较多的以机理模型为主的串联结构，这种混合模型适用于底层的详细机制不确定，但是有海量的运行数据来推断出未知的参数。大数据集含有丰富的过程状态信息，虽然没有直接的物理解释，但是，可以利用数据驱动模型进行参数寻优，改善机理模型的预测精度。王广军［8］采用神经网络对难以确定的参数进行辨识，然后用于电厂锅炉的机理模型，实现了对锅炉系统的串联混合建模。罗雷涛等［9］以工业催化重整装置为研究对象，对脱氯前氢气纯度建立了最小二乘支持向量机与机理串联型混合模型。华丰等［10］采用人工神经网络（Artificial Neural Network，ANN）与机理模型串联型混合模型对工业乙烯裂解炉进行了建模。

混合模型只要对数据驱动部分进行足够的训练都能够有很好的模型精度。李景轩［3］等对各种结构对比得出，不同结构的混合模型精度相差不大，但都优于单一模型。因此，对于混合模型而言，单纯地从精度角度去评判其合理性有失公允，本文以数据驱动子模型权值搜索和收敛速度的角度为切入点，构建了一种新的结构，该结构反馈历史信息参与模型训练，与其他混合模型的对比，权值收敛速度优势更加明显。

1 并联型混合结构

目前研究最多的并联混合结构是图1（a）中的结构A，图1（b）中模型是结构A 的最常见的表现形式。应用最为广泛的串联结构是图1（c）中的结构B。图1（d）中的结构C在某些情况下等同于结构A［1］。

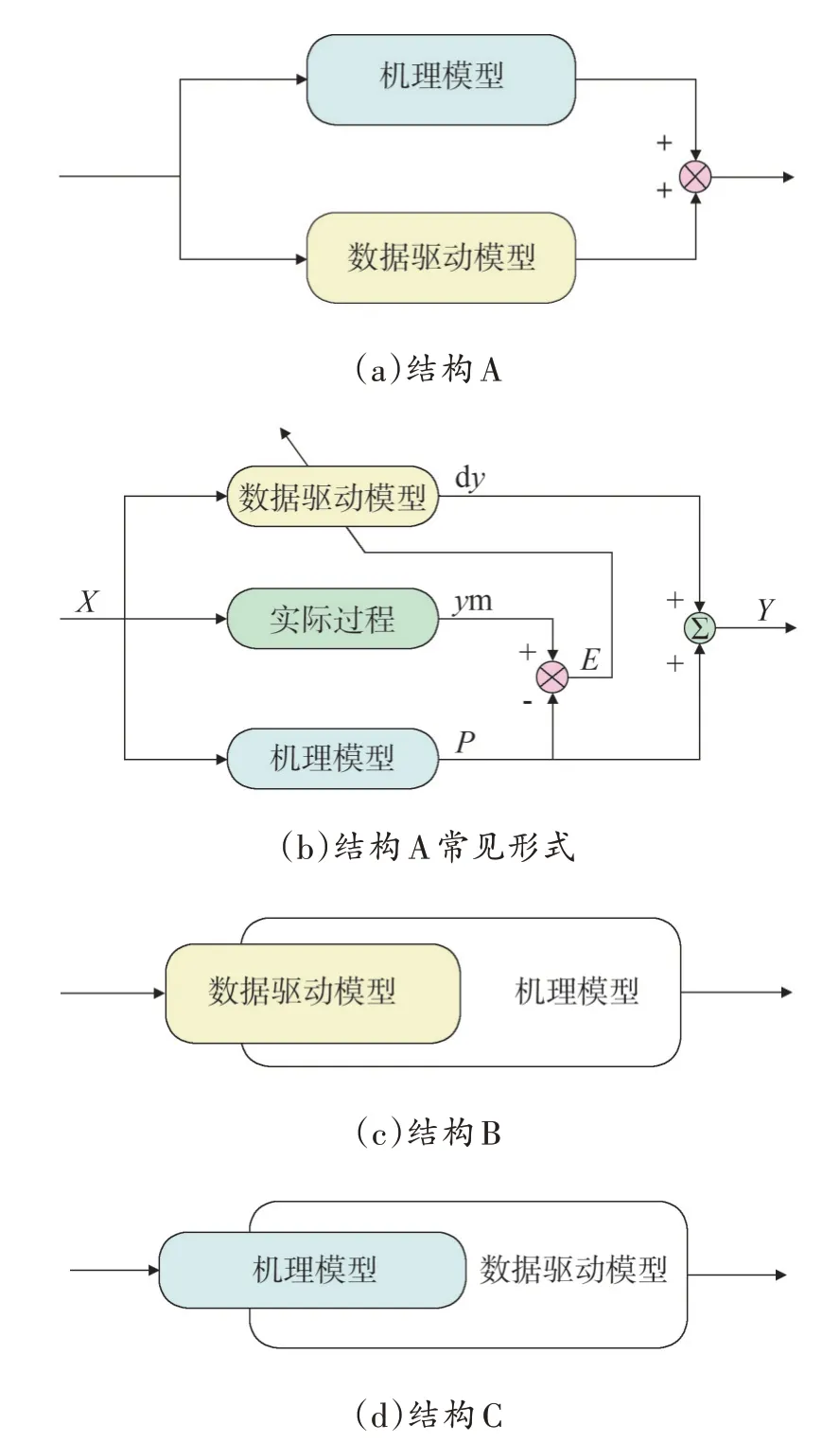
图1 串、并联型混合结构

数据驱动模型是由数据确定的，这种特点赋予了混合模型灵活性，可以从数据中挖掘出部分未知信息的影响。目前比较常见的数据驱动模型有支持向量机（Support Vector Machine,SVM）、多层感知机（Multilayer Perceptron，MLP）、BP 神经网络、径向基函数（Radial Basis Function，RBF）神经网络、深度神经网络等。

深度神经网络非线性拟合效果会更好，但是网络结构过于复杂，会把机理模型建立起来的可解释性全部覆盖，因此不适合本文的混合模型。SVM、MLP、BP、RBF 的预测效果都很不错，但是由于标准的训练方法不同，SVM、MLP 的训练时间比人工神经网络要长，同时，对于非线性的拟合能力也不如人工神经网络。BP 神经网络的结构要比RBF 神经网络简单得多，同时，BP 有一个致命的缺陷，就是容易陷入局部极小值，RBF 神经网络则不然，理论上，RBF神经网络可以实现以任意精度的逼近任意的非线性函数，且具有全局的逼近能力［11-12］，从根本上解决了BP 神经网络的局部最优问题，而且拓扑结构紧凑，收敛速度快，泛化能力好。RBF神经网络结构如图2所示。

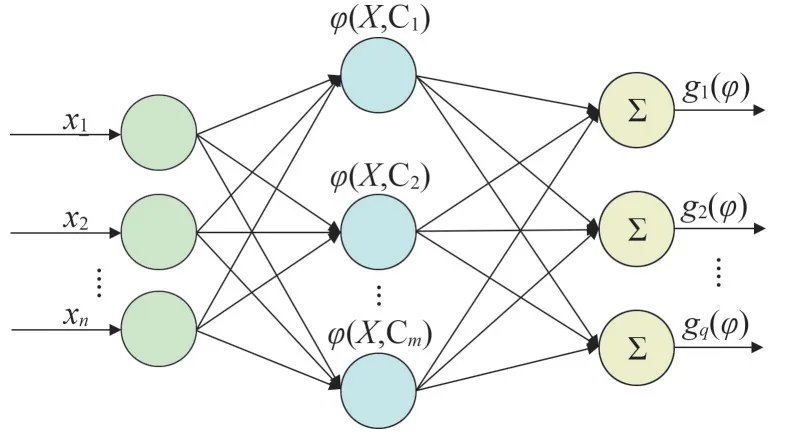
图2 RBF神经网络

建立如图3 所示的新的并联结构D。把机理模型的预测结果与RBF 神经网络的预测进行线性组合，最终得到混合模型的预测结果。该结构在训练时神经网络的权值与线性组合的系数同时进行调整。

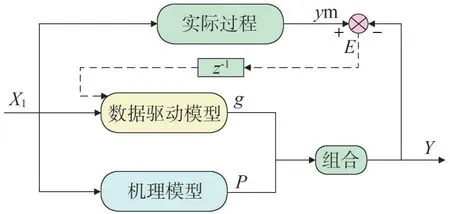
图3 并联型结构D

结构D 和结构A 在结构方面最大的区别在于对混合模型中的数据驱动部分的处理，结构A中数据驱动模型相当于时间序列滑动平均模型的预测，误差的预测只和过程对象输入信号有关。滑动平均模型为

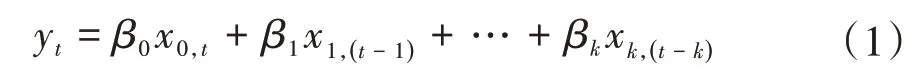
式中：yt是模型输出；xi，t为第i个变量t时刻的模型输入；βi是系数。

结构D 中模型相当于自回归滑动平均模型，误差的预测不仅仅和过程对象输入信号有关，还和输出自身的历史信息有关系。所以在D 结构里面，误差的预测会被限制在一个相对小的范围。自回归滑动平均模型为

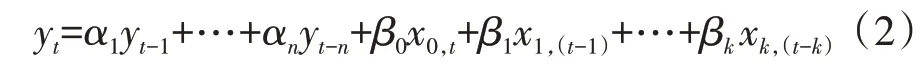
式中：yt-i是前i个时刻的输出；αi是系数。

2 混合模型的构建

2.1 机理模型的构建

凝汽器压力是模型预测的目标。凝汽器压力的大小受型式、型号、总有效面积、抽真空区有效面积、传热系数、循环水流量、清洁系数等技术参数的影响，其中最主要的因素是汽轮机排入凝汽器的蒸汽量、冷却水的进口温度和冷却水流量。

建模假定如下：采用集总参数法，认为凝汽器壳侧各处的压力相同。1）进入凝汽器的蒸汽全部为饱和蒸汽，且全部冷凝成水；2）忽略管中水的蓄热导致的传热的延迟。

在如上假设基础上可以近似认为，凝汽器凝结成水时释放出的热量、通过冷却管的传热量、冷却水带走的热量三者是相等的，于是，蒸汽侧在稳定工况下热平衡方程为

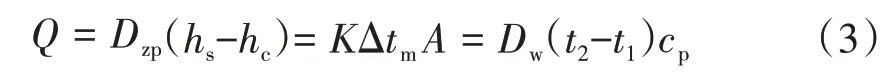
式中：Q为凝汽器热负荷；Dzp为汽轮机排汽进入凝汽器的蒸汽流量；hs为汽轮机排汽的焓；hc为凝结水的焓；K为总传热系数；Δtm为对数平均温差；A为冷却面积；Dw为进入凝汽器的冷却水流量；t2为冷却水出口温度；t1为冷却水入口温度；cp为冷却水比定压热容，cp=4.181 6×103J（∕kg·℃）。

hs可以根据变工况下抽汽的热力参数值来确定，hc可通过查饱和水对应的温度下的焓值或根据经验公式得到。但通过此方法确定汽轮机低压缸排汽焓计算复杂，且其本身存在一定的误差，所以在实际工程计算中，当凝汽式汽轮机在正常的压力内运行时，hs与hc之间的差值变化很小，通常直接取

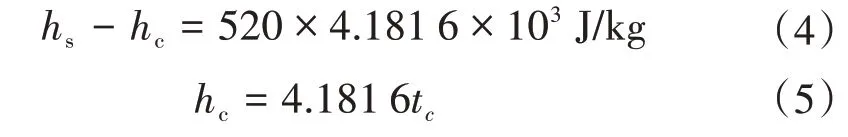
式中：tc为凝结水的饱和温度。

由式（1）可得温升为

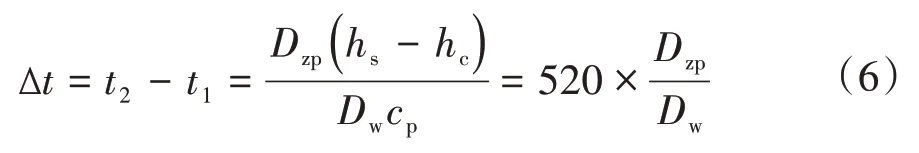
设δt=ts-t2，δt为传热端差，ts为排汽压力对应的饱和蒸汽温度，可知

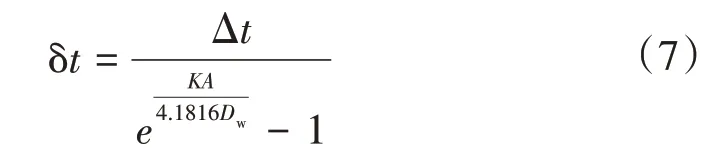
凝汽器压力对应的饱和蒸汽温度

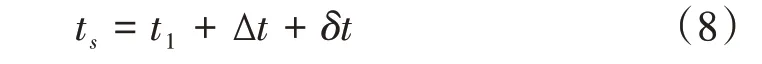
式（3）、式（6）、式（7）代入上式可得

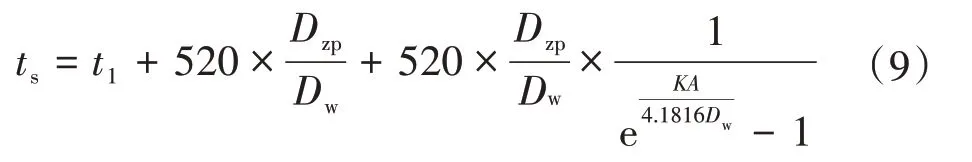
冷却面积A结合实际凝汽器设计参数与其运行规程，此处给出经验值。

总传热系数K可以通过美国传热学会公式进行求解。

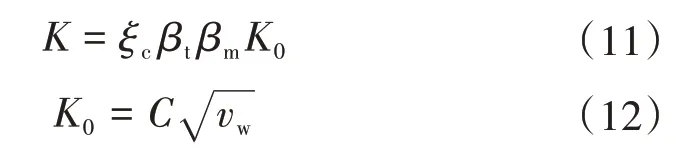
式中：K0为基本传热系数，可以通过式（10）求得；ξc为清洁系数；βt为冷却水入口温度修正系数；βm为冷却管材料和壁厚的修正系数；vw为冷却管内流速；C为取决于冷却管外径的计算系数。

采用Bunk 公式［13］将饱和蒸汽温度转化为对应的凝汽器压力，当t＞0℃时

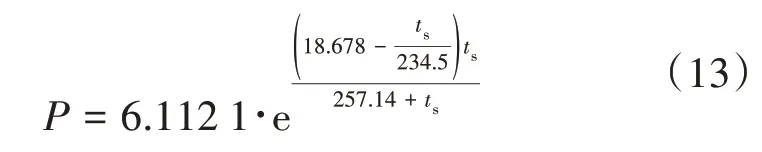
根据建立的机理模型，可得预测值与实际值之间的误差，如图4所示。

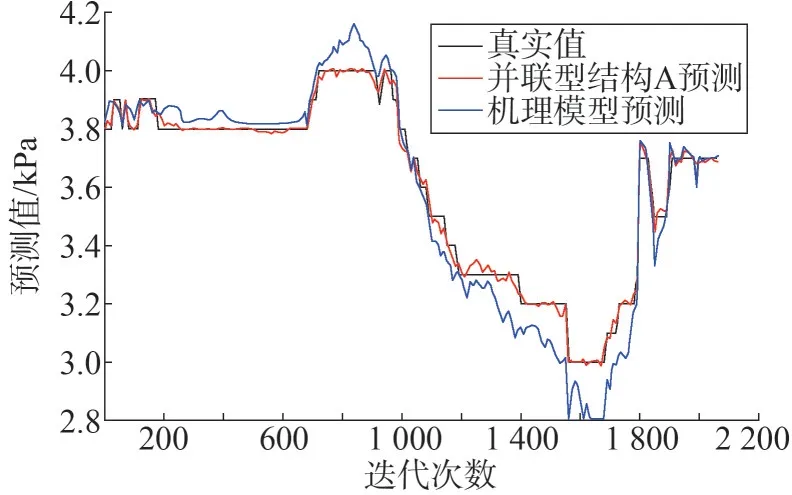
图4 机理模型预测

从图4 可以看出，机理模型预测的凝汽器压力与实际压力在趋势上保持了一致，但是在某些工况下预测不是十分准确。这主要是由于采用了集总参数法进行建模，在建模过程中作了较多的假设、简化和经验公式。这也从另一方面说明了建立凝汽器模型采用机理和数据驱动相结合的方式的必要性。

2.2 数据驱动模型的构建

为了能够表述一些机理不明或者极其复杂不可描述的因素对凝汽器实际压力的影响，结构D 采用了RBF 神经网络对凝汽器压力进行了数据驱动建模，根据2.1 中机理建模可知，影响凝汽器压力的因素有很多，其中最主要的因素是汽轮机排入凝汽器的蒸汽量、冷却水的进口温度和冷却水流量。因此，选择上述3 个变量为数据驱动模型的输入变量，凝汽器压力为输出变量。结构D 取前3 个时刻的历史值反馈到RBF 的输入，因此该结构采用了六输入单隐层单输出的网络结构。

RBF 神经网络隐含层神经元个数的选择可以根据过程数据中包含的工况个数来决定。RBF 隐含层神经元的中心点的选取，可以通过聚类来实现，把聚类中心作为核函数的中心点。

训练结构D 中RBF 神经网络时，首先需要对过程数据进行滤波，然后把汽轮机排入凝汽器的蒸汽量、冷却水的进口温度和冷却水流量以及误差的历史值作为输入量提供给RBF 神经网络。然后，RBF的输出与机理的输出线性组合得到结构D 的预测值。最后，结构D 的预测值与实际值之间的误差来修正RBF 的权值与线性组合系数。同时，当前误差作为一个历史值反馈到RBF 输入，参与到下一次权值修正。

2.3 混合模型的构建

结构D 中两个模型的组合采用的是最简单的线性组合，建立步骤如下。

高斯核函数可表示为

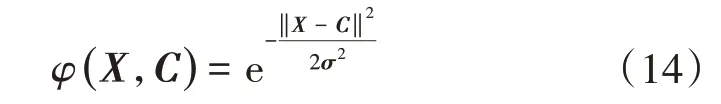
式中：X是神经网络输入向量，包含输入X1和前3 时刻E的反馈；C是核函数的中心；σ是核函数的宽度。

采用的线性组合为

式中：g为数据驱动模型的预测值；设机理模型为P=f(X)，P为机理模型预测值。据结构D 可知，该模型整体输出表示为

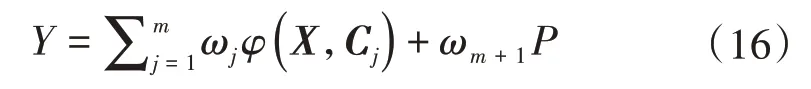
式中：Y为混合模型预测值；j为第j个隐含层神经元；m为隐含层神经元个数；ωj为第j个隐含层神经元的权值。

损失函数为

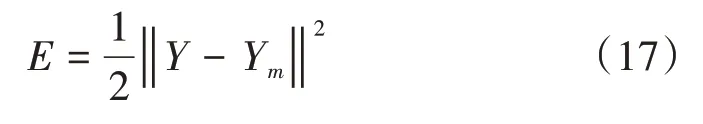
式中E均方误差，Ym是实际数据。

设e=Y-Ym，网络权值更新为

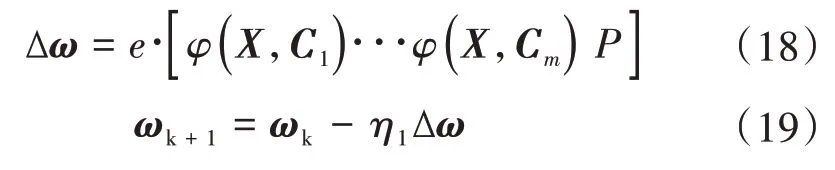
隐含层神经元中心点更新：

隐含层神经元高斯核宽度更新：

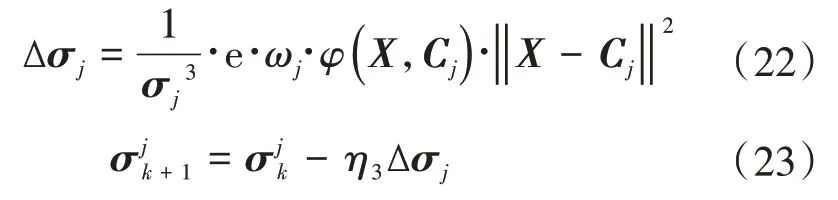
式中：k为迭代次数；η1、η2、η3分别是权值、核函数中心点、核函数宽度的学习率。

3 仿真

以某1 000 MW 火电机组凝汽器压力为例，并联型结构A、结构D 和机理模型进行了对比实验，最后从数据驱动子模型权值搜索空间及收敛性的角度进行了仿真实验。

3.1 混合模型仿真

结构A 数据驱动网络结构和输入变量同结构D，不同的是结构A网络输出为实际数据与机理的残差。因此，并联结构A 是以机理模型为主，机理模型的预测值与基于残差的RBF 神经网络输出叠加，得到混合模型输出，仿真效果如图5、图6所示。

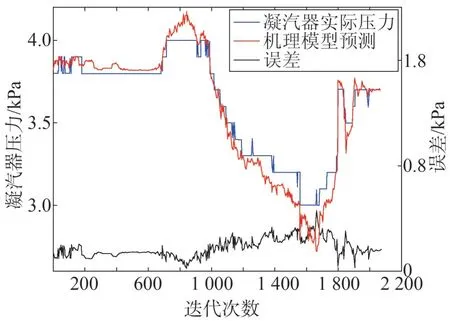
图5 并联型结构A与机理预测对比

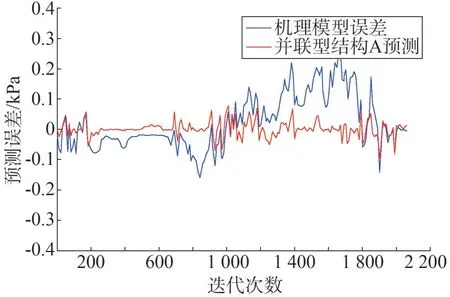
图6 并联型结构A与机理误差对比

并联结构D 是在数据驱动子模型中引入了机理模型的预测以及结构D 输出的误差历史信息，混合模型的整体输出是机理子模型预测与数据驱动子模型预测的加权和。仿真效果如图7、图8所示。

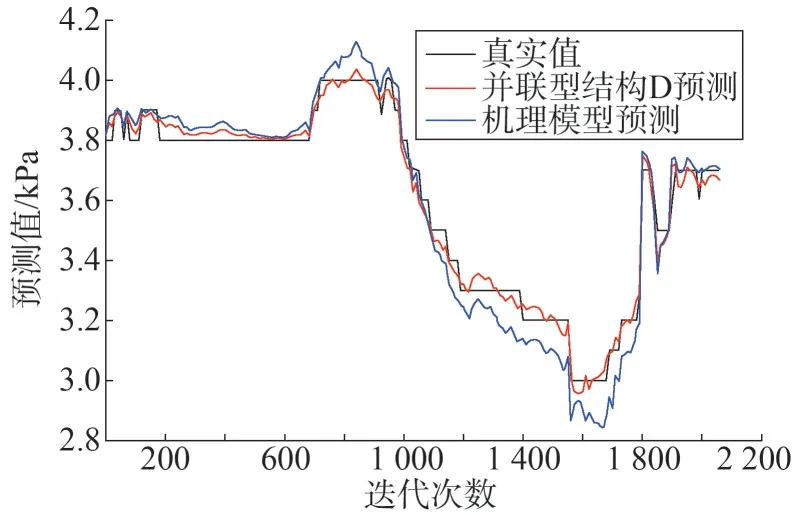
图7 并联型结构D与机理预测对比

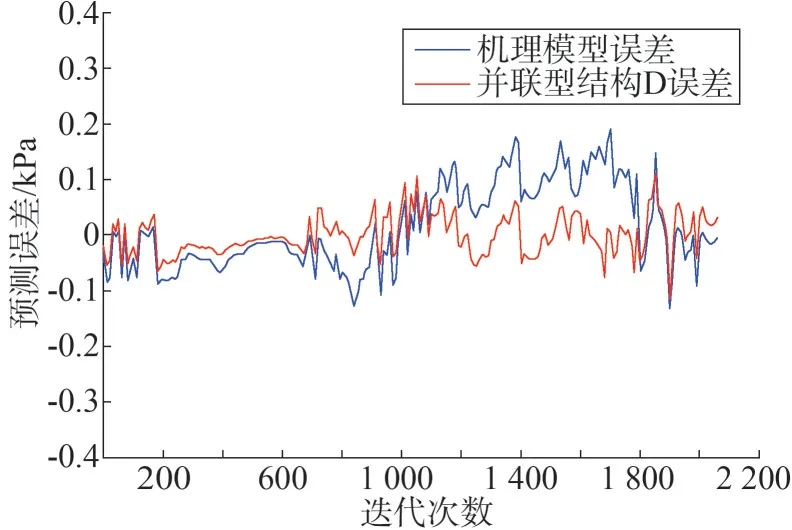
图8 并联型结构D与机理误差对比

据图4、图5、图7 可知，并联型结构A 与结构D的预测效果都优于单一的机理模型。混合模型在机理模型预测基础上做了补偿和修正，使得混合模型能够更加真实的反映系统内部的运行机制。表1 从均方误差的角度证明了，混合模型有较高的精度，但是相差不大。根据建模对象的不同，不同结构会有不同的精度表现，所以单纯从精度角度评判混合模型结构没有找到问题的核心。

表1 机理与混合结构预测误差对比

3.2 子模型收敛性评价

结构A 和结构D 中数据驱动部分网络结构和神经元个数会影响模型的收敛性和准确性。六输入单隐层单输出的网络结构已经确定，本文中隐含层神经元数量是根据工况决定的，通过观察功率和凝汽器压力的数据，大致可以确定数据中包含的工况为7～10 个。经过大量试算和比较，确定隐含层神经元个数为8。

从数据驱动子模型权值搜索空间及收敛性的角度，设计了如下仿真实验，并联型结构A 与结构D 的RBF 神经网络权值搜索空间如图9、图10 所示，收敛速度如图11所示。

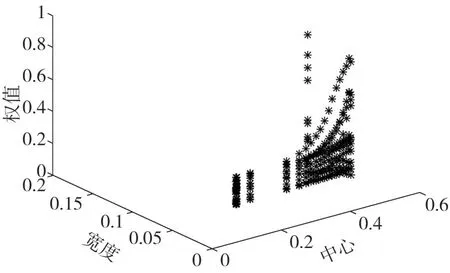
图9 并联型结构D权值搜索空间

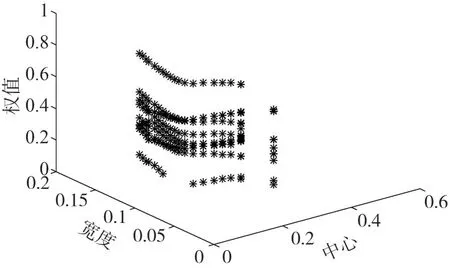
图10 并联型结构A权值搜索空间

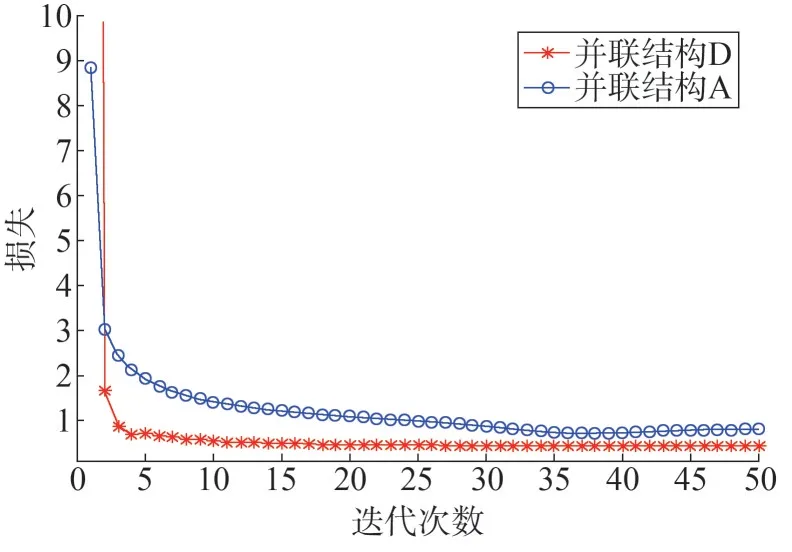
图11 并联结构损失函数对比

据图9、图10、图11 可知，结构D 的RBF 神经网络权值搜索空间比并联型结构A 要小，权值收敛速度更快。并联结构A 数据驱动部分在训练残差网络时与机理的输出是无关的，两者互不影响，因此，RBF 神经网络权值搜索范围大，收敛慢。结构D 的数据驱动部分虽然训练的也是残差，但是通过与机理模型输出加权求和，对机理模型进行了校正，同时在数据驱动模型部分引入了自回归信息，这就保证了结构D 的精度不弱于结构A。除此之外，据式（14）可知，结构D 中机理模型的输出通过加权系数ωm+1影响RBF神经网络的训练。当机理模型的输出与实际值已经比较接近的情况下，其加权组合的系数ωm+1会是一个接近于1 的较大数，同时该结构反馈的历史信息限制了RBF 神经网络的权值搜索空间，使得该结构的权值搜索范围小，更容易获取到最优值，收敛速度快。

4 结语

采用基于子模型收敛性评价的并联型混合建模方法，以某1 000 MW 火电机组为例，建立了凝汽器的机理模型，然后在RBF 神经网络中引入机理模型的预测，得到并联型结构D 的整体输出。通过对比机理模型、并联型结构A 和建立的并联型结构D，可以看出，混合模型的精度优于单一的机理模型。但是，不同结构的混合模型精度相差无几，单纯从精度角度评判混合模型结构有失公允。从数据驱动子模型权值搜索空间和收敛速度进行评判，通过仿真得出，并联型结构D 中历史信息的反馈和机理模型的存在约束了数据驱动子模型的权值搜索空间，提高了搜索效率，收敛速度更快。因此，仿真使用并联型结构D构建精准度高、收敛速度快的模型是可行的。