基于贝叶斯优化的线性自分段神经网络在阀门流量辨识中的应用

路 宽，王文宽，孟祥荣，李 军，杨子江，张森烨

（1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.山东科技大学电气与自动化工程学院，山东 青岛 266590；3.国网山东省电力公司烟台供电公司，山东 烟台 264000）

0 引言

火电机组在运行的过程中形成了海量高维数据，集中储存在厂级监控信息系统（Supervisory Information System，SIS）和分布式控制系统（Distributed Control System，DCS）中，这为汽轮机阀门流量特性曲线辨识工作提供了丰富的基础数据。汽轮机阀门流量特性的准确辨识以及调节参数的优化能够有效提升火电机组一次调频品质和自动发电控 制（Automatic Generation Control，AGC）协调水平［1］。传统上，汽轮机阀门流量特性是通过现场试验人员对目标机组进行解列后手动测试计算得到的。同时，不同工况下的阀门流量特性受主蒸汽压力、主蒸汽流量、机组各阀后压力等多个因素的影响。因此，在大数据背景下，反映这些因素的测点数据质量会反过来影响阀门指令与阀门流量之间的关系［2-5］。

黄彦浩等［6］提供了在电力系统仿真领域开发大数据技术的基本框架。盛锴等［7］为了实现汽轮机阀门流量特性问题的全过程管控，基于大数据运行环境开发了一套汽轮机阀门流量特性在线监测优化系统，该系统可实现对阀门流量特性的在线监测和阀门流量函数的滚动优化。朱彦等［8］针对火电机组的热力系统存在复杂、高维、非线性、时变性、参数冗余性等导致的传统建模方法无法准确反映机组运行特性问题，采用聚类分析、多项式拟合的方法对168 万组运行数据进行了调门特性辨识，并基于流量特性线性化考虑，优化了汽轮机数字电液调节系统（Digital Electronic Hydraulic Control，DEH）阀门管理函数，提升了机组变负荷能力和一次调频能力。李存文等［9］基于多种经典数据挖掘算法的对比分析，合理改进了K-medoids 算法，提出了一种用于汽轮机流量特性分析的多元线性回归方法，有效解决了机组出现的线性度不合理问题。尚兴宇等［10-11］利用流量校正的方法对阀门开度进行优化，并使用反向传播（Back Propagation，BP）神经网络对优化后的阀门流量特性进行了模拟还原。邹包产等［12］在流量特性数据处理过程中应用了神经网络，并使用最小二乘法确定了最佳的汽轮机汽门流量曲线调节量；试验结果表明，校正后的汽轮机调阀流量曲线具有良好的线性度，从而可提高机组网源协调能力。王志杰等［13］通过对机组的历史运行数据进行筛选，提出了一种基于最小二乘支持向量机（Least Squares Support Vector Machines，LSSVM）的汽轮机阀门流量特性辨识方法。

虽然上述研究均给出了阀门流量曲线的辨识方法，但主要辨识模型往往采用了非线性函数。在实际优化阀门函数的过程中，给定流量下得到最优阀门指令值的过程实际是一个求解辨识模型反函数的过程。如果辨识的非线性函数不存在反函数，那么就无法实现阀门函数的精准修正。利用前馈神经网络（Forward Neural Network，FNN）实现了对阀门流量特性数据的分段线性辨识，同时使用了贝叶斯优化的方法得到了最优分段数，这就保证了阀门流量特性的辨识函数具有反函数，从而在给定阀门流量时能够提供唯一的阀门指令解。最后，所提方法在山东省某火电机组上进行了应用与辨识，得到了验证。

1 阀门流量特性的优化

阀门流量的优化主要包括阀门特性辨识和阀门调节参数优化两个部分。

在辨识过程中，火电机组汽轮机蒸汽流量获取通常有直接测量、给水流量法、凝结水流量法以及间接计算等方法［8］。文献［14］中基于弗留格尔公式演变的流量计算公式被主要应用在基于大数据场景下的阀门流量特性识别中，如式（1）所示。

式中：Q为等效实际流量，%；pi为调节级压力，MPa；p0为主蒸汽压力，MPa；pie为额定工况下的调节级压力；p0e为额定工况下主蒸汽压力。辨识的结果则形成了阀门总指令μ与实际进汽流量Q之间的阀门流量曲线函数：

在阀门调节参数优化过程中，令PCV=f（μ）表示原始阀门管理函数，PCV为单个阀门阀位指令［7］，Q*=g*（μ）表示表示理想阀门流量特性曲线，那么，优化后的阀门管理函数可以表示为：

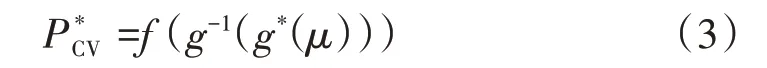
显然式（3）的有解需要阀门流量曲线函数g存在反函数。

2 基于贝叶斯优化的线性自分段神经网络

2.1 FNN分段线性拟合网络

由于流量曲线拟合是后续阀门优化工作的先决条件，而机器学习中非线性拟合得到的输入——输出函数是无法计算反函数的，这就无法为阀门函数的优化提供可操作的建议。把FNN作为阀门流量曲线函数g（·）的具体形式，同时通过在FNN 中引入ReLU 激活函数使其变成线性分段函数，那么就可以确保g-1（·）的存在［15］。

人工神经网络（简称神经网络），是一种模仿生物神经网络的结构和功能的数学模型或计算模型，其通过梯度下降法不断更新每层网络中的神经元，从而具备了学习能力，一般用于对函数进行估计或近似。前馈神经网络，是神经网络中最常见的一种。它采用一种单向多层结构，其中每一层包含若干个神经元。在此种神经网络中，各神经元可以接收前一层神经元的信号，并产生输出到下一层，如图1所示。

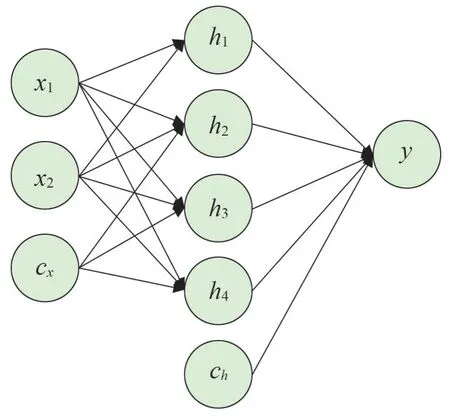
图1 前馈神经网络

FNN中的多层前馈神经网络是一个单输入、输出层和多中间层的前馈网络结构。它每一层都有多个神经元，图2给出了FNN中单个神经元的详细结构。

图2 神经元结构

图中，xi和yi分别是神经元的输入、输出，wi是对应每个输入的权重，f（·）表示激活函数；θ是截距参数。这里，选取ReLU［16］作为FNN的激活函数，即为

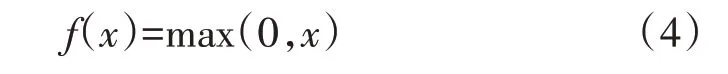
ReLU 函数由于具有稀疏性结构，使得神经网络在输出的过程中并不激活所有的神经元。相比于Sigmoid 激活函数和tanh 激活函数，ReLU 激活函数由于没有上下界，因此在训练过程中不会存在神经元饱和的情况；同时，由于对ReLU 函数求导为常数，因此训练过程中也不存在梯度消失的问题，这就为加深神经网络深度创造了条件。

通过在模型输出层的上一层神经元先进行ReLU 激活后再逐项相加，就可以得到自动分段的线性拟合函数。令倒数第二层神经元个数为n，那么拟合的分段函数段数为n+1。

如图3所示，最后一层网络的数学表达式为

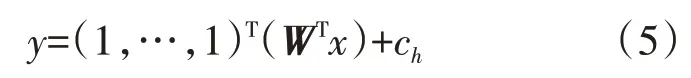
式中：x为网络中倒数第二层中间层的输出值，在图3中就是（h1，h2，h3，h4），这些变量均通过了ReLU 函数进行激活；WT是倒数第二层网络与最后一层连接的权重向量；ch是常数值；为了使最后一层网络的输出达到分段线性表达的效果，倒数第二层的输出值要进行直接相加，因此需要用（1，…，1）T与（h1，h2，h3，h4）进行向量乘法，这里（1，…，1）T的维度是1×4，其中：4是一个超参数，可以在建模时任意选取。

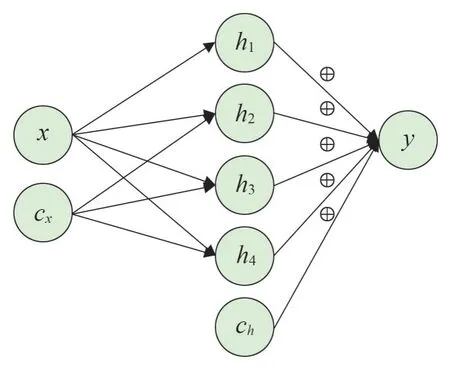
图3 分段线性函数的神经网络结构

2.2 最优线性分段数求解

FNN 分段线性辨识模型能够对阀门流量进行分段线性辨识，但线性分段数目作为模型的超参数需要人为设定。为了能够自动完成线性分段数量的确定，使用贝叶斯优化方法。

2.2.1 高斯过程回归

高斯过程（Gaussian Process，GP）是概率论和数理统计中随机过程的一种，是一系列服从正态分布的随机变量在一指数集内的组合［17］。

高斯过程回归（Gaussian Process Regression，GPR）［18］假定输入向量与目标输出之间的关系f为高斯过程，则f～GP(m，K)。其中：m表示过程f的均值向量，K表示协方差矩阵。对于训练集D={(Xi，yi)|i=1，2..，n}，其中Xi和yi分别表示第i个输入和目标输出，向量表示为X和y。构建回归模型为

式中：ε为噪音，服从正态分布，ε～N(0，σ2)，σ2表示噪声的标准差向量。

对于输入向量X，假设f（xi）服从高斯分布，则f（X）服从多元高斯分布

f（X）～N（m（X），K（X，X））

通常均值向量设为0，那么有

f（X）+ε～N（0，K+σ2）

当出现新的输入变量向量X*时，由于假设f（X*）服从高斯过程，满足

f（X*）～N（0，K*）

那么训练集和新输入向量的联合分布也满足高斯过程

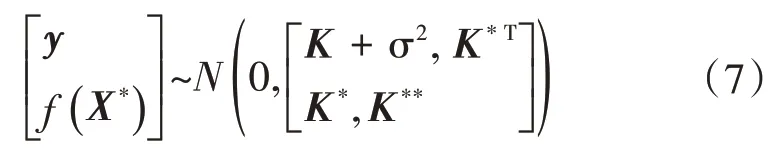
式中：K*=k（X，X*），K**=k（X*，X*），k（·）表示协方差函数，也称为核函数。变换式（7）得到的f（X*）的后验概率分布也满足高斯过程

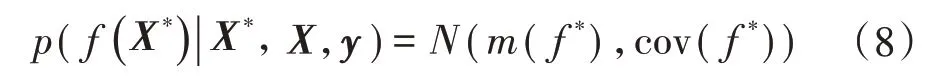
其中，m(f*)和cov(f*)的具体形式如下：

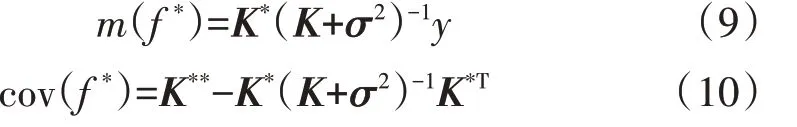
2.2.2 基于贝叶斯的线性分段数寻优

贝叶斯优化（Bayesian Optimization，BO）是基于数据使用贝叶斯定理估计目标函数的后验分布，然后再根据分布选择下一个采样的超参数组合。它充分利用了前一个采样点的信息，其优化的工作方式是通过对目标函数形状的学习，并找到使结果向全局最大提升的参数［19］。目标函数和采集函数（Acquisition Function，AC）［20］构成了BO 的两个重要组成部分。这里的目标函数采用了GPR，采集函数选取了置信下限（Lower Confidence Bound，LCB）函数，表达式为

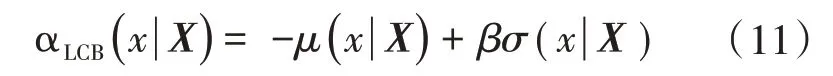
式中：μ（x）=m（f*），σ（x）=cov（f*）；X是已经观测到的点集，x是未知的候选点，相当于式（7）中的X*；β是人为设定的超参数。

2.3 算法整体流程框架

综合BO 应用于FNN 的训练过程以确定最优线分段数，主要包括神经网络训练和超参数的贝叶斯优化寻优两个阶段。

步骤1：设定线性分段数的超参数，对FNN 分段线性网络进行训练，观测验证集误差的变化情况。

步骤2：使用BO 对步骤1 中设置的线性分段数进行寻优，重复步骤1 的过程直到验证集误差触发阈值。这里，通过设定验证集的均方根残差（Root Mean Square Error，RMSE）作为停止步骤1、2的阈值，图4给出了整个过程的流程展示。

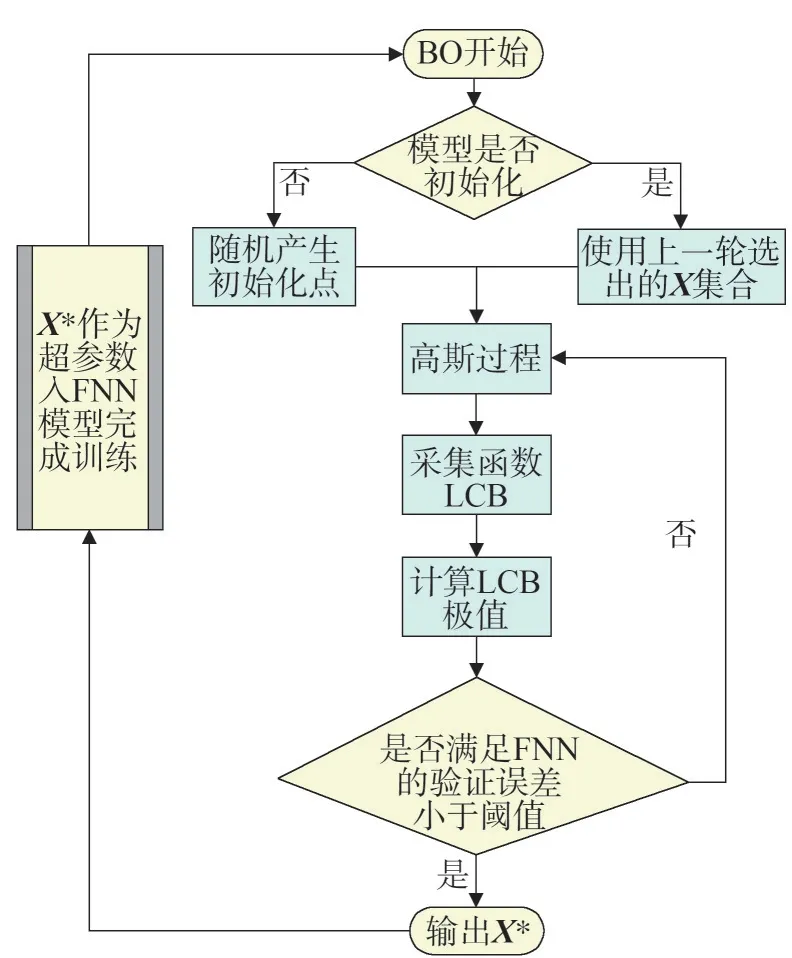
图4 基于BO的FNN线性分段数寻优框架

3 实际应用

选取山东省某电厂330 MW机组作为应用对象，特征参数选取了有功功率、主汽流量、主控指令、调节级压力信号。所有数据的时间长度为6 个月，时间周期为5 s，共计315万组。

3.1 数据预处理

由于数据量较大，为减少阀门流量特性辨识过程中的误差，针对海量机组运行数据进行了数据预处理，主要包括以下3个方面：

1）剔除异常值。使用了箱型图法完成对异常数据的识别与剔除。

2）机组运行方式筛选。由于在提取数据的时间周期内，机组存在单阀和顺序阀交替运行的情况，为了排除不同运行方式对特性辨识效果的影响，从剔除异常值后的数据中单独提取了单阀运行方式下的数据。

3）等效流量计算。根据主汽压力与调节级压力的关系，使用式（1）计算出了不同调节级压力下的等效流量。

数据预处理后的主要特征参数如表1所示。

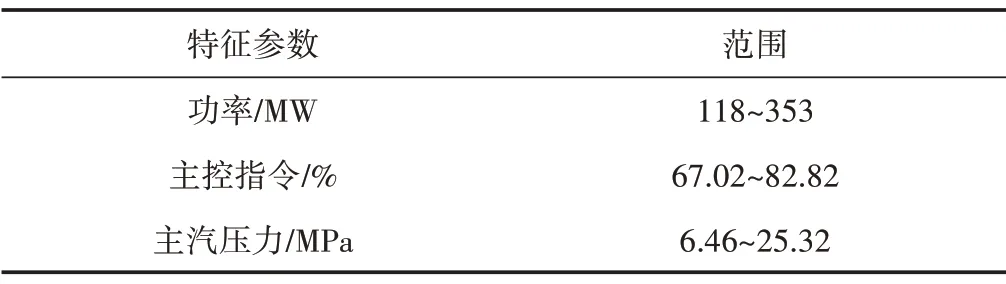
表1 模型主要参数

3.2 阀门流量特性辨识

按照70%和30%的比例划分训练集和验证集，验证集用来对BO 的优化效果进行验证。这里的FNN 模型选取了4 个隐藏层的全连接前馈神经网络，每个隐藏层的神经元数量分别为128、256、256和32；同时，将线性段数的超参数范围设置为［1，20］，其表明该网络可以给出的潜在线性分段数区间。

在BO优化的过程中，选择了GPR作为FNN误差函数的近似，采集函数函数选择了LCB 函数。同时，使用了限制内存的拟牛顿算法（Limited Memory Broyden Fletcher Goldfarb-Shanno，L-BFGS）求解AC函数的最优解。此外，为了提高FNN训练的速度，在Pytorch 建模的基础上使用了图形处理器（Graphics Processing Unit，GPU）进行训练加速，并将Batch_size设置为128，最后使用了自适应矩估计（Adaptive Moment Estimation，ADAM）进行参数优化。

通过BO 寻优，本次应用案例数据的最优的线性分段数为4，此时对应的验证集误差为0.004 56，图6给出了模型的辨识结果，可知该模型能够对汽轮机阀门流量特性实现较准确地辨识。

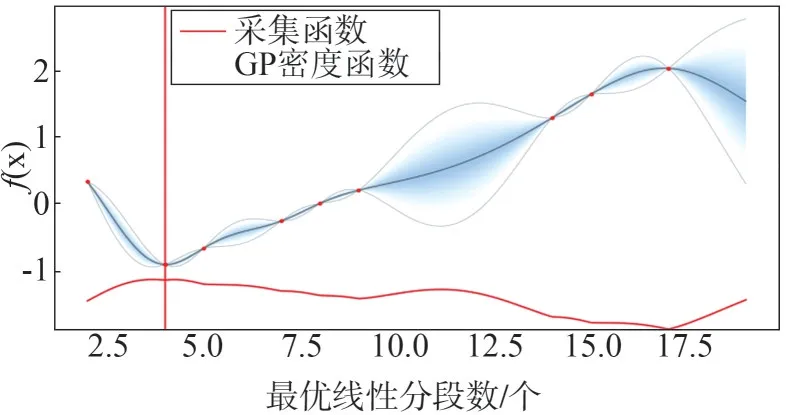
图5 线性分段数BO寻优

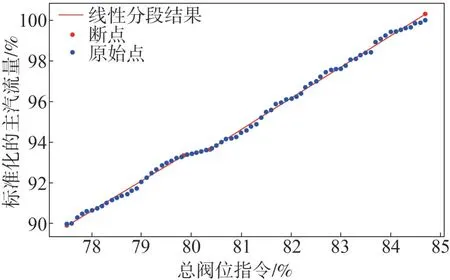
图6 基于BO的FNN线性自分段模型辨识

4 结语

通过将ReLU 激活函数引入FNN 网络实现了阀门流量特性的分段线性可辨识，同时在FNN 的训练过程中引入BO 方法实现了对线性分段数进行自动寻优。所得到的线性分段函数可以较好地实现对阀门流量特性的辨识，同时满足了辨识函数存在反函数的要求，进而为阀门控制函数的精准优化提供了可靠的基础。