空载合闸励磁涌流对变压器绕组受力的影响

王继豪，曹志伟，孙福春，辜 超，商攀峰

（1.山东电力研究院，山东 济南 250003；2.国网山东省电力公司电力科学研究院，山东 济南 250003）

0 引言

早在1892 年，人们就发现变压器进行空载合闸操作时可能出现励磁涌流［1］。励磁涌流中含有明显的直流分量和谐波分量，会降低电能质量，提高功率损耗，还可能引起变压器保护误动和谐振过电压［2］。目前，学者们主要采用波形对称原理、小波分析方法、二次谐波制动方法、神经网络方法、模糊辨识等方法辨别励磁涌流以避免差动保护误动［3-9］，但难以消除励磁涌流的不利影响。

据统计，国内外已有多台变压器在空载合闸时出现乙炔含量异常升高或发生匝间短路故障，例如：天生桥一级水电站主变压器在倒送电期间多次投切，变压器投运后出现乙炔，且每次投切后乙炔含量均会出现不同程度的增加［10］；国内某水电厂主变压器在高压侧进行空载合闸时，变压器出现励磁涌流，约2.5个周期后出现匝间短路故障，随后发展为接地短路故障，变压器起火爆炸；国外也曾发生多起变压器空载合闸过程中烧毁的案例。这些变压器故障时均伴随较大的励磁涌流，说明变压器故障与励磁涌流有一定的关联性。

国外部分学者怀疑励磁涌流可能是引起变压器故障的潜在因素之一，并提出从绕组受力的角度开展研究。文献［11］研究了50 MVA 单相变压器在励磁涌流作用下的受力，研究表明励磁绕组端部位置径向漏磁通和轴向力增长明显，会损坏端部支撑结构件，导致绕组变形。文献［12］基于2D 有限元模型研究了励磁涌流对三相变压器的影响，发现当励磁涌流只有短路电流的60%时，绕组局部受到的轴向力将与短路时的受力相当，绕组整体受到的轴向力甚至是短路时的3 倍。考虑到励磁涌流可持续数秒或几十秒，文献［13］基于变压器2D 有限元模型进一步研究了绕组受力的时变性，研究发现若励磁涌流与短路电流相同，即使在合闸操作2.4 s后，励磁涌流产生的轴向力依然大于短路电流产生的轴向力。当出现短路电流时，现场往往通过绕组变形试验等方式及时判断绕组是否变形［14］。出现励磁涌流时，现场往往不做检测，无法评估励磁涌流的破坏作用，对励磁涌流电磁力作用认识不够深入。

励磁涌流会导致铁芯饱和，绕组间磁势不平衡，漏磁通不再局限于绕组之间，采用简化的2D 模型难以准确反映变压器饱和后的磁通分布［10］。同时，文献大都针对双绕组变压器，而大型电力变压器往往具有多层绕组，需要具体情况具体分析。为此，建立自耦变压器3D 有限元模型，对比研究励磁涌流和短路电流作用下高压绕组受力情况。

1 变压器建模

1.1 变压器参数

研究的国产单相壳式变压器型号为DSP-260000，采用日本高日铁30ZH110 硅钢片，冷却方式为强迫导向油浸式水冷，各参数如表1所示。

表1 变压器参数

由于变压器容量较大，该类变压器多采用自耦变压器，采用多层层式绕组结构，具有两个高压绕组和两个低压绕组，并按照“高压绕组I—低压绕组I—低压绕组II—高压绕组II”的结构排列，如图1所示。

图1 变压器绕组

1.2 变压器有限元模型

变压器的正常工作是基于电磁感应原理，为了研究变压器在短路故障、铁芯饱和情况下的运行状态，需要研究其内部磁通密度分布规律。目前，广泛采用的研究方法是有限元分析法。根据有限元建模复杂程度的不同，又可以分为2D 有限元模型和3D有限元模型。通常，分析变压器正常运行及外部短路故障时的磁通密度分布规律，2D 有限元模型已经具有足够的精度。3D 有限元模型一般用于分析不规则磁场和对精度要求较高的场合。

考虑到变压器出现励磁涌流后，铁芯饱和，变压器不同于正常运行状态，简化后的2D 有限元模型能否准确仿真该运行工况存在疑问。为此，同时建立变压器2D 和3D 有限元仿真模型，对比研究两种模型的准确性，如图2所示。

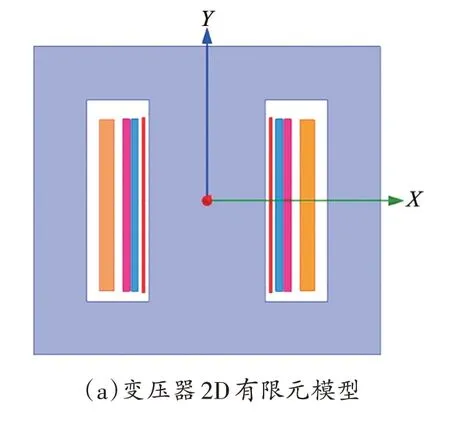
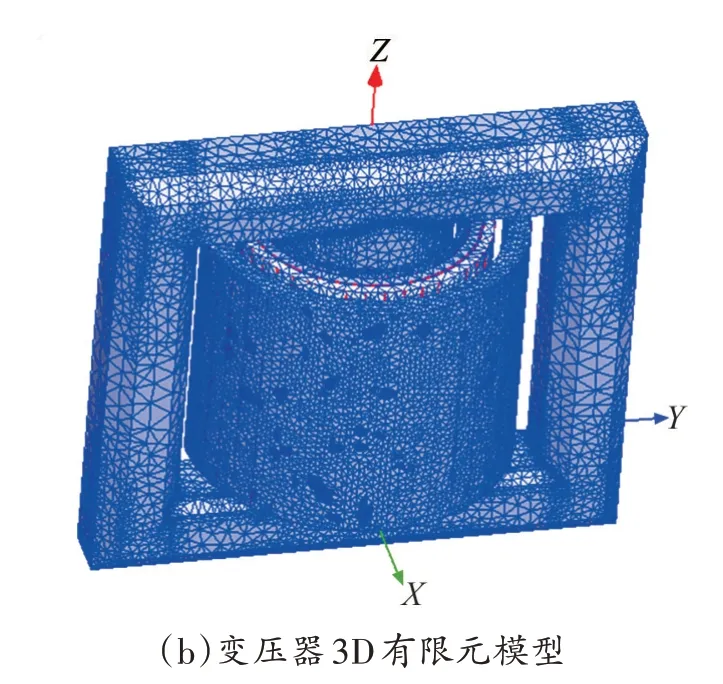
图2 变压器有限元模型

分别令变压器低压侧发生短路、高压绕组出现3 pu 的励磁涌流，利用上述两个模型计算绕组中磁感应强度分布，研究发现：当短路时，两个仿真模型结果一致；当出现励磁涌流时，两个仿真模型结果差别较大。

由图2（a）可知，变压器2D 有限元仿真模型默认铁芯和绕组沿垂直纸面方向无线延伸，即绕组始终被铁芯包围，这与实际情况不同［15-16］。实际变压器结构如图2（b）所示，只有左右旁轭和上下铁轭包围绕组。当变压器流过短路电流时，高低压绕组间磁动势平衡，铁芯是主磁通的主要流通路径，高低压绕组之间是漏磁通的主要流通路径［17-18］。此时，虽然绕组大部分并未被旁轭和铁轭包围，但变压器铁芯没有饱和，空气中的漏磁通很小。采用2D 模型简化计算是可行的，两种仿真模型计算结果相同。当变压器出现励磁涌流时，高低压绕组间磁动势不平衡，铁芯因磁通密度过高而饱和，漏磁通不再局限在高低压绕组之间。此时，两种仿真模型计算结果差异较大，2D 有限元模型无法准确计算铁芯饱和后的磁通密度分布。为了提高仿真结果的准确性，采用变压器3D有限元模型。

2 变压器绕组受力理论计算

当变压器短路或出现励磁涌流时，变压器内部磁通密度分布可以通过3D 有限元仿真模型计算出来。若知道绕组中流过的电流，就可以计算绕组受力，进而分析绕组变形机理［19-20］。

2.1 短路电流计算

假设电源电压为u=Umsin（ωt+α），则变压器低压侧短路时电路方程为

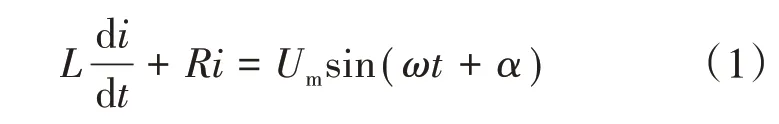
式中：i为短路电流；Um为电压峰值；ω为角频率；α为初始相位角；L为漏电感；R为电阻。

式（1）是一阶微分方程，最终解可分为稳态分量和暂态分量。计算可得，短路电流的最终表达式为

当α=0 时，即在端电压经过零点时发生突然短路，短路电流的瞬时值在ωt=π时达到最大值，即

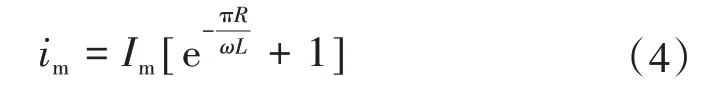
经计算，变压器最大短路电流可达额定电流的18.43倍（15 080 A）。

2.2 变压器受力计算

变压器绕组由相互绝缘的单根或多根导线并联绕制的多个线段组成，线段间用相应耐热等级的绝缘垫块隔开。为了减少并联导线间的环流损耗，并联绕组连接处需进行换位。绕组的实际结构较复杂，为简化问题，可认为导线之间紧密结合，可将绕组看作一个整体，电流在绕组横截面上均匀分布，如图3所示。

考虑到绕组厚度一般可达十几厘米，虽然不同部位的电流密度是相同的，但不同部位的磁通密度有所差异，例如：对于图3 中的绕组，靠近铁芯部位的磁通密度较小，随着径向距离的增大，磁通密度呈线性增长。为便于数值计算，可以将绕组划分为N×M个单元（径向划分为N等份、轴向划分为M等份）。

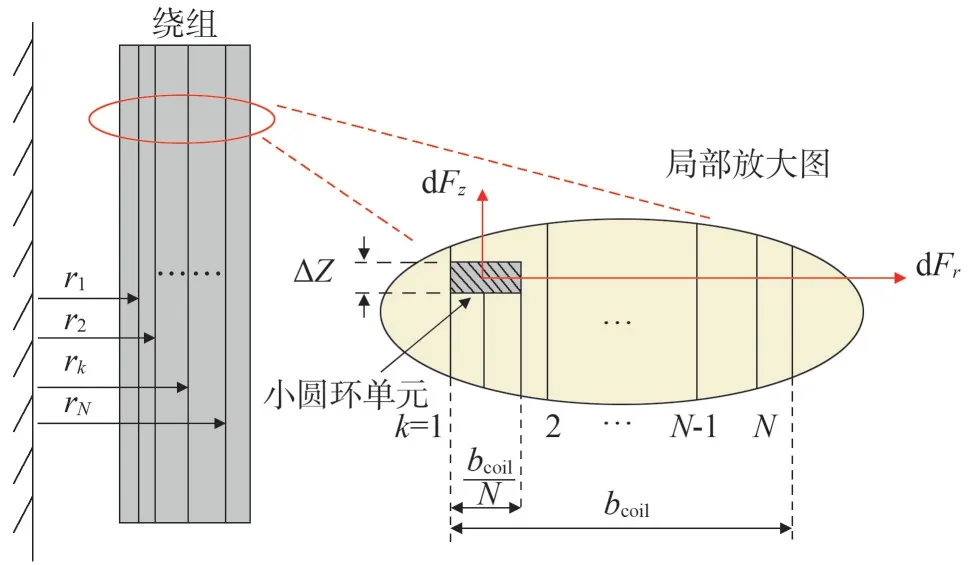
图3 变压器高压绕组分割

只要绕组分割数量足够多，每个单元内的磁通密度B就可以认为是相同的；可以认为绕组上的电流均匀分布，则电流密度J就等于总电流与绕组横截面积的比值。

在三维柱坐标系中分析变压器绕组受力，由于绕组沿着圆周方向缠绕，则只有圆周方向上有电流流过，轴向电流密度Jz和径向电流密度Jr为0，即

式中：Jφ为电流密度在圆周方向上的分量。

每个分割单元上的局部电磁力面密度为

每个分割单元同时受到径向力（r轴）和轴向力（z轴），计算如式（8）—式（9）所示。

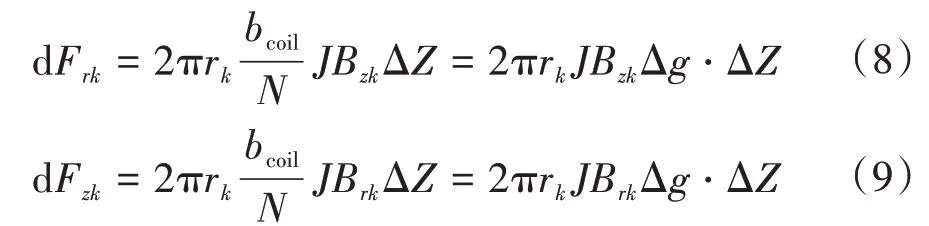
式中：Bzk为第k个分割单元处磁感应强度B的z轴分量，k=1，2，…，N；Brk为第k个分割单元处磁感应强度B的r轴分量；bcoil为绕组宽度；rk为第k个分割单元半径；Δg为分割单元的厚度；ΔZ为分割单元高度。

半径为rk的分割单元有M个，将这M个分割单元受到的轴向力叠加就可以得到半径为rk、厚度为Δg的一薄层绕组整体受到的轴向力，即

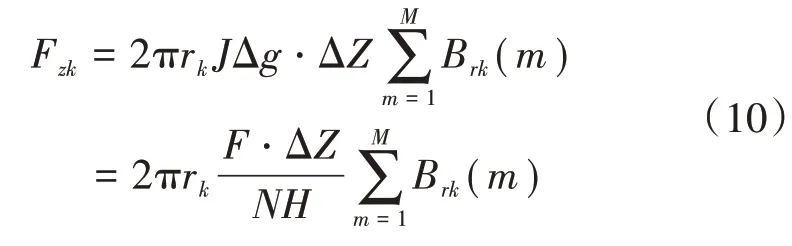
式中：F为磁动势；H为绕组高度。

式（10）得出一薄层绕组受到的轴向力，将N个这样的薄层受到的轴向力叠加就是整个绕组受到的轴向力，即

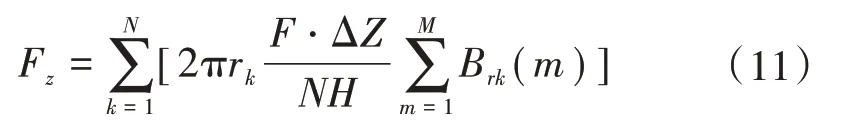
径向力将导致绕组沿径向整体扩大，绕组横截面上将受到拉力，若拉力足够大可能导致绕组断裂。绕组横截面受力如图4所示。

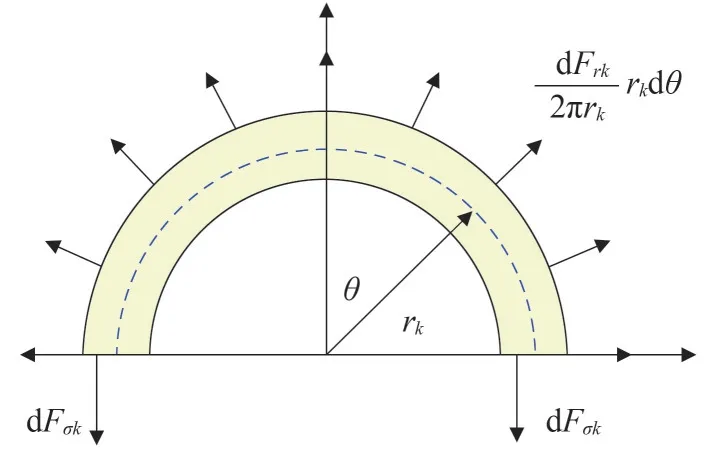
图4 高压绕组横截面受力分布

半径为rk的分割单元受到的拉力为

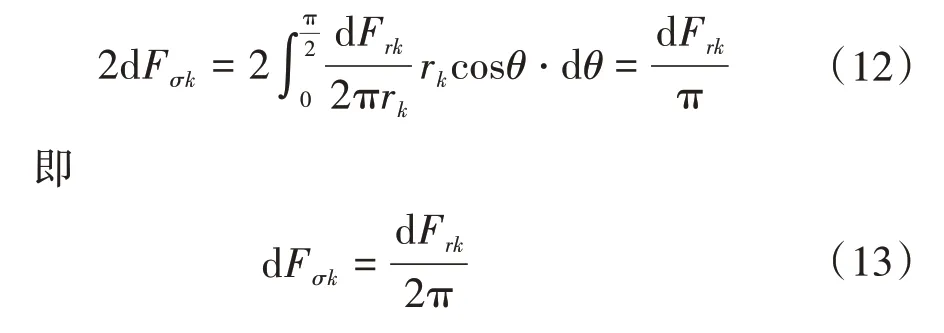
绕组横截面上整体受到的拉力为

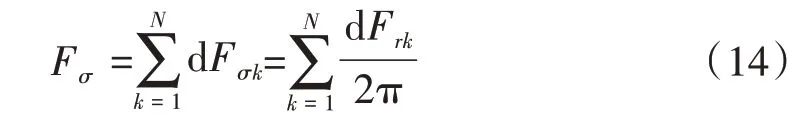
绕组横截面上的应力为

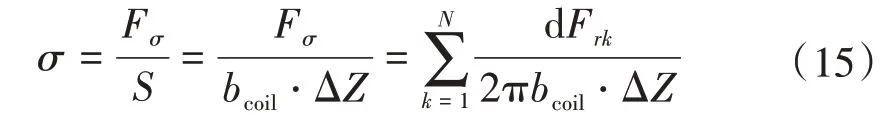
式中：σ为应力；S为绕组横截面积。

3 变压器内部磁通密度分布

基于变压器3D 有限元模型，研究励磁涌流和短路电流（fault）作用下变压器内部磁通密度分布情况。为定性说明问题，假设变压器高压绕组出现1 pu、3 pu、7 pu、11 pu 的励磁涌流，取图1 中高压绕组I 和II 中间部位进行分析。两部分的磁感应强度的轴向分量Bz和径向分量Br分别如图5和图6所示。

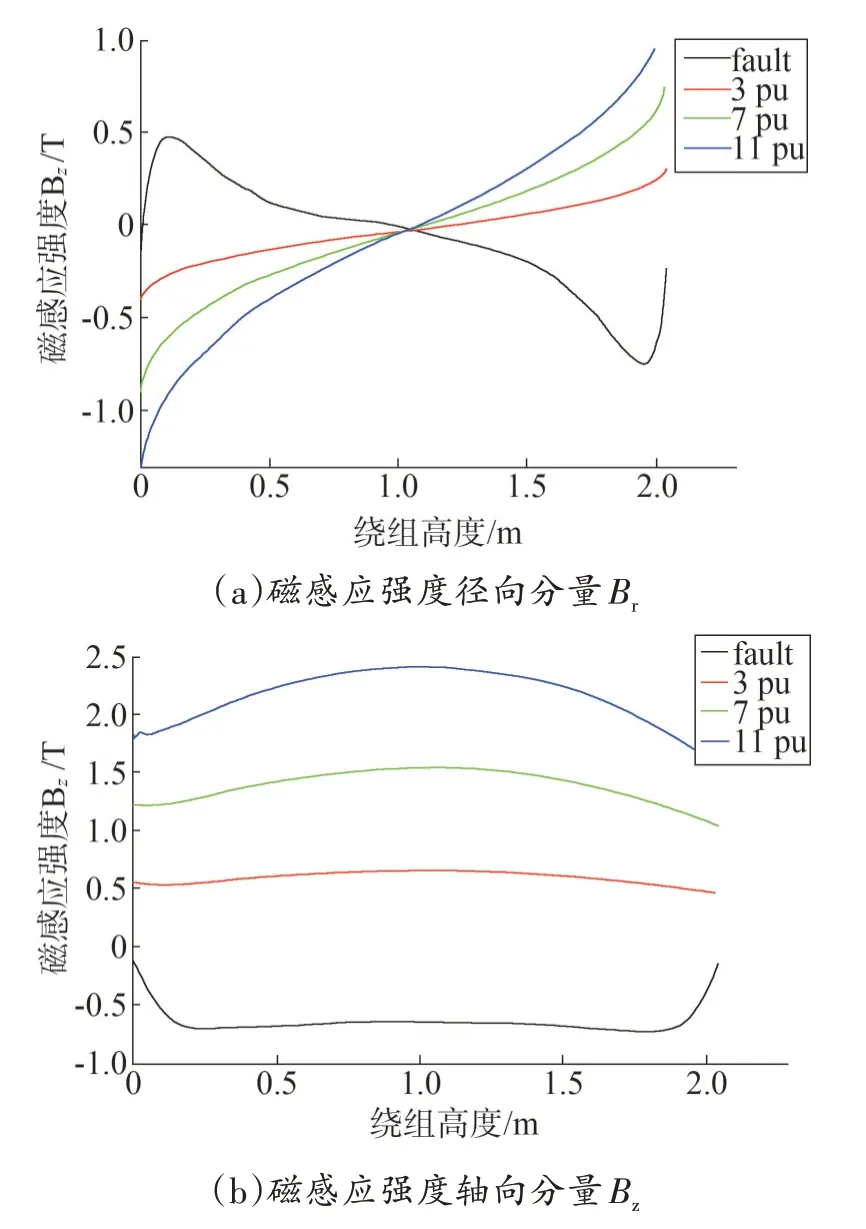
图5 高压绕组I磁感应强度分布

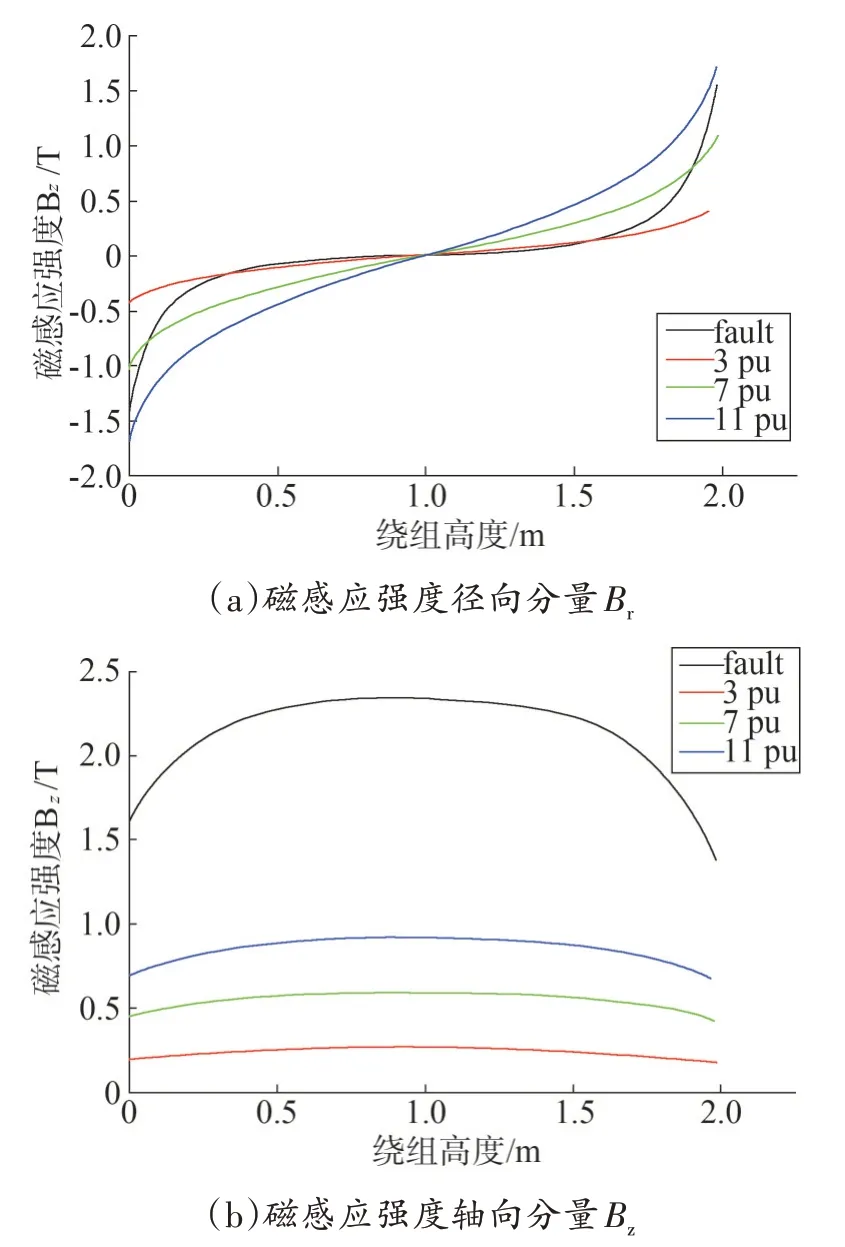
图6 高压绕组II磁感应强度分布

对比图5和图6可知，短路时，高压绕组I距离端部1∕5 处Br和Bz最大；高压绕组II 端部位置Br最大，中间位置Bz最大。

出现励磁涌流时，高压绕组I端部位置Br和Bz最大。Br和Bz的方向与短路时不同。高压绕组II 端部位置Br最大，中间位置Bz最大。相对于短路，较小的励磁涌流就可以产生较大的Br和Bz。

为了直观展示变压器内部磁感应强度分布规律，可以绘制磁感应强度矢量分布图。以变压器高压绕组出现7 pu 的励磁涌流为例，比较在短路和励磁涌流作用下，变压器内部磁感应强度的矢量分布情况，如图7和图8所示。

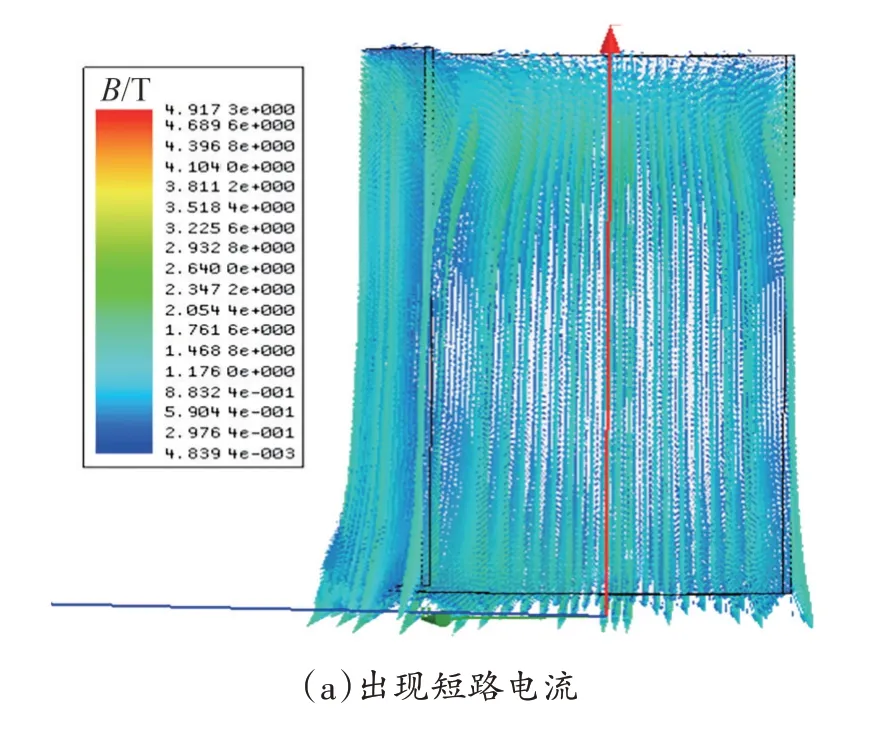
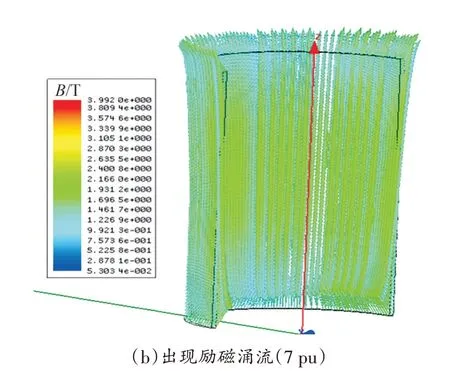
图7 高压绕组I中的磁感应强度分布

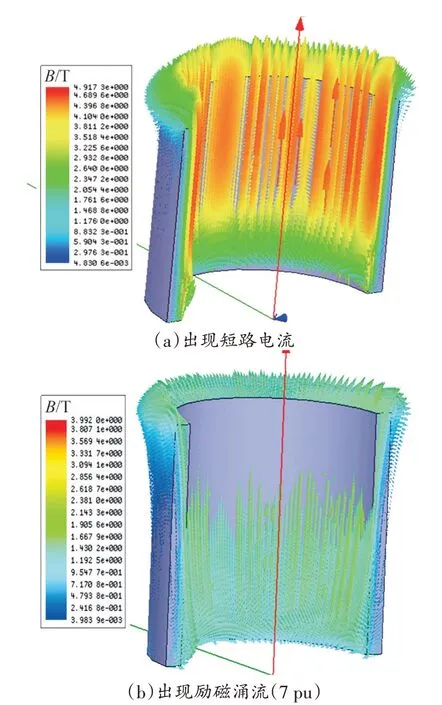
图8 高压绕组II中的磁感应强度分布

对比图7 和图8 可知，相对于短路故障工况，出现励磁涌流时，高压绕组I中磁感应强度的方向发生明显变化，而高压绕组II 磁感应强度方向未发生明显变化。分析结果于图5、图6一致。

4 变压器绕组受力仿真分析

当出现励涌涌流时，磁感应强度大小和方向发生变化，绕组受到的轴向力和径向力也将随之发生改变。绕组受力改变可能引起绝缘垫块错位、绕组变形等问题，进而诱发变压器故障。为此，需要从绕组受力的角度评估励磁涌流的影响。

为定性说明问题，令变压器在高压侧空载合闸，假设励磁涌流为额定电流的1～12倍。

首先，利用变压器3D 有限元模型计算短路和空载合闸时变压器内部磁感应强度；然后，利用式（4）—式（15）分别计算两种情况下绕组受到的轴向力和横截面上的应力，结果如表2所示。

当励磁涌流为额定电流的6 倍和11 倍时，绕组上的轴向力分布如图9 所示，绕组横截面上的应力分布如图10所示。

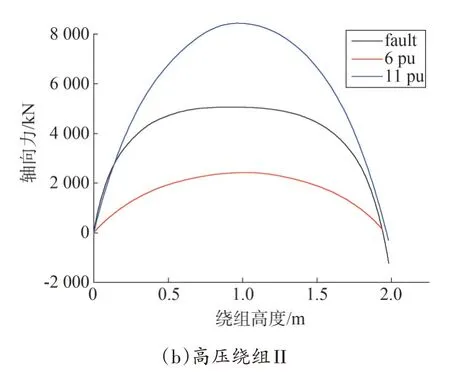
图9 高压绕组轴向力分布

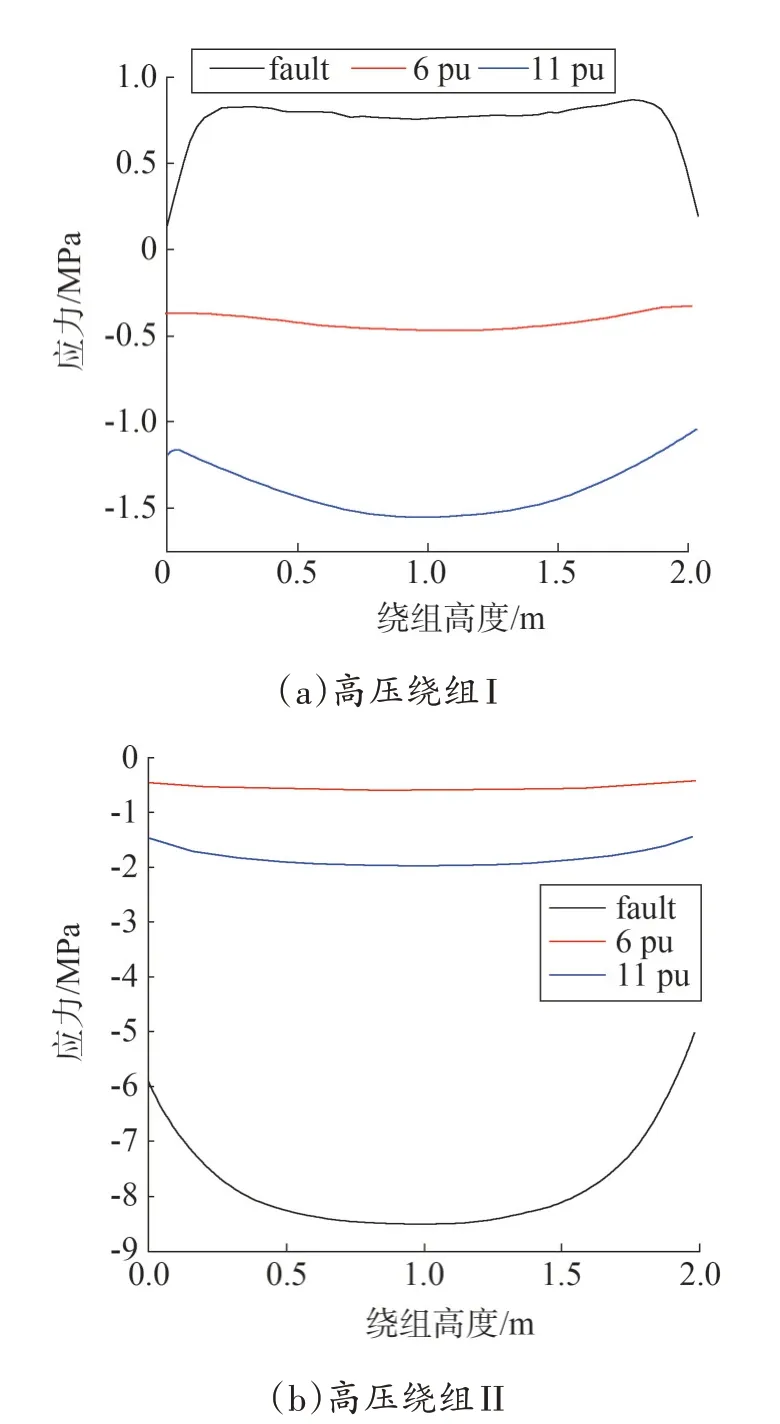
图10 高压绕组横截面应力分布

分析表2 以及图9—图10 可知，短路时，高压绕组I 受到压应力，受到的轴向力由中间指向两端；高压绕组II 受到拉应力，受到的轴向力由绕组两端指向中间。当出现励磁涌流时，高压绕组I 受到的应力和轴向力方向均发生改变，高压绕组II 受到的应力和轴向力方向未变，轴向力最大的位置位于绕组中间。

当励磁涌流变化时，记录高压绕组I和II受到的最大轴向力，并与短路情况下绕组受到的最大轴向力进行比较，如图11 所示，图中IIR为励磁涌流，ISC为短路电流。

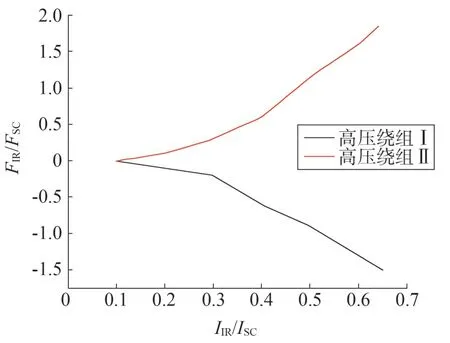
图11 短路和空载合闸时绕组轴向力比较

分析图11，当励磁涌流增大时，绕组受到的轴向力呈指数增长。高压绕组I受到的轴向力方向改变，当IIR＞50%ISC时，绕组内部受到的最大的轴向力FIR开始大于短路时的轴向力FSC。高压绕组II 受到的轴向力方向不变，当IIR＞45%ISC时，绕组外部受到的最大的轴向力FIR开始大于短路时的轴向力FSC。

5 结语

基于变压器3D 有限元模型，研究了励磁涌流作用下变压器高压绕组受力情况，研究表明：与短路时不同，励磁涌流作用下，高压绕组I 受到的最大轴向力由绕组端部变为绕组中部，且轴向力方向改变；高压绕组II中部受到的轴向力随励磁涌流的增长明显增大，励磁涌流只需要达到短路电流的45%即可产生相同的轴向力。

虽然励磁涌流一般小于短路电流，但励磁涌流出现频率和持续时间远高于短路电流，当绕组受力方向频繁改变，或者承受过大的轴向力时，就可能导致绕组松动变形、局部电场强度增大、绕组绝缘破坏，引起匝间或饼间短路。励磁涌流的破坏作用具有累计效应且不易察觉，是导致变压器故障的潜在因素之一。因此，有必要采用串联合闸电阻、选相合闸等方式抑制励磁涌流。