变电站巡检机器人航向信息融合算法研究

张 蒙，高 嵩，李 琛

（1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.国网山东省电力公司禹城市供电公司，山东 禹城 251200）

0 引言

传统的变电站主要依靠值班员进行人工巡检，存在意外风险发生频次高、巡视效率低等缺点［1-2］。随着自动化、物联网和人工智能等技术的迅速发展，使用机器代替人工，进行电力设备巡检已经成为数字化变电站的重要趋势［3-5］。其中，实时定位系统为巡检机器人的运动控制系统提供连续、实时、精确的位置、航向等导航信息，使其沿预定的路径行驶并完成检测任务［6-7］，是其实现高压设备智能巡检的关键技术之一［8］。

在变电站环境中，巡检机器人近似在二维平面中运动［9］。因此，相对于俯仰角和横滚角，对航向角的输出精度和输出频率有更高的要求。全球定位系统（Global Positioning System，GPS）可以为用户提供全球范围内的实时位置和速度信息［10］。GPS 定位基于卫星测距原理，没有累积误差，其长期性能优异［11］。但是，在变电站多遮挡和复杂电磁环境下，卫星信号容易受到干扰，使得定位性能下降甚至失效。另外，GPS 输出的航向角信息是根据载体的速度方向推算的，静止状态下航向角无输出。基于GPS 存在随机噪声、易受到干扰、只能动态输出航向等特性，单依靠GPS 传感器，无法满足巡检机器人对航向输出的精度、稳定性和连续性要求。光纤陀螺仪是一种可提供高精度高频率角速度输出的惯性器件［12］。通过对角速率进行积分可获得航向变化信息。陀螺仪的航向输出几乎不受外部干扰，具有良好的平滑度、较高的更新频率和短时精度［13］。由于通过积分获得航向变化，陀螺仪只能输出相对的航向信息，而且误差会随着时间的推移而累积，并且趋向于无穷大。GPS 和陀螺仪传感器单独使用时，优缺点鲜明；将两者恰当融合时，却具有良好的互补性。短时间内，陀螺仪的输出具有较高高精度和高连续性，可以校正GPS 的随机噪声，并在信号丢失期间提供航向保持［14］。GPS 作为一种全局定位技术，其提供的航向误差是有边界的，可以纠正陀螺仪的累积误差，改善其长期输出性能。

通过引入一种基于航向误差的自适应离散卡尔曼滤波器，融合GPS ∕陀螺仪传感器输出并获得航向信息。试验结果表明，该融合算法在动态和静态条件下都能获得高精度、高稳定性、高刷新率的实时航向输出，为巡检机器人的高精度路径规划和运动控制提供可靠的传感信息。

1 传感器输出及数据处理

1.1 GPS接收机

采用NovAtel 公司的ProPak-G2 GPS 接收机，其内置的OEMV-2板块能够捕获L1∕L2双频GPS信号，而且支持差分修正。两个双向的COM 端口，最高可支持230 400 bit∕s 串口通信速率。初始化完成后，能以最大20 Hz 的更新频率输出定位信息。该接收机的实体和具体接口如图1所示。

图1 NovAtel GPS接收机

ProPak-G2接收机有多种输出模式，可以通过串口向接收机发送不同的指令来完成不同的输出。本文采用它的BESTXYZA 的输出格式。该格式可以输出Wgs84 地心坐标系下载体的实时三维位置信息、载体的三维速度信息和位置精度因子的信息。图2展示了BESTXYZA格式下一帧典型的输出数据。

图2 1帧完整的BESTXYZA格式数据

在该模式下，GPS接收机可以输出载体的三维多普勒速度信息，即图2 中字母DOPPLER_VELOCITY后面的连续3 帧数据，其分别表示WGS84 地心坐标系下三维速度分量。

变电站机器人在地面近似二维平面运动，为便于计算，一般地，将GPS 接收机获得的地心坐标系WGS84 下的位置和速度信息转换到东北天ENU 坐标系中，航向信息可以通过速度分量进行反推［15］。公式为：航向=arctan（Vy∕Vx）。其中，Vy、Vx分别为由WGS84 坐标转换到ENU 坐标后，载体沿着Y轴（北向）、X轴（东向）的速度分量。

1.2 陀螺仪

陀螺仪能够测量车体的实时角速度。采用KVH公司生产的DSP3000 陀螺仪，如图3 所示。该陀螺仪采用成熟的光纤电路和全数字信号处理系统，能够有效消除零偏不稳定性和震动噪声。实际工程测试中，将KVH DSP3000 水平安装在机器人系统上，同时打开电源，在静止状态下，经过标定修正后每小时的零漂累积误差可控制在5°以内。

图3 DSP 3000陀螺仪

DSP3000 可以提供角度输出模式，直接为载体提供相对航向信息。上电后，陀螺默认输出的是角速率信息。只要持续向串口发送‘P’指令，即可切换到角度输出模式。陀螺仪的输出可选100 Hz或高达1 000 Hz，高更新频率保证精确捕捉短时间内的航向变化信息。

2 离散卡尔曼滤波器

卡尔曼滤波器是一种线性滤波器，它通过一系列递推数学公式描述，给出一种高效可靠的状态估计方法，而且使估计均方差最小。卡尔曼滤波器及其衍生算法在多传感信息融合中有着广泛的应用［16］。记系统的状态变量x∈ℜn，ℜn即n维的线性空间，其时间更新过程可以用离散差分方程表示，即：

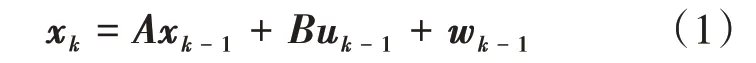
同时定义观测变量z∈ℜm。ℜm表示m维的线性空间。系统的量测方程可写为

式中：wk、vk分别为过程噪声和观测噪声；A，B，H表示转移矩阵；uk-1代表k-1时刻的系统输入。一般地，过程噪声wk和观测噪声vk是相互独立，并且服从正态分布的高斯白噪声，即：

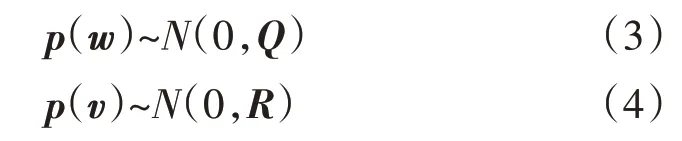
式中：Q和R分别是过程噪声和观测噪声的协方差矩阵。

卡尔曼滤波器通过反馈控制的方法来估计过程状态。具体来说，可以分为时间更新和量测更新两部分。时间更新方程通过前一时刻的系统状态和误差协方差，利用状态更新方程推算当前时刻的系统状态和误差协方差，完成对当前时刻状态的先验估计。量测更新则将先验估计与当前时刻的量测值结合，得到改进的后验估计。经过量测反馈校正得到的后验估计又会被用来推算下一时刻的先验估计，从而实现卡尔曼滤波器的反馈递归估计过程。

具体应用中，卡尔曼滤波一般由初始化、时间更新和量测更新3部分组成，估计过程如图4所示。其中表示k时刻状态变量估计的协方差矩阵，Kk表示k时刻的滤波器增益。x0、P0分别表示状态变量的初始估计值和初始估计协方差矩阵。

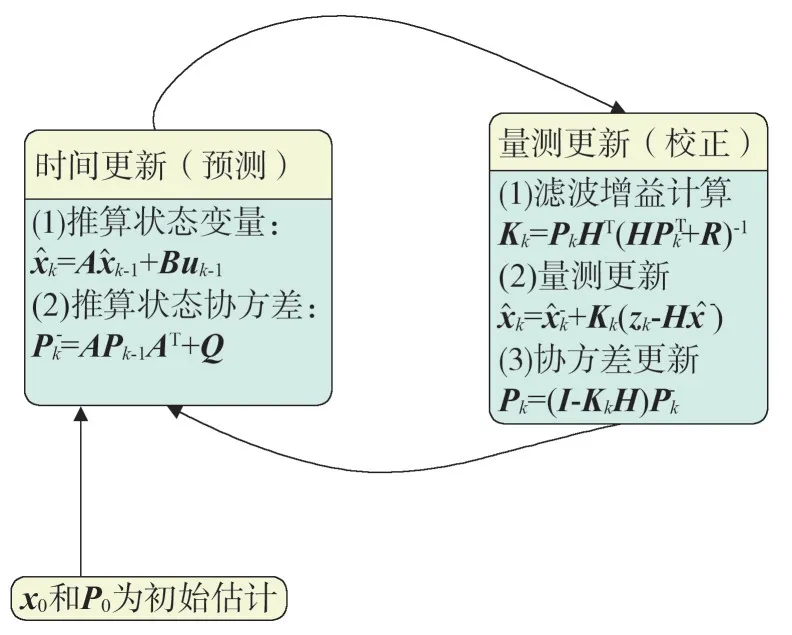
图4 卡尔曼滤波流程

要使用卡尔曼滤波器，首先建立估计变量的状态方程和量测方程。只有对系统状态建模准确，并对过程噪声协方差和测量噪声协方差进行正确的估计，滤波器才能准确估计状态变量，消除累积误差和随机噪声。

3 航向融合算法

GPS 接收机获得的航向估计只能在动态情况下使用，存在随机噪声且易受外界环境干扰。陀螺仪提供的相对航向信息输出稳定，短时间内精度很高，但存在累积误差，且在全局定位时需要初始化。通过建立恰当的离散卡尔曼滤波器，融合两系统的航向输出，使巡检机器人在动态和静态情况下都能获得精度高、稳定性好的航向输出。

3.1 滤波器建模

陀螺仪的航向输出可以看成由真实的航向和航向误差组成。采用间接卡尔曼滤波进行数据融合，将航向输出的系统误差作为估计量，通过估计系统误差间接获得对航向的融合估计。设GPS 和陀螺仪得到的航向信息分别为θgps和θgyro，则有：

式中：θ为真实航向；δθ为航向误差。将陀螺仪的航向误差作为系统估计变量，其航向误差主要由漂移累积误差和随机噪声两部分组成，离散化的系统状态方程可表示为

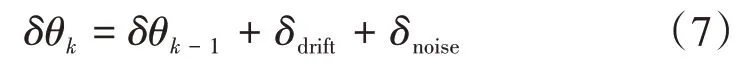
式中：δθk和δθk-1分别为k时刻和k-1 时刻航向误差的估计；δdrift为k-1 时刻到k时刻陀螺的累积误差；δnoise为k时刻的随机噪声。

由式（5）和式（6）可得系统的量测方程为

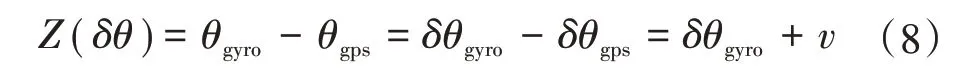
式中：v为量测噪声，即GPS输出航向的白噪声。

3.2 融合算法

建立估计系统误差的离散化滤波器模型后，可以按照卡尔曼滤波的一般过程，融合输出实时航向信息。

3.2.1 初始化

初始化即确定卡尔曼滤波状态变量和状态协方差的初始估计，为滤波递推过程提供初始值。根据滤波器建模，本文的初始化变量为陀螺仪输出的相对航向与Wgs84东北天坐标系下绝对航向的误差X0（δθ），其初始协方差矩阵P0。由于X0（δθ）和P0初始化后均为1×1阶矩阵，记为X0（δθ）和P0。

系统的真实航向为机器人相对于ENU东北天坐标系下的指北绝对航向。惯性器件获得航向的原理是依靠角速率积分，故只能获得航向的变化信息，即相对航向。要获得指北航向，只能依靠全球定位系统GPS的信号输出。

GPS 输出的实际上是位置信息，航向推算依靠的是位置变化带来的速度方向。当载体处在静止状态时，速度信息为0，只有在运动的情况下，才能通过GPS得到航向信息。

为尽可能保证初始航向的精确性，需要载体以一定速度运动，并且该段时间内GPS 信号良好。本文通过连续帧的自适应算法，实时估计GPS 航向信息的可靠性，确保航向误差的初始化的准确性，具体的算法如下。

航向滤波器初始化过程中，实时连续采集20 帧陀螺仪和GPS 得到的航向信息并储存在序列中，分别记为：

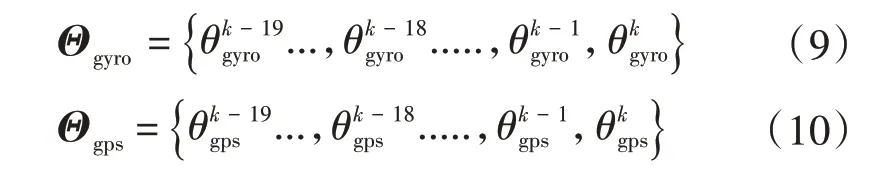
式（9）和式（10）相减，得到一组航向差值的量测序列为

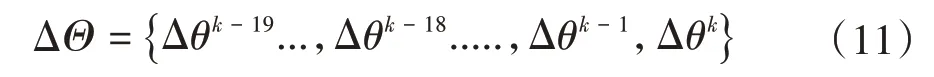
求取公式（11）中差值序列的均值和方差，作为滤波器的状态变量和误差协方差的初值。初始化过程中，实时存储连续n帧（本初始化算法中，取n=20）航向差值序列ΔΘ，并求取序列的均方差σΔθ。当方差小于一定阈值（2°），说明GPS 的航向估计已经较为精确，系统初始化完毕。将满足阈值条件的航向差值序列平均值作为滤波状态变量的初值，并将序列的方差作为误差协方差的初值，即：

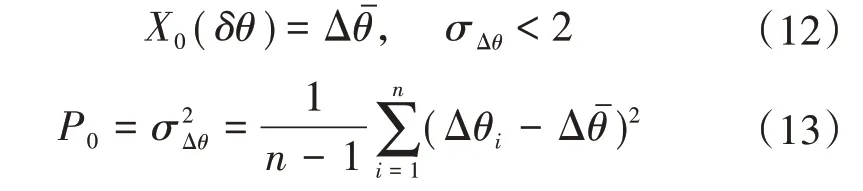
求取式（11）中差值序列的均值和方差，作为滤波器的状态变量和误差协方差的初值。初始化算法的流程如图5所示。

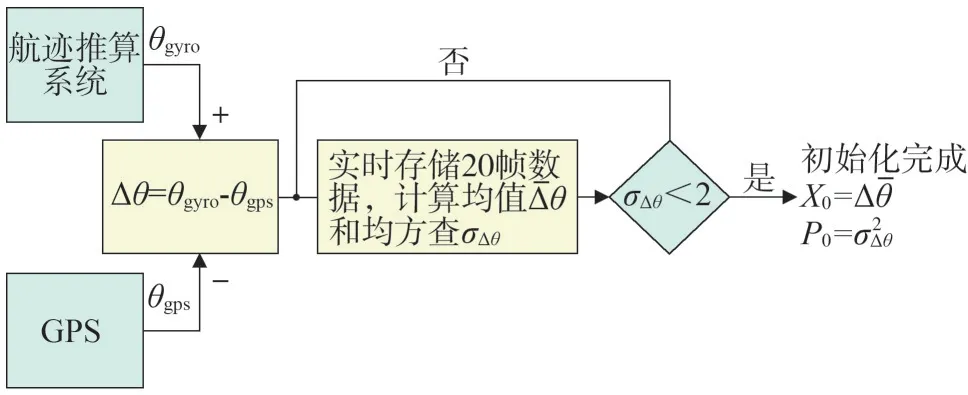
图5 滤波器初始化算法

为保证初始化算法的准确性，必须保证同步采集到GPS 和陀螺仪的每帧数据进行比对。在实际的工程实践中，由于GPS 和陀螺仪的数据更新频率存在差异，“同步采集”只能是一种离散化的近似。

由于GPS 的数据更新频率一般较低（采用的Novtel Propak-G2 GPS接收机，最大输出频率20 Hz），基于惯性器件的陀螺仪更新频率较高（采用的KVH DSP3000 陀螺仪可选100 Hz 或1 000 Hz 输出）。可以近似地认为：GPS 的输出是相对离散的，而陀螺仪的输出是近似连续的。数据同步过程将以GPS 输出为基准，采用多线程同步采集GPS 和陀螺仪的输出信号，每获得一帧GPS 数据，便抓取附近时刻的陀螺仪输出，作为近似的同步数据，以此类推，获得一组连续的数据比对帧。

实际上，本算法取航向差序列的帧数n=20，与GPS 接收机的最大输出频率20 Hz是一致的，即实际连续取得1 s内的GPS和陀螺仪近似同步序列。

3.2.2 滤波参数及滤波过程

因为采用一维估计，滤波器的系统方程和量测方程的转移矩阵为1×1的单位矩阵，即

系统的预测误差主要由累积误差和随机噪声构成。相比累积误差，实时的随机噪声是小量，可以略去。航迹推算系统的航向信息来自光纤陀螺的相对航向输出，累积误差δdrift以近似线性方式增长。经过静态试验标定后，陀螺每小时的零漂在7.2°，过程噪声协方差1×1矩阵Qk可以按式（3）和图4所示流程推导，即为

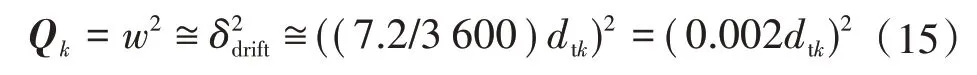
式中：dtk为陀螺仪更新的时间间隔。如果选取100 Hz的角度更新输出模式，时间间隔dtk=0.01 s。

为达到更好的滤波效果，采用统计的方法，较为精确的估计量测噪声。量测噪声的估计方法与滤波器初始化时所用方法类似。同时采集连续20 帧的航迹推算系统和GPS 测量得到的航向序列并做差，得到航向差序列，求取均值和均方差。短时间内，陀螺的零漂误差可以忽略不计，航相差序列的均方差可以近似作为系统的量测噪声，序列的均值则作为量测变量，即

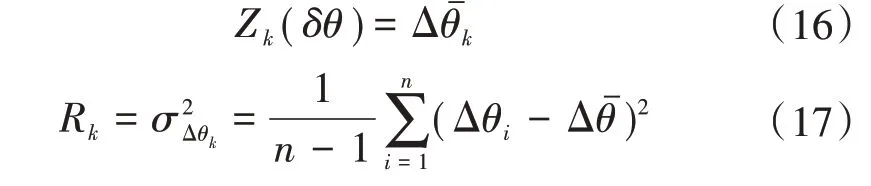
滤波器估计的是航迹推算系统的航向误差，航向误差主要是由光纤陀螺零漂造成的累积误差。相比GPS 航向测量的噪声，短时间内陀螺的累积误差很小；而且，GPS 对航向的测量受车速和GPS 接收信号的影响，测量精度并不稳定。因此在滤波时，没必要对每帧数据都进行量测更新。设定阈值为5°，只有当航相差序列标准差σΔθk＜5°时，才进行量测更新，校正系统变量和状态协方差矩阵。否则，只进行一步预测过程，维持航向误差不变，同时向前推算系统误差协方差。实时滤波流程如图6 所示。图中，Δθfilter表示经过卡尔曼滤波器融合后输出的航向角误差数据，θf表示最终输出的融合航向角信息。

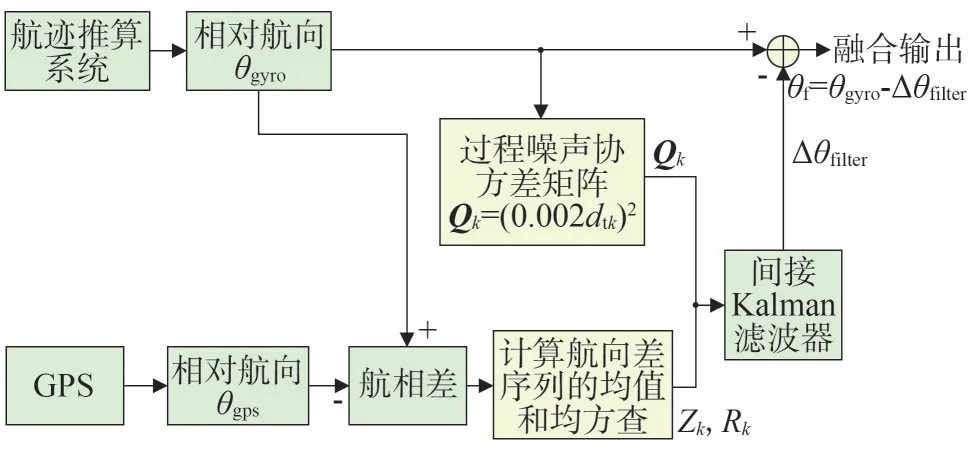
图6 实时滤波过程

4 试验结果分析

采用该融合算法进行实际测试。融合算法软件基于linux C++平台开发，分为数据解析、数据处理和数据发送三个模块。数据解析模块主要负责读取来自GPS、陀螺仪的数据包信息。数据处理模块则负责融合处理来自各个传感器的测量数据，数据发送模块负责将经过融合滤波处理的航向数据打包发送到机器人导航控制模块。因为要同时处理来自不同传感器的数据，为保证系统的实时性，满足多传感器和多任务的要求，结算软件采用多线程方式设计，利用linux 平台的并发性，采用多线程同时解析和处理多传感器的信息并进行数据融合。

在户外模拟变电站复杂环境进行实际运行试验，机器人最高运行速度控制在5 m∕s 以内。在滤波器初始化完毕后，得到单纯依靠GPS 测得航向和数据融合得到的航向结果如图7所示。

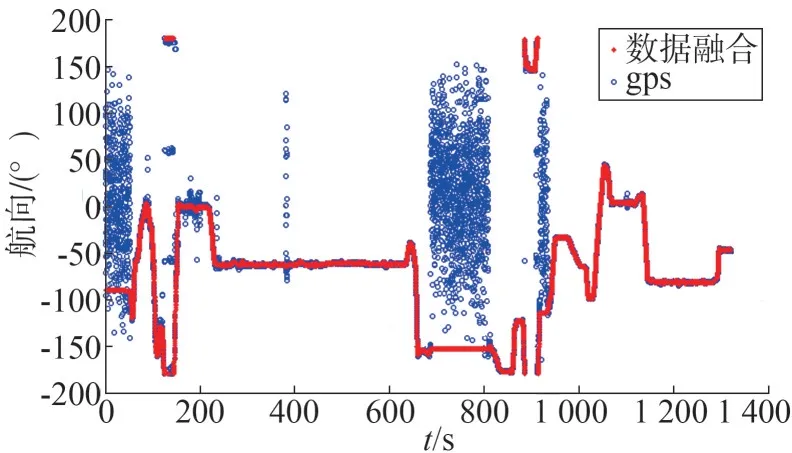
图7 航向对比

为了更全面的分析融合算法获得航向的效果，分别选取机器人从静止到启动、GPS信号较差和GPS信号较好3 种情况，对比融合航向输出和GPS 航向输出，结果如图8—图10所示。

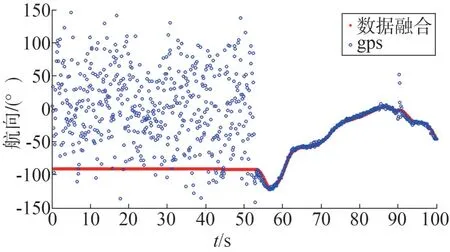
图8 从静止到启动状态下航向输出对比

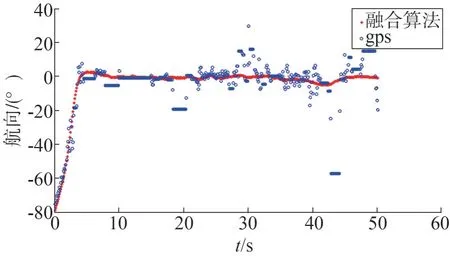
图9 GPS信号差情况下航向输出对比

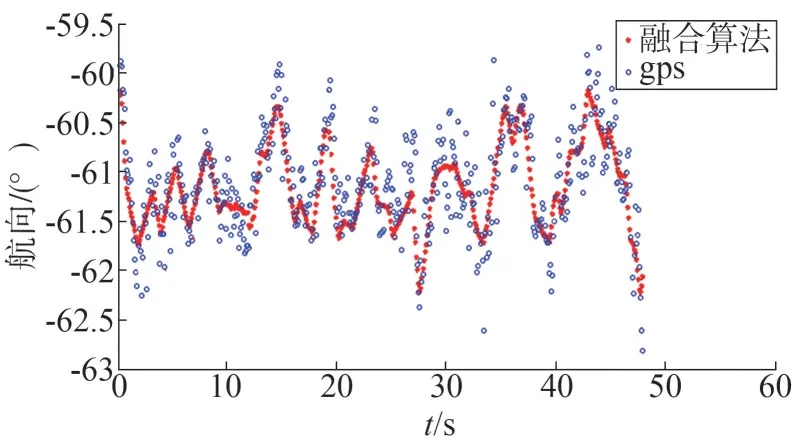
图10 从静止到启动状态下航向输出对比

由图8 结果可知，在静止状态下，单纯靠GPS 无法获得航向信息。然而，滤波算法融合GPS 和航迹推算的航向输出，即使在静止状态下也可以对车体的航向信息进行保持。车启动后，滤波算法得到的航向信息与GPS 测得的航向能够很好吻合，说明静态下航向保持的效果很好。

由图9 结果可知，在GPS 信号受到干扰情况下，依靠GPS获得的航向信息有很大的误差。依靠融合算法，可以有效消除抑制GPS的误差，即使在GPS性能很差的情况下，融合航向仍能保持较高的输出精度。

由图10 结果可知，在GPS 信号较好的情况下，能够输出较高精度的航向信息，但是仍存在随机噪声。通过融合算法得到的航向信息相对连续，能够有效消除随机噪声的干扰。

5 结语

提出了一种基于卡尔曼滤波的地面巡检机器人实时航向估计融合算法。通过GPS 信号修正陀螺仪的累积误差；同时，通过陀螺仪的稳定输出消除GPS输出的随机噪声和信号不稳定性。试验结果表明，该融合算法可以提高输出航向的准确性，鲁棒性，并在GPS丢失或静止状态下保持高精度的航向输出。