图像辅助汽车制动主缸补偿孔法线测量

赵长福，丁红昌,2 ，曹国华,2 ，侯 翰

（1. 长春理工大学 机电工程学院，吉林 长春 130022；2. 长春理工大学 重庆研究院，重庆 401135）

1 引 言

随着汽车的增多，汽车制动系统的可靠性研究成为汽车行业发展所要考虑的重要问题，目前，补偿孔式液压制动主缸仍为汽车制动系统的重要组成部分，制动主缸的作用是将驾驶员踩在制动踏板上的压力，通过真空助力器，传递到4个车轮的制动器上，以使汽车达到减速或者停车效果。汽车制动主缸补偿孔作为调节汽车制动主缸储液罐与压力室中制动液的关键部分，其尺寸精度和加工质量受到严格的控制。目前，有研究者通过机器视觉的方式对补偿孔的尺寸进行检测[1]，但由于丝杠进给方向与制动主缸轴线可能存在偏移，使得在对补偿孔进行采集时补偿孔成椭圆形，对于补偿孔的中心定位和尺寸拟合产生很大影响，因此如何垂直获取制动主缸补偿孔的图像，成为了广大工作者主要研究的问题。由于飞机钻铆孔的法线找正技术已经有很多的研究，因此考虑通过将飞机钻铆孔法线找正相关技术引入到对汽车制动主缸补偿孔的拍摄中，以获得更好的补偿孔图像。

在飞机的钻铆孔方面[2-5]，法线找正方式大体分为两大类：一类是接触式的法线找正算法；另一类式非接触式的找正算法。其中接触式的算法，主要以接触式位移传感器或者力传感器为主，通过传感器与工件表面接触来获得数据，然后对数据进行处理，解算出工件表面的法线方向。在非接触测量方面，主要借助激光测距传感器，测量传感器与待测工件表面的距离，经过算法处理，实现待测工件表面的法线检测。随着激光测距仪器水平的提高[6]，传感器的精度越来越高，体积越来越小，以非接触方式进行法线测量已经成为主流方式[7-8]。秦现生[9]等人提出三点快速调平算法，其测量精度在±0.5°以内，加工效率约为6个/min，适用于刚性托架基于有限曲面的加工区域，但是该算法需要移动待测工件，对于大型不易移动的工件，该算法具有一定的局限性。刘志刚[10]等人以微平面近似代替微曲面的方式，通过叉积的方式获得待测曲面的法向量，但是精度较低。公茂震[11]等人提出寻找平面与待测曲面的3条交线，通过在曲线上的待测点处求切向量，并用叉积的方法获得待测曲面的法线方向，可以将两个轴线的夹角控制在±0.5°以内，并且可以实现4°以内的矫正，最后通过内径千分尺对调整前后钻孔进行检测，发现孔的质量有所提高，但是该算法在求取曲面上的交线时计算复杂，不适用于实时性要求较高的场合。之后，应高明[12]等人利用4个激光测距传感器，获取工件表面特征点坐标，通过二次曲面拟合的方式逼近实际工件，通过对待测点求偏导数，获得该点处的法线方向。该方法对二次曲面的法线检测精度很高，但是对于非二次曲面而言精度不高。田威[13]等人提出一种新的法线检测算法，通过将空间中两个法线的夹角转换为两个投影面上的夹角，利用边角关系获得待测工件表面的法线，其垂直精度在0.5°内，并进行了误差验证。但是该方法仍然是将微平面替代微曲面的法线方向，存在一定的理论误差。国外，同样有研究者对曲面的法向量测量方法进行研究，他们除了采用激光位移传感器外，还将三维激光扫描仪应用到实际的曲面法线测量中，也取得了很好的效果[14-15]。RM Edgeworth[16]等人在三坐标测量机的基础上，采用三次样条插值模型作为自适应采样算法，实现了对曲面法向的测量。Calderon[17]基于局部分段平面邻域优化策略，提出了一种曲面法线的测量方法，该算法很大程度上提升了法线测量精度。近年来，随着新技术新方法的不断出现，姜春英[18]和毕超[19]等人相继提出了一种由相机和十字激光器构建的法相检测系统，后者法向测量精度可以达到±0.12。陈允全[20]等人提出一种激光跟踪仪与机器人相结合的大型扫描系统，该系统可以精确地获得大型工件的三维形貌以及自动完成工件外观参数的检测。虽然随着新方法新理论的不断出现，法线的测量精度也有所提高，但同时存在整体结构大而笨重、测量方法复杂等问题。

在现有的法线找正算法基础上，如何将其引入到补偿孔图像的法线找正中，并且使检测算法具有更好的效率以及更高的检测精度，成为一个待解决的难题。本文利用现有微平面近似代替微曲面算法的高效性，引入机器视觉技术，提高算法的检测精度，实现对曲面法线的找正。

2 曲面法线测量结构设计

汽车制动主缸补偿孔是深腔盲孔内侧壁上的小孔，直径为0.7 mm，图1为制动主缸的剖面图，主缸的主孔径在20~40 mm之间。将主缸装夹在自主研制的工装上，进行补偿孔参数检测，其中主缸实物图和检测示意图如图2所示。由于现有的激光测距传感器无法与相机组合伸入制动主缸的主孔中，因此，本文通过光纤将激光测距传感器的光线和视觉的图像系统导入进去，通过二维平移台以及垂直方向的丝杠进给运动，将检测设备深入到制动主缸内部，实现对补偿孔的法线找正以及对补偿孔的图像采集，具体结构如图2（b）所示。

图 1 制动主缸剖面图Fig. 1 Sectional view of a brake master cylinder

图 2 (a)制动主缸实物图和(b)制动主缸检测系统示意图Fig. 2 (a) Real picture of brake master cylinder and (b)schematic diagram of brake master cylinder detection system

汽车制动主缸补偿孔检测设备主要由3部分组成：第一，检测设备中的内窥镜采用的是硬性内窥镜，通过内窥镜的窥镜探头采集图像，并通过转向透镜将采集到的图像传送到相机的靶面上。第二，光纤的主要功能是将4个激光测距仪的光线导入制动主缸内部，并通过一个直角棱镜，将光线偏折90°，保证4个激光测距仪器的光线可以照射到补偿孔的周围。第三，补偿孔图像采集的照明方式采用主动式LED照明，由于LED照明具有结构简单、功耗低、发热低、高亮度、寿命长等优点，因此将贴片式LED光源环形贴于电路板上，具体位置如图3所示。

图 3 图像采集和测距系统Fig. 3 Image acquisition and ranging system

3 曲面法线测量原理

3.1 坐标系与法线模型的建立

假定相机所在平面为平面P，在相机周围正方形Z上均匀设置4个激光测距传感器S1、S2、S3、S4，并且4个激光器之间的距离相等即(S1S2=S2S3=S3S4=S4S1)，4个激光测距传感器的出射光平面与相机镜头在同一个平面P内，4个激光测距传感器的出射光线与平面垂直，以相机镜头的中点为原点O建立笛卡尔儿坐标系OXYZ，其中X轴垂直于S1S2方 向，Y轴垂直于S1S4方向，并且与X轴垂直，Z轴通过右手守则判定，为垂直于平面向下，具体如图4所示。

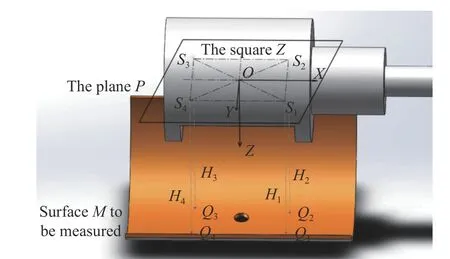
图 4 曲面法相测量示意图Fig. 4 Schematic diagram of surface normal phase measurement

通过建立坐标系，就可以分别确定4个传感器S1、S2、S3、S4的坐标，通过4个激光测距传感器测量到对应检测曲面的距离，就可以确定S1、S2、S3、S4对 应 的 投 影 点Q1、Q2、Q3、Q4的坐标。如图4所示，假定正方形的边长为2L，因此S1点 对应的坐标为(L,L,0)，根据正方形的性质，S2的 坐标为 (L,−L,0)，S3的 坐标为 (−L,−L,0)，S4的 坐标为 (−L,L,0)。根据4个激光测距传感器获得的距离值H1、H2、H3、H4，就可以确定4个投影点的坐标，即为Q1(L,L,H1)、Q2(L,−L,H2)、Q3(−L,−L,H3)、Q4(−L,L,H4)。

由4个投影点所确定的微平面，应用飞机钻铆孔法向量检测的办法，即利用微平面内两向量的叉积来获得微平面的法向量，具体公式为：

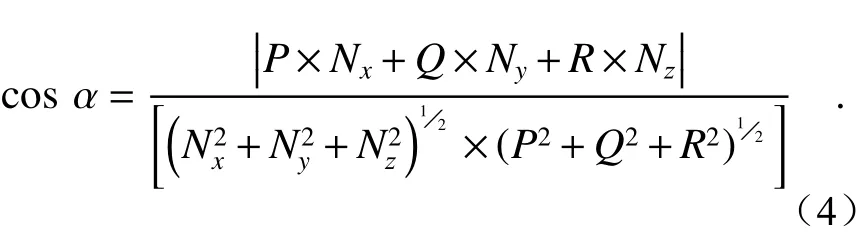
3.2 曲面法线测量误差分析

传统的基于四点微平面的法线检测方法是将曲面当成微小的平面来看待[21-23]，对于曲率较小的曲面来说可以适用，但是对于曲率较大的筒形工件来说，则存在较大的误差，具体误差分析如下：

其中A点位于圆柱筒的内侧壁上，如图5（a），所示，四点形微平面与A点的切平面平行，因此两个平面的法向量重合，此时通过4个激光测距传感器所确定的微平面法线代替曲面法线没有测量误差。但是在测量姿态改变后，如图5（b）所示，四点形微平面与A点的切平面并不平行，并且存在较大的倾斜角e，此时4个激光测距传感器所确定的微平面法向量与A点的切平面法向量存在一定的夹角，如图5（c）所示，如果用这个微平面的法向量去代替实际A点的法向量则存在较大的误差。因此我们发现只有当待测点位于4个激光测距点的中心位置时，四点微平面的法线才能代表待测曲面的法线。

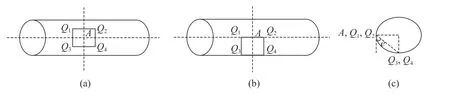
图 5 主缸补偿孔处四点微平面。（a）无误差；（ b）有误差；（ c）图（b）的侧视图Fig. 5 Four-point micro-plane at the compensation hole of the main cylinder. (a) Error free; (b) with error; (c) side view of (b)

为解决上述问题，提出四点微平面法线测量与机器视觉相结合的检测方式，通过相机采集4个激光测距点计算中心点K，并计算K与补偿孔圆心T的位置偏差，采用图像处理技术和运动控制相结合，保证激光四边形的中心位置与待测补偿孔中心重合，从而保证通过四点微平面所确定的法线，就是待测曲面补偿孔处的法线。通过手动设定曲面法线找正停止条件控制阈值β的大小，即使其在法线允许偏差角度内，具体角度值依据工作条件而定，β值越小，代表着精度越高，同时花费的时间就越长，反之找正速度越快，则精度相对不高。

具体算法步骤如下：（1）通过步进电机控制丝杠垂直进给到汽车制动主缸内部适当的位置。（2）光纤将4个激光测距仪的测量光线导入到汽车制动主缸主孔内部，均布在相机周围边长为2L的正方形上，并垂直于相机平面照射到制动主缸补偿孔所在曲面的周围，投影点为Q1、Q2、Q3、Q4，如图6所示。

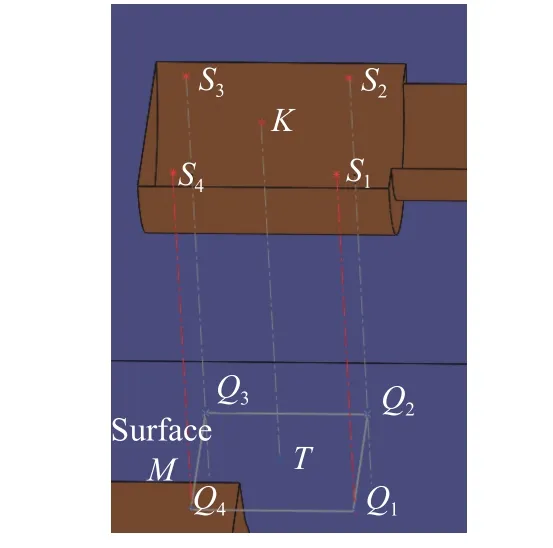
图 6 补偿孔法线检测剖面图Fig. 6 Normal detection profile of compensation hole

（3）拍摄制动主缸补偿孔的图像，通过图像处理中梯度霍夫变换技术，获得补偿孔的圆心T(x,y) ，计算补偿孔的中心T到四边形中心K的距离，通过运动控制卡控制二维平移台和丝杠的上下移动，使得两个中心点重合，如图7所示。

（4）获得4个激光测距点的距离H1、H2、H3、H4，代入式（3）确定微平面法向量，并计算两个面的法向量夹角α，将获得的角度反馈给伺服控制系统，通过伺服控制系统进行调节。（5）当角度α 小于阈值β后，即完成法线找正。否则返回步骤（3）进行迭代。（6）在完成步骤（5）之后，再通过相机采集汽车制动主缸补偿孔的图像，然后对补偿孔的参数进行检测，算法过程如图8流程图所 示。

图 7 补偿孔中心和四边形中心检测图Fig. 7 Compensation hole center and quadrilateral center inspection diagram

图 8 汽车制动主缸补偿孔法线找正流程图Fig. 8 Flow chart of normal alignment correction for the compensation hole of an automobile’s brake master cylinder

4 实验与验证

自主研制了高精度、高效率的运动控制机构和图像采集系统，并在该系统上进行实验[24]。本实验系统由高精度的举升机构、贴片LED主动照明系统、CCD相机、4个激光测距传感器以及导入光纤、自主研制的双远心内窥光路系统、自准直仪设备、电机以及软件处理系统组成。如图9所示，通过旋转丝杠使得举升机构带着CCD相机和光纤进入汽车制动主缸内部，点亮贴片LED主动照明系统并采集补偿孔曲面到相机平面的距离，通过软件采集到一幅主缸补偿孔的清晰图像，实时传输到计算机中。以ZDZG-22.2-12.385-1型号制动主缸为例，其补偿孔理论直径为0.7 mm，系统的主要技术指标如下：尺寸测量精度为±0.021 mm、分辨率为0.005 mm、测量时间为每件主缸从装夹到生成报告所用的时间不得超过2 min。

图 9 汽车制动主缸补偿孔光电检测系统实物图Fig. 9 Prototype of photoelectric detection system for compensation hole in an automobile’s brake master cylinder

具体设备选型如下：

（1）相机的选型

相机采用陕西维视数字图像有限公司的MV-VS078FM/FC型彩色面阵CCD相机，相机的分辨率为1024 pixel×768 pixel，图像传感器尺寸为1/3英寸，帧速率为30 frame/s，由相机像元尺寸以及相机镜头的放大倍率可以确定相机的物方分辨率为0.002 mm，比系统要求的0.005 mm更高，因此满足系统分辨率的要求。

（2）双远心镜头设计

常见的远心镜头一般体积庞大，无法直接进入制动主缸内部，本课题组研制了一种物方像方双远心镜头。该镜头由物镜和转像透镜共同组成远心内窥光路，由于制动主缸补偿孔并不位于内窥镜的轴线上，因此在内窥镜的前端加装90°视向棱镜对光线进行偏折，实现对补偿孔的采集。本文研发的双远心镜头为固定焦距，焦距为48 mm，固定工作距离，距离为20 mm，成像圆直径为6 mm，放大倍率为2.4倍，空间分辨率为107 lp/mm。

（3）激光测距仪选型

4个激光测距仪采用的是奥泰斯公司的CD22-100-485型激光测距传感器，它的测量波长为655 nm，测量距离为100 mm，最高分辨率为1 μm，当测距仪器产生1 μm误差时根据式(1)~式(4)知，变换到补偿孔图像上的长度为0.002 mm，满足系统分辨率要求。

（4）自准直仪选型

自准直仪选用奥特梅尔光电科技有限公司的光电自准直仪，型号为AUTOMAT ULTRA，其测量精度在±100″内可以达到±0.5″，测量分辨率为0.1″，重复性为0.2″。当自准值仪器误差为0.1″时，补偿孔图像上只产生0.0006 mm的误差，远高于系统分辨率。通过使用光电自准直仪可以测量各种敏感仪器的轴向矢量，因此可以对丝杠的轴向进给误差进行检测。

（5）丝杠选型

滚珠丝杠作为本系统的高精度传动部件，选用天津海特公司精度等级为P5级的FK2505型滚珠丝杠，其螺杆外径为20 mm，丝杠螺距为5 mm，步距角为1.8°，细分数为40，额定动载荷为13.1 kN，额定静载荷为20.2 kN。丝杠进给的偏差角越大，系统测量的误差就越大，当偏差角产生0.01°的变化时，系统误差为0.0035 mm，同样高于系统的分辨率要求。

4.1 本文算法找正精度验证

首先通过步进电机控制丝杠进给到适当位置，通过软件触发进行图像采集，然后对采集到的图像进行预处理，通过中值滤波算法去除图像中的噪声，然后使用梯度霍夫变换，通过投票机制获得圆心所在位置，并计算该点与4个激光测距点中心的偏差，如图10所示。图中两个小的十字线分别代表补偿孔的中心位置以及4个激光点的中心位置，图像的左上角显示了两个中心点的坐标值，分别计算两个中心点的水平像素差值和竖直像素差值，通过对像素进行标定[25-26]，将像素值转换为实际的距离值，然后把偏差结果反馈给运动控制系统，接着，通过平移和旋转运动，使得两个中心点重合，此时四边形平面与补偿孔中心点的切平面平行，法向量方向相同，可以进行曲面法线计算。将测得的各个激光测距传感器的距离H1、H2、H3、H4，带入式（1）~式（3）计算此时补偿孔所在位置的法向量N，然后，通过式（4）计算该法向量与相机镜头法向量Ns的 夹角α ，将α值作为两个法向量夹角的测量值。通过实验获得Q1(5,5,20.03)、Q2(5,−5,20.07)、Q3(−5,−5,20.04)、Q4(−5,5,19.99)， 由此可知将所获得的带入式(3)中，得到法向量已知那么通过式（4），可得夹角α为0.32°。

图 10 补偿孔中心位置与四边形中心位置偏差Fig. 10 Deviation between the center of the compensation hole and the center of the quadrilateral

为了验证本文算法获得的法向量夹角的精度，使用奥特梅尔光电科技有限公司的AUTOMAT ULTRA系列光电自准直仪测量丝杠进给角度的偏差，来求解镜头法向量与制动主缸补偿孔法向量夹角α的理论值。具体方法如下：

（1）通过自准直仪建立空间测量系统，利用其自准直功能，实现对立方镜的测量，从而将丝杠轴矢量方向转换到机械坐标系下进行测量。

（2）测量时，使用一台自准直仪，将自准直仪安置在稳固的基座上，通过调整底部的调平旋钮将自准直仪调平，然后取下自准直仪物镜保护盖，通过电脑上安装好的软件实现水平方向（X轴）和竖直方向（Y轴）的角度测量，图11为实验现场图片。由自准直仪发射出平行光照射到立方镜上，通过立方镜的反射，经过物镜后在焦平面上形成分划板标线像与标线重合，就可以算出立方镜的微小倾斜角。

图 11 实验现场图片Fig. 11 Experimental site

（3）通过测量初始立方镜的角度，丝杠带着立方镜进给到指定位置后，测量此时的立方镜角度，就可以通过软件计算此时丝杠的轴线偏差，也就是相机的法线理论偏差，结果如图12所示。

图 12 软件界面显示测量结果Fig. 12 Measurement results displayed in software interface

通过本文算法计算的法向偏差与自准直仪计算的法向偏差进行比较，多次实验结果证实本文算法鲁棒性好，检测精度如图13曲线所示，可以看出本文法向偏差角度检测算法的误差小于0.05°，满足工业现场的精度要求。

图 13 多次测量汽车制动主缸补偿孔法线找正精度Fig. 13 Multiple measurements of the normal alignment accuracy of the compensation hole of the automobile’s brake master cylinder

4.2 本文算法对补偿孔不圆度的影响

由于相机没有对补偿孔进行垂直拍摄，会导致补偿孔的图像成椭圆型，因此通过对补偿孔图像进行不圆度检测，可以判断算法的效果，并计算每种处理算法所用的时间。

不圆度的计算公式为[27]：

其中Rmax和Rmin分别是制动主缸补偿孔的最大半径和最小半径，R为最大半径和最小半径的平均值。现有的椭圆拟合方式主要有3种：基于Hough变换的椭圆拟合方法，基于不变矩的方法，基于最小二乘的椭圆拟合方法。由于最小二乘法是在随机误差为高斯分布时，由最大似然法推出的一个最优估计技术，它可以使测量误差的平方和最小[28]。因此本文采用椭圆拟合的方式计算出最小半径和最大半径。

椭圆曲线的一般表达式为[29]：

设拟合目标函数为：

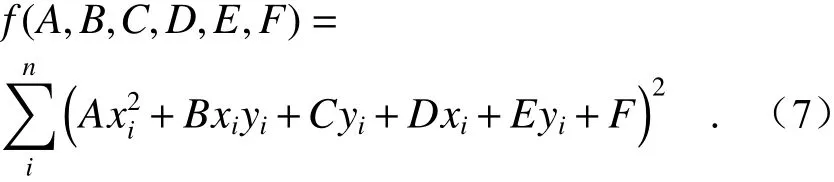
为使目标函数最小，可以通过对各个变量求偏导数：

求解方程，便可以确定椭圆方程的系数C、D、E、F的值，就可以确定椭圆方程，从而确定椭圆的长半轴和短半轴的值。椭圆长短轴和系数A、B、C、D、E、F的计算公式为：

A、B、

最后，通过对4种采集方式进行图像摄取，拟合出补偿孔的椭圆图像，标识出Rmin和Rmax，对没有法线找正的补偿孔进行拍照，如图14所示。从图中可以看出，由于没有进行补偿孔的法线找正，所获得的补偿孔成椭圆形，对于下一步的补偿孔参数检测存在较大的影响。对只用四点微平面进行法线找正进行拍照，如图15所示。可以看出相比于没有进行补偿孔法线找正的图像，其不圆度存在明显改善。通过二次曲面拟合算法对图像的法线进行矫正，结果如图16所示。从图中可以看出：拟合的椭圆效果较好，不存在明显的长短轴。本文算法结果如图17所示。从图中可以看出，通过向量叉积与图像处理算法相结合的方式获得的补偿孔在不圆度上有了很大的改善，通过式（10）计算得到4种方式获得的补偿孔不圆度，如表1中不圆度一栏所示。检测4种方法的法线找正精度，第一种为没有进行法线找正，当内窥镜到达指定位置时，自准直仪的数值偏差较大，并将其记录在表中，将微平面法线找正、曲面拟合找正算法和本文算法的法线找正结果分别与自准直仪获得的法向量偏角做差，将其作为误差，记录在表格法向误差一栏。通过本文算法修正后对补偿孔进行拍摄，可以看出所获得的补偿孔圆度更好，由于基于激光测距的法线找正算法和图像处理算法采用的是并行处理办法，因此检测时间与基于叉积的微平面法线找正算法的检测时间相差无几，并且所用时间少于曲面拟合算法，满足在线检测要求，可以说本文算法在满足实时性的前提下，可以获得更高的检测精度。同时通过观察表1中的不圆度和法向误差两栏，可以看出法向误差和补偿孔的不圆度成正相关，即法线找正精度越高，所获得的补偿孔的圆度越好，越有利于对后续补偿孔参数的精确检测。

以ZDZG-22.2-12.385-1型号制动主缸为例，其补偿孔理论直径为0.7 mm，尺寸测量精度为±0.021 mm，观察表1中的第一行，直接获取的补偿孔图像的不圆度为0.23，补偿孔检测直径为395.43 pixel，而补偿孔理论直径为351 pixel，标定图像中一个像素所代表的实际尺寸为0.002 mm，由于相机法线没有垂直于补偿孔获得图像，利用图像对补偿孔尺寸精确检测会产生大约0.09 mm的误差，尺寸检测精度低于精度指标要求，因此说明对补偿孔法线找正的必要性。

表 1 4种汽车制动主缸补偿方法的孔不圆度、误差大小和时间Tab. 1 Out-of-roundness, error and time of compensating hole of automobile brake master cylinder by four methods

图 14 未经过法线找正图像Fig. 14 Uncorrected image

图 15 四点微平面法线找正图像Fig. 15 Normal alignment image by four-point microplane method

图 16 曲面拟合法线找正算法Fig. 16 Normal alignment image by curved surface fitting algorithm

图 17 本文算法图像Fig. 17 Normal alignment image by proposed method

通过本文算法找正后获得的制动主缸补偿孔图像的不圆度约为0.0073，圆度有了很大提升，此时补偿孔的检测直径为351.78 pixel，与理论值相差0.78 pixel，实际产生的误差仅为0.00156 mm，满足精度要求。在现有补偿孔法线检测方法中加入本文算法同样可以满足工业上实时检测的需求。由此可知，本文检测算法在满足高精度的同时也满足了在线检测的需求。

5 系统主要误差来源及分析

任何实验系统都存在不可避免的系统误差，我们要做的就是尽可能地减小测量误差，要实现这个目的，就要对误差来源，以及各种误差在总误差中所占的比重进行详细分析[30]。通过多次实验验证本文找正算法的误差精度小于0.05°，误差较小。对实验系统的主要误差源进行分析：

（1）光学系统误差

由于本文的相机镜头为物方像方双远心镜头，其放大倍率为恒定的，所以不存在光学放大倍率误差，因此本系统的光学误差σ1主要以图像畸变误差为主。

误差σ1主要是由透镜制造精密度和安装位置偏差引起的，图像畸变主要分为两大类：一类是径向畸变，一类是切向畸变。以径向畸变为例，其中成像点在径向可以表示为：

式中 (x0,y0)表 示图像中畸变点的位置， (x,y)表示图像无畸变时的位置，k1、k2、k3代表畸变系数，r表示到畸变中心的距离，通过计算，畸变系数为0.004，因此，本系统的光学畸变为：σ1=0.7×0.75×0.004=0.002 1 mm。

（2）机械系统误差

由于系统传动装置采用的是滚珠丝杠，其在传动过程中必然存在导程误差。本系统选用的丝杠螺距为5 mm，步距角为1.8°，细分数为40，导程为5 mm，那么导程误差σ2为：

式中：θ为步距角，n为 细分数，P为导程值。将滚珠丝杠的参数带入式（12），通过计算可得σ2为0.0005 mm。

（3）系统随机误差

系统随机误差是指在测量过程中由于微小波动而对测量结果产生的影响。在本系统中的随机误差σ3主要是由不规则振动和温度误差引起的。

在图像辅助制动主缸补偿孔法线测量中由于丝杠的进给运动，会产生一些不规则的振动，这些振动只能尽量抑制，而不能彻底消除，但是通过实验发现，这些振动对于法线找正误差的影响很小，基本可以忽略不计。

由于所有物体都有热胀冷缩的特性，所以在不同温度环境下，汽车制动主缸尺寸会受到影响，进而使补偿孔的法线测量受到影响，因此如果检测时的温度不明确，这样的法线测量是没有意义的。我国标准温度规定为20 ℃，但是一般实际工作环境都不是20 ℃，因此一定会对测量结果产生影响，具体影响公式为：

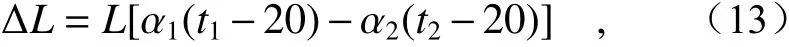
式中L代表被测量的尺寸，ΔL代表测量的误差，α1代 表工件材料的膨胀系数，α2代表检测仪器的膨胀系数，t1代 表工件的温度，t2代表测量仪器的温度。由于实验现场的环境为实验室空调条件，温度变化不大，因此由于温度引起的误差同样也很小，可以忽略不计。

基于上述对系统误差的分析，可以得到系统的总误差σa：

式中σa为 系统的总误差， σi(i=1,2,3)为各个部分的分系统误差。将各部分误差代入式（14）中即可计算出系统总误差σa

为0.00216 mm。补偿孔的圆心与4个激光点的中心存在不完全重合误差，激光测距仪的4个距离值也存在误差，将其换算成法线测量的偏差角θ，公式为：

由于θ 角较小，所以 θ与其正切值近似相等，σa为系统的总误差，H为4个激光器的平均距离，将结果带入式(15)，计算得偏差角度为0.026°，小于0.05°。本文法线测量系统的误差精度在允许范围内，满足系统找正要求。

6 结 论

本文在经典的四点微平面测量法线的基础上，与图像处理算法相结合，解决了用微平面代替曲面时存在误差的问题。通过实验验证，本文算法在对汽车制动主缸补偿孔进行图像采集时，保证了镜头法线和待测补偿孔的法线之间夹角与理论值偏差小于0.05°，通过对修正前后补偿孔的不圆度进行比较，说明本文算法可以有效改善相机不能垂直摄取补偿孔图像问题。本文算法计算速度快，精度高，满足工业现场对于实时性和高精度检测要求。