Photon-assisted Fano resonance tunneling periodic double-well potential characteristics

ZHANG Yong-tang

（1. School of Computing, Guangdong Neusoft Institute, Foshan 528225, China；2. Institute of Cooperative Sensing and Advanced Computing Technology,Nanchang Technology Institute, Nanchang 330003, China）

* Corresponding author，E-mail: gov211@163.com

Abstract: Optical properties of periodic double-well potential are one of the frontier research fields in laser physics and quantum optics. In this work, we have employed time-periodic double-well potential for the investigation of Fano-type resonant tunneling of photon-assisted Dirac electrons in a graphene system. Using a double quantum well structure, it is found that the resonant tunneling of electrons in a thin barrier between the two quantum wells splits the bound state energy levels, and the Fano-type resonance spectrum splits into two asymmetric resonance peaks. The shape of Fano peak is regulated by changing the phase, frequency, and amplitude, that can directly modulate the electronic transport properties of Dirac in graphene. Our numerical analysis shows that the relative phase of two oscillating fields can adjust the shape of the asymmetric Fano type resonance peak. When the relative phase increases from 0 to π, the resonance peak valley moves from one side of the peak to the other. In addition, the asymmetric resonance peak becomes symmetric at critical phase 3π/11. Furthermore, the distribution of Fano peaks can be modulated by varying the frequency and amplitude of oscillating field and the structure of the static potential well. Finally, we suggest that these interesting physical properties can be used for the modulation of Dirac electron transport properties in graphene.

Key words: physical optics; resonant tunneling; photon-assisted tunneling; dirac electrons; quantum optics

1 Introduction

Graphene, as a new class of 2D material, has attracted extensive research interest due to its unique properties and wide range of applications in nanoelectronic devices[1-3]. The electronic band structure of graphene near the Fermi energy is linear and gapless, and the dynamic characteristics of low-energy electrons can be described by a 2D Dirac equation without mass[4-5]. Therefore, many relativistic particle properties are shown such as the Zitterbewegung effect[6-7], Klein paradox[8-10], and Klein tunneling[11-13]. Among these, Klein tunneling is a relativistic tunneling effect. Dirac fermion[5]can completely tunnel through extremely high and thick barriers. On the other hand, Pereiraet al.have reported that momentum parallel to the barrier can inhibit Klein tunneling, thus allowing the restriction of Dirac electrons in graphene[14]. Recently, the transport properties of Dirac electrons in graphene in various potential fields have attracted extensive attention[15-20].

Besides, the transport properties of the periodic field-driven quantum tunneling are also a crucial research topic. Fano resonance[21-23]appears in this type of periodic field-driven quantum tunneling,which originates from the quantum interference effect of continuous and bound states. When the quantum exchange energy occurs between the electron and the oscillating field, the photon-assisted tunneling effect will occur[24]. So far, the photon-assisted Fano-type resonant tunneling effect in semiconductor heterojunction has been widely studied[25-27].Recently, some of the reports show that the quantum behavior of relativistic fermions in a strong field is significantly different from that of non-relativistic particles[28-32]. In general, many interesting quantum transport phenomena in graphene are related to energy. Photon-assisted Dirac electron transport is a powerful tool for the quantitative detection of energy-related transport in graphene[33].

Recently Ref. [34] has theoretically proved that the Fano-type resonance can also be produced when the electrostatic potential of graphene is added to the oscillating field. In this paper, we extend the work Ref. [35] to a time-dependent double-well potential structure. Using the Floquet scattering matrix theory, we studied the Fano-type resonance tunneling of photon-assisted Dirac electrons in graphene timesymmetric double-well potentials. In contrast to the single-well potential structure[36-37], the energy levels of the bound states split into two asymmetric formants in the double-quantum well structure. The reason behind this is the thin-barrier resonance tunneling of electrons between the two quantum wells. We found that the relative phase of the two oscillating fields modulates the shape of the Fano peak. Furthermore, the numerical simulations show that the shape of the Fano peak is also related to the frequency and amplitude of the oscillating field and the structure of the potential well.

2 Models and methods

We consider the tunneling of Dirac electrons through a time period double-well potential. This time period double-well potential structure can be realized by applying two local gate voltages and two small Alternating Current (AC) voltages to graphene. From left to right, electrons pass through five regions Ⅰ, Ⅱ, Ⅲ, Ⅳ, and Ⅴ, as shown in Fig.1.

Fig. 1 Sketch model of Dirac electron transport through a double-well potential and two applied oscillating fields. V0 is the depth of the static well; d is the width of wells, a is the thickness of barrier. V1 cos(ωt + α) and V1 cos (ωt + β) are the applied oscillating fields

The time cycle potential can be expressed as

whereV0(<0) is the depth of the static potential well,V1, ω and α (or β) are the amplitude, frequency, and phase of oscillation field, respectively.The movement of Dirac electrons through a time period double-well potential can be described by the time-dependent Dirac equation as:

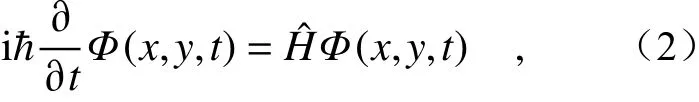
whereHˆ is the massless Dirac Hamiltonian that can be expressed as

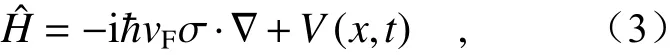
where σ=(σx,σy) is the Pauli spin matrix[11],vF≈1.0×106m/s is Fermi velocity[12].

According to the Floquet scattering theory[12,38],the formal solution of Eq. (2) isΦ(x,y,t)=ϕ(x,y,t)exp(−iEFt/h¯) . WhereEFis the eigenvalue of Floquet energy, and ϕ(x,y,t)=ϕ(x,y,t+T) is a time-periodic function with a period ofT=2π/ω.Thewavefunctioncomponentϕ(x,y,t)along theydirectioncanbe expressedasatypeof expof wave vectorycomponentky. This is due to translational symmetry along theydirection. In the case of given incident energyEandky, the electron wave function in the well region Ⅱ and Ⅳ can be expressed as

Herel= Ⅱ, θ =α, andl= Ⅳ, θ =β. Jnis a Bessel function of first kind,sn=sgn(E−V0+nh¯ω),φn=arctan(ky/kn) , andkn=Since Dirac electrons incident on the oscillating field is inelastically scattered to numerous Floquet channels, the outside wave function of the potential well region can be expressed as the superposition of waves with all energy values. Therefore, the wave functions of areas Ⅰ, Ⅲ, and Ⅴ is

wherei=Ⅰ, Ⅲ,The energy of incident and outgoing waves in the sideband isEn=E+nh¯ω (nis sideband index), whereEn<0is the attenuation mode. This is due to energy exchange between the electron and the oscillating field and takesh¯ω as the unit. Since the imaginaryknmode do not propagate, the corresponding sidebands are called attenuation sidebands[15,39].

Using the continuity conditions of wave function at the boundariesx=0,d,d+aand 2d+a, the scattering matrix of Dirac electrons tunneling in the double-well potential can be expressed as[35]

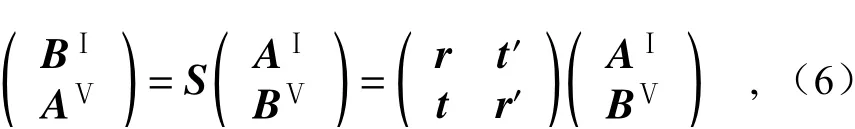
whereAⅠandBⅤare coefficient vectors that con-

According to the Landauer-Buttiker formula[16,40],the conductance of electron through the double-well potential can be obtained as

3 Numerical results

In this section, we numerically investigate the Fano-type resonance tunneling of photon-assisted Dirac electrons in a graphene-containing doublewell potential, followed by its conductance simulation. The minimum sideband indexNof equations(7) and (8) is obtained from amplitude and frequency of the oscillating field. The result can be c onverged bytakingN>V1/h¯ω.Afterthis, wetookn=0,±1,±2whichisfollowedbyThe structural parameters of a static well ared=200 nm,a=40 nm, andV0=−50 meV. The calculated results became single quantum well atd=150 nm anda=0 nm.

The relationship between conductanceGand incident energyEof the oscillating field at different amplitudes is shown in Fig. 2(a), whereky=0.006 nm−1and phase α=β=0. In Fig. 2(a), a smooth black solid line shows Klein tunneling in the absence of oscillation field (i.e.V1=0). This Klein tunneling is caused by the electron-hole conservation in graphene[12,40]. When two time-dependent oscillatory fields are applied, the photon-assisted resonant tunneling is generated and sharp asymmetric Fano resonance peaks appeared. This arises from the interaction of Dirac electrons and the oscillatory field. The asymmetric Fano-type resonance originates from the quantum interference between continuous and discrete (bound) states. When the incident Dirac electron passes through the first potential well, it emits a photon and falls in the bound state.After this, it absorbs a photon and returns to the incident channel or other Floquet channels of tunnel via the second potential well. This photon-modulated tunneling process creates a discrete channel in Fano-type resonance. When the energy of the incident Dirac electron is increased by one or more photons from that of a bound state of the doublewell potential, a single photon or multi-photon resonant transmission occurs.

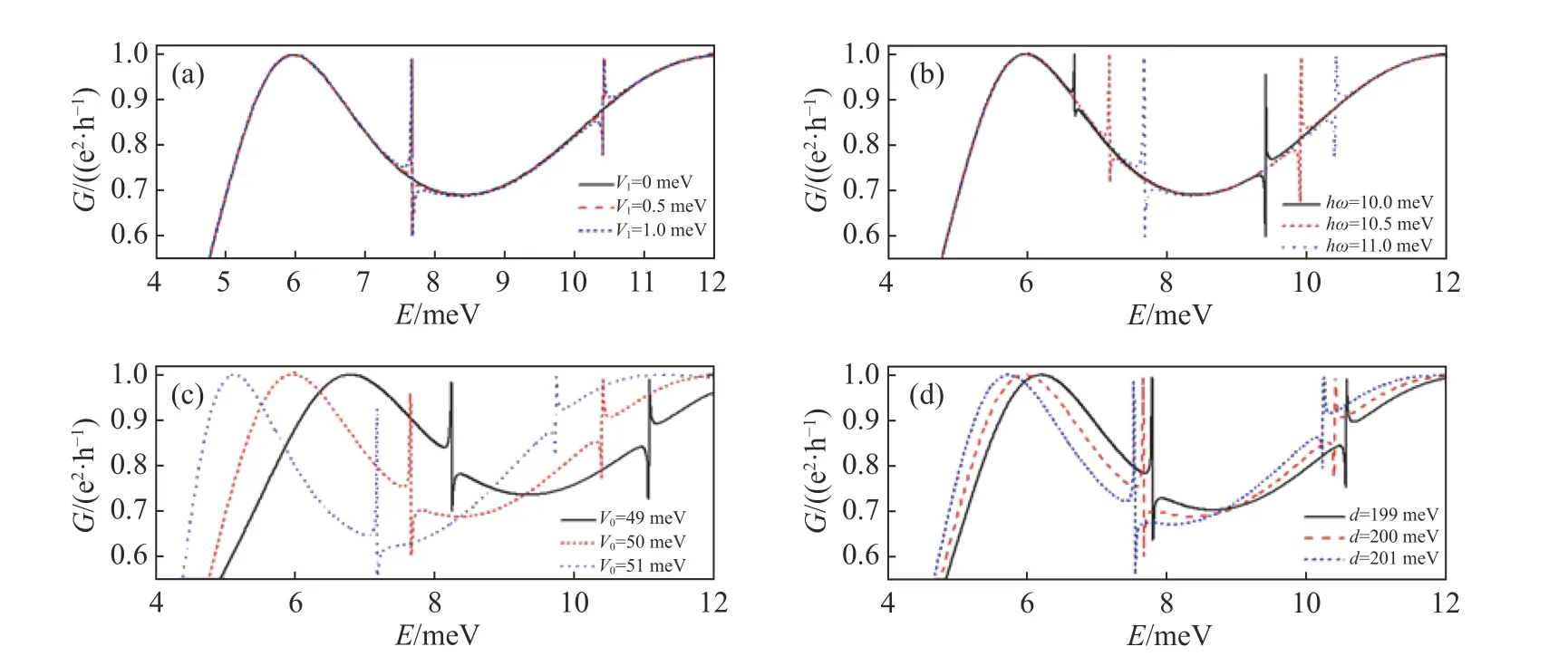
Fig. 2 Fano-type resonance in conductance G for α=β=0, a=40 nm ， ky=0.006 nm−1. (a) ћω =11 meV , V0=−50 meV，d=200 nm ; (b) V1=1.0 meV, V0=−50 meV ， d=200 nm ; (c) ћω =11 meV ， V1=1.0 meV, d=200 nm; (d) V1=1.0 meV，ћω=11 meV ，V0=−50 meV.

Previously, the Fano-type resonant tunneling of photon-assisted Dirac electrons in time-dependent single-well potential has been reported[36-37]. The Fano-type resonance spectrum is different from the single-well potential structure and can be divided into two asymmetric resonance peaks. This is because of the splitting of bound state energy levels, caused by resonant tunneling when electrons pass the thin barrier between the two quantum wells. Therefore,whenV1=0.5 meV andh¯ω=11 meV as shown in Fig. 2(a), then two asymmetric Fano resonance peaks are appeared atE1≈7.65 meV andE2≈10.43meV, respectively. In the absence of an external oscillation field, the binding energy of double-well potential can be calculated asEb1=−3.347 meV andEb2=−0.575 meV, respectively.So, it is found that resonance energy satisfies the single-photon assisted Fano-type resonance transmission relationE1(2)−Eb1(2)=h¯ω. In fact, the amplitude of oscillating field determines the coupling strength between the incident Dirac electron and external oscillating field. Furthermore, the width of Fano-type resonance peak gradually widened along with the increase of amplitude of oscillation field, as shown in Fig. 2(a).

Interestingly, we observed that the shapes of these two Fano peaks are different as can be seen in Fig. 2(a). In the case of first resonance peak (atE1≈7.65meV), a sharp peak is followed by a sharp valley. While a sharp valley is followed by a sharp peak in the case of second resonance peak (atE2≈10.43meV). According to Fano theory, the lineshapeofFano resonanceconductance isG(ε)=where ε=(E−ER)/(Γ/2),Gdrepresents non-resonance conductance,ERand Γ are positions and widths of resonance peaks, respectively[40]. The antisymmetric factorqcharacterizes the coupling strength between the continuous and the bound states. Whenq>0, valley is on the lefthand side of the asymmetric formant; while in the case ofq<0, valley is on the right-hand side of the asymmetric formant. So, the first resonance peak has an antisymmetric factorq>0 while the second resonance peak has an antisymmetric factorq<0,as shown in Fig. 2(a).

Besides, the position of Fano-type resonance peak is also related to the frequency of oscillating field and the depth and width of static potential well.The relationship between conductance and incident energy at different frequency oscillation fields is depicted in Fig. 2(b). Comparative analysis of these results shows that the asymmetric resonance peak moves towards a higher energy direction along with the increase in frequency. From Fig. 2(c), we can analyze that the position of common vibration peak moves towards the low energy direction along with the increase in depth of the static potential well. The reason behind this is the lower bound energy level which is due to the increase in depth of the static potential well. As shown in Fig. 2(d), as the width of the static potential well increases, the position of the resonance peak moves towards the left-hand side.

The change in conductance occurs as the distance between two potential wells increases as shown in Fig. 3. It is found that as the distance between the two quantum wells increases, the position of first resonance peak moves towards the righthand side. However, the position of the second resonance peak moves towards the left-hand side. In the case of our double-well potential structure, when the two externally oscillating fields have different phases, the time inversion symmetry of the system breaks. In this case, Fano’s antisymmetric factorqbecomes complex[40]and its formula can be expressedThe asymmetric and symmetric formant is due to|Imq|a nd | Req|≪|Imq|, respectively. In the case of asymmetric linear patterns, the valleys of left and right-hand sides of the asymmetric peak correspond to Req>0 and Req<0, respectively. Therefore,the relative phase of the two oscillating fields can change the shape of Fano-type formant[12].

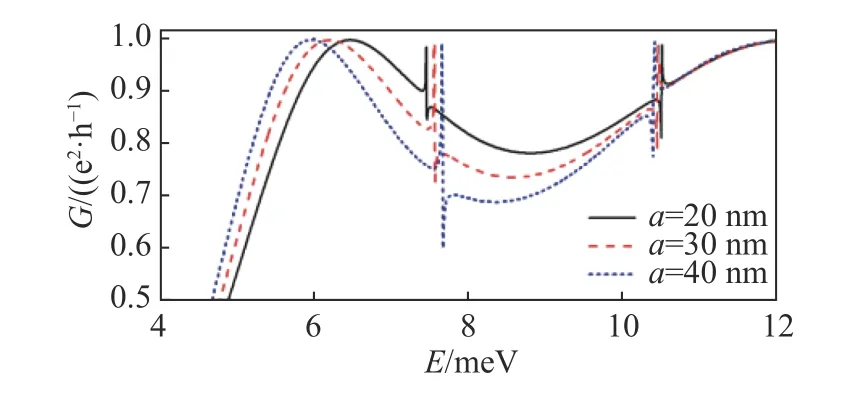
Fig. 3 Conductance G as a function of E for different separation distance between two quantum wells at α=β=0, ky=0.006 nm−1 , ћω =11 meV , V1=1.0 meV,V0=−50 meV and d =200 nm.

The variation in phase-dependent conductance is shown in Fig. 4.Fig. 4 Variation of Fano-type resonance line-shape in conductanceGwith β at α=0,a=40 nm,ky=0.006 nm−1, ћω =11 meV,V1=1.0 meV,V0=−50 meV andd=200 nm. (a) β= 0; (b)(d) β=π.

If we consider α=0 , then β represents the relative phase of the two oscillating fields. Analysis of this figure led us to conclude that the asymmetric peaks and valleys change along with the change in relative phase. When β changes from 0 to π, the valley of the first asymmetric formant moves from the right-hand side to the left-hand side. While the second one moves from the left-hand side to the right-hand side. Moreover, in the case of critical phase 3π/11, the asymmetric peak becomes a symmetrical resonance peak. For relative phase in interval ( 0,3π/11), R eq>0 , while in interval ( 3π/11,π),Req<0 . In fact, the critical relative phase3π/11 corresponds to Req→0 (but Imq≠0), where the symmetric resonance peak appears.

4 Summary

In this paper, we use Floquet scattering matrix theory for the investigation of resonant tunneling of Dirac electrons in the graphene time-periodic double-well potential. The interaction between Dirac electrons and oscillating field produces photo-assisted resonant tunneling. This tunneling is responsible for the production of sharp asymmetric Fanotype resonance peaks. The asymmetric Fano-type resonance originates from the quantum interference between the bound and continuous states. Our numerical data for double-well potential led us to conclude that the Fano-type resonance spectrum split into two asymmetrical resonance peaks with different lines. In addition, the relative phase of two oscillating fields can also change the line shape of the asymmetric Fano-type resonance peak. When the relative phase increases from 0 to π, the valley of the resonance peak moves from one side of the peak to the other. At critical phase 3π/11, the asymmetric resonance peak becomes symmetrical. Moreover,the frequency and amplitude of the oscillating field,as well as the structure of the static potential well,can be used to modulate the resonance peak. Finally,we suggest that these properties can modulate the electronic transport properties of Dirac in graphene.