定向分布于两圆上的两点间距离最值的探求

李金兴

(浙江省萧山中学 311201)

1 两点连线段与两圆心连线段垂直时

为便于阐明探求方法,先举一个简单的例子.

例1已知点P在圆C1:x2+y2=1上,点Q在圆C2:(x-2)2+y2=4上,且PQ⊥x轴,求P,Q两点间距离的最大值.

分析当两圆相交时,P,Q两点间距离的最小值为0，故不予研究.为求P,Q两点间距离的最大值,由对称性不妨设P在x轴上方、Q在x轴下方(如图1).

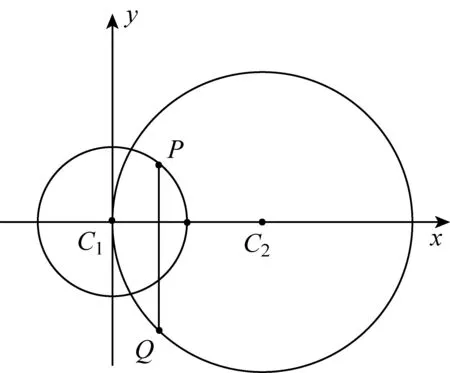
图1

图2

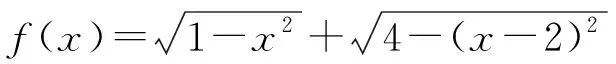
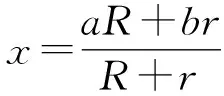
2 两点连线段与两圆心连线段不垂直时

为便于阐明探求方法,仍先举一个简单的例子.

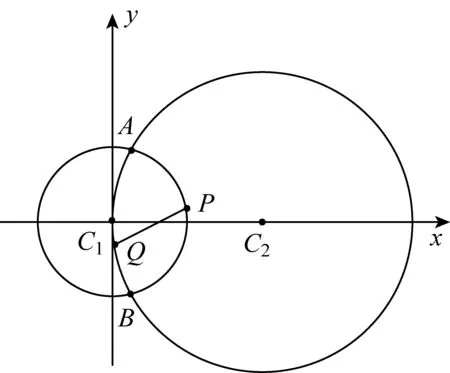
图3

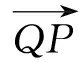
将直线PQ与C1的方程联立消去y得

而将直线PQ与C2的方程联立消去y得

所以

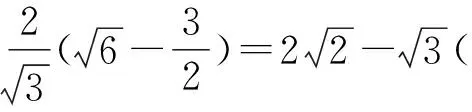
小结改变直线PQ的倾斜角，可以用同样方法构造向量数量积来求P,Q两点间距离的最大值.事实上，适当旋转坐标系可以更直观地来解决该问题，请看例2另解如下：

图4

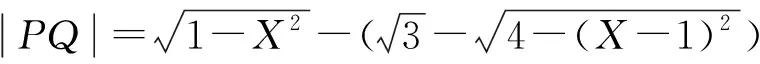
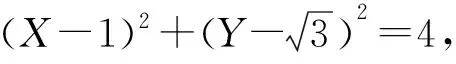
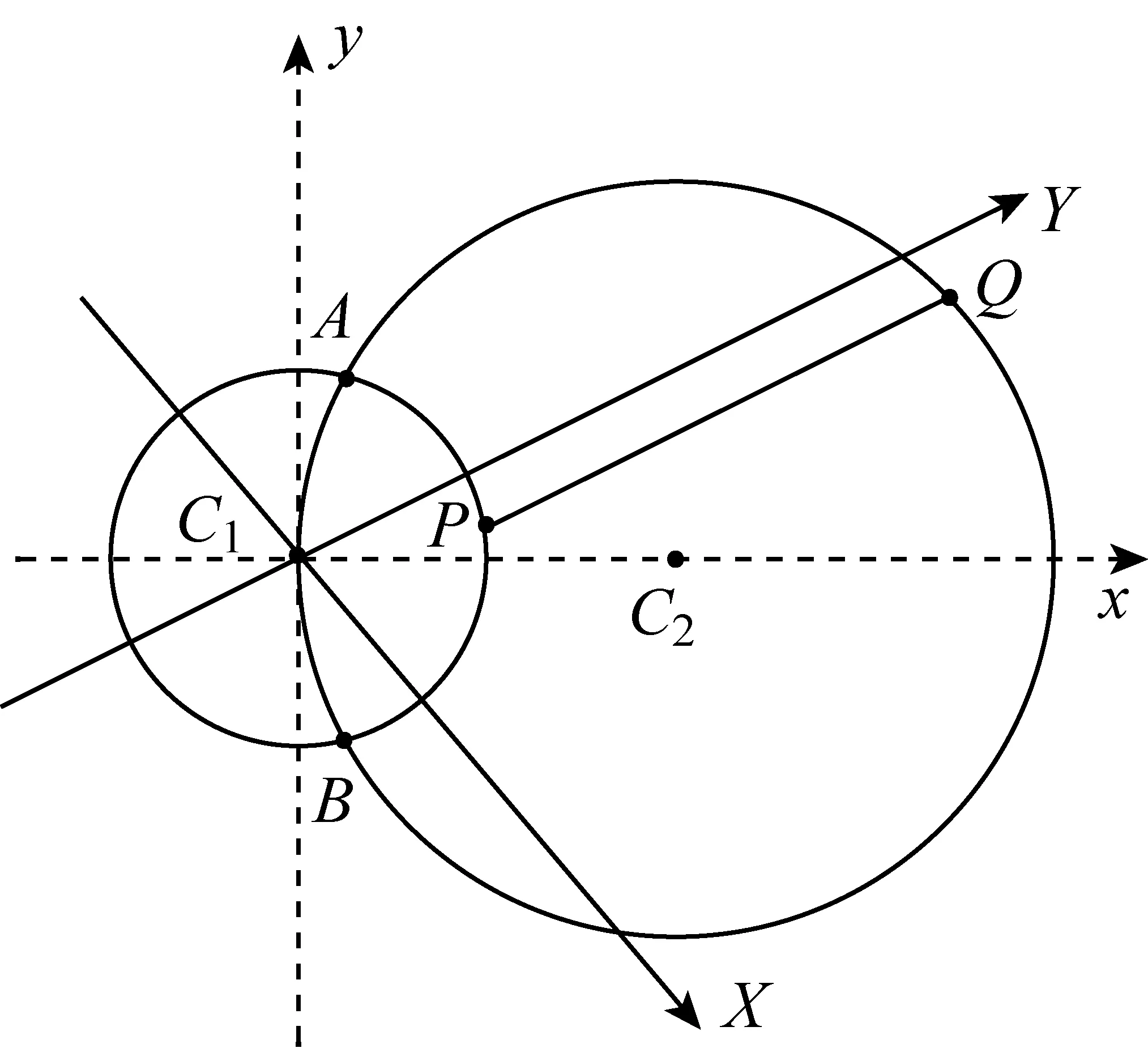
图5

(1)若P在圆C1的上半圆上，则

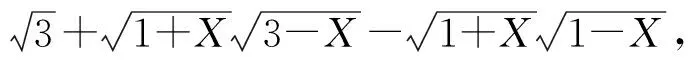
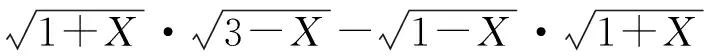
消去X,Y得

再与X2+Y2=1联立解得

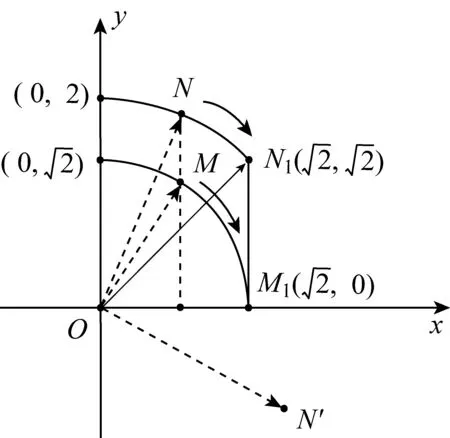
图6

(2)若P在圆C1的下半圆上，则

3 两圆处于不同位置关系时的应用举例

上述三个例子中给出构造向量、并利用向量的数量积或叉积的几何意义来求定向分布于两圆上的两点间距离的最值；对于不同位置关系的两圆，需要合理选择方法.

例4已知点P在圆C1:x2+y2=1上，点Q在圆C2:(x-4)2+y2=4上，且直线PQ的倾斜角为30°，求P,Q两点间距离的取值范围.

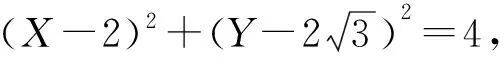
图7

(2)若P在下半圆上、Q在上半圆上的情形；此时，P,Q两点间距离

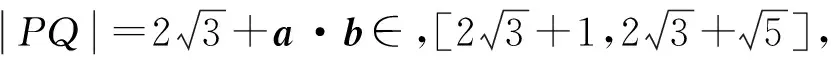
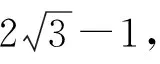
例5已知点P在圆C1:x2+y2=1上，点Q在圆C2:(x-2)2+y2=16上，且直线PQ的倾斜角为30°，求P,Q两点间距离的取值范围.

图8

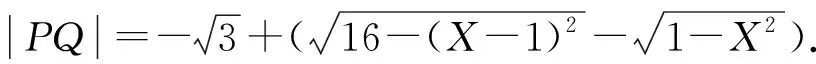
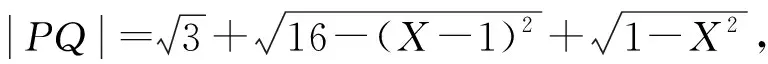
(4)若P在上半圆上、Q在下半圆上；则P,Q两点间距离

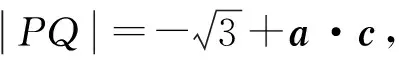
综上所述，P,Q两点间距离的取值范围为

反思例5的解答中构造向量数量积时由于两个向量的旋转方向相反，利用图形直观容易求得数量积的最值，但构造向量叉积时由于两个向量的旋转方向相同，有时不能利用图形直观来求叉积的最值.