“三角形分类”中的化解疑问教学

□张红勤 张小燕

对三角形进行分类是进一步认识三角形的方法。三角形按角的特征可以分为直角三角形、钝角三角形和锐角三角形；按边的特征可以分为等腰三角形（包括等边三角形）和不等腰三角形。人教版教材通过安排学生操作，在按角分类中认识直角三角形、钝角三角形和锐角三角形的特征和名称，并用集合图对这3类三角形进行表征。认识等边三角形和等腰三角形则通过观察边的特征来实现。

分析发现，教材只给出了这些三角形的名称，而没有给出其定义。不过在实际教学中，教师一般会对按角分类的3种三角形给出“口头定义”，如“有1个角是直角的三角形叫作直角三角形”。那么，学生对于按角分类得到的3种三角形的名称以及这样的“口头定义”会有疑问吗？课题组开展了本次化解疑问教学的实践研究。

一、问卷设计与意图解读

问卷只针对按角分类的三角形进行调查，分为3个板块。

第一板块：

三角形有3个角，有3条边。给三角形分类，可以按角的特征分，也可以按边的特征分。如果按角的特征对三角形进行分类，可以根据三角形的3个角分别是什么角来分。

图1中有7个三角形，按角分类，可以分成3类。第一类：②⑦，3个角，1个是直角，2个是锐角，这类三角形叫作直角三角形。第二类：③⑥，3个角，1个是钝角，2个是锐角，这类三角形叫作钝角三角形。第三类：①④⑤，3个角，都是锐角，这类三角形叫作锐角三角形。

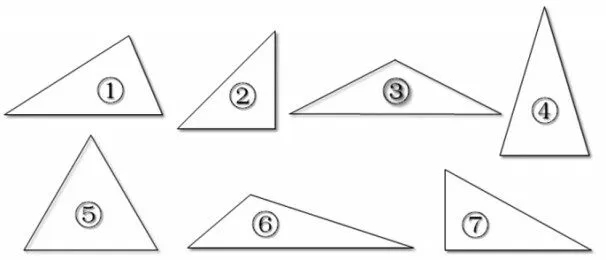
图1

第二板块：

直角三角形、钝角三角形、锐角三角形是这3类三角形的名称，《数学辞海》中是这样定义它们的：直角三角形指有1个角是直角的三角形；钝角三角形指有1个角是钝角的三角形；锐角三角形指3个角是锐角的三角形。

第三板块：

当你仔细阅读完上面关于“三角形的分类”的材料之后，心中有什么疑问吗？想一想，把你的疑问大胆地写下来吧！

问卷首先呈现7个三角形，接着将7个三角形按角的特征分成3类，详细介绍了每类三角形的特征和名称，这与一般的教学流程一致，目的是让学生清晰地认识这3类三角形，然后给出《数学辞海》中对这3类三角形的数学定义，目的是让学生认识到这样的定义是规范科学的，最后让学生在对上述内容进行阅读和思考的基础上，写下自己内心的疑问，目的是看看学生对这样的分类、取名、定义会存在什么疑问。

二、测试分析与疑问确定

（一）测试分析

测试在2个班级共81名学生中展开，通过对学生写下的疑问进行分类归并，去掉与本节课内容无关的疑问，发现学生对三角形按角分类的疑问主要有以下3种。

（1）对3类三角形的名称存在疑问。有19人提出了此种疑问，占测试总人数的23.5%。典型表述如下：

（2）对3类三角形的定义存在疑问。有11人提出了此种疑问，占测试总人数的13.6%。典型表述如下：

（3）对三角形的类别存在疑问。有23人提出了此种疑问，占测试总人数的28.4%。典型表述如下：

（二）疑问确定

深入分析上述3种不同指向的学生疑问后不难发现，这些疑问虽看上去不一样，但疑问的本质是一致的。如“直角三角形有2个锐角，为什么不叫锐角三角形”，学生是从角的类型的数量上考虑三角形的名称，其实就是对三角形角的本质属性存在疑问；又如“为什么直角和钝角只要1个就好了，锐角却要3个”“有没有1个角是锐角，1个角是直角，1个角是钝角的三角形呢”，同样是学生对三角形角的本质属性存在疑问。

看来，仅通过按角分类得出3类三角形的名称及定义，学生对这样获得的数学结论是存在疑问的。因此，在“三角形分类”的教学中，可将“三角形按角分类为什么这样取名和定义”确定为学生疑问。

三、疑问分析与“化疑”实施

（一）疑问分析

1.教学价值分析

三角形的3个角有3种情况：3个锐角，1个直角+2个锐角，1个钝角+2个锐角。也就是说，任何一个三角形至少有2个锐角。可见，仅从数量上讲，有2个锐角是三角形的共同属性，而非某一个三角形的本质属性。因此，有1个直角、有1个钝角才是这类三角形的本质属性，故用直角三角形、钝角三角形取名及定义时只讲1个直角、1个钝角，是抓住了这类三角形的本质属性，是科学的、简洁的。当然，锐角三角形则必须说全3个锐角。也有这样的方法，可以用三角形中的最大角来取名，如最大角是直角就是直角三角形，不难发现，这其实也是抓住了一个三角形中最多只有1个直角这一本质属性，当最大角是锐角时，即3个角都是锐角。

那么，学生为什么会对按角分类的取名和定义有疑问呢？这是因为，学生刚开始认识这3类三角形时，对三角形3个角的各种组合是不明白的，即对三角形角的本质属性不了解。因此，学生会认为要说全3个角分别是什么角才能把这个三角形的特征说清楚。由此，就造成学生对3类三角形的取名和定义心存疑问，甚至认为还有别的三角形。

显然，在探究“为什么直角和钝角只要1个就好了，锐角却要3个”这样的疑问时，自然会触及三角形角的本质属性。正视学生的这些疑问，在学生的疑问处开展教学，直击按角分类的3类三角形的本质属性，实现更为深刻的理解。

2.可行性分析

也许有教师会想，当学生学过三角形的内角和是180°之后，自然能清楚一个三角形中最多只能有1个直角或1个钝角。但“三角形内角和”教学中牵连的这个问题，更多指向对180°的运用，而非对三角形角的本质属性的解读，因此对于化解学生疑问而言，效果会不明显。特别是，即使学生没有学过三角形的内角和是180°，化解“三角形按角分类为什么这样取名和定义”这个疑问也是可行的，即可以让学生通过画图的方式，借助几何直观理解各种三角形3个角的特征，进而认识三角形角的本质属性。而且，这样的操作活动正是学生在头脑中构建三角形的过程，是培养空间观念的好时机和好手段。

由此，形成化解这个疑问的设想：先让学生按角的特征对7个三角形进行分类，然后观察并描述3类三角形的特征并取名，接着呈现3类三角形的定义，引发学生认知冲突，暴露学生的疑问，最后进行探究化解。

（二）“化疑”实施

课始教师板书“三角形的分类”。通过讨论，学生知道三角形可以按角或边的特征分类。在明确先按角分类后，教师为每位学生提供7个三角形，学生得出两种分类情况，一是按有无直角分为2类，二是按有直角、有钝角、都是锐角分成3类。对两种分法作肯定反馈之后，师生讨论认可分成3类更为精确。

师：我们再来看看这3类三角形，它们的角到底有什么特征呀？

（根据学生回答，板书：1个直角、2个锐角；1个钝角、2个锐角；3个锐角）

师：分类完成了，如果要给这3类三角形取个名称，你会怎么取名呢？

生：1个直角、2个锐角的三角形叫直角三角形；1个钝角、2个锐角的三角形叫钝角三角形；3个角都是锐角的三角形叫锐角三角形。

（学生认可这样的名称，教师对应板书）

师：现在，你们知道什么叫直角三角形、钝角三角形和锐角三角形了吗？

（同桌先互相说一说，然后教师请一名学生回答。学生在说3类三角形的意义时，都是把3个角说完整的）

师：同学们，语文学习中我们要想知道对一个词语解释得好不好，可以查一查辞典。在数学中，我们也可以查！

（教师PPT出示《数学辞海》封面，之后出示直角三角形、钝角三角形和锐角三角形的定义，如图2，学生齐读）

图2

师：同学们，读了《数学辞海》中的定义，再看看黑板上我们刚才的研究，现在你心里有什么疑问吗？

（一开始举手的学生不多，只一会儿，就有近一半的学生举手了）

生：为什么直角三角形和钝角三角形只说1个角，而锐角三角形却要说3个角？

师：呀，真的，好奇怪！哪些同学心里也有这个疑问？

（一半以上的学生举手了）

师：再思考一下，你心里还有什么疑问吗？

生：直角三角形有2个锐角，比1个直角多1个，为什么叫直角三角形而不叫锐角三角形呢？

师：呀，也好奇怪，明明锐角数量多，为什么却用数量少的直角取名？

生：除了这3类，还有没有其他的三角形？

师：哦，我们只研究了7个三角形，世界上有无数个三角形，还有别的三角形吗？你真会思考。

师：大家有这么多疑问，这可怎么办？怎么解决呢？要不，你们自己先选一个疑问，然后想办法解决！老师建议你们可以在白纸上画一画，在小组里讨论讨论。

（学生尝试在纸上画一画，同桌进行交流，然后反馈）

生：我知道了，一个三角形中不可能有2个直角，只能有1个直角，另外2个角一定是锐角，所以《数学辞海》里只讲1个直角。

师：什么意思？我没听懂。你们听懂了吗？

（教师请学生在实物展台上边演示边解释，如图3）

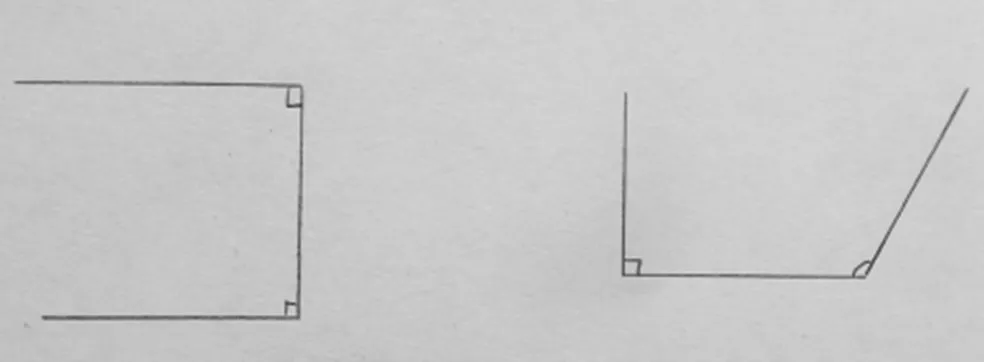
图3

师：我现在听懂了，你们呢？

生：就是说1个三角形中不可能有2个直角，如果有2个直角，就组不成三角形了。

生：我也画了，有1个直角，另外2个角一定是锐角。

生：更不可能有1个直角和1个钝角。

生：可以有1个钝角。如果有1个钝角，另外2个肯定是锐角。

师：原来如此！现在你们明白《数学辞海》为什么这样定义直角三角形和钝角三角形了吗？同桌互相交流一下。

生：只要讲1个直角或1个钝角就够了，另外2个角一定是锐角，讲都不用讲。

师：哦，直角和钝角才是直角三角形和钝角三角形真正的特征，锐角不是。现在我真正明白了。不过，2个锐角其实讲了也可以，就是有点什么感觉？

生：啰唆。

师：那么锐角三角形呢？

生：锐角三角形只说1个锐角不行，它有可能是直角三角形，也有可能是钝角三角形。

（学生纷纷表示赞同）

师：为什么呀？

生：因为直角三角形和钝角三角形都有2个锐角，你只讲1个锐角，就不能确定了。

生：我发现三角形至少有2个锐角，所以锐角三角形必须要把3个锐角都说出来才知道。

师：同学们，研究到现在，这些疑问你觉得解决了吗？

生：我觉得为什么叫直角三角形和钝角三角形我已经明白了，因为虽然2个锐角数量上多，但直角和钝角才是特征。

生：《数学辞海》中为什么这样定义我也明白了。

师：看来前面两个疑问我们都解决了。那么，除了这3类三角形，还有其他类型的三角形吗？

（大部分学生认为没有了，也有少数学生认为有）

师：不管有没有，讲理由。

生：我都画过了，没有了。

生：刚才不是说了嘛，最多只能有1个直角或1个钝角，那就不可能再有别的三角形了。

师：确实，三角形按角分类，只有这3类。

（几何画板演示：拖动三角形的1个点，不管怎么动，都是黑板上这3类三角形中的1种）

师：所以，三角形按角分，可以分成3类，直角三角形、钝角三角形和锐角三角形。

（教师用集合图表征这3类三角形，略）

……

教学至此，本课化解疑问的教学已经完成。后续接着研究按边的特征分类以及完成一些相应的练习。