基于交织序列的偏振方向映射方法

王 霞，苏子航，赵家碧，徐 超，金伟其

（北京理工大学 光电学院 光电成像技术与系统教育部重点实验室，北京 100081）

引言

偏振成像技术是在获取目标偏振信息的基础上利用所得到的信息进行目标重构增强的过程，相较于强度成像，偏振成像技术可以提供更多维的目标信息[1]。偏振方向作为光场偏振态的一个重要构成因素，在对场景信息的解译上有着重要的作用[2-3]。

线偏振成像技术中，偏振方向本质上是一条直线的方向，而直线方向是用其法向量表示，因此偏振方向本质上是一个二维信息。在偏振态的斯托克斯矢量表示方法[4]中，以2个分量综合信息表示偏振方向；目前较多使用的偏振方向表示方法是偏振角，其以一维数据的形式去表示偏振方向，但由于存在着数值突变，这些数值突变并不反映任何真实的物理信息[5]，在实际使用中一般会引入较高的噪声。因此，传统的偏振方向表示方法存在以下问题：1）映射结果信息维度具有较高信息维度；2）一维信息映射方法本身缺陷引起的对噪声鲁棒性低。

对于信息维度问题，信息降维方法有利用线性特征提取的主成分分析（PCA）、独立成分分析（ICA）等方法，也有多用于高光谱图像信息降维中的等距映射（ISOMAP）、局部线性嵌入（LLE）等方法[6]，但这些方法是基于图像统计数据的降维方法，不同的源图像中相同的物理信息在映射结果中也会不同，不是一般性物理量之间的映射规则。在这些映射方法中，具有距离保持特性的映射方法可以保存数据之间的距离和局部拓扑信息，可以有效提高数据挖掘步骤的性能[7]。

对于噪声问题，文献[8]分析了偏振测量次数、噪声类型与偏振角偏振度精度之间的关系；文献[9]分析了偏振角色散函数与噪声之间的关系。目前的研究中，缺少由于偏振方向映射方法本身缺陷带来的噪声的相关分析。

本文第1节中基于交织序列的方法提出了一种将偏振方向映射为一维数据的映射方法。第2节中首先研究了距离保持特性与映射方法噪声鲁棒性的关系，之后分析了本文提出的映射方法的距离保持特性及其噪声鲁棒性。第3节进行了仿真实验与实际场景实验，结果证明本文所提出的映射方法具有较好的噪声鲁棒性。

1 基于交织序列方法的偏振方向一维数据映射

部分偏振光是同方向传播的自然光和完全偏振光互相叠加后生成的光[4]，如图1所示，在坐标系XOY中，自然光部分的强度为IN，完全线偏振光的强度为IP，偏振方向为代表完全线偏振光线振幅方向的橙色直线LP的方向。由于偏振角与偏振方向之间存在一一对应的关系，因此本文中仍采用偏振角来表示几何关系。图1中偏振方向的偏振角θ为Y轴右侧部分的直线LP与X轴正方向的夹角，

图1 部分线偏振光成分Fig.1 Components of partial linear polarized light

斯托克斯矢量由4个分量S0、S1、S2、S3组成，其中S1、S2包含了偏振的方向与线偏振强度信息。结合图1中的所示参量，斯托克斯矢量的表达如（1）式所示：

将S1、S2中 的线偏振强度IP提取出来，可以以二维数据 ( cos2θ,sin2θ)的形式表示偏振方向。

为将二维数据映射下的偏振方向映射为一维数据，本文采用交织序列的映射方法[10]。交织序列通过“洗牌”的方式融合2个序列，其定义为：对于集合S中的2个序列 (xi) 和 (yi)，i=0,1,2,···，其交织序列 (zi) 为x0,y0,x1,y1,···，如（2）式所示：

对于元素x,y∈(0,Bn)的二维数据，首先将其B进制形式按位分离成2个长度为n的序列，其次交织2个序列，获得一个长度为 2n的序列，就可以唯一确定另一个属于 的实数，也就是会形成一个二维平面区域向 一维区间的单射映射[11]。

综上，针对偏振方向，首先确定序列进制B与序列长度n，再通过以下4个步骤将其转化为一维数据。

1）偏振方向的二维数据映射：将偏振方向映射为二维数据( cos2θ,sin2θ)；

2）二维数据归一化：对于二维数据 (X,Y)，通过(3)式归一化为平面区域 (0,Bn)×(0,Bn)内的数据(x,y)；

3）归一化数据序列化：归一化数据 (x,y)对应的序列 (xi) 和 (yi)是x、y在B进制下按位分离的结果，如（4）式所示；

4）交织序列编码：求 (xi) 和 (yi)的交织序列(zi) 并 转换为数值量z，如（5）式所示，即为映射结果。

交织序列将二维数值映射为一维数值，且在二维空间分布上具有处处不连续，即存在数值跳变。

对于交织序列 (zi)1和 (zi)2，当其关系为（6）式所示的情况时，这2个序列空间位置相邻且出现最大数值跳变：

按位相减得到最大跳变值并归一化：

从（7）式可知，跳变值与n无关，与B成反比，当B足够大时，在离散数据处理方法中，可认为该映射在平面空间中是连续的。

在极坐标系中，将圆中每个点的角坐标θ转化(cos2θ,sin2θ)的二维数据，再按上述步骤，在不同进制B下进行交织序列映射，映射结果如图2所示。可以看出，当B=30时，可以认为灰度分布是连续的。

图2 不同B值下交织序列映射法对极坐标角度坐标映射结果Fig.2 Mapping results of polar -coordinate angle coordinates by mapping method of interleaved sequence under different B values

2 偏振方向映射方法的距离保持特性研究

2.1 距离保持特性对映射方法噪声鲁棒性的影响

当映射X→Y中存在较大的数值突变现象时，如图3所示，如果自变量x2受到噪声污染，沿不同的变化方向变为x1、x3， 其映射结果为y1、y3，对应的噪声为 ∆y12、∆y32， 显然有 ∆y12≫∆y32。因此，相较于存在较大数值突变的映射关系，非突变或者突变数值较小的映射关系会在因变量中引入更少的噪声，即对噪声有较好的鲁棒性。

图3 映射中数值突变对因变量噪声的影响Fig.3 Influence of numerical mutation in mapping on noise of dependent variable

对于一个映射关系，该映射关系中“突变”现象存在的程度可以用距离保持特性来表示。距离保持特性的定义为：在映射关系中，定义域内自变量之间的“距离”与值域中对应因变量之间的“距离”的相似程度[6]。根据其定义，如果映射关系存在较好的距离保持特性，对于任意一个基准y0=f(x0)，则都存在如（8）式所示的关系：

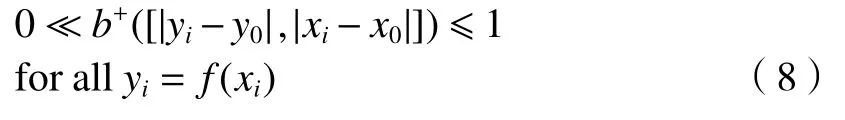
式中：b+([ai,bi])forallai,bi表示a、b之间的正相关系数，（8）式表示了“距离”之间的正相关系数应尽量接近于1，即应具有尽量好的正相关性。

如果一个映射关系是非突变或者突变数值较小的映射关系，则对任意一个基准y0=f(x0)，都存在如（9）式所示的关系：

式中：ε为一个不大的阈值系数。

满足（8）式表示映射关系f具有较好的距离保持特性，满足（9）式表示映射关系f具有小的数值突变，即噪声鲁棒性较好。（8）式是（9）式的充分条件，即满足式（8）条件的映射关系是一个非突变或突变数值较小的映射关系。

综上所述，如果一个映射关系满足（8）式，那么该映射关系对噪声有着较好的鲁棒性。

2.2 偏振方向映射方法距离保持特性的评价方法

对于要素A，使用方向距离表示其自变量之间的“距离”。如图4所示，对于2个偏振方向LP1、LP2的方向之间的距离，以2条相交直线的锐角夹角为参数，定义2条直线的方向距离（direction distance，DD），如（10）式所示，

图4 两偏振方向之间位置关系Fig.4 Position relationship between two polarization directions

式中： ∆θ=|θ1−θ2|；δ 为 直线LP1、LP2的夹角。方向距离为0时2直线重合，方向距离为1时2条直线垂直。

从（8）式可以看出，评价一个映射方法的距离保持特性需要确定3个要素：A）自变量之间的“距离”；B）因变量之间的“距离”；C）相关性检验方法。

对于要素B，因为映射结果是数值，所以因变量之间的“距离”D使用因变量之间的欧式距离表示，如（11）式所示：

式中：yi、yj为 2个因变量； ∥ ·∥2代表取二范数。

对于要素C，（8）式中关注的重点是2个变量之间的相关性，而不是线性关系，因此本文中使用更关注变量间单调关系的Spearman相关系数作为相关性度量。Spearman系数的取值范围为−1～1之间，系数越大，则相关性越强[12]。

根据上述内容，对传统的偏振角映射方法（AoP mapping）与本文提出的基于交织序列的偏振方向映射方法（Sequence-Interleaving mapping）进行距离保持特性评价，结果如图5所示。可以看出，本文所提出的映射方法满足（8）式，而偏振角映射方法则不满足，因此本文所提映射方法相较于偏振角映射方法具有较好的噪声鲁棒性。

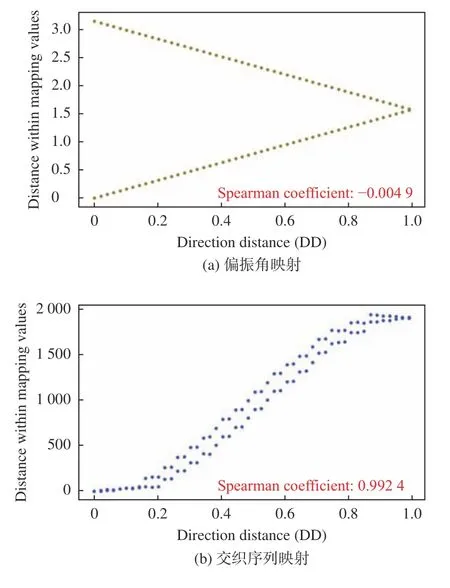
图5 方向距离与映射关系中因变量距离之间的相关性Fig.5 Correlation of direction distance and dependent variable distance in mapping relationship

3 实验

本文实验分为仿真实验与真实场景实验2部分。

3.1 仿真实验

在仿真实验中，模拟视场中存在一个表面光滑的球体，自然光光线均匀照射在球面与背景上，设定照明自然光光强，球体折射率与空气折射率，根据菲涅耳公式可以计算得到模拟球面上每一点的偏振态；其次模拟线偏振成像过程获取球面成像数据并添加指定信噪比（SNR）的高斯噪声；最后利用不同的偏振方向映射方法得到噪声污染后的偏振方向映射结果，并以未被噪声污染的映射结果为真值计算峰值信噪比（PSNR），仿真结果如图6、表1所示。

图6为当原始图像被高斯噪声污染成不同SNR的图像时，与对应仿真映射结果的PSNR值的关系。可以看出，当SNR<3.2时，两种映射结果的PSNR基本一致，因为此时信号已几乎被噪声淹没，因此映射方法本身对噪声的鲁棒性对映射结果的噪声水平几乎不会产生影响；当SNR>3.2时，本文所提方法映射结果的PSNR较高，对噪声具有较好的鲁棒性，平均PSNR提升为6%。表1展示了当SNR=20时的仿真结果及其真值图像。从图中可以看出，相较于偏振角映射方法，本文所提映射方法在某些角度位置上噪声较小，从而使对应的峰值信噪比得到提升。

图6 交织映射方法及传统AoP映射方法下映射结果PSNR与加入不同高斯噪声后图像SNR之间的关系Fig.6 Relationship between SNR of image after adding different Gaussian noises and PSNR of mapping results under interleaved mapping method and conventional AoP mapping method

表1 加入噪声SNR=20时偏振角映射方法与交织序列映射方法映射结果及其PSNRTable 1 Mapping results and PSNR values of mapping methods of polarization angle and interleaved sequence when SNR is 20

3.2 真实场景实验

在真实场景实验中，本文采用LUCID VISION LABS的PHX050S可见光分焦平面偏振相机，首先对场景进行成像数据采集实验，再结合分焦平面图像标定校正与瞬时视场误差校正方法[13]解算得到场景的Stokes矢量，最后分别使用偏振角映射与基于交织序列的映射方法得到映射结果，如图7所示。

可以看出，绿框中球体的实验结果与仿真实验一致，图7（c）中因数值突变而出现较多的噪点；相较于图7（c）中左侧红框箱子表面灰度分布杂乱程度，图7（d）中的杂乱程度明显减低，也即是噪声水平明显降低。

图7 实验结果Fig.7 Experimental results

在解算结果的基础上，本文进一步采用偏振图像融合技术中的非负矩阵分解偏振特征提取方法NMF[14]分别对3个映射方法下的实验结果进行特征提取，每个映射方法下会提取出3个偏振特征图像F1、F2、F3，之后使用无参考的信噪比评价模型NPPSNR[15]检测偏振特征的噪声水平，结果如表2所示。从表2可知，无论是从同类偏振特征的噪声水平或者是噪声水平的均值上比较，平均NRPSNR提升了约14%，本文所提的偏振方向映射方法对噪声具有较好的鲁棒性，在偏振特征提取时可以减少噪声的引入，进而有利于偏振融合、探测等工作的数据处理。

表2 场景偏振特征噪声水平Table 2 Noise measurement of polarization features of scenes

4 结论

本文针对偏振方向的映射方法中存在的可视化程度低、信息复杂度高或由于距离保持特性差造成的对噪声鲁棒性低的问题，提出了基于交织序列的具有距离保持特性的偏振方向映射方法，实验结果表明：

1）本文提出的映射方法具有较好的可视化特性与较低的信息复杂度。所提出的偏振方向映射方法可将二维的偏振方向转化为一维数据，相较于斯托克斯矢量表示法，可直接将偏振方向转化为像素灰度数值，降低了信息的维度。

2）本文提出的映射方法具有更好的距离保持特性。该映射方法的映射值域与映射源之间具有良好的距离保持特性及更好的噪声鲁棒性。相较于传统的偏振角映射方法，在偏振角范围分布较广而使用偏振角映射方法存在数据突变问题时，可以有效解决映射结果不能真实反映映射源的问题，从而减少噪声的引入，有利于提升偏振融合、探测的效果。