功能MRI时间分辨率对基于格兰杰因果模型的脑效应连接的影响

张欣欣，杨青青，于春水,2，梁 猛*

(1.天津医科大学医学影像学院，天津 300203；2.天津医科大学总医院医学影像科，天津 300052)

格兰杰因果关系分析(Granger causality analysis，GCA)是揭示脑区间效应连接(effective connectivity，EC)的强有力工具，已广泛用于功能MRI(functional MRI，fMRI)研究[1-5]。利用GCA推断因果性的基本原理如下：若脑区X的时间序列在过去时刻的值对预测脑区Y的时间序列当前时刻的值有显著贡献，则认为脑区X的功能活动为因，Y则为果。因此，fMRI数据的时间分辨率可能是检测脑区间EC的潜在制约因素[6-7]。既往研究[6，8]基于仿真数据提出较高时间分辨率可提升GCA结果的稳定性和敏感性。目前fMRI数据最常用的重复时间(repetition time，TR)多为2～3 s。多层同步采集序列[9]的出现，将全脑fMRI采集时间缩短至亚秒级，而这是否会对GCA结果产生显著影响目前尚不得而知。本研究观察fMRI时间分辨率对基于GCA模型的脑EC的影响。

1 资料与方法

1.1 数据来源 基于人类大脑连接组计划(https://neuroscienceblueprint.nih.gov/human-connectome/connectome-programs)，于公开数据库随机抽取40名健康受试者，男20名，女20名，年龄30～37岁，平均(34.3±1.1)岁。纳入标准：右利手，无神经或精神疾病史[10]。

1.2 数据预处理 采用梯度回波-回波平面成像(gradient echo-echo planar imaging，GRE-EPI)序列采集颅脑静息态fMRI(resting-state fMRI，rs-fMRI)数据，TE 33.1 ms，TR 720 ms，FOV 208 mm×180 mm，矩阵104×90，平面分辨率2 mm×2 mm，FA 52°，层厚2 mm，层数72，带宽2 290 Hz/Pixel，共采集1 200个时间点数据，采集时间14.4 min。采用Matlab R2013b和DPARSF软件行图像预处理，包括梯度失真校正、头动校正、EPI图像失真校正、空间配准、去除线性漂移、回归协变量和样条插值及带通滤波(0.01～0.08 Hz)，见图1。

图1 受试者女，36岁 A～C.分别为预处理后脑部冠状位、矢状位及轴位fMRI数据图

1.3 fMRI数据下采样 为保证数据一致性，于上述预处理后，经时间下采样生成采集不同时间分辨率的fMRI数据。最高时间分辨率(TR 0.72 s)数据为上述预处理后共1 200个时间点的fMRI数据；中等时间分辨率(TR 1.44 s)数据为上述数据经2倍下采样获得，取奇数时间点，共600个时间点；最低时间分辨率(TR 2.16 s)数据为最高分辨率数据经3倍下采样获得，共400个时间点。

1.4 GCA分析 基于人类脑网络组图谱(http://atlas.brainnetome.org)[11]将大脑分为246个脑区，以每个脑区所有体素的fMRI时间序列的均值作为该脑区的平均时间序列。以Matlab和REST软件(http://restfmri.net/forum)对所有脑区平均时间序列行两两间GCA。采用基于残差的GCA分析方法，假设X、Y分别为2个脑区的时间序列，以下列公式计算脑区间的GCA关系：

(1)

var(μt)=R2

(2)

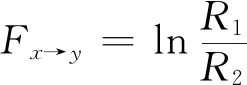
(3)

(4)

var(μ′t)=T2

(5)

(6)

公式(1)为自回归模型，代表利用Y脑区过去时刻的神经活动信息预测其现在时刻神经活动的模型，其中p为模型阶数(即使用过去p个时间点的信息)，Mi为回归系数，εt为残差，残差方差即为R1。公式(2)表示在公式(1)基础上进一步增加X脑区过去时刻的神经活动信息，以共同预测Y脑区现在时刻的神经活动，模型残差μt的方差记为R2。利用公式(3)可基于R1和R2计算X脑区对Y脑区的效应连接Fx→y。若X脑区过去时刻的神经活动信息对Y脑区现在时刻神经活动具有预测能力，即R20，表示X脑区是Y脑区的格兰杰原因；反之，R2≈R1，Fx→y≈0，则X脑区不是Y脑区的格兰杰原因。同理，根据公式(4)～(6)可计算Y脑区对X脑区的效应连接Fy→x。

1.5 统计学分析 采用Matlab R2013b软件，以置换检验及整体错误率多重比较校正方法[12]，分别于个体水平及组水平确定每条EC的统计显著性。确定个体水平统计显著性方法：将所有受试者同一脑区的fMRI信号序列在时间顺序上以相同方式进行随机置换，确保针对同一脑区的置换方式在受试者间一致；针对置换后的fMRI数据重新计算每名受试者所有脑区间的EC；对每名受试者重复上述过程1 000次，每次取全脑最大EC值；1 000个全脑最大EC值构成该受试者的零分布，并将其真实数据所得到的每一条EC值分别与零分布进行比较(针对每条EC值，P值计算为1 000次随机置换中所有大于等于该真实EC值的随机置换所获得EC值所占比例)，即得到每名受试者每条EC经校正后的统计显著性。

确定组水平统计显著性方法：计算每次随机置换后每条连接所有受试者EC的平均值，并获取全脑所有连接的最大平均EC值；1 000次随机置换所得全脑最大EC构成组水平零分布，将其与真实数据所得的每条连接的组水平平均EC值进行比较，即得到每条EC经校正后的组水平统计显著性。校正后P<0.05为有显著统计学意义。

2 结果

组水平不同时间分辨率fMRI数据的GCA结果见图2。模型阶数为1、2、3对应的全脑显著EC条数在TR为2.16 s时分别为792、128及1 504，TR为1.44 s时分别为2 932、1 920及12 500，TR为0.72 s时分别为16 320、43 177及60 204。个体水平上所获结果与上述组水平结果趋势基本一致，见图3。

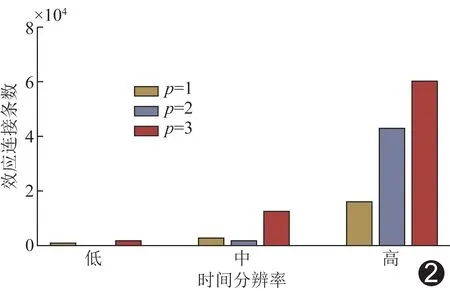
图2 基于不同时间分辨率及模型阶数fMRI数据的组水平GCA结果图

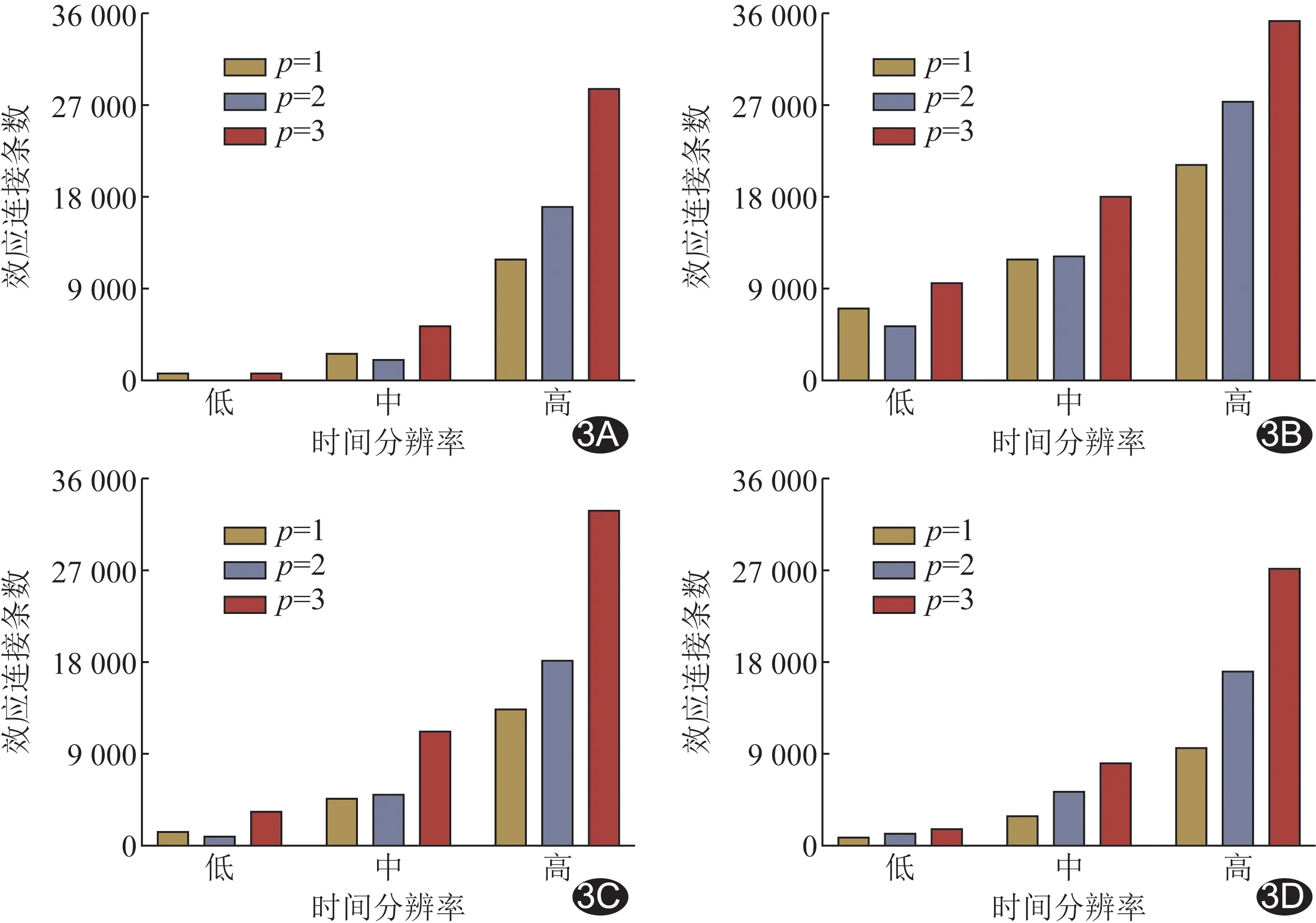
图3 基于不同时间分辨率及模型阶数的fMRI数据的个体水平GCA结果图 A.受试者男，36岁；B.受试者女，34岁；C.受试者女，33岁；D.受试者女，36岁

3 讨论

基于GCA的EC取决于对过去时刻的定义，而模型中过去时刻所包含的具体数据则由单位时间区间内所含数据及过去时刻区间长度共同决定；单位时间区间内所含的数据取决于时间分辨率，而过去时刻区间长度取决于TR(即TR越短，时间分辨率越高)与模型阶数的乘积。

相同时间分辨率条件下，随模型阶数提高，单位时间区间内所含数据不变，但所含过去时刻区间长度增加；虽然检测到的显著EC条数也呈现增多趋势，但不同情况下结果并不完全一致，提示模型阶数增多、即过去时刻区间长度增加并不一定使EC条数显著增加。

当过去时刻区间长度相同时，即TR为0.72 s且p=2、TR为1.44 s且p=1条件下，GCA均取决于过去1.44 s的区间；TR为0.72 s且p=3、TR为2.16 s且p=1条件下，GCA均取决于过去2.16 s的区间；TR为1.44 s且p=3、TR为2.16 s且p=2条件下，GCA均取决于过去4.32 s的区间；亦即较高时间分辨率数据检测出的显著EC条数总是远高于较低分辨率数据，提示当所利用的过去时刻区间相同时，时间分辨率越高，单位时间区间内数据所含信息越丰富，检测到的EC条数越多。

此外，相同模型阶数条件下，时间分辨率越高，单位时间区间内所含数据越丰富，过去时刻区间长度越短。因此，虽然过去时刻区间长度缩短并不一定总是使检测到的EC条数显著减少，但总体呈减少趋势。在此趋势影响下，随时间分辨率增高，检测到的显著EC条数仍然明显增多。综合以上结果，不论模型阶数如何，随着时间分辨率提高，检测到的显著EC条数均明显增多，提示将fMRI数据的时间分辨率提高至亚秒级可提高检测EC的敏感度。

WITT等[13]采用仿真fMRI时间序列数据比较结构方程建模、GCA和动态因果建模3种模型受TR的影响程度，发现结构方程建模对TR变化最不敏感而GCA最为敏感，提示从原始fMRI数据中能否正确推断出GCA因果关系在极大程度依赖于时间分辨率。LIN等[14-15]研究表明，虽然测量血氧水平依赖信号可反映神经元的血流动力学响应，但无法直接代表神经元发生的生理事件；这是由于病理条件可能导致某些大脑区域血流动力学响应发生变异，而提高采样率可显著提高脑区血流动力学响应与神经元活动的相关性，故高时间分辨率fMRI数据能更真实地反映神经活动[16]。数据采样率较低会使GCA结果在较大程度上受到血流动力学响应变化的影响，并偏离真实的神经元活动，即低时间分辨率数据的GCA结果在不同血流动力学响应下并不稳定，而高时间分辨率数据的GCA结果在血流动力学响应发生变化时仍保持稳定[7]，表明基于较高时间分辨率fMRI数据的GCA结果能更真实地反映脑区间神经元活动的因果关系。行GCA分析之前可通过采集同步电生理数据估计血流动力学响应情况，再针对去卷积后数据进行分析，但同步电生理-MR技术对受试者配合度要求较高，临床难以普遍开展；而通过提高时间分辨率以实现真实反映脑区间的因果关系更具现实及指导意义。

综上，提高fMRI数据时间分辨率可对GCA结果产生显著影响，高时间分辨率可显著提高GCA的敏感度，更加真实地反映不同脑区神经活动之间的因果关系。为得到更为稳定可靠的结果，欲行GCA分析时，建议以高时间分辨率采集fMRI数据。