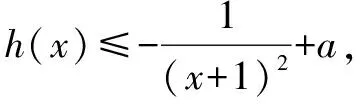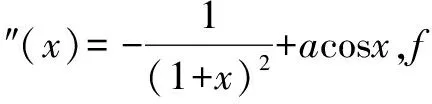基于数学直观的2021届武汉四月质检导数压轴题的求解

林新建

(福建省福清市教师进修学校 350300)

2021届武汉高三四月质检导数解答题以常见的对数函数、幂函数、三角函数为基本素材，以不等式恒成立问题为载体，考查各类数学思想和学生的综合能力.对于以指数、对数、三角函数为素材结合命制的含参导数试题，一般很难用常规的分离参数法求解，同时导数法也往往求解不出极值点，分类讨论及不等式放缩也较为繁琐.但是利用“直观”能够将问题中错综复杂的数据直观化和简明化，帮助我们冲破内隐条件的桎梏，直面问题的本质.

试题呈现已知函数f(x)=ln(1+x)-x+a(1-cosx).

(2)若存在正实数t，使得当x∈(-t,t)时，有xf(x)≥0恒成立，求a的值.

下面是参考答案给出的求解过程.

解析1 (1)略.

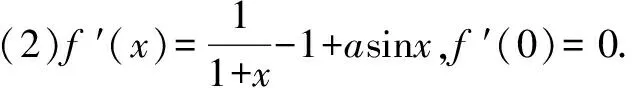
①当a=1时，h′(x)在(-1,1)上的单调递减，h′(1)=1-sin1>0.所以-10，所以h(x)单调递增.又此时h(0)=0，故-10，g(x)单调递增.所以-1f(0)=0， 此时存在t=1使得当-1

当x10，g(x)单调递增，所以x1f(0)=0，xf(x)<0，不存在t>0，使得当x∈(-t,0)时xf(x)≥0.

综上所述，a=1.

评析上述求解过程充分利用了f′(x)(即g(x))，f″(x)(即h(x))，f‴(x)(即h′(x))表达式的特征，通过对a的取值进行细分，以达到对这三个导函数的取值进行确定，从而最终实现对f(x)的增减性和符号的判定，构思巧妙.

解后反思求解本题后，笔者始终有种意犹未尽的感觉，于是重新审视了整个求解过程，并进行了一些思考.上述求解过程很巧妙，但其求解的整个思路并不是那么一目了然，是否存在更彰显试题本质的解法？因为试题最终是要判断函数y=xf(x)的符号，故可尝试从直观上加以理解，看能否从题设条件出发，预测出问题的求解思路.

直观分析①当x∈(-t,t)时，有xf(x)≥0成立，则x∈(-t,0)有f(x)≤0，且x∈(0,t)有f(x)≥0.因为f(0)=0，所以f(x)的图象过原点，要使得xf(x)≥0恒成立，直观判断f(x)的图象在x=0左侧附近及右侧附近均单调递增(得f′(x)≥0)；

③注意到f′(0)=0，f′(x)的图象过原点，要使得f′(x)≥0恒成立，直观判断f′(x)的图象在x=0左侧附近单调递减(得f″(x)≤0)，右侧附近单调递增(得f″(x)≥0)；

⑤由④得a=1.欲证a=1时xf(x)≥0成立，由于f″(0)=a-1=0，结合③中的分析，直观预测f″(x)图象在x=0附近单调递增，从而只需验证在x=0附近有f‴(x)≥0.

基于上述直观分析，笔者得到较参考答案更加简洁的求解过程.

解析2 (1)略.

①当a<1时，得f″(0)<0，则存在δ1>0，当x∈(-δ1,δ1)时有f″(x)<0，此时f′(x)单调递减.又f′(0)=0，则当x∈(0,δ1)有f′(x)<0，则f(x)在区间(0,δ1)内单调递减，f(x)0，使得当x∈(0,t)时xf(x)≥0.

②当a>1时，得f″(0)>0，则存在δ2>0，当x∈(-δ2,δ2)时有f″(x)>0，此时f′(x)单调递增.又f′(0)=0，则当x∈(-δ2,0)有f′(x)<0，所以f(x)在区间(-δ2,0)内单调递减，f(x)>f(0)=0，则xf(x)<0，不存在t>0，使得当x∈(-t,0)时xf(x)≥0.

③当a=1时，由于f‴(0)=2>0，则存在δ3>0，当x∈(-δ3,δ3)时有f‴(x)>0，所以f″(x)单调递增，结合f″(0)=0，得x∈(-δ3,0)时f″(x)<0，x∈(0,δ3)时f″(x)>0.从而f′(x)在(-δ3,0)内单调递减，在(0,δ3)内单调递增，且f′(0)=0，得x∈(-δ3,δ3)有f′(x)≥0，所以f(x)在区间(-δ3,δ3)内单调递增.由于f(0)=0，则x∈(-δ3,0)有f(x)<0，x∈(0,δ3)有f(x)>0，此时存在t=δ3使得当-δ3

综上所述，a=1.

上述求解过程与参考答案相比，更顺畅自然，一气呵成.无疑，这种顺畅自然、一气呵成来自于我们对题目所作的“直观理解”、解题方向的“直观判断”、最终结果的“直观预测”.在问题解决中，我们应努力寻求直观的手段和方法，努力实现“让问题在我们面前直观起来”！