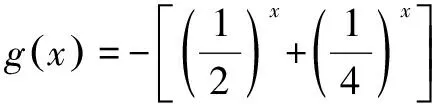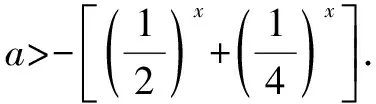恒成立问题的解题思路与常见解法

陈海东

(江苏省启东中学 226200)

一、借助一元二次函数的判别式解决恒成立问题

借助一元二次函数的判别式来解决恒成立问题的主要方式是，对于函数f(x)=ax2+bx+c，其中(x∈R)，若f(x)>0恒成立，那么此函数中一定有两个式子成立：a>0,Δ<0；若f(x)<0恒成立，那么a<0,Δ<0.当然，不同的题目有不同的要求，同学们要灵活处理.

例1若方程y=(m-1)x2+(m-1)x+2在x∈R上y>0恒成立，求m的取值范围.

解析因为当x∈R时y=(m-1)x2+(m-1)x+2>0恒成立.

所以根据函数的判别式可得：

联立上式可解得：1

所以m的取值范围为[1,9).

二、借助一次函数的性质解决恒成立问题

借助函数的性质来解决恒成立问题，主要指的是对于函数f(x)而言，如果函数f(x)>0恒成立，那么在x的区间范围内，当x为任意一个数值时，f(x)的值均大于零.例如：一次函数f(x)=kx+b，其中x∈[m,n]，若f(x)>0，那么f(m)>0，且f(n)>0.

例2已知|P|<2，且P∈R，若要使不等式(log2x)2+(P-2)log2x+1-P>0恒成立，求x的取值范围.

分析仔细观察这道题目，我们可以发现如果先解对数函数的不等式，得到p的取值范围之后，再去求x的取值范围，那么解题过程就会十分繁琐.因此，我们可以首先将对数不等式转化为关于p的一次不等式，然后在P∈(-2,2)的取值范围内，灵活使用关于p的一次函数的性质，得到两个关于x的不等式，然后求出x的取值范围.

解析因为|P|<2，且P∈R，即P∈(-2,2).

设f(P)=(log2x)2+(P-2)log2x+1-P，

因为不等式(log2x)2+(P-2)log2x+1-P>0恒成立，

三、借助函数的最值解决恒成立问题

在恒成立问题中利用函数的最值，其含义是在定义域内的两个函数f(x)和g(x)，如果f(x)≥g(x)恒成立，那么一定有f(x)max≥g(x)max，反之亦然.同样，如果a≥f(x)恒成立，那么一定有a≥f(x)max.我们在遇到恒成立问题时，可以灵活地运用函数的最值帮助我们求解.

解析若当x∈(-∞,1)时，f(x)恒有意义，

那么当x∈(-∞,1)时，1+2x+4x·a>0恒成立.

所以当x∈(-∞,1)时，g(x)为增函数.

除了以上提到的几点，还有其他关于恒成立问题的解法，如特值代入法等.虽然恒成立问题理解起来不是十分容易，但我们可以针对题目，具体问题具体分析，寻找合适的解法，因此，希望同学们及时归纳总结，并熟练掌握这些思路和方法.