高中数学中有关绝对值问题的解题策略

庞 萍

(宁夏银川市永宁县回民高级中学 753000)

一、利用零点分界，回避绝对值

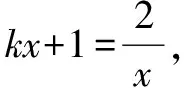
二、利用图象特征，回避绝对值

在课堂教学中，教师可以通过讲解的方式，引导学生利用函数的图象与y=f(x)图象的关系，对形如y=f(|x|)和y=|f(x)|的函数进行处理，将数学问题直接转化为与y=f(x)有关的函数问题，从而轻松找到解决问题的捷径.

例2 已知函数f(x)=|ex-bx|，其中e为自然对数的底，若函数y=f(x)有且只有一个零点，求实数b的取值范围.

解析因绝对值里面的函数比较复杂，所以通过找零点去绝对值无法顺利解决该问题.教师需要引导学生能够学会另一种解题思路，利用函数y=ex-bx与函数y=|ex-bx|图象的关系，问题就能够迎刃而解.

由于y=f(x)有且只有一个零点，即g(x)=ex-bx与x轴有且只有一个零点，即ex-bx=0有且只有一个解.

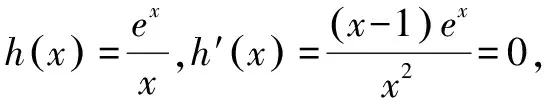
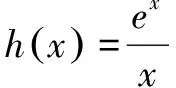
三、利用两边平方，回避绝对值

在有关绝对值问题的求解中，教师要引导学生去掉题中的绝对值符号，使得题目能够通过化简后进行分类讨论得出结果.而在去绝对值符号时，对于不等式的左右两边都是单项的绝对值不等式的情况下，将不等式两边同时平方，省去分析绝对值的意义，避免分类讨论的过程.

例3 存在不等式|x-9|≤|x-1|，求x的取值范围.

解析在本例题中，通常可以采用例2分类讨论的方法进行求解，但是过程较繁琐.仔细观察左右两边是单项的绝对值不等式，因此，可以直接平方化简不等式.

解析两边同时平方，得(x-9)2≤(x-1)2.

化简,得x2-18x+81≤x2-2x+1.

解得x≥5.

分析这是一个典型的左右两边都是单项的绝对值不等式的情况下进行平方的求解思路，在利用这个“平方”的时候，特别要注意“两边是单项的绝对值不等式”，如：|x+3|-|2x-1|≤x+1，存在复杂函数的过程中，不适用此方法.因此，在指导过程中要注意观察题干.

总而言之，在高中数学有关绝对值问题的教学中，教师们需要让学生们先有一个解题的思路，再对题目进行解决，使得他们能够在相对应的题型中“利用零点分界”“利用图象特征，回避绝对值”“利用分类讨论，回避绝对值”等解题方法对问题进行解决.从而帮助学生们提高在考试时的自信心，使得学生们能够取得优异的成绩.