基于Spark大数据计算模型的多种群并行进化遗传算法*

任 刚,吴长茂,魏 勇,刘小杰,郜广兰,王鲜芳

(1. 河南工学院 计算机学院,河南 新乡 453003; 2. 中国科学院软件研究所 并行软件实验室,北京 100190;3. 河南省生产制造物联大数据工程技术研究中心,河南 新乡 453003)

0 引言

遗传算法(Genetic Algorithm,GA)是一种借鉴生物自然选择机制的全局随机搜索算法,该算法通过选择、交叉和变异等遗传算子来搜索问题最优解。相较于传统搜索算法,该算法不需要专门领域的知识,仅用适应度评估函数来指导搜索过程,求解过程较为简单,同时最终结果不依赖于初始种群,具有较强的鲁棒性,从而在多个领域得到应用[1-3]。但是,由于传统GA中包含较多的遗传操作,当问题规模较大时,其性能降低,因此,通过并行方法来提高传统GA的性能成为该领域研究热点之一[4]。在众多并行遗传算法(Parallel Genetic Algorithm, PGA)中,基于MPI消息传递集群系统[5]的多种群并行进化PGA[6-8]被证明是一种有效提升PGA性能的机制。多种群并行进化PGA将整个种群平均分配到集群节点上,形成多个具有不同进化参数的并行进化子种群,并定期交换各自计算成果,从而提高了传统GA的收敛速度和计算效率,为用户提供了一套性价比较高的并行计算环境。

随着大数据时代的到来,以Spark为代表的计算模型由于其出色的数据并行能力被广泛应用。基于Spark计算模型的PGA (Spark-based Parallel Genetic Algorithm,SPGA)由于综合了Spark模型在数据并行上的优势和PGA在全局搜索上的优势,在多个领域受到欢迎[9]。然而,由于该算法缺乏多种群并行进化机制,当问题规模较大时,计算效率偏低。因此,急需将多种群并行进化机制引入经典SPGA中。由于消息传递集群的并行机制与Spark并行机制相差较大,现有的基于消息传递集群的多种群并行进化机制不适用于具有特定并行机制的Spark模型。为此,深入研究Spark模型的并行机制与多种群并行进化机制之间的关系,将多种群并行进化机制引入经典SPGA,以提高其收敛速度和计算效率,具体研究成果有:(1)将多种群并行进化机制引入经典SPGA,形成一种具有多种群并行进化功能的SPGA——多种群并行进化SPGA (Multi-population Parallel Evolutionary SPGA, MPE-SPGA);(2)将新算法应用到旅行商问题(Travelling Salesman Problem, TSP)上,通过3组实验验证该算法具有较高的计算效率。

1 相关工作

由于GA的遗传算子计算量较大,在解决大规模组合优化问题时,其计算性能往往成为该算法的瓶颈。因此,GA的并行化一直是该领域的研究热点之一。以Spark为代表的大数据并行计算模型由于其出色的数据并行能力而得到广泛应用。随之,基于大数据并行计算模型的PGA成为一个研究热点。Spark是一种基于内存计算的计算模型,较之传统的基于磁盘文件系统的MapReduce模型[10],更适宜像GA这类的迭代计算[9]。该模型在两次迭代之间,数据文件无需在磁盘上落地,可直接进入下次迭代计算过程,因此,节省了大量的磁盘I/O时间。因此,基于Spark计算模型的PGA成为一个新的研究热点。文献[11]提出了一种可以将适应度评估、交叉和变异等操作并行化的SPGA,并将此算法应用在测试案例生成问题中。文献[12]将SPGA引入传感器铺设问题,取得良好效果。文献[13]将SPGA应用到TSP问题中,结果说明SPGA具有较好的全局寻优性能。文献[14]将SPGA引入多峰函数极值问题,实验结果表明SPGA有较好的收敛性。可以看出,由于具有良好的性能,SPGA成为一种流行的基于大数据计算平台的PGA。但是,传统SPGA缺乏多种群并行进化机制,在问题规模较大的情况下,性能还不是太理想。因此,急需将多种群并行进化机制引入经典SPGA,以满足快速增长的计算需求。

2 多种群并行进化SPGA

2.1 Spark计算模型

Spark是一种以弹性分布式数据集(Resilient Distributed Dataset, RDD)为核心的并行计算模型,其并行架构如图1所示。RDD是基于内存的只读数据集合,通过转换(Transformation)和动作(Action)两类操作完成RDD处理。转换操作主要包括Map、flatMap和join等操作符。动作操作主要包括Reduce、count等操作符。较之传统的MapReduce模型,Spark操作符更丰富,有更强的表达能力。另外,基于RDD的编程方式效率更高。

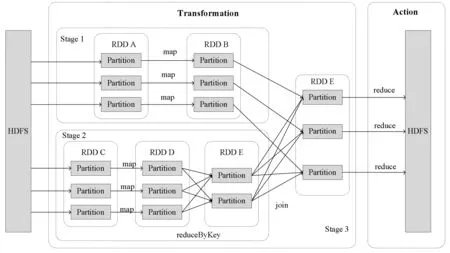
图1 Spark并行架构

2.2 遗传算法基本理论

GA是模仿生物进化理论而提出的一种优化计算模型,该算法通过模拟生物基因自然进化过程在全局问题空间里搜索近似最优解。整个解题过程如图3所示,包括种群初始化、评估、选择、交叉、变异等过程。该算法具有较强的鲁棒性。遗传算法面临的主要挑战是传个体数量与求解质量的关系。如果个体数量较少,整个种群收敛速度会很快,但是求解质量会很低。如果个体数量较多,其求解质量会升高,但是收敛速度会很慢。因此,在解决大规模数据样本的优化组合问题时,如何提高遗传算法性能成为关键因素。

2.3 多种群并行进化机制

多种群并行进化机制是提高传统GA性能的有效手段之一,其基本思想是用多个子种群代替原单一种群,每个子种群采用不同交叉概率Pc和变异概率Pm独立进化。在每代进化结束并生成新的种群后,找出所有子种群中的全局最优个体,将之重新分配到各子种群中,以促进各个子种群的进化。该机制可提高计算速度,避免单种群进化过程中出现的过早收敛现象

图1显示了一个基于消息传递集群的多种群并行进化遗传算法实例。该集群包含4个计算节点,其中3个节点分别对应子种群0,子种群1和子种群2,另外1个节点作为主节点。Sub-population0j表示子种群0的第j代个体,将该子种群的Pc和Pm设置为较大的值,用于在总的进化过程中不断探测新的解空间,因此,该子种群称为探测子种群。Sub-population1j表示子种群1的第j代个体,该子种群的Pc和Pm两值较小,称为开发子种群,用于在局部范围内寻找优秀个体,并将其保持下来;Sub-population2j的表示子种群2的第j代个体,其Pc和Pm两值处于中间,因此,该子种群兼具上述两个子种群的功能,称为探测开发子种群。在算法经过1次迭代后,各子种群首先搜索到本地最优解,然后发送到主节点,由主节点查找全局最优解,最后再发送回各子种群,形成下一代种群。可以看出,该算法通过具有不同进化参数的多个子种群的协作配合,完成全局寻优。

图2 多种群并行进化机制

2.4 多种群并行进化SPGA

图3显示了基于Spark模型的PGA实现总体架构。可以看出,经典SPGA一次迭代由Map和Reduce二个阶段构成。Map阶段多个集群节点同时启动多个Map任务,实现选择、交叉和变异这三个遗传算子,Reduce操作负责计算结果汇总和输出。Map操作1次处理输入数据文件的1行,每行包含多个遗传个体,这些遗传个体使用相同的交叉和变异概率进化。这实际上是一种单种群进化算法,其收敛速度和精度较之多种群并行进化算法来说,相对偏低。为了解决这个问题,将多种群并行进化机制引入经典SPGA,其关键点在于,本文将数据文件的1行看做1个子种群,每个子种群有多个遗传个体。每个子种群具有单独的交叉概率,种群个体形式化定义为:

图3 基于Spark模型的PGA架构

individual=〈code,fitness〉

(1)

其中,code为个体编码,fitness为个体适应度。多个individual个体构成1个子种群,这样,具有n个个体的子种群可形式化表示为式(2):

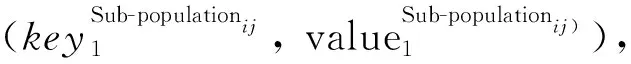
(3)

(4)

…,

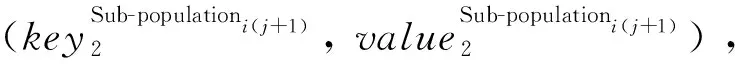
(5)

(6)

…,

该键值对被发送到Reduce,由Spark负责连接为(key2Sub-populationi(j+1), list(value2Sub-populationi(j+1)))。

Reduce负责汇总各子种群的所有个体,并找出全局最优解optimalIndividual,并将此解发送给各子种群。Reduce的输出键值对可表示为(key3Sub-populationi(j+1),value3Sub-populationi(j+1)),如式(7) (8)所示:

key3Sub-populationi(j+1)=Sub-populationi(j+1)

(7)

{optimalIndividual}—

{randomIndividual}

(8)

通过上述步骤,多个遗传个体形成若干个并行进化子种群,每个子种群都有不同的交叉概率和变异概率,并在进化过程中交换最优个体,共享计算成果。

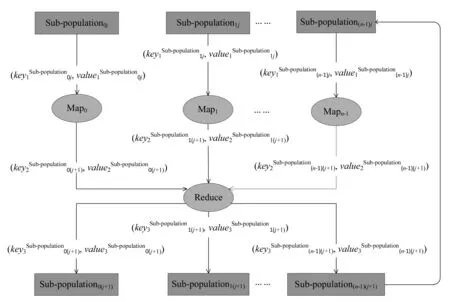
图4 基于Spark的多种群并行进化PGA实现

3 性能验证

3.1 集群主要参数

算法所用集群包含12个计算节点,主要参数如表1所示。

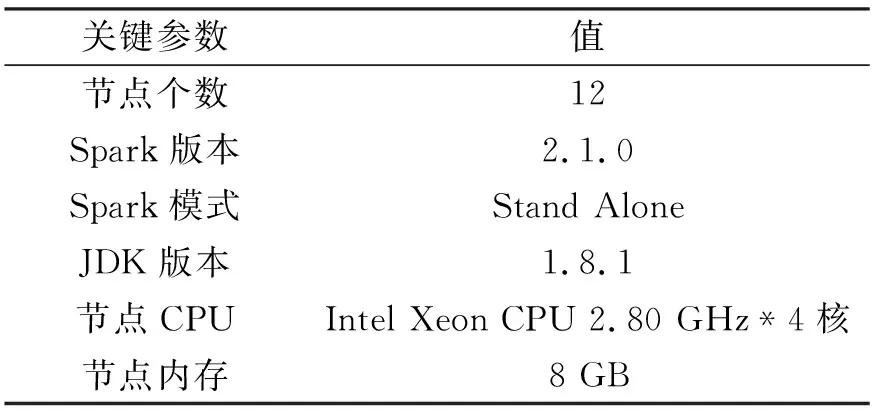
表1 集群主要参数

3.2 实验方案及结果分析

旅行商问题是典型的NP问题,随着问题规模的增加,其计算复杂度呈指数级增长,因此本文选取旅行商问题验证算法性能。采用TSPLIB库[15]中EIL51、CHl30和TSP225这3组数据集,它们分别代表小型、中型和大型3种问题规模。本文算法标记为MPE-SPGA,文献.[16]提出的算法记为SPGA。每个算法在3个数据集上运行20次,并记录平均运行时间及计算结果。

3.2.1 实验1:计算精度分析

计算节点数为3,每计算节点启动3个Map任务,每个Map任务分别对应开发、探测和探测开发3个子种群,共9个子种群。开发子种群的Pc和Pm为(0.3, 0.3),探测开发子种群的Pc和Pm为(0.6, 0.6),探测子种群的Pc和Pm为(0.9, 0.9)。最大迭代次数400,期望误差值4%。

结果展示在表2,可知两算法都能找到理论最优解,说明经过改造后的新算法寻优能力没有减弱。两算法平均解略有差异,采用双尾t-test双样本等方差假设检验[17, 18],自由度为138,显著度为0.05,比较两算法的平均解,其结果如表3所示。结果说明,这两种算法的平均解在统计学上无差异,证明改造后的算法在寻优能力上没有损失。

3.2.2 实验2:收敛速度分析

迭代次数取100,200,300,400,500,600,其他参数与实验1相同,其结果如表4所示。对于小问题规模EIL51数据集,两算法都能在100代以内达到收敛。对于中等问题规模CH130数据集,原算法在400代以内收敛,而本文算法在300代以内就能收敛。对于大问题规模,原算法在600代以内收敛,而本文算法在400代达到收敛。可以看出,随着数据集的增大,本文算法的优势越来越明显,说明本文算法在大问题规模数据集上有一定优势。

3.2.3 实验3:计算时间分析

计算节点数取2,4,6,8,10,12,最大迭代次数600,期望误差值4%,其他参数与实验1相同,其结果如表5所示。可以看出,对于各数据集,各计算节点数,本文算法的计算时间都要少于原算法,这说明经过改进的算法能够提高计算效率。

具体来说,对于EIL51数据集,随着计算节点的增加,计算时间反而增加。原算法的平均计算时间是50.35秒,本文算法平均计算时间为48.64秒,计算时间缩短了3%。这说明本文算法在小规模数据集上,优势并不明显。其原因在于,该数据集规模较少,运算量不大,大部分时间消耗在集群的通信和调度上。

对于CH130,两算法的计算时间都呈现先减少后增加的趋势,其原因在于当问题规模确定后,随着节点数的增加,并发度逐渐升高,计算时间会逐渐减小。但是,当节点数增加到一定规模,其节点间的通信和调度成本会逐步上升,超过节点增加带来的收益。原算法平均计算时间为103.39秒,本文算法平均计算时间为80.71秒,提高了22%左右。这说明本文算法在中规模数据集上有一定优势。

对于TSP225数据集,由于该问题规模非常大,所以随着计算节点逐步增加,两算法的计算时间都持续减小。原算法平均计算时间为167.12秒,本文算法的计算时间为114.84秒,计算时间提高了31%。

可见,本文算法对于大数据集具有特有的优势。可以预见,随着问题解空间的增大和计算复杂度的提升,运行时间随着节点数增加而减少的效果会逐步明显。

表2 计算结果对比

表3 双尾t-test检验结果

表4 收敛速度对比

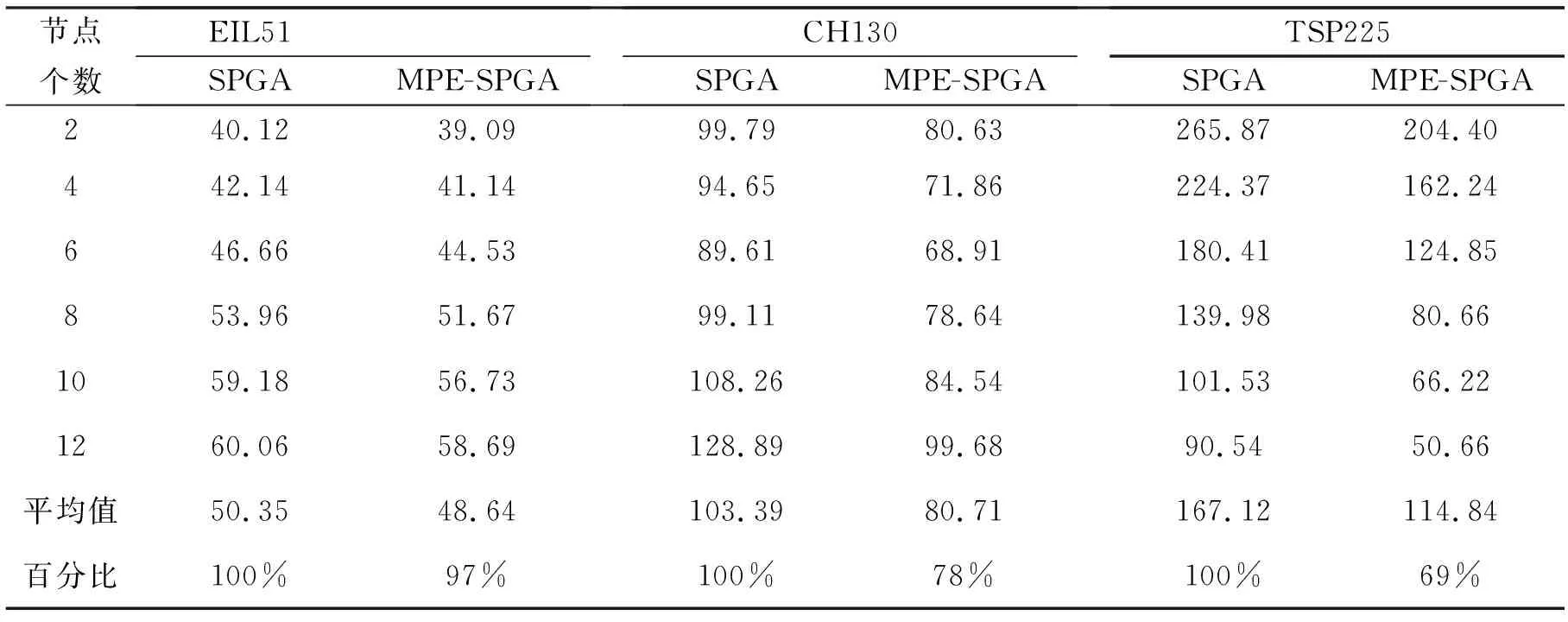
表5 运行时间对比

4 总结

将多种群并行进化机制引入经典SPGA,形成了一种新的SPGA——MPE-SPGA;将提出的方法应用在TSP上,并选择小型、中型和大型三种不同的TSP问题数据集进行试验,实验结果表明,提出的算法能够提高SPGA的收敛速度和计算效率。今后的工作是将该算法应用到相关领域解决具体问题。

(责任编辑 王 磊)