基于多维泰勒网的永磁同步电机调速系统非线性观测器*

翟海庆,崔瑞超,王彦昊,张 超

(1. 河南工学院 计算机科学与技术学院,河南 新乡 453003;2. 河南工学院 电气工程与自动化学院,河南 新乡 453003; 3. 西安热工研究院有限公司,陕西 西安 710054)

0 引言

在传统的永磁同步电机(PMSM)矢量控制系统中,速度传感器和位置传感器是不可或缺的。多数工业系统采用光电编码器或旋转变压器等机械传感器来检测电机速度和磁极位置,但在实际应用中,传感器的安装和更换都比较困难,维护和使用成本相对较高,难以达到调速系统简便、廉价、可靠等要求。因此,PMSM无传感器控制策略的研究受到国内外学者的广泛关注[1,2]。

常见的PMSM无传感器控制策略有:(1)模型参考自适应法[3]。使用该方法必须有一个准确的参考模型,否则其速度观察就会受到较大的影响,进而直接影响系统的速度辨识和调速系统的控制效果。(2)扩展卡尔曼滤波器法[4]。这种方法抑制噪声的效果较好,估计精确度较高,但如果电机参数发生变化,其估计精度就会受到较大的影响,而且该方法计算量很大,系统实时性难以满足。(3)磁通观测器速度估计法[5]。该方法的抗干扰性能较差,由于缺少误差校正环节,对电机参数变化特别敏感。(4)神经网络观测器法[6]。因受限于计算速度,该方法难以满足实时性的要求。

针对PMSM数学模型的非线性特性,首先应解决的是所设计观测器的稳定性问题。由于电动机存在参数/负载变化、外界干扰以及测量噪声,系统的速度估计和位置估计需要有自适应性。同时,理论分析和工程实践表明,多维泰勒网(Multi-dimensional Taylor Network, MTN)可以很好地取代传统的神经网络,完成对动态系统的建模和控制[7,8]。

综上所述,本文将MTN优越的逼近能力和自适应特性与观测器设计相结合,提出了一种基于MTN的PMSM系统非线性观测器设计方法,并设计了MTN的在线自适应学习规则,最后结合Lyapunov定理证明了非线性观测器的稳定性和有效性。

1 PMSM状态空间模型

为利于观测器估计,本部分首先将PMSM数学模型从d-q坐标系转换到α-β坐标系。

d-q坐标系与α-β坐标系的关系为:

(1)

其中iα和iβ分别为α,β轴定子电流;θ为转子位置。

α-β坐标系下的PMSM动态模型为:

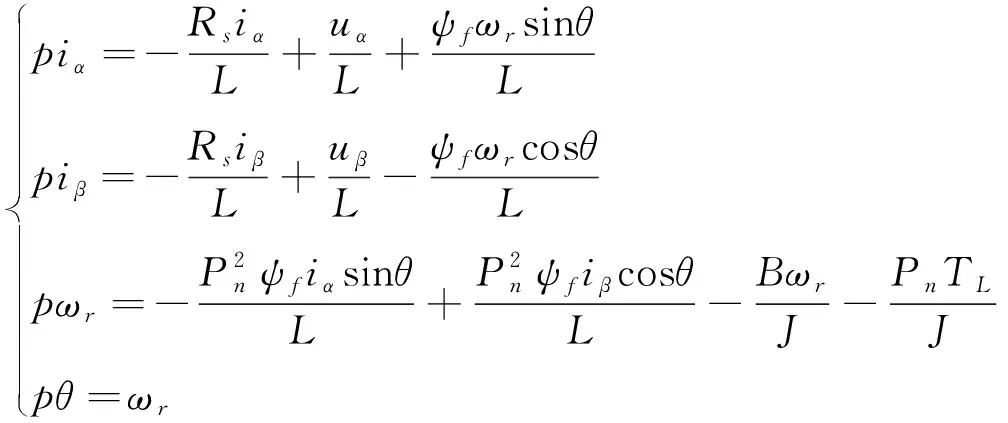
(2)

其中uα和uβ分别为α,β轴定子电压。

根据式(2),令

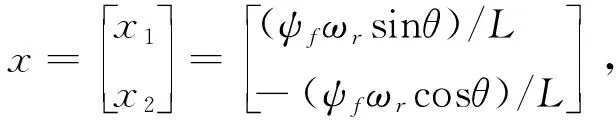
(3)

(4)

(5)

那么,式(2)可写成状态空间形式:

(6)

其中A∈R2×2,C=I∈R2×2是已知定常矩阵,矩阵对(A,C)可观测;系统输入u,v和输出y可直接测量。

用x来表示各变量,如果x可观测,则速度ωr和位置角θ分别为:

(7)

于是对ω和θ的测量就转变为对x的观测。

2 MTN观测器设计

MTN模型适合未知机理的一般非线性系统建模,如图1所示。基于多输入多输出的MTN模型,可以将n维非线性系统的动力学方程描述为:

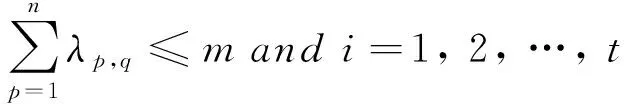
(8)

其中σi(·)表示非线性函数,用MTN模型描述,基本思路为用简单函数逼近复杂函数;wip是第p个变量乘积项之前的权值;N(n,m)是该展开式的总项数;λp,q是第p个变量乘积项中变量xq的幂次。

图1 多输入多输出MTN模型

由图1可见,MTN采用前向单中间层结构,只要N(n,m)足够大,就能以较小精度逼近任意模型[9]。表1比较了MTN和多层感知神经网络在一次迭代中的计算复杂度[10],突出了其结构简单所带来的较好的实时性能。此外,当n=3且m=1时,PID控制器是MTN的特殊形式[11]。因此,在电流环中经典的PID控制器可直接由只有一次项的MTN控制器代替。

表1 多层感知神经网络和MTN的计算复杂度比较

表中,nl表示MLP{n0,n1,…nL-1,nL}的第l层节点数,l=0,1…,L;n0和n1分别表示多层感知神经网络和MTN输入和输出层的节点数,而f(·)=tan(·)为神经节点的激活函数。

根据式(6),设计观测器为:

(9)

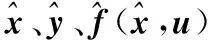
假设存在向量函数F(x,u),使得

f(x,u)=P-1CTF(x,u)

(10)

其中P为正定矩阵。

满足Lyapunov方程

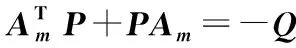
(11)

其中Q为正定矩阵。

根据MTN的逼近性质,式(10)中的连续向量函数F(x,u)可以用MTN来逼近。假设MTN的理想权值为w0,逼近误差向量为ε0,则

F(x,u)=w0g+ε0

(12)

其中ε0∈R2。

设w0有界,‖w0‖≤Mw,逼近误差也有界,‖ε0‖≤εsup。

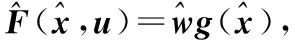
(13)

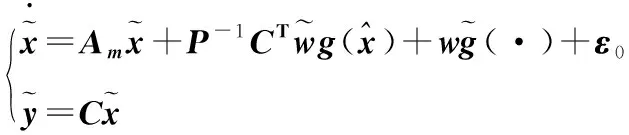
(14)

3 MTN观测器稳定性分析

本部分将从理论的角度来论证MTN网络观测器的稳定性,结合Lyapunov稳定性理论,可设计MTN网络权值的学习规则为:

(15)

其中Γ为控制收敛速度的正常数,δ为设计的修正参数。

令Lyapunov函数:

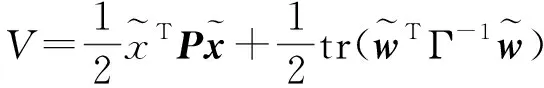
(16)

则

(17)

其中

(18)

(19)

则

(20)

又因

(21)

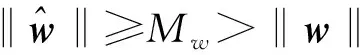
所以

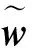
4 算例分析

本部分将MTN自适应观测器用于改进文献[12]的PMSM调速系统,并进行算例分析以验证所设计非线性观测器的有效性。改进后的仿真系统如图2所示,其中速度环控制为MTN逆控制方法,电流环控制器为经典PI控制器。速度设定为100rad/min。PMSM参数如表2所示,电机参数与文献[12]一致。

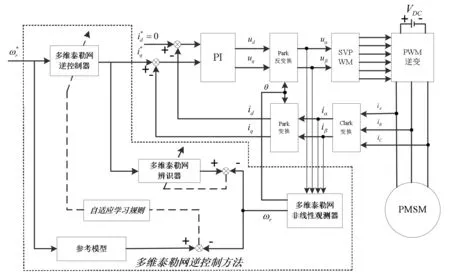
图2 基于非线性观测器的PMSM多维泰勒网逆控制调速系统

表2 PMSM参数

PMSM调速系统在预设参数时,观测器估计结果如图3和图4所示。改变参数后,J增大10倍,观测器估计结果如图5和图6所示。从系统仿真的结果可以看出,本文所提出的MTN观测器对PMSM系统的参数估计精度较高,经较短的暂态过程后,可很快收敛到真实值,且对电机参数变化和外界干扰的鲁棒性较强。

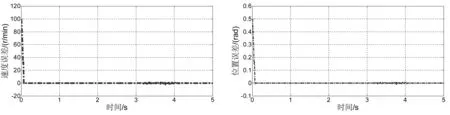
图3 预设参数时MTN观测器速度估计误差 图4 预设参数时MTN观测器位置估计误差

图5 改变参数后MTN观测器速度估计误差 图6 改变参数后MTN观测器位置估计误差

5 结束语

针对PMSM调速系统,提出一种基于MTN的非线性观测器方法。结合Lyapunov稳定性定理,设计了MTN权值的在线学习规则,证明了基于MTN状态观测器的稳定性。仿真结果表明,MTN观测器对PMSM调速系统的估计精度高,具有较强的鲁棒性和令人满意的实时性能。