基于混沌电路的压电谐振器动力学特性研究*
赵向阳,周慧琳,王 磊
(1.河南工学院 车辆与交通工程学院,河南 新乡 453003;2.河南工学院 材料科学与工程学院,河南 新乡 453003;3.河南工学院 经济学院,河南 新乡 453003)
0 引言
混沌是在确定性系统中发生的貌似随机的无规则或不规则运动[1]。混沌是系统固有的特性,它的表现是复杂的,既非准周期和周期运动,又非随机运动,而是呈现出对初值敏感的貌似随机现象[2-3]。从20世纪70年代以来,混沌研究取得了较大进展,在数学、物理学、生物学、生态学、气象学、通信、医学等诸多领域得到了广泛应用并取得了可喜的成绩[4-6]。
1 非线性电路中的混沌演化过程
混沌是非线性系统在特定条件下的一种非线性动力学行为,已有大量研究表明在一些非线性电路中存在混沌现象[7]。比较典型的混沌电路有Chua电路、Chen电路、Jerk电路、Lorenz电路和L?电路等。其实,从混沌发现以来,通向混沌的途径一直是非线性系统的重点研究方向[8]。目前,通向混沌的主要途径有:概周期分叉、阵发性、倍周期分叉、激变、擦边分叉[9-12]。
以林森电路为例分析混沌的演化过程。林森电路构成如图1所示,其中线性电感L=100μH,线性电阻R=200Ω,D是一变容二极管,u是一正弦交流电压(频率2MHz)。
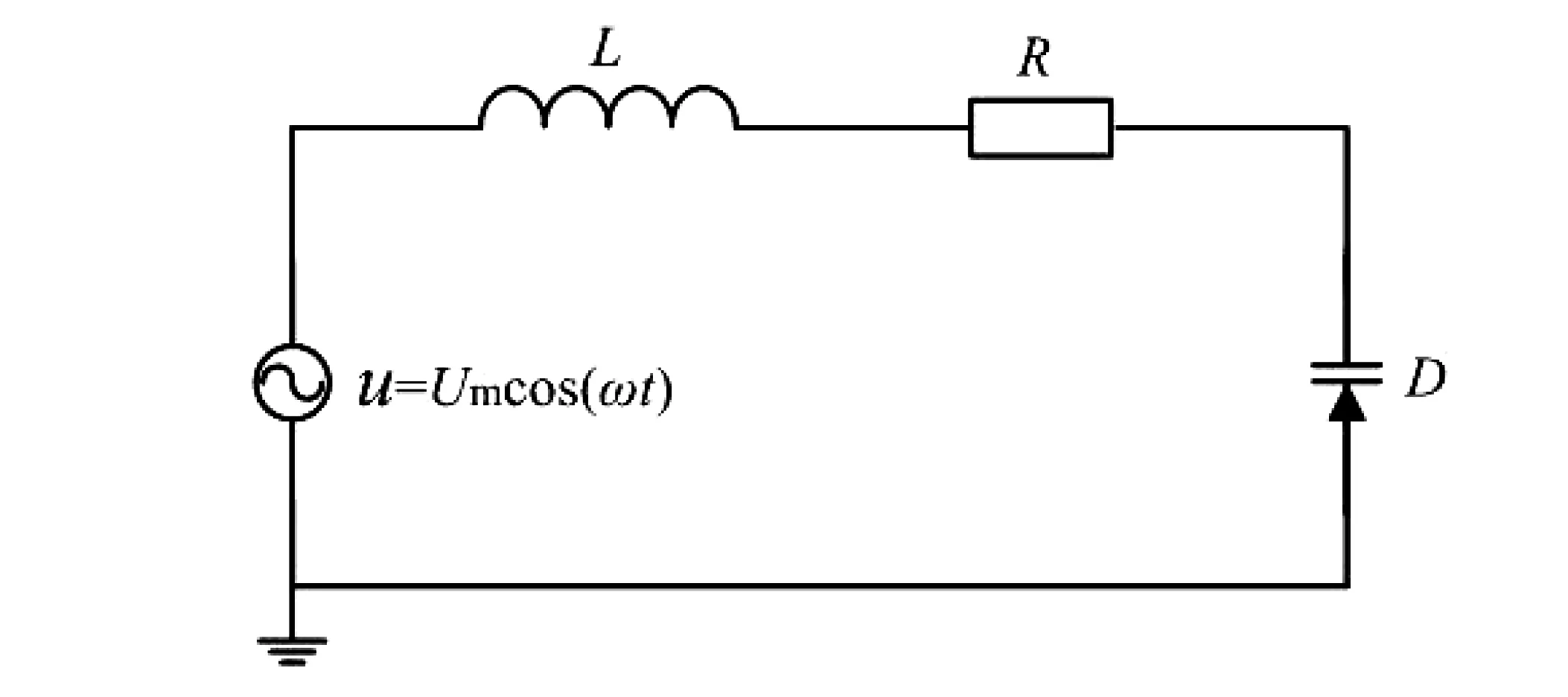
图1 林森电路原理图
如图2所示,电压幅值Um变化引起电流的复杂变化。当Um<1V,即图2中0~Um1段,电路中电流I是一周期非正弦电流,其频率、周期和u相同。当Um1 图2 回路电流I随Um变化情况 压电谐振器是谐振式传感器和执行器的核心部件,通常工作在共振和稳幅状态。在外部简谐振动激励作用下,压电谐振器可以等效为一正弦交流电源和一电容串联。将其与电阻、电感和非线性电容串联,设计的电路如图3所示。 图3 压电谐振器分流电路 其中,Cp是压电谐振器固有电容;非线性电容Cn有以下库伏特性: vc=aq3 (1) 其中,vc和q分别是非线性电容两端电压和电荷,a是非线性系数。 对图3所示电路,根据基尔霍夫定律,有 (2) 很显然,这是一个Holmes型Duffing方程。 对方程(2)进行等效变换: (3) 方程组(3)是典型的一阶微分方程组,很难求其解析解。利用四阶龙格库塔算法求其数值解。将方程组(3)继续进行变换,令 (4) (5) 其中,x是向量,F(x,t)是向量函数。方程组(3)可以变换为如下形式: (6) 方程(6)可由以下方程进行迭代求解: (7) 其中, l1=F(xn,tn) (8) (9) (10) l4=F(xn+Δtl3,tn+Δt) (11) 方程(7)给定一个初值,利用MATLAB编制程序即可求解。 给定参数L=1H,R=0.1Ω,Cp=1F,a=1,ω=1rad/s,给定初值q=0,i=0,对等效电路系统方程进行求解,得出电路输出信号随时间变化的时域波形图和相图。图4、图5、图6分别是其他参数不变情况下仅改变激励电压Vm值时系统输出的结果。 (a)电荷时域波形 (b)电流时域波形 (c)相图图4 Vm=0.1,初值q=0,i=0时电路输出结果 由图4—6可知,随着激励电压幅值的增大,系统特性发生变化,电路输出波形从简单到复杂,但并没有很强的规律性,这证实了确定电路中的不确定性,即貌似随机性的行为特征。且从图6可以看出,该系统的轨线满足不交率,即两条最大轨线不可能穿过同一常点,因为其解的光滑映射是唯一的,所以其轨线在相空间只能缠绕而不会相交,这时系统出现混沌现象。 (a)电荷时域波形 (b)电流时域波形 (c)相图图5 Vm=10,初值q=0,i=0时电路输出结果 (a)电荷时域波形 (b)电流时域波形 (c)相图图6 Vm=90,初值q=0,i=0时电路输出结果 本文通过将压电谐振器等效并串联非线性电容构建了一个典型的受迫Duffing电路,同时建立了其动力学方程,并着重研究了 Duffing 电路的非线性动力学特性。通过将Duffing 方程降阶并编制程序进行数值仿真,系统表现出了复杂的动力学行为;在选择适当的电路参数时,系统进入混沌状态。对于Duffing 电路,其非线性特性在各种领域有着极大的潜在应用价值,如将其初值的敏感特性应用在保密通讯中,在其随机共振响应下可以进行信号检测等。这项研究有着重大的理论和工程应用价值[12]。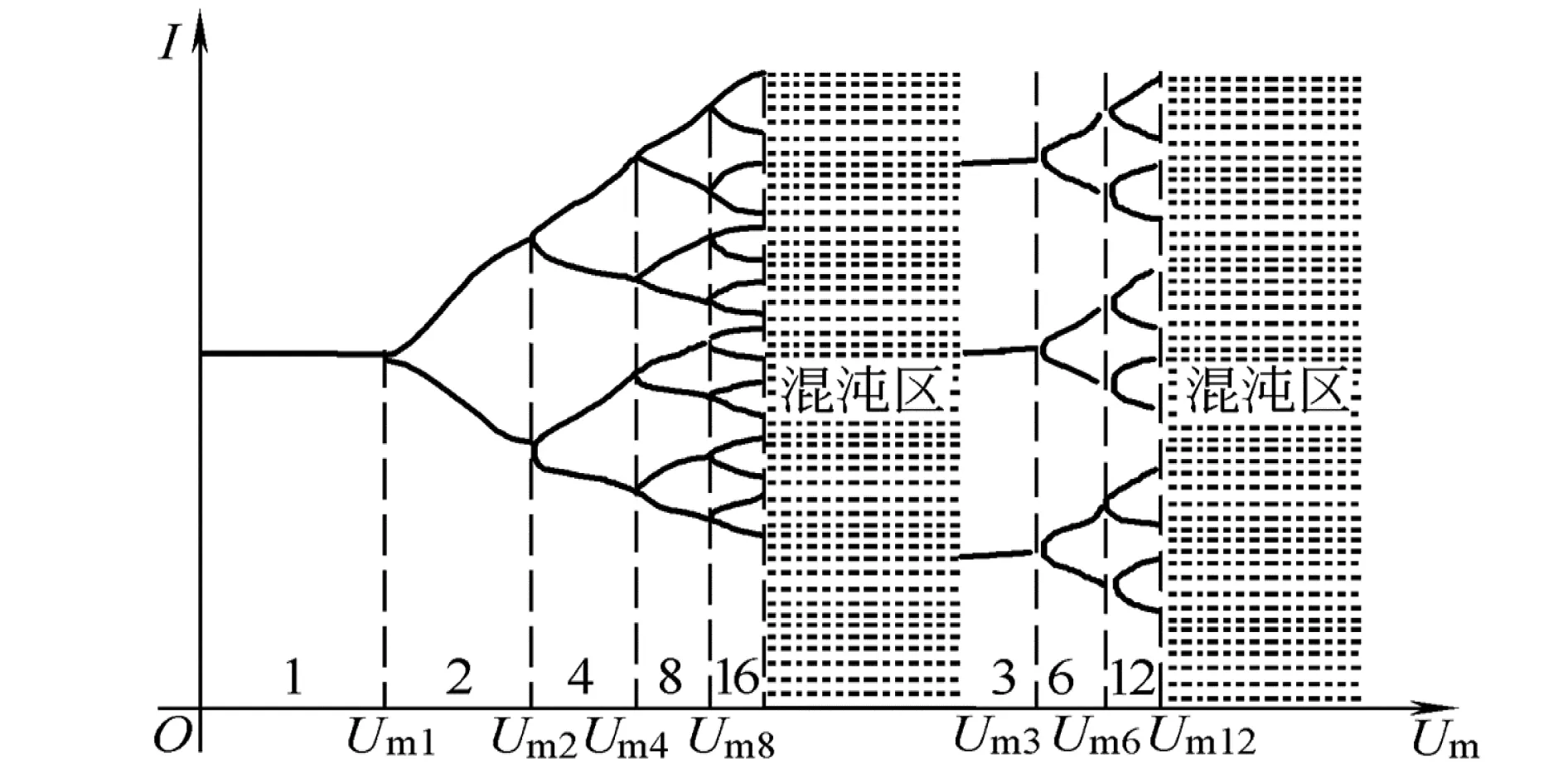
2 压电谐振中的混沌现象
2.1 等效电路
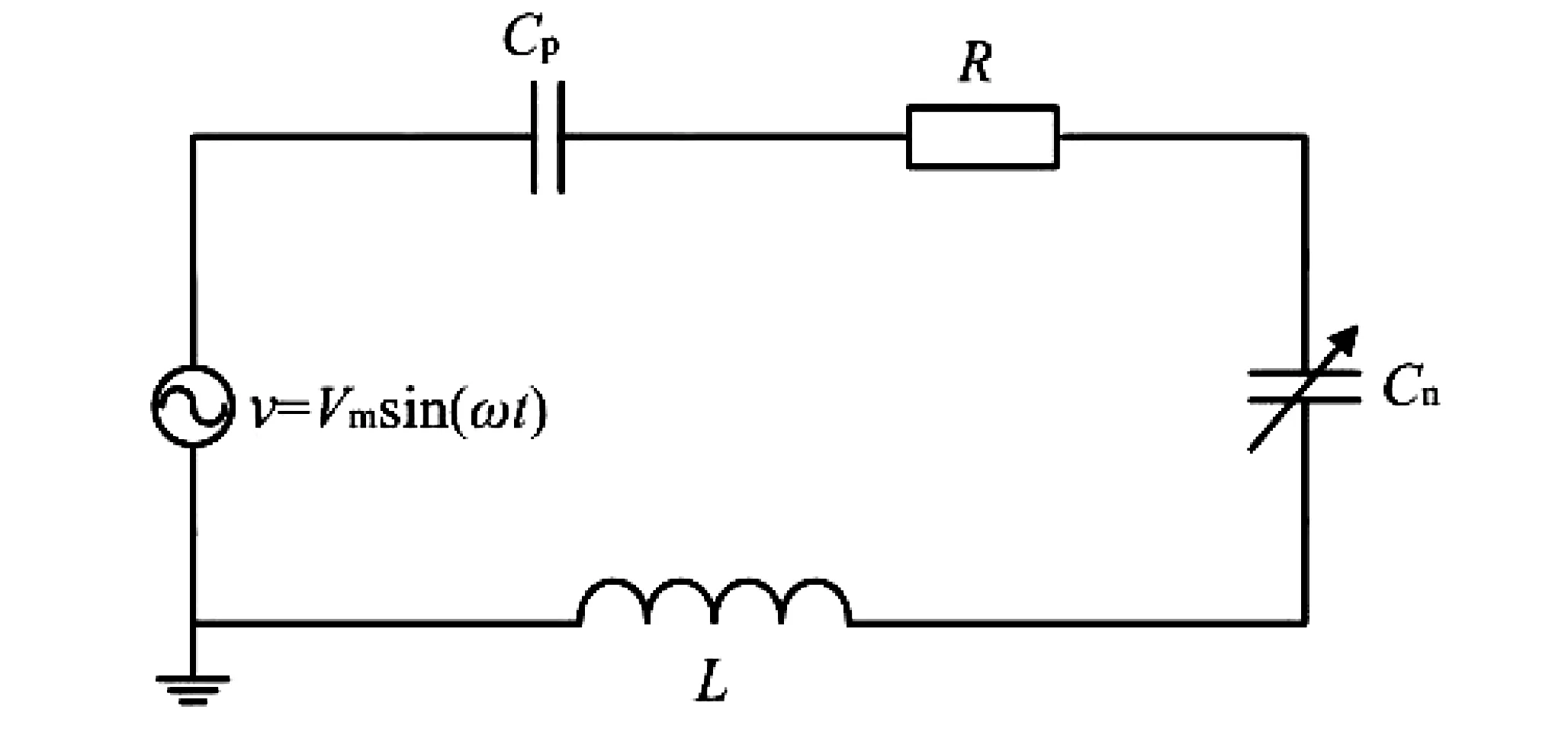
2.2 等效电路求解方法
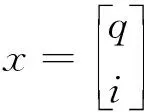
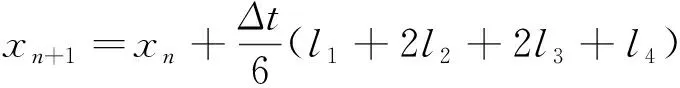

2.3 等效电路中的混沌现象
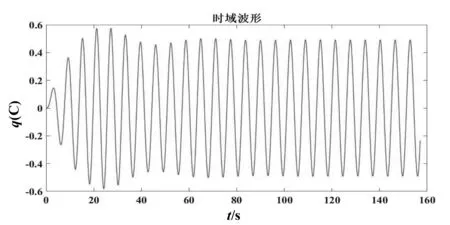

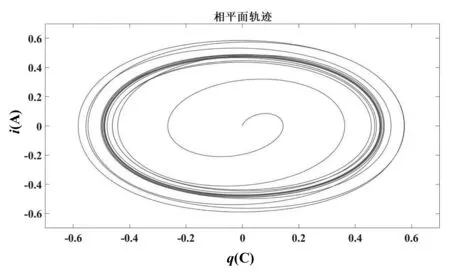
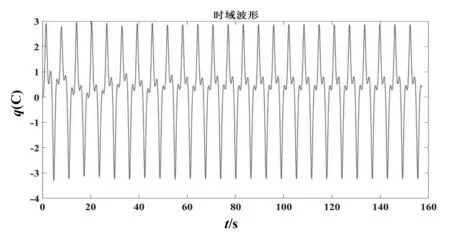


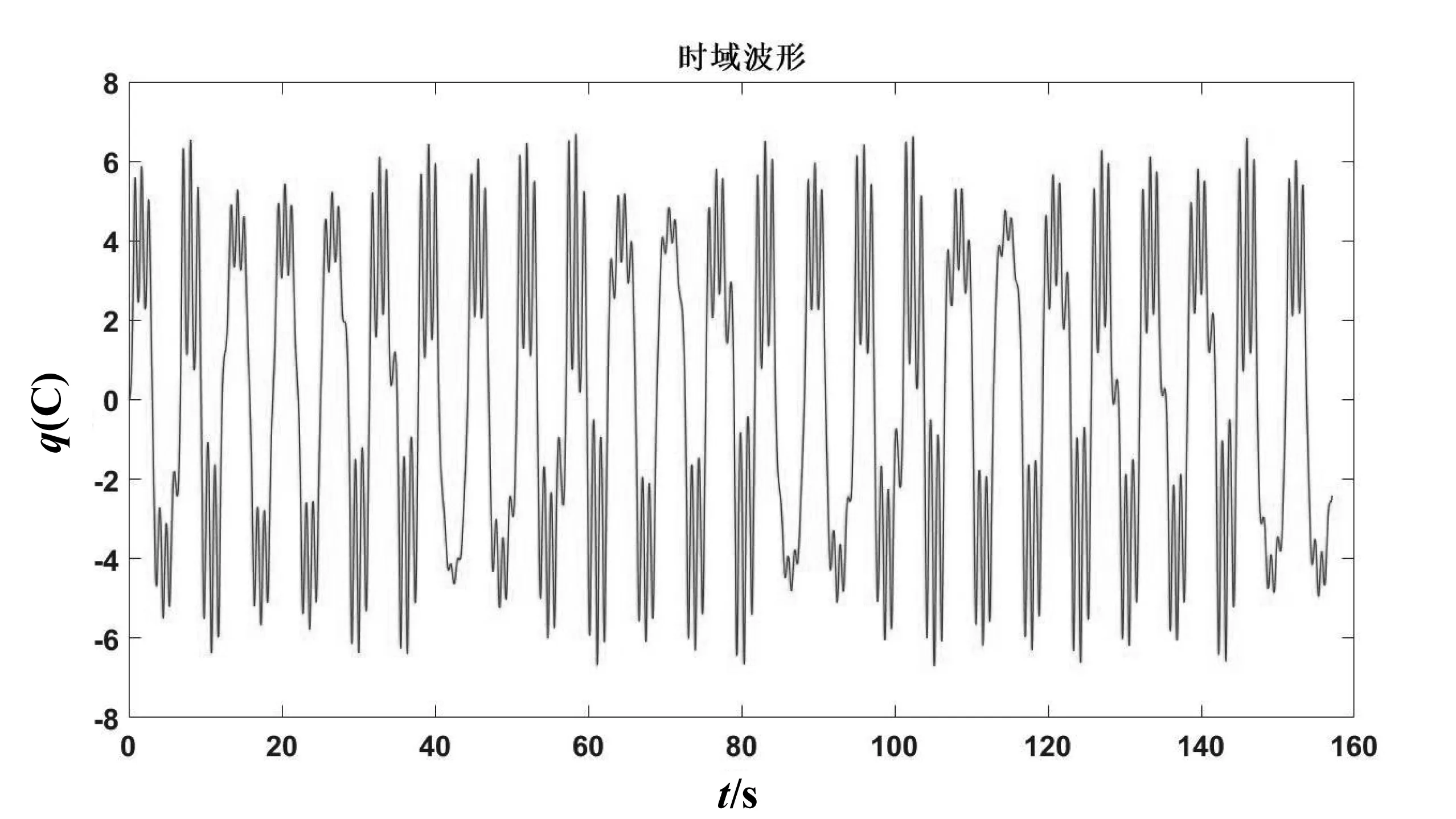

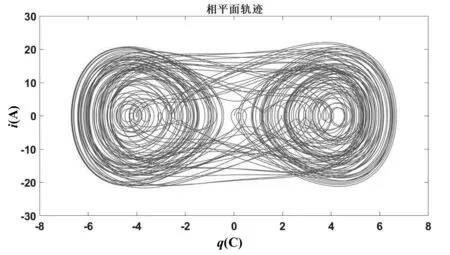
3 结论

