基于改进神经网络PID的永磁同步电机控制研究

闫浩安，李建冬

(北京机械设备研究所，北京 100854)

0 引言

永磁同步电机(permanent magnet synchronous motor，PMSM)是一种结构简单，高效实用的电机，具有转动惯量小、无需励磁绕组、功率密度高等优点，在要求快速响应、宽调速范围、高精度控制的应用场合中的应用日益广泛[1-2]。

由于PMSM是一个高度耦合的时变非线性系统，其定子电阻、交直轴电感在运行中随温度、磁路饱和等效应而变化，而传统的控制方法皆是假设时变参数为常值，达到一种近似精确的控制。而为了真正发挥电机的各种优点，则需要寻找到一种控制方案对假设条件有更好的拟合[3]。

随着近年来智能优化算法的进步以及计算机算力的提升，各种智能算法以其对非线性问题的高效求解能力，被逐渐应用到电力调速领域。针对内置式永磁同步电机(internal permanent magnet synchronous motor，IPMSM)常采用最大转矩电流比(most torque per ampere,MTPA)控制策略，充分利用其凸极效应产生的磁阻转矩达到最大的输出力矩[4-5]。

本文针对IPMSM,在传统MTPA的基础上，采用差分进化算法(differential evolution algorithm,DE)优化的神经网络比例积分微分(proportion integration differentiation,PID)控制，使用DE对小规模神经网络进行优化迭代，寻找到适合特定电机的神经网络参数，使其能够在电机运行中输出适合实时状态的电流环PID参数，仿真实验证明这种PID参数整定方法可以有效改善电机的控制特性。

1 控制系统模型

1.1 永磁同步电机的数学模型

近年来,业界在IPMSM的控制策略上，往往采用最大转矩电流比(MTPA)控制，其主要思想为通过调整电流矢量方向，使最小的电流值产生最大的电磁转矩，从而实现对电机的高效率调速控制[6]。

为了对电机控制模型进行数学描述，将电机模型进行适当的简化[11]，作如下假设：

(1)电机中的电流为完全三相对称的正弦波，无空间谐波；

(2)忽略电机铁芯的磁路饱和以及电机中的涡流和磁滞损耗。

在同步旋转d-q坐标系下建立数学模型：

电机的电压方程：

(1)

电机的转矩方程：

(2)

电机的运动方程：

(3)

式中：ud,uq为dq轴等效电压;id，iq为dq轴等效电流；R为定子电阻；Ld，Lq为直轴和交轴的等效电感；ωe为电角度转速；ωr为机械角度转速；Te为电磁转矩；TL为负载转矩；ψf为永磁体磁链；J为电机转动惯量；B为阻尼系数；p为极对数。

最大转矩电流比控制的原理即通过最小的is得到最大的Te的控制方法[8-9]，其表达式为

(4)

式中：is为电流有效值。

1.2 控制系统模型

图1为通过差分进化算法优化神经网络PID的系统框图。包含4个部分：①差分进化算法模块，外环迭代对神经网络参数进行调整；②神经网络模块，根据电机运行状态，实时整定电流环PI参数；③传统PID模块；④电机模块以及空间矢量脉宽调制(space vector pulse width modulation,SVPWM)模块。

图1 差分进化算法优化神经网络PID的PMSM系统框图Fig.1 System diagram of PMSM servo system using neural net PID optimized by DE

2 控制算法

PID控制理论成熟完备，各行业的线性控制系统中应用广泛，而在高度耦合的时变非线性系统中则不能说尽如人意[10-11]。神经网络有着很强的拟合能力，理论上能以任意精度拟合任意线性或非线性连续函数，故将神经网络与PID结合起来，应是非线性系统的有效控制方法[12]。

2.1 差分进化算法

差分进化(differential evolution,DE)算法是一种出色的全局优化算法，被证明在全部进化算法中具有最高的效率。将神经网络的全体权值和偏置作为DE的求解目标，对神经网络参数进行寻优，可以快速得到较优解，且不易落入局部最优[13-14]。

DE算法的含义为，首先生成解的种群，逐一对其中的个体与种群中另外2个体的差值相加，再计算适应度后，按照适者生存进行选择，反复迭代搜索最优解。个体的适应度函数(也即网络的损失函数)采用误差绝对值时间积分IAE，即

(5)

编码方式采用实数编码。变异策略采用DE常用策略中的DE/best/1：

vi,g=xbest,g+F(xr1,g-xr2,g),

(6)

式中：vi,g代表第g代种群中第i个个体所发生的变异;xbest,g代表第g代种群中具有最佳适应度的个体;xr1,g,xr2,g代表种群中第r1,r2个不同的个体;F为缩放因子，其取值范围为[0,2]。变异进行交叉操作，采用二项式交叉：

(7)

式中：ui,g代表第g代种群中第i个个体的进行交叉之后的结果；CR表示发生交叉的概率。之后根据贪婪策略，选择适应度更优的个体加入到下一代种群中，进而重复这个迭代的过程，直到达到最大迭代次数。

2.2 神经网络PID控制算法

随着近年来计算机算力的提升，具有强大拟合能力的神经网络重新变为研究的热点。每个神经元具有多个输入项和对应数量的权值和一个常值偏置，以及一个非线性激活函数以避免网络输出等同于线性多项式，而神经网络由多层多个神经元组成。

本文算法中神经网络的输入层设置6个输入项，分别为电机的转速信号及其积分、q轴电流及其积分、d轴电流及其积分，激活函数采用反正切函数，取其有界性和原点对称性，神经网络的2个输出对应了电机伺服回路中电流环的2个PID控制器的参数。

鉴于PMSM运行中信号噪音较大，微分控制则会引起较大的信号振荡，所以通常采用PI控制器。神经网络输出的目标正是PI控制器的控制参数，而DE算法优化的直接目标为神经网络的权值。

2.3 优化PID算法步骤

差分进化算法的具体流程步骤如图2所示。

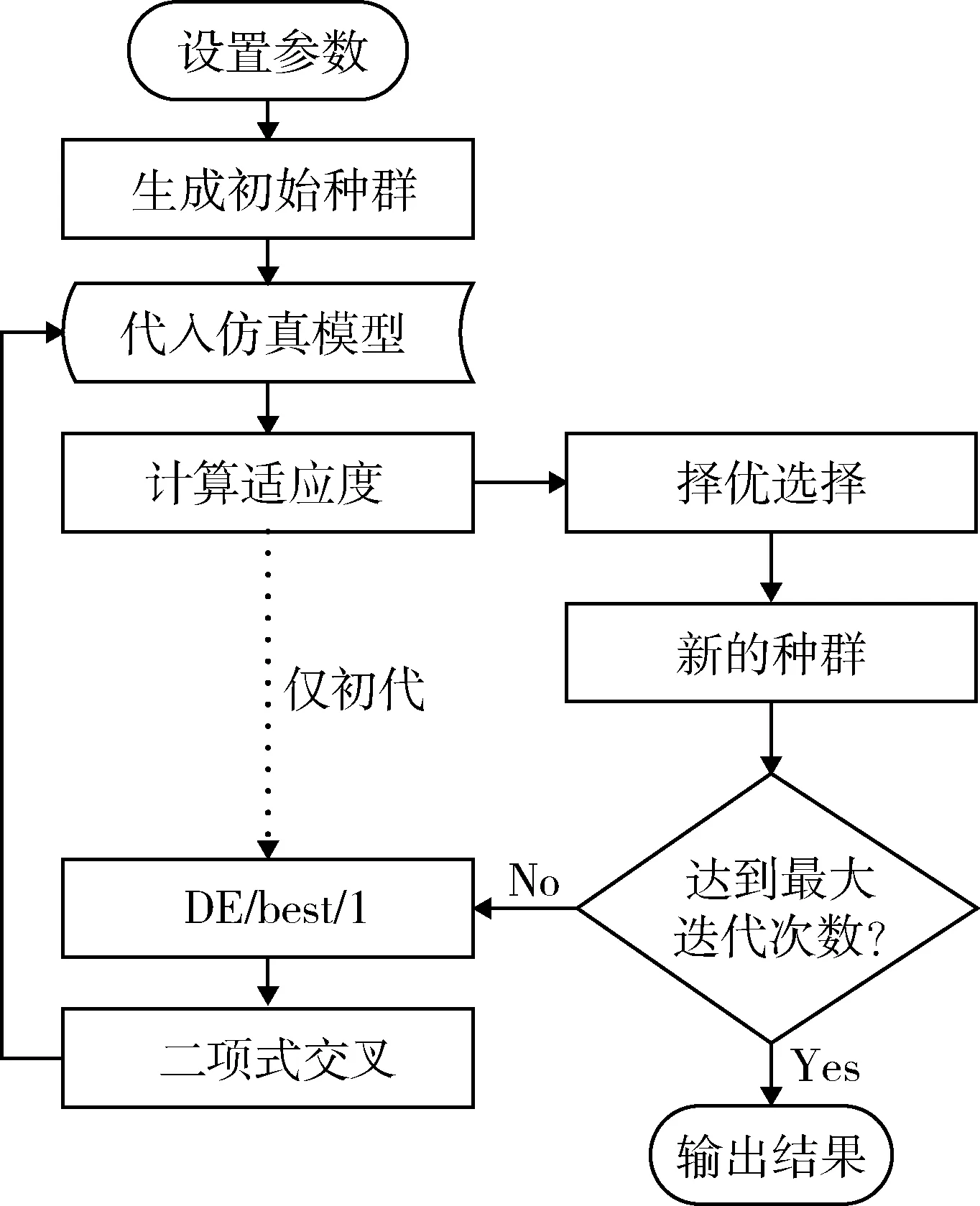
图2 差分进化算法流程图Fig.2 Flow chart of differential evolution algorithm

步骤1：初始化阶段。设置差分进化算法的种群规模为，迭代次数G，缩放系数F；神经网络的隐含层H个神经元。随机生成P个可以输出接近传统PI参数值的网络，逐个带入仿真模型，计算初始种群每个个体的适应度，作为迭代计算的起点。

步骤2：变异与交叉阶段。按照前文所述差分计算算法的变异、交叉操作，对种群中每个个体进行操作，并将操作后的个体带入仿真模型计算适应度。

步骤3：产生新种群阶段。依据适应度对种群进行选择操作，产生新的个体。

步骤4：若未达到最大迭代次数G，则重复步骤2～3；若达到G次，运算结束。

3 永磁同步电机的系统仿真实验

3.1 仿真实验模型建立

本系统仿真实验的仿真对象为内置式正弦波永磁同步电机(IPMSM)，矢量控制方法采用MTPA控制，仿真在电机的基速范围内进行。系统仿真模型如图3所示。

图3 差分进化算法优化神经网络PID的PMSM仿真模型Fig.3 Simulation model of PMSM servo system using neural net PID optimized by DE

模型主要的模块有DE-神经网络PID调节器、电流环PI控制器、转速环PI控制器、SVPWM模块[15]、IPMSM模块。其中电流环PI控制器参数由差分进化算法进行整定，使用虚线部分表示。

3.2 仿真结果分析

电机的参数设置如表1所示。

表1 电机参数表Table 1 Motor’s parameters

为了保证训练的有效性，设置仿真条件如下：仿真时间0.2 s，初始速度指令和负载都为0，在0.02 s 施加第1个阶跃速度指令，在0.06 s和0.08 s再次施加2个一正一负的方波指令，0.14 s施加40 N 的负载，差分进化算法种群规模20，迭代30次。从Simulink的仿真中输出传统PID的控制曲线和本文中的优化方法的控制曲线(图4)和整个迭代过程中的适应度收敛过程(图5)。

图5 差分进化算法优化过程适应度收敛曲线Fig.5 Fitness convergence curve during DE optimizing

图4中可以看出，本文提出的算法相比传统PID可以使稳定时间提前到来，且显著降低静差，挂加负载后也可以更快地消除负载所带来的干扰，有效提高电机响应的跟随特性，提高了抗干扰能力。从图6可以看出，整个迭代过程保持有效的收敛速度，种群规模不太大的设定之下，无需非常大的迭代次数即可获得有效的收敛优化效果。

图4 算法优化结果的电机运行仿真对比图Fig.4 Comparison diagram of motor running simulation as a result of algorithm optimization

为验证算法优化出的网络可以在多种输入信号下都可以保持较好的性能，设计如下实验进行验证。在系统的转速指令输入端施加10～80 Hz的正弦波形(图7中以20 Hz为例的速度响应曲线)，每0.2 Hz测量转速误差的幅值和相位，以此来反映系统转速的幅频响应和相频响应，进而体现出系统对多种信号的跟随性。

从图6可见，对于代表低变化率信号的低频指令，本文算法优化的系统能以更低的幅值衰减跟随指令信号；从图8可见，对于中高变化率的指令信号，本文算法优化的系统具有更低的相位延迟，说明具有更短的上升时间，也即更好的时域响应，验证了算法对于多种输入具有一定的鲁棒性。

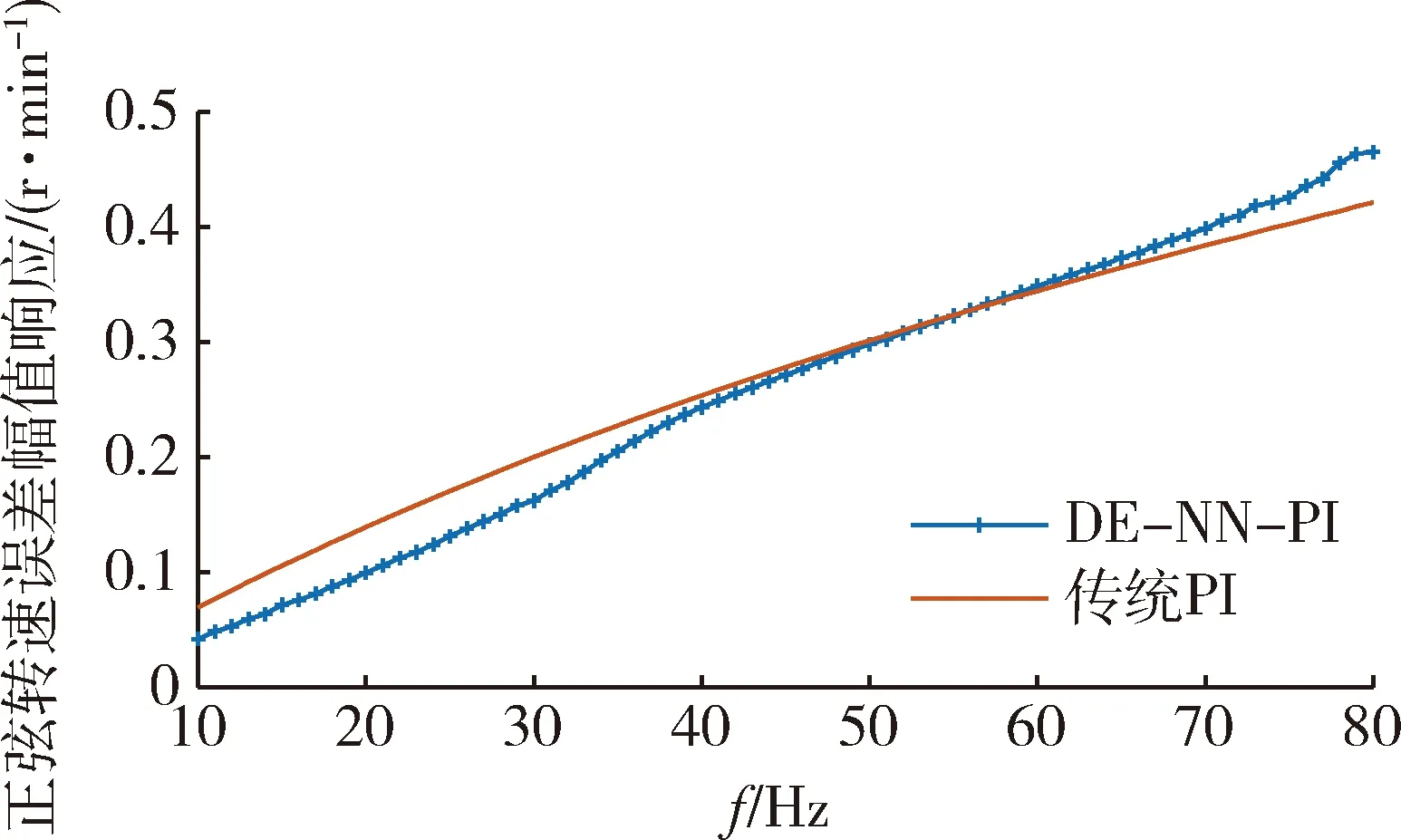
图6 系统转速误差的幅频响应Fig.6 Magnitude-frequency response of rotate speed error

图8 系统转速误差的相频响应Fig.8 Phase-frequency response of rotate speed error

4 结束语

差分进化算法具有全局搜索能力，可提高网络的学习效率，加速全局收敛;神经网络具有自学习的任意逼近能力。本文将差分进化算法、神经网络与传统PID相结合，应用于内置式永磁同步电机的MTPA控制中。仿真结果表明，该控制区具有良好的控制精度和动态调节品质。